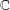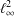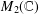In this paper, we give a complete description of left symmetric points for Birkhoff orthogonality in the preduals of von Neumann algebras. As a consequence, except for $\mathbb{C}$, $\ell _{\infty }^{2}$ and $M_{2}(\mathbb{C})$, there are no von Neumann algebras whose preduals have nonzero left symmetric points for Birkhoff orthogonality.

In this paper we study a Haagerup inequality in the general case of discrete groupoids. We develop two geometrical tools, pinching and tetrahedral change of faces, based on deformation of triangles, to prove it. We show how to use these tools to find all the already known results just by manipulating triangles. We use these tools for groups acting freely and by isometries on the set of vertices of any affine building and give a first reduction of this inequality to its verification on some special triangles and prove the inequality when the building is of type $\tilde{A}_{k_1}\times\cdots\times\tilde{A}_{k_n}$, where $k_i\in\{1,2\}$, $i=1,\dots,n$.