Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T20:54:22.763Z Has data issue: false hasContentIssue false
  • English
  • Français

LEFT SYMMETRIC POINTS FOR BIRKHOFF ORTHOGONALITY IN THE PREDUALS OF VON NEUMANN ALGEBRAS

Part of: Normed linear spaces and Banach spaces; Banach lattices Selfadjoint operator algebras

Published online by Cambridge University Press:  28 August 2018

NAOTO KOMURO ,
KICHI-SUKE SAITO  and
RYOTARO TANAKA Open the ORCID record for RYOTARO TANAKA [Opens in a new window]
NAOTO KOMURO
Affiliation:
Department of Mathematics, Hokkaido University of Education, Asahikawa Campus, Asahikawa 070-8621, Japan email [email protected]
KICHI-SUKE SAITO
Affiliation:
Department of Mathematical Sciences, Institute of Science and Technology, Niigata University, Niigata 950-2181, Japan email [email protected]
RYOTARO TANAKA*
Affiliation:
Faculty of Industrial Science and Technology, Tokyo University of Science, Oshamanbe, Hokkaido 049-3514, Japan email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

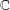In this paper, we give a complete description of left symmetric points for Birkhoff orthogonality in the preduals of von Neumann algebras. As a consequence, except for $\mathbb{C}$, 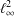$\ell _{\infty }^{2}$ and 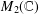$M_{2}(\mathbb{C})$, there are no von Neumann algebras whose preduals have nonzero left symmetric points for Birkhoff orthogonality.

Keywords

von Neumann algebrapredualBirkhoff orthogonalitysymmetric point

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46L99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 3 , December 2018 , pp. 494 - 501
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported in part by Grants-in-Aid for Scientific Research, Grant Numbers 17K05287, 15K04920, Japan Society for the Promotion of Science.

References

Akemann, C. A. and Pedersen, G. K., ‘Facial structure in operator algebra theory’, Proc. Lond. Math. Soc. (3) 64 (1992), 418–448.Google Scholar
Alonso, J., Martini, H. and Wu, S., ‘On Birkhoff orthogonality and isosceles orthogonality in normed linear spaces’, Aequationes Math. 83 (2012), 153–189.Google Scholar
Amir, D., Characterizations of Inner Product Spaces (Birkhäuser Verlag, Basel, 1986).Google Scholar
Arambašić, L. and Rajić, R., ‘On symmetry of the (strong) Birkhoff–James orthogonality in Hilbert C ∗ -modules’, Ann. Funct. Anal. 7 (2016), 17–23.Google Scholar
Edwards, C. M. and Rüttimann, G. T., ‘On the facial structure of the unit balls in a JBW ∗ -triple and its predual’, J. Lond. Math. Soc. (2) 38 (1988), 317–332.Google Scholar
Ghosh, P., Sain, D. and Paul, K., ‘On symmetry of Birkhoff–James orthogonality of linear operators’, Adv. Oper. Theory 2 (2017), 428–434.Google Scholar
James, R. C., ‘Orthogonality and linear functionals in normed linear spaces’, Trans. Amer. Math. Soc. 61 (1947), 265–292.Google Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras. Vol. II, Advanced Theory, Pure and Applied Mathematics, 100 (Academic Press, Orlando, FL, 1986).Google Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras. Vol. IV, Special Topics. Advanced Theory–An Exercise Approach (Birkhäuser, Boston, MA, 1992).Google Scholar
Komuro, N., Saito, K.-S. and Tanaka, R., ‘Symmetric points for (strong) Birkhoff orthogonality in von Neumann algebras with applications to preserver problems’, J. Math. Anal. Appl. 463 (2018), 1109–1131.Google Scholar
Sain, D., ‘Birkhoff–James orthogonality of linear operators on finite dimensional Banach spaces’, J. Math. Anal. Appl. 447 (2017), 860–866.Google Scholar
Sain, D., Ghosh, P. and Paul, K., ‘On symmetry of Birkhoff–James orthogonality of linear operators on finite-dimensional real Banach spaces’, Oper. Matrices 11 (2017), 1087–1095.Google Scholar
Turnšek, A., ‘On operators preserving James’ orthogonality’, Linear Algebra Appl. 407 (2005), 189–195.Google Scholar
Turnšek, A., ‘A remark on orthogonality and symmetry of operators in B(H)’, Linear Algebra Appl. 535 (2017), 141–150.Google Scholar