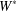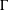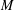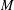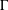3 results
DILATIONS OF INTERACTION GROUPS THAT EXTEND ACTIONS OF ORE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 30 January 2018, pp. 145-161
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
WEAK HAAGERUP PROPERTY OF
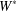 $W^{\ast }$-CROSSED PRODUCTS
$W^{\ast }$-CROSSED PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 31 August 2017, pp. 119-126
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Towards a K-theoretic characterization of graded isomorphisms between Leavitt path algebras
-
- Journal:
- Journal of K-Theory / Volume 14 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 203-245
- Print publication:
- October 2014
-
- Article
- Export citation