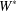Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T06:27:45.346Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAK HAAGERUP PROPERTY OF$W^{\ast }$-CROSSED PRODUCTS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  31 August 2017

QING MENG Open the ORCID record for QING MENG [Opens in a new window]
QING MENG*
Affiliation:
School of Mathematical Sciences, Qufu Normal University, Qufu, Shandong province 273165, China Chern Institute of Mathematics, Nankai University, Tianjin 300071, China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if 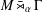$M\,\bar{\rtimes }_{\unicode[STIX]{x1D6FC}}\,\unicode[STIX]{x1D6E4}$ has the weak Haagerup property, then both 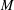$M$ and 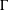$\unicode[STIX]{x1D6E4}$ have the weak Haagerup property, and if 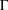$\unicode[STIX]{x1D6E4}$ is an amenable group, then the weak Haagerup property of 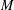$M$ implies that of $M\,\bar{\rtimes }_{\unicode[STIX]{x1D6FC}}\,\unicode[STIX]{x1D6E4}$. We also give a condition under which the weak Haagerup property for 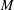$M$ and 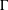$\unicode[STIX]{x1D6E4}$ implies that of 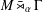$M\,\bar{\rtimes }_{\unicode[STIX]{x1D6FC}}\,\unicode[STIX]{x1D6E4}$.

Keywords

weak Haagerup propertyvon Neumann algebratracial state

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 119 - 126
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Anantharaman, C., ‘Amenable correspondences and approximation properties for von Neumann algebras’, Pacific J. Math. 171 (1995), 309–341.Google Scholar
Brown, N. P. and Ozawa, N., C ∗ -algebras and Finite-Dimensional Approximations, Graduate Studies in Mathematics, 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Dong, Z., ‘Haagerup property for C ∗ -algebras’, J. Math. Anal. Appl. 377 (2011), 631–644.Google Scholar
Haagerup, U. and Kraus, J., ‘Approximation properties for group C*-algebras and group von Neumann algebras’, Trans. Amer. Math. Soc. 344(2) (1994), 667–699.Google Scholar
Jiang, B. J. and Ng, C. K., ‘Property T of reduced C ∗ -crossed products by discrete groups’, Ann. Funct. Anal. 7(3) (2016), 381–385.Google Scholar
Jolissaint, P., ‘Haagerup approximation property for finite von Neumann algebras’, J. Operator Theory 48 (2002), 549–571.Google Scholar
Knudby, S., ‘Semigroups of Herz–Schur multipliers’, J. Funct. Anal. 266(3) (2014), 1565–1610.CrossRefGoogle Scholar
Knudby, S., ‘The weak Haagerup property’, Trans. Amer. Math. Soc. 368 (2014), 3469–3508.CrossRefGoogle Scholar
Leung, C. W. and Ng, C. K., ‘Property (T) and strong property (T) for unital C ∗ -algebras’, J. Funct. Anal. 256 (2009), 3055–3070.CrossRefGoogle Scholar
Mckee, A., Todorov, I. G. and Turowska, L., ‘Herz–Schur multipliers of dynamical systems’, Preprint, 2016, arXiv:1608.01092v1.Google Scholar
Meng, Q., ‘Haagerup property for C ∗ -crossed products’, Bull. Aust. Math. Soc. 95(1) (2017), 144–148.CrossRefGoogle Scholar
Nilsen, M. M. and Smith, R. R., ‘Approximation properties for crossed products by actions and coactions’, Internat. J. Math. 12(5) (2001), 595–608.Google Scholar
Pisier, G., Introduction to Operator Space Theory (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
You, C., ‘Group action preserving the Haagerup property of C ∗ -algebras’, Bull. Aust. Math. Soc. 93 (2016), 295–300.CrossRefGoogle Scholar