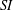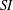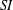We determine sufficient criteria for the prime spectrum of an ambiskew polynomial algebra R over an algebraically closed field 𝕂 to be akin to those of two of the principal examples of such an algebra, namely the universal enveloping algebra U(sl2) (in characteristic 0) and its quantization Uq(sl2) (when q is not a root of unity). More precisely, we determine sufficient criteria for the prime spectrum of R to consist of 0, the ideals (z − λ)R for some central element z of R and all λ ∈ 𝕂, and, for some positive integer d and each positive integer m, d height two prime ideals P for which R/P has Goldie rank m.

The relation between the structure of a ring and the structure of its additive group is studied in the context of some recent results in additive groups of mixed rings. Namely, the notion of the square subgroup of an abelian group, which is a generalization of the concept of nil-group, is considered mainly for mixed non-splitting abelian groups which are the additive groups only of rings whose all subrings are ideals. A non-trivial construction of such a group of finite torsion-free rank no less than two, for which the quotient group modulo the square subgroup is not a nil-group, is given. In particular, a new class of abelian group for which an old problem posed by Stratton and Webb has a negative solution, is indicated. A new, far from obvious, application of rings in which the relation of being an ideal is transitive, is obtained.

This paper presents new results concerning the structure of $\text{SI}$-groups and refines and purifies the results obtained in this field by Shalom Feigelstock [‘Additive groups of rings whose subrings are ideals’, Bull. Aust. Math. Soc.55 (1997), 477–481]. The structure theorem describing torsion-free $\text{SI}$-groups is proved in the associative case. Numerous examples of $\text{SI}$-groups are given. Some inconsistencies in Feigelstock’s article are noted and corrected.

Let $K$ be a field of characteristic zero and $A_{2}:=A_{2}(K)$ the 2$nd$–Weyl algebra over $K$. We establish a close connection between the maximal left ideals of $A_{2}$ and the simple derivations of $K[X_{1},X_{2}]$.

MAIN THEOREM. Let$d = \partial_1 + \beta\partial_2$be a simple derivation of$K[X_1, X_2]$with$\beta\in K[X_1, X_2]$. Then, there exists$\gamma\in K[X_1, X_2]$such that$d + \gamma$generates a maximal left ideal of$A_2$. More precisely, the following is true:

1. $\deg_{X_2} (\beta) \geq 2$ or $\deg_{X_2} (\beta) = 1$ and $\deg_{X_1} (\partial_2(\beta)) \geq 1$;

2. $d + gX_2$generates a maximal left ideal of$A_2$if$g \in K[X_1]\\{0\}$is such that

1. (a) $g \in -(\partial^2_2(\beta)/2)\mathbb{N}$when$\deg_{X_2} (\beta) \geq 2$,

2. (b) $\deg_{X_1} (g) < \deg_{X_1} (\partial_2(\beta))$when$\deg_{X_2} (\beta) = 1$.

As applications, we obtain large families of concrete examples of cyclic maximal left ideals of $A_2$; such examples have been rather scarce so far.