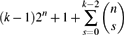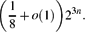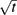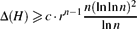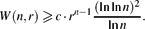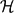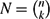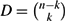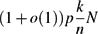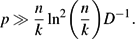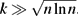10 results
Multicolour Sunflowers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 974-987
-
- Article
- Export citation
On Quantitative Noise Stability and Influences for Discrete and Continuous Models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 23 March 2018, pp. 334-357
-
- Article
- Export citation
Robust Tverberg and Colourful Carathéodory Results via Random Choice
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 19 December 2017, pp. 427-440
-
- Article
- Export citation
Colourings of Uniform Hypergraphs with Large Girth and Applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 245-273
-
- Article
- Export citation
Erdős–Ko–Rado for Random Hypergraphs: Asymptotics and Stability
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 406-422
-
- Article
- Export citation
Existence of Spanning ℱ-Free Subgraphs with Large Minimum Degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 448-467
-
- Article
- Export citation
Secrecy coverage in two dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 1-12
- Print publication:
- March 2016
-
- Article
- Export citation
Minimum Degrees and Codegrees of Ramsey-Minimal 3-Uniform Hypergraphs*†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 850-869
-
- Article
- Export citation
On the Number of Bh-Sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 16 September 2015, pp. 108-129
-
- Article
- Export citation
Semi-Strong Colouring of Intersecting Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 24 October 2013, pp. 1-7
-
- Article
- Export citation