Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T14:05:30.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Erdős–Ko–Rado for Random Hypergraphs: Asymptotics and Stability

Part of: Extremal combinatorics

Published online by Cambridge University Press:  29 March 2017

MARCELO M. GAUY ,
HIÊP HÀN  and
IGOR C. OLIVEIRA
MARCELO M. GAUY
Affiliation:
Institute of Theoretical Computer Science, ETH Zürich, 8092 Zürich, Switzerland
HIÊP HÀN
Affiliation:
Instituto de Matemáticas, Pontificia Universidad Católica de Valparaíso, Blanco Viel 596, Cerro Barón, Valparaíso, Chile
IGOR C. OLIVEIRA
Affiliation:
Faculty of Mathematics and Physics, Charles University in Prague, Sokolovska 83, 186 75 Prague 8, Czech Republic
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the asymptotic version of the Erdős–Ko–Rado theorem for the random k-uniform hypergraph 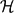$\mathcal{H}$k(n, p). For 2⩽k(n) ⩽ n/2, let 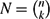$N=\binom{n}k$ and 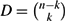$D=\binom{n-k}k$. We show that with probability tending to 1 as n → ∞, the largest intersecting subhypergraph of 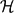$\mathcal{H}$ has size

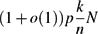$$(1+o(1))p\ffrac kn N$$
for any
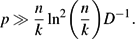$$p\gg \ffrac nk\ln^2\biggl(\ffrac nk\biggr)D^{-1}.$$
 This lower bound on p is asymptotically best possible for k = Θ(n). For this range of k and p, we are able to show stability as well.

A different behaviour occurs when k = o(n). In this case, the lower bound on p is almost optimal. Further, for the small interval D−1 ≪ p ⩽ (n/k)1−ϵD−1, the largest intersecting subhypergraph of 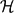$\mathcal{H}$k(n, p) has size Θ(ln(pD)ND−1), provided that 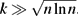$k \gg \sqrt{n \ln n}$.

Together with previous work of Balogh, Bohman and Mubayi, these results settle the asymptotic size of the largest intersecting family in 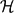$\mathcal{H}$k, for essentially all values of p and k.

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 3 , May 2017 , pp. 406 - 422
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ajtai, M., Komlós, J. and Szemerédi, E. (1980) A note on Ramsey numbers, J. Combin. Theory Ser. A 29 354–360.Google Scholar
[2] Alon, N., Dinur, I., Friedgut, E. and Sudakov, B. (2004) Graph products, Fourier analysis and spectral techniques. Geom. Funct. Anal. 14 913–940.Google Scholar
[3] Balogh, J., Bohman, T. and Mubayi, D. (2009) Erdős–Ko–Rado in random hypergraphs. Combin. Probab. Comput. 18 629–646.CrossRefGoogle Scholar
[4] Balogh, J., Bollobás, B. and Narayanan, B. Transference for the Erdős–Ko–Rado theorem. Forum of Math. Sigma, to appear https://doi.org/10.1017/fms.2015.21.Google Scholar
[5] Balogh, J., Das, S., Delcourt, M., Liu, H. and Sharifzadeh, M. (2015) Intersecting families of discrete structures are typically trivial. J. Combin. Theory Ser. A 132 224–245.Google Scholar
[6] Balogh, J., Morris, R. and Samotij, W. (2015) Independent sets in hypergraphs. J. Amer. Math. Soc. 28 669–709.Google Scholar
[7] Bollobás, B., Narayanan, B. and Raigorodskii, A. On the stability of the Erdős–Ko–Rado theorem. J. Combin. Theory Ser. A, to appear http://dx.doi.org/10.1016/j.jcta.2015.08.002.Google Scholar
[8] Conlon, D. and Gowers, W. Combinatorial theorems in sparse random sets. Submitted DOI 10.4007/annals.2016.184.2.2.Google Scholar
[9] Das, S. and Tran, T. Removal and stability for Erdős–Ko–Rado. SIAM J. Discrete Math., to appear DOI:10.1137/15M105149X.Google Scholar
[10] Devlin, P. and Kahn, J. On stability in the Erdős–Ko–Rado theorem. Submitted DOI:10.1137/15M1012992.Google Scholar
[11] Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. 12 313–320.Google Scholar
[12] Friedgut, E. (2008) On the measure of intersecting families, uniqueness and stability. Combinatorica 28 503–528.Google Scholar
[13] Friedgut, E. and Regev, O. Manuscript.Google Scholar
[14] Hamm, A. and Kahn, J. On Erdős–Ko–Rado for random hypergraphs I. Submitted.Google Scholar
[15] Hamm, A. and Kahn, J. On Erdős–Ko–Rado for random hypergraphs II. Submitted.Google Scholar
[16] Hoffman, A. (1970) On eigenvalues and colorings of graphs. In Graph Theory and its Applications (Proc. Advanced Sem., Math. Research Center, Univ. of Wisconsin), pp. 79–91.Google Scholar
[17] Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley-Interscience.Google Scholar
[18] Kleitman, D. and Winston, K. (1982) On the number of graphs without 4-cycles. Discrete Math. 41 167–172.Google Scholar
[19] Kohayakawa, Y., Kreuter, B. and Steger, A. (1998) An extremal problem for random graphs and the number of graphs with large even-girth. Combinatorica 18 101–120.Google Scholar
[20] Kohayakawa, Y., Lee, S. J., Rödl, V. and Samotij, W. (2015) The number of Sidon sets and the maximum size of Sidon sets contained in a sparse random set of integers. Random Struct. Alg. 46 1–25.Google Scholar
[21] Lovász, L. (1979) On the Shannon capacity of a graph. IEEE Trans. Inform. Theory 25 1–7.Google Scholar
[22] Samotij, W. (2014) Stability results for random discrete structures. Random Struct. Alg. 44 269–289.Google Scholar
[23] Saxton, D. and Thomason, A. (2015) Hypergraph containers. Invent. Math. 201 925–992.Google Scholar
[24] Schacht, M. Extremal results for random discrete structures. Submitted DOI 10.4007/annals.2016.184.2.1.Google Scholar
[25] Shearer, J. (1983) A note on the independence number of triangle-free graphs. Discrete Math. 46 83–87.Google Scholar