4 results
Stochastic Comparisons of Residual Lifetimes and Inactivity Times of Coherent Systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 848-860
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Conditional Ordering of k-out-of-n Systems with Independent But Nonidentical Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1113-1125
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On the behaviour of some new ageing properties based upon the residual life of k-out-of-n systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-433
- Print publication:
- June 2002
-
- Article
- Export citation
Convexity of a set of stochastically ordered random variables
-
- Journal:
- Advances in Applied Probability / Volume 22 / Issue 1 / March 1990
- Published online by Cambridge University Press:
- 01 July 2016, pp. 160-177
- Print publication:
- March 1990
-
- Article
- Export citation

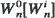 be the waiting time of the
be the waiting time of the 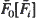 and service time survival function
and service time survival function 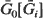 . Using the above convexity result it is shown that if
. Using the above convexity result it is shown that if 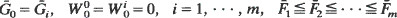 and for some
and for some 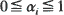 such that
such that 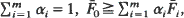 then
then 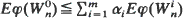 for all increasing convex functions
for all increasing convex functions 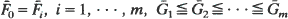 and
and 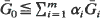 is also obtained. Other examples are also included.
is also obtained. Other examples are also included.