Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T17:01:52.692Z Has data issue: false hasContentIssue false
  • English
  • Français

Convexity of a set of stochastically ordered random variables

Published online by Cambridge University Press:  01 July 2016

Moshe Shaked  and
J. George Shanthikumar
Moshe Shaked*
Affiliation:
University of Arizona
J. George Shanthikumar*
Affiliation:
University of California, Berkeley
*
∗Postal address: Department of Mathematics Building # 89, The University of Arizona, Tucson, AZ 85721, USA.
∗∗Postal address: School of Business Administration, 350 Barrows Hall, University of California, Berkeley, CA94720, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that a set of random variables with increasing and convex (concave) survival functions are stochastically increasing and convex (concave) in the sample path sense. This stochastic convexity (concavity) result is then used to establish convexity (concavity) results for (i) a single-server queueing system with a time-out control policy, (ii) residual life, (iii) stationary renewal excess life and (iv) M/G/1 queues. These results are new and could not be derived without the direct or indirect aid of the above stochastic convexity (concavity) result. Furthermore, we illustrate that the above stochastic convexity (concavity) result can be applied to obtain new bounds for queueing systems. Specifically, let 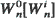be the waiting time of the nth customer in a GI/G/1 queue with inter-arrival time survival function 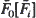and service time survival function 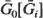. Using the above convexity result it is shown that if 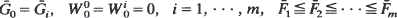and for some 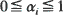such that 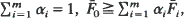then 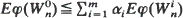for all increasing convex functions φ, whenever the expectations exist. A similar result for 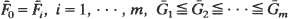and is also obtained. Other examples are also included.

Keywords

STOCHASTIC CONVEXITYSTOCHASTIC ORDERINGGI/G/1 QUEUECONTROLLED ARRIVAL QUEUERESIDUAL LIFESTATIONARY RENEWAL EXCESS LIFE
Type
Research Article
Information
Advances in Applied Probability , Volume 22 , Issue 1 , March 1990 , pp. 160 - 177
Copyright
Copyright © Applied Probability Trust 1990 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by the Air Force Office of Scientific Research, USAF under Grant AFOSR-84–0205. Reproduction in whole or in part is permitted for any purpose by the United States Government.

References

[1] Berg, M. and Cleroux, R. (1982) A marginal cost analysis for an age replacement policy with minimal repair. INFOR 20, 258–263.Google Scholar
[2] Brown, M. and Proschan, F. (1983) Imperfect repair. J. Appl. Prob. 20, 851–859.CrossRefGoogle Scholar
[3] Cambanis, S. and Simons, G. (1982) Probability and expectation inequalities Z. Wahrscheinlichkeitsth. 59, 1–25.CrossRefGoogle Scholar
[4] Cleroux, R., Duboc, S. and Tilquin, C. (1979) The age replacement problem with minimal repair and random repair costs. Operat. Res. 27, 1158–1167.CrossRefGoogle Scholar
[5] Daley, D. J. and Rolski, T. (1984) Some comparability results for waiting times in single- and many-server queues. J. Appl. Prob. 21, 887–900.CrossRefGoogle Scholar
[6] Grassmann, W. (1983) The convexity of the mean queue size of the M/M/c queue with respect to the traffic intensity. J. Appl. Prob. 20, 916–919.CrossRefGoogle Scholar
[7] Harel, A. and Zipkin, P. (1984) Strong convexity results for queueing systems with applications in production and telecommunications. Technical Report, Graduate School of Business, Columbia University.Google Scholar
[8] Kamae, T., Krengel, U. and O'Brien, G. (1977) Stochastic inequalities on partially ordered spaces. Ann. Prob. 5, 899–912.CrossRefGoogle Scholar
[9] Lee, H. L. and Cohen, M. A. (1983) A note on the convexity of performance measures of M/M/c queueing systems. J. Appl. Prob. 20, 920–923.CrossRefGoogle Scholar
[10] Rolski, T. (1986) Upper bounds for single server queues with doubly stochastic Poisson arrivals. Math. Operat. Res. 11, 442–450.CrossRefGoogle Scholar
[11] Samaratunga, C. (1986) Open-loop routing policies for queueing systems. Summer paper, School of Business Administration, University of California, Berkeley.Google Scholar
[12] Shaked, M. and Shanthikumar, J. G. (1988a) Stochastic convexity and its applications. Adv. Appl. Prob. 20, 427–446.CrossRefGoogle Scholar
[13] Shaked, M. and Shanthikumar, J. G. (1988b) Temporal stochastic convexity and concavity. Stoch. Proc. Appl. 27, 1–20.CrossRefGoogle Scholar
[14] Shanthikumar, J. G. and Yao, D. D. (1987) Optimal server allocation in a system of multi-server stations. Management Sci. 33, 1173–1180.CrossRefGoogle Scholar
[15] Stoyan, D. (1983) Comparison Methods for Queues and other Stochastic Models. Wiley, New York.Google Scholar
[16] Whitt, W. (1981) Comparing counting processes and queues. Adv. Appl. Prob. 13, 207–220.CrossRefGoogle Scholar
[17] Yao, D. D. and Shanthikumar, J. G. (1989) Allocating a joint setup in a multi-cell system. Ann. Operat. Res. CrossRefGoogle Scholar
[18] Yao, D. D. and Shanthikumar, J. G. (1987) The optimal input rates to a system of manufacturing cells. INFOR 25, 57–75.Google Scholar