19 results
9 - The Bitter End
-
- Book:
- A ‘Constitution for the Oceans'
- Published online:
- 06 February 2025
- Print publication:
- 13 February 2025, pp 293-322
-
- Chapter
- Export citation
8 - System Reliability
-
- Book:
- Structural and System Reliability
- Published online:
- 13 January 2022
- Print publication:
- 13 January 2022, pp 200-261
-
- Chapter
- Export citation
Stochastic comparison of parallel systems with Pareto components
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 20 May 2021, pp. 950-962
-
- Article
- Export citation
STOCHASTIC ORDERING OF LIFETIMES OF PARALLEL AND SERIES SYSTEMS COMPRISING HETEROGENEOUS DEPENDENT COMPONENTS WITH GENERALIZED BIRNBAUM-SAUNDERS DISTRIBUTIONS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 25 August 2020, pp. 49-65
-
- Article
- Export citation
ON VARIABILITY OF SERIES AND PARALLEL SYSTEMS WITH HETEROGENEOUS COMPONENTS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. 626-645
-
- Article
- Export citation
Hazard rate ordering of the largest order statistics from geometric random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 652-658
- Print publication:
- June 2018
-
- Article
- Export citation
Stochastic comparison of parallel systems with heterogeneous exponential components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 970-976
- Print publication:
- September 2017
-
- Article
- Export citation
LIKELIHOOD RATIO ORDERING OF PARALLEL SYSTEMS WITH HETEROGENEOUS SCALED COMPONENTS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 32 / Issue 3 / July 2018
- Published online by Cambridge University Press:
- 05 June 2017, pp. 460-468
-
- Article
- Export citation
Reducing Response Time in Fork-Join Systems under Heavy Traffic Via Imbalance Control
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1137-1156
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Signatures of Coherent Systems Built with Separate Modules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 843-855
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
On the behaviour of some new ageing properties based upon the residual life of k-out-of-n systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-433
- Print publication:
- June 2002
-
- Article
- Export citation
A general shock model for a reliability system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 925-935
- Print publication:
- December 2000
-
- Article
- Export citation
A general formula for the downtime distribution of a parallel system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 772-785
- Print publication:
- September 1996
-
- Article
- Export citation
Max-infinite divisibility and multivariate total positivity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 721-730
- Print publication:
- September 1994
-
- Article
- Export citation
Laplace ordering and its applications
-
- Journal:
- Journal of Applied Probability / Volume 28 / Issue 1 / March 1991
- Published online by Cambridge University Press:
- 14 July 2016, pp. 116-130
- Print publication:
- March 1991
-
- Article
- Export citation
Optimal number of units for a parallel system
-
- Journal:
- Journal of Applied Probability / Volume 21 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 14 July 2016, pp. 431-436
- Print publication:
- June 1984
-
- Article
- Export citation
Further results of replacement problem of a parallel system in random environment
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 923-926
- Print publication:
- December 1979
-
- Article
- Export citation
Replacement problem of a parallel system in random environment
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 1 / March 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 203-205
- Print publication:
- March 1979
-
- Article
- Export citation
Reliability systems in random environment
-
- Journal:
- Journal of Applied Probability / Volume 13 / Issue 2 / June 1976
- Published online by Cambridge University Press:
- 14 July 2016, pp. 407-410
- Print publication:
- June 1976
-
- Article
- Export citation

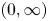
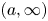
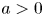
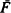 is Laplace-smaller than
is Laplace-smaller than 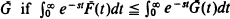 for all
for all 