4 results
2 - Martingales
- from Part I - Tools and Theory
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 50-74
-
- Chapter
- Export citation
3 - Martingales and Potentials
-
- Book:
- Modern Discrete Probability
- Published online:
- 14 December 2023
- Print publication:
- 18 January 2024, pp 95-181
-
- Chapter
- Export citation
The maximum in critical Galton–Watson and birth and death processes
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue 3 / September 1986
- Published online by Cambridge University Press:
- 14 July 2016, pp. 601-613
- Print publication:
- September 1986
-
- Article
- Export citation
The fair charge on a car ferry
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 3 / September 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 654-661
- Print publication:
- September 1980
-
- Article
- Export citation


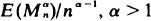 with
with 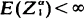 . If (
. If (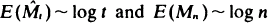 thereof.
thereof.