Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pakes, Anthony G.
1987.
Remarks on the maxima of a martingale sequence with application to the simple critical branching process.
Journal of Applied Probability,
Vol. 24,
Issue. 03,
p.
768.
Pakes, Anthony G.
1987.
Remarks on the maxima of a martingale sequence with application to the simple critical branching process.
Journal of Applied Probability,
Vol. 24,
Issue. 3,
p.
768.
Weiner, Howard J.
1988.
Joint Moments of the Maximum in a Critical Branching Process.
Journal of Information and Optimization Sciences,
Vol. 9,
Issue. 1,
p.
141.
Troutman, B. M.
and
Karlinger, M. R.
1989.
Predictors of the peak width for networks with exponential links.
Stochastic Hydrology and Hydraulics,
Vol. 3,
Issue. 1,
p.
1.
Spåtaru, Aurel
1991.
A maximum sequence in a critical multitype branching process.
Journal of Applied Probability,
Vol. 28,
Issue. 4,
p.
893.
Spåtaru, Aurel
1991.
A maximum sequence in a critical multitype branching process.
Journal of Applied Probability,
Vol. 28,
Issue. 04,
p.
893.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Borovkov, K. A.
and
Vatutin, V A.
1996.
On distribution tails and expectations of maxima in critical branching processes.
Journal of Applied Probability,
Vol. 33,
Issue. 3,
p.
614.
Borovkov, K. A.
and
Vatutin, V A.
1996.
On distribution tails and expectations of maxima in critical branching processes.
Journal of Applied Probability,
Vol. 33,
Issue. 03,
p.
614.
Pakes, Anthony G.
1998.
A limit theorem for the maxima of the para-critical simple branching process.
Advances in Applied Probability,
Vol. 30,
Issue. 3,
p.
740.
Pakes, Anthony G.
1998.
A limit theorem for the maxima of the para-critical simple branching process.
Advances in Applied Probability,
Vol. 30,
Issue. 3,
p.
740.
Topchii, V. A.
and
Vatutin, V. A.
1998.
Maximum of the Critical Galton--Watson Processes and Left-Continuous Random Walks.
Theory of Probability & Its Applications,
Vol. 42,
Issue. 1,
p.
17.
Ватутин, Владимир Алексеевич
Vatutin, Vladimir Alekseevich
Вахтель, Виталий Иванович
Vakhtel', Vitalii Ivanovich
Фляйшманн, К
and
Fleischmann, Klaus
2007.
Критические процессы Гальтона - Ватсона: Максимум общего числа частиц внутри большого окна.
Теория вероятностей и ее применения,
Vol. 52,
Issue. 3,
p.
419.
Vatutin, V. A.
Wachtel, V.
and
Fleischmann, K.
2008.
Critical Galton–Watson Processes: The Maximum of Total Progenies within a Large Window.
Theory of Probability & Its Applications,
Vol. 52,
Issue. 3,
p.
470.
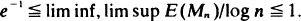 Explicit asymptotic bounds are given for
Explicit asymptotic bounds are given for 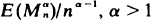 with
with 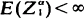 . If (Zn)n has a linear fractional offspring distribution, it can be embedded in a critical birth and death process (Ẑ t)t. Using martingale methods one obtains
. If (Zn)n has a linear fractional offspring distribution, it can be embedded in a critical birth and death process (Ẑ t)t. Using martingale methods one obtains  thereof.
thereof.