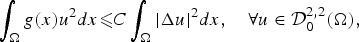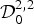Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • Muckenhoupt Class Weight Decomposition and BMO Distance to Bounded Functions

  • Part of
  • Morten Nielsen, Hrvoje Šikić
  • Journal:
    Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
    Published online by Cambridge University Press:
    25 March 2019, pp. 1017-1031

  • We study the connection between the Muckenhoupt Ap weights and bounded mean oscillation (BMO) for general bases for ℝd. New classes of bases are introduced that allow for several deep results on the Muckenhoupt weights–BMO connection to hold in a very general form. The John–Nirenberg type inequality and its consequences are valid for the new class of Calderón–Zygmund bases which includes cubes in ℝd, but also the basis of rectangles in ℝd. Of particular interest to us is the Garnett–Jones theorem on the BMO distance, which is valid for cubes. We prove that the theorem is equivalent to the newly introduced A2-decomposition property of bases. Several sufficient conditions for the theorem to hold are analysed as well. However, the question whether the theorem fully holds for rectangles remains open.

  • On the generalized Hardy-Rellich inequalities

  • Part of
  • T.V. Anoop, Ujjal Das, Abhishek Sarkar
  • Journal:
    Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
    Published online by Cambridge University Press:
    26 January 2019, pp. 897-919
    Print publication:
    April 2020

  • In this paper, we look for the weight functions (say g) that admit the following generalized Hardy-Rellich type inequality:

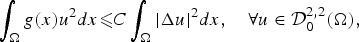    $$\int_\Omega g (x)u^2 dx \les C\int_\Omega \vert \Delta u \vert ^2 dx,\quad \forall u\in {\rm {\cal D}}_0^{2,2} (\Omega ),$$
    for some constant C > 0, where Ω is an open set in ℝN with N ⩾ 1. We find various classes of such weight functions, depending on the dimension N and the geometry of Ω. Firstly, we use the Muckenhoupt condition for the one-dimensional weighted Hardy inequalities and a symmetrization inequality to obtain admissible weights in certain Lorentz-Zygmund spaces. Secondly, using the fundamental theorem of integration we obtain the weight functions in certain weighted Lebesgue spaces. As a consequence of our results, we obtain simple proofs for the embeddings of 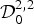${\cal D}_0^{2,2} $ into certain Lorentz-Zygmund spaces proved by Hansson and later by Brezis and Wainger.