We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that under mild conditions, the connected sum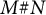 
$M\# N$ of simply connected, closed, orientable n-dimensional Poincaré Duality complexes M and N is hyperbolic and has no homotopy exponent at all but finitely many primes, verifying a weak version of Moore’s conjecture. This is derived from an elementary framework involving 
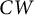$CW$-complexes satisfying certain conditions.
