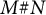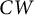1 Introduction
Let X be a pointed, simply connected finite
![]() $CW$
-complex. It is said to be elliptic if the rank of
$CW$
-complex. It is said to be elliptic if the rank of
![]() $\pi _{\ast }(X)\otimes \mathbb {Q}$
is finite and is otherwise hyperbolic. The rational dichotomy of Félix, Halperin, and Thomas [Reference Félix, Halperin and ThomasFHT, Chapter 33] says that, remarkably, if X is hyperbolic, then the rank of
$\pi _{\ast }(X)\otimes \mathbb {Q}$
is finite and is otherwise hyperbolic. The rational dichotomy of Félix, Halperin, and Thomas [Reference Félix, Halperin and ThomasFHT, Chapter 33] says that, remarkably, if X is hyperbolic, then the rank of
![]() $\oplus _{k=2}^{m}(\pi _{k}(X)\otimes \mathbb {Q})$
grows exponentially with m. In particular, there is no hyperbolic space whose rational homotopy groups have polynomial growth. Classifying those spaces that are elliptic or hyperbolic is a major problem in rational homotopy theory.
$\oplus _{k=2}^{m}(\pi _{k}(X)\otimes \mathbb {Q})$
grows exponentially with m. In particular, there is no hyperbolic space whose rational homotopy groups have polynomial growth. Classifying those spaces that are elliptic or hyperbolic is a major problem in rational homotopy theory.
Turning to torsion homotopy groups, for a fixed prime p, the homotopy exponent of X is the least power of p that annihilates the p-torsion in
![]() $\pi _{\ast }(X)$
. If this least power is
$\pi _{\ast }(X)$
. If this least power is
![]() $p^{r}$
, write
$p^{r}$
, write
![]() $\exp _{p}(X)=p^{r}$
. If no such power exists, that is, if
$\exp _{p}(X)=p^{r}$
. If no such power exists, that is, if
![]() $\pi _{\ast }(X)$
has p-torsion of arbitrarily high order, then write
$\pi _{\ast }(X)$
has p-torsion of arbitrarily high order, then write
![]() $\exp _{p}(X)=\infty $
. Determining precise exponents, or at least good exponent bounds, is a major problem in unstable homotopy theory.
$\exp _{p}(X)=\infty $
. Determining precise exponents, or at least good exponent bounds, is a major problem in unstable homotopy theory.
Moore’s conjecture posits a deep relationship between the rational and torsion homotopy groups.
Conjecture 1.1 (Moore)
Let X be a simply connected finite dimensional
![]() $CW$
-complex. Then the following are equivalent:
$CW$
-complex. Then the following are equivalent:
-
(a) X is elliptic.
-
(b)
 $\exp _{p}(X)<\infty $
for some prime p.
$\exp _{p}(X)<\infty $
for some prime p. -
(c)
 $\exp _{p}(X)<\infty $
for all primes p.
$\exp _{p}(X)<\infty $
for all primes p.
As prototypes, a sphere is rationally elliptic and has finite exponent at
![]() $2$
by James [Reference JamesJ2] and at odd primes by Toda [Reference TodaTo]. A wedge of two or more spheres is hyperbolic by the Hilton–Milnor theorem and has no exponent at any prime p by [Reference NeisendorferNS]. Moore’s conjecture is known to hold for several families of spaces, including torsion-free suspensions [Reference SelickSe2], odd primary Moore spaces [Reference Neisendorfer and SelickN], finite H-spaces [Reference LongL], H-spaces with finitely generated homology [Reference Chachólski, Pitsch, Scherer and StanleyCPSS], most spaces with two or three cells [Reference NeisendorferNS], moment-angle complexes and generalized moment-angle complexes [Reference Hao, Sun and TheriaultHST], real moment-angle complexes [Reference KimK], and certain families of Poincaré Duality complexes [Reference Basu and BasuBB, Reference Beben and TheriaultBT, Reference TheriaultTh] such as those that are
$2$
by James [Reference JamesJ2] and at odd primes by Toda [Reference TodaTo]. A wedge of two or more spheres is hyperbolic by the Hilton–Milnor theorem and has no exponent at any prime p by [Reference NeisendorferNS]. Moore’s conjecture is known to hold for several families of spaces, including torsion-free suspensions [Reference SelickSe2], odd primary Moore spaces [Reference Neisendorfer and SelickN], finite H-spaces [Reference LongL], H-spaces with finitely generated homology [Reference Chachólski, Pitsch, Scherer and StanleyCPSS], most spaces with two or three cells [Reference NeisendorferNS], moment-angle complexes and generalized moment-angle complexes [Reference Hao, Sun and TheriaultHST], real moment-angle complexes [Reference KimK], and certain families of Poincaré Duality complexes [Reference Basu and BasuBB, Reference Beben and TheriaultBT, Reference TheriaultTh] such as those that are
![]() $(n-1)$
-connected and
$(n-1)$
-connected and
![]() $2n$
-dimensional. There are also some partial results: a hyperbolic loop space with p-torsion-free homology has no exponent at p [Reference StelzerSt], an elliptic space has a finite exponent at all but finitely many primes [Reference McGibbon and WilkersonMW], and a
$2n$
-dimensional. There are also some partial results: a hyperbolic loop space with p-torsion-free homology has no exponent at p [Reference StelzerSt], an elliptic space has a finite exponent at all but finitely many primes [Reference McGibbon and WilkersonMW], and a
![]() $2$
-cone satisfies Moore’s conjecture at all but finitely many primes [Reference AnickA].
$2$
-cone satisfies Moore’s conjecture at all but finitely many primes [Reference AnickA].
In this paper, we consider Moore’s conjecture in the context of connected sums of Poincaré Duality complexes. Our main result is of the “all but finitely many primes” form, although there is an integral result in a special case. The statement of the result depends on Hurewicz images and localization. Let
![]() $h_{\ast }(X;\mathbb {Q})$
be the submodule of
$h_{\ast }(X;\mathbb {Q})$
be the submodule of
![]() $H_{\ast }(X;\mathbb {Q})$
that consists of Hurewicz images.
$H_{\ast }(X;\mathbb {Q})$
that consists of Hurewicz images.
Theorem 1.2 Let M and N be simply connected, closed, orientable n-dimensional Poincaré Duality complexes. Suppose that M and N are not rationally homotopy equivalent to
![]() $S^{n}$
and one of
$S^{n}$
and one of
![]() $h_{\ast }(M;\mathbb {Q})$
or
$h_{\ast }(M;\mathbb {Q})$
or
![]() $h_{\ast }(N;\mathbb {Q})$
has either a generator in odd degree or rank
$h_{\ast }(N;\mathbb {Q})$
has either a generator in odd degree or rank
![]() $\geq 2$
. Then
$\geq 2$
. Then
![]() $M\# N$
is hyperbolic and has no exponent at all but finitely many primes.
$M\# N$
is hyperbolic and has no exponent at all but finitely many primes.
The hypotheses on M and N are rational. To tease out what they are saying, observe that the condition that M and N are not rationally homotopy equivalent to
![]() $S^{n}$
implies that the
$S^{n}$
implies that the
![]() $(n-1)$
-skeletons of M and N are not rationally contractible. Rationally, there is a Hurewicz image in the
$(n-1)$
-skeletons of M and N are not rationally contractible. Rationally, there is a Hurewicz image in the
![]() $(n-1)$
-skeleton in each case coming from the inclusion of the bottom cell. So the ranks of
$(n-1)$
-skeleton in each case coming from the inclusion of the bottom cell. So the ranks of
![]() $h_{\ast }(M;\mathbb {Q})$
and
$h_{\ast }(M;\mathbb {Q})$
and
![]() $h_{\ast }(N;\mathbb {Q})$
are both
$h_{\ast }(N;\mathbb {Q})$
are both
![]() $\geq 1$
. If one of these Hurewicz images is in odd degree, then the hypotheses of Theorem 1.2 are fulfilled. Otherwise, all Hurewicz images are concentrated in even degrees and the additional hypothesis that the rank one of
$\geq 1$
. If one of these Hurewicz images is in odd degree, then the hypotheses of Theorem 1.2 are fulfilled. Otherwise, all Hurewicz images are concentrated in even degrees and the additional hypothesis that the rank one of
![]() $h_{\ast }(M;\mathbb {Q})$
or
$h_{\ast }(M;\mathbb {Q})$
or
![]() $h_{\ast }(N;\mathbb {Q})$
is
$h_{\ast }(N;\mathbb {Q})$
is
![]() $\geq 2$
is invoked. In general, this additional hypothesis is needed: an example follows the statement of Theorem 1.3.
$\geq 2$
is invoked. In general, this additional hypothesis is needed: an example follows the statement of Theorem 1.3.
The exact set of primes that are inverted is identified in the proof. There are two types. First, a rational Hurewicz image corresponds to a map whose integral Hurewicz image may be divisible by a finite number. We localize away from the primes dividing that number, and do so for the two or three Hurewicz images needed depending on the rank conditions on
![]() $h_{\ast }(M;\mathbb {Q})$
and
$h_{\ast }(M;\mathbb {Q})$
and
![]() $h_{\ast }(N;\mathbb {Q})$
. Second, these Hurewicz images have cohomological duals that correspond to maps to Eilenberg–MacLane spaces. We invert sufficient primes to approximate these Eilenberg–MacLane spaces through dimension n by spaces Y with the property that
$h_{\ast }(N;\mathbb {Q})$
. Second, these Hurewicz images have cohomological duals that correspond to maps to Eilenberg–MacLane spaces. We invert sufficient primes to approximate these Eilenberg–MacLane spaces through dimension n by spaces Y with the property that
![]() $\Sigma \Omega Y$
is homotopy equivalent to a wedge of spheres.
$\Sigma \Omega Y$
is homotopy equivalent to a wedge of spheres.
The strategy of proof is to show that after localizing at a prime p not in the finite set of excluded primes, there is a wedge W of at least two simply connected spheres with the property that
![]() $\Omega W$
retracts off
$\Omega W$
retracts off
![]() $\Omega (M\# N)$
. Then, as W is hyperbolic and has no exponent at p, it follows that
$\Omega (M\# N)$
. Then, as W is hyperbolic and has no exponent at p, it follows that
![]() $M\# N$
is hyperbolic and has no exponent at p. In fact, the proof works in the more general context of a certain family of
$M\# N$
is hyperbolic and has no exponent at p. In fact, the proof works in the more general context of a certain family of
![]() $CW$
-complexes, as described in Section 3.
$CW$
-complexes, as described in Section 3.
There is a special case for which no localization is necessary. If M and N are simply connected and both
![]() $H_{2}(M;\mathbb {Z})$
and
$H_{2}(M;\mathbb {Z})$
and
![]() $H_{2}(N;\mathbb {Z})$
have integral summands, these are Hurewicz images, so we may dispense with the first type of prime to invert. We may dispense with the second type of prime as, in this case,
$H_{2}(N;\mathbb {Z})$
have integral summands, these are Hurewicz images, so we may dispense with the first type of prime to invert. We may dispense with the second type of prime as, in this case,
![]() $\Omega K(\mathbb {Z},2)\simeq S^{1}$
is already a sphere.
$\Omega K(\mathbb {Z},2)\simeq S^{1}$
is already a sphere.
Theorem 1.3 Let M and N be simply connected, closed, orientable n-dimensional Poincaré Duality complexes where
![]() $n\geq 3$
. Suppose that
$n\geq 3$
. Suppose that
![]() $H_{2}(M;\mathbb {Z})$
has a
$H_{2}(M;\mathbb {Z})$
has a
![]() $\mathbb {Z}$
-module summand and
$\mathbb {Z}$
-module summand and
![]() $H_{2}(N;\mathbb {Z})$
has a
$H_{2}(N;\mathbb {Z})$
has a
![]() $\mathbb {Z}\oplus \mathbb {Z}$
-module summand. Then
$\mathbb {Z}\oplus \mathbb {Z}$
-module summand. Then
![]() $M\# N$
is hyperbolic and has no exponent at any prime p.
$M\# N$
is hyperbolic and has no exponent at any prime p.
For example, let N be a Poincaré Duality complex of dimension
![]() $2n$
with
$2n$
with
![]() $\mbox {rank}\ H_{2}(N;\mathbb {Z})\geq 2$
. Then
$\mbox {rank}\ H_{2}(N;\mathbb {Z})\geq 2$
. Then
![]() $\mathbb {C}P^{n}\# N$
is hyperbolic and has no exponent at any prime p.
$\mathbb {C}P^{n}\# N$
is hyperbolic and has no exponent at any prime p.
The condition on the rank of
![]() $H_{2}(N;\mathbb {Z})$
is best possible in the sense that
$H_{2}(N;\mathbb {Z})$
is best possible in the sense that
![]() $\mathbb {C}P^{n}\#\mathbb {C}P^{n}$
is known to be elliptic. Further, by [Reference Huang and TheriaultHT], if
$\mathbb {C}P^{n}\#\mathbb {C}P^{n}$
is known to be elliptic. Further, by [Reference Huang and TheriaultHT], if
![]() $n=2m$
, then there is a homotopy equivalence
$n=2m$
, then there is a homotopy equivalence
![]() $\Omega (\mathbb {C}P^{2m}\#\mathbb {C}P^{2m})\simeq S^{1}\times S^{1}\times \Omega S^{3}\times \Omega S^{4m-1}$
and if
$\Omega (\mathbb {C}P^{2m}\#\mathbb {C}P^{2m})\simeq S^{1}\times S^{1}\times \Omega S^{3}\times \Omega S^{4m-1}$
and if
![]() $n=2m+1$
, then, after localizing away from
$n=2m+1$
, then, after localizing away from
![]() $2$
, there is a homotopy equivalence
$2$
, there is a homotopy equivalence
![]() $\Omega (\mathbb {C}P^{2m+1}\#\mathbb {C}P^{2m+1})\simeq S^{1}\times S^{1}\times \Omega S^{3}\times \Omega S^{4m+1}$
. Thus, if n is even, then
$\Omega (\mathbb {C}P^{2m+1}\#\mathbb {C}P^{2m+1})\simeq S^{1}\times S^{1}\times \Omega S^{3}\times \Omega S^{4m+1}$
. Thus, if n is even, then
![]() $\mathbb {C}P^{n}\#\mathbb {C}P^{n}$
has a finite homotopy exponent at every prime p, and if n is odd, then
$\mathbb {C}P^{n}\#\mathbb {C}P^{n}$
has a finite homotopy exponent at every prime p, and if n is odd, then
![]() $\mathbb {C}P^{n}\#\mathbb {C}P^{n}$
has a finite homotopy exponent at every odd prime.
$\mathbb {C}P^{n}\#\mathbb {C}P^{n}$
has a finite homotopy exponent at every odd prime.
In the last section of the paper, a generalization is made to bundles over connected sums.
2 Some properties of the James construction
Let X be a pointed, path-connected space. For
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $X^{\times n}$
and
$X^{\times n}$
and
![]() $X^{\wedge n}$
, respectively, be the n-fold product and smash product of X with itself. Define
$X^{\wedge n}$
, respectively, be the n-fold product and smash product of X with itself. Define
![]() $J_{n}(X)$
as the quotient space
$J_{n}(X)$
as the quotient space
where
![]() $(x_{1},\ldots ,x_{i-1},\ast ,x_{i+1},x_{i+2},\ldots ,x_{n})\sim (x_{1},\ldots ,x_{i-1},x_{i+1},\ast ,x_{i+2},\ldots ,x_{n})$
. Observe that there is an inclusion
$(x_{1},\ldots ,x_{i-1},\ast ,x_{i+1},x_{i+2},\ldots ,x_{n})\sim (x_{1},\ldots ,x_{i-1},x_{i+1},\ast ,x_{i+2},\ldots ,x_{n})$
. Observe that there is an inclusion
given by sending
![]() $(x_{1},\ldots ,x_{n})$
to
$(x_{1},\ldots ,x_{n})$
to
![]() $(x_{1},\ldots ,x_{n},\ast )$
. Let
$(x_{1},\ldots ,x_{n},\ast )$
. Let
The space
![]() $J(X)$
is called the James construction on X.
$J(X)$
is called the James construction on X.
Concatenation of sequences gives
![]() $J(X)$
the structure of an associative monoid. James [Reference JamesJ] showed that there is a homotopy equivalence of H-spaces
$J(X)$
the structure of an associative monoid. James [Reference JamesJ] showed that there is a homotopy equivalence of H-spaces
He used this to give a homotopy decomposition of
![]() $\Sigma \Omega \Sigma X$
.
$\Sigma \Omega \Sigma X$
.
Lemma 2.1 Let X be a pointed, path-connected space. Then there is a homotopy equivalence
Now, specialize to the case where
![]() $X=S^{2m}$
and localize at a prime p. There is a homotopy fibration (the
$X=S^{2m}$
and localize at a prime p. There is a homotopy fibration (the
![]() $EHP$
fibration)
$EHP$
fibration)
where E is the inclusion of
![]() $J_{p-1}(S^{2m})$
into
$J_{p-1}(S^{2m})$
into
![]() $J(S^{2m})\simeq \Omega S^{2m+1}$
and H is the
$J(S^{2m})\simeq \Omega S^{2m+1}$
and H is the
![]() $p^{th}$
-James-Hopf invariant. The space
$p^{th}$
-James-Hopf invariant. The space
![]() $J_{p-1}(S^{2m})$
will play an important role in what follows. Three properties are needed.
$J_{p-1}(S^{2m})$
will play an important role in what follows. Three properties are needed.
First, if
![]() $p=2$
, then
$p=2$
, then
![]() $J_{p-1}(S^{2m})=S^{2m}$
and
$J_{p-1}(S^{2m})=S^{2m}$
and
![]() $\Sigma \Omega S^{2m}$
decomposes as a wedge of spheres by Lemma 2.1. Moore (a proof appears in [Reference SelickSe1]) proved an analogous result for odd primes. Let
$\Sigma \Omega S^{2m}$
decomposes as a wedge of spheres by Lemma 2.1. Moore (a proof appears in [Reference SelickSe1]) proved an analogous result for odd primes. Let
be the inclusion of the bottom cell.
Lemma 2.2 If p is odd and
![]() $m\geq 1$
, the space
$m\geq 1$
, the space
![]() $\Sigma \Omega J_{p-1}(S^{2m})$
is homotopy equivalent to a wedge of spheres. In particular,
$\Sigma \Omega J_{p-1}(S^{2m})$
is homotopy equivalent to a wedge of spheres. In particular,
![]() $\Sigma \varepsilon _{2m}$
has a left homotopy inverse.
$\Sigma \varepsilon _{2m}$
has a left homotopy inverse.
Corollary 2.3 If p is odd and
![]() $m,n\geq 1$
, then the map
$m,n\geq 1$
, then the map
has a left homotopy inverse.
Proof By Lemma 2.2,
![]() $\Sigma \varepsilon _{2m}$
has a right homotopy inverse
$\Sigma \varepsilon _{2m}$
has a right homotopy inverse
![]() $\delta _{2m}\colon {\Sigma \Omega J_{p-1}(S^{2m})}\stackrel {{}}{\longrightarrow } {\Sigma S^{2m-1}} $
. The composite
$\delta _{2m}\colon {\Sigma \Omega J_{p-1}(S^{2m})}\stackrel {{}}{\longrightarrow } {\Sigma S^{2m-1}} $
. The composite

is therefore a left homotopy inverse for
![]() $\Sigma \varepsilon _{2m}\wedge \varepsilon _{2n}$
.
$\Sigma \varepsilon _{2m}\wedge \varepsilon _{2n}$
.
The second property needed is a certain factorization. Let
be the inclusion of the bottom cell, and let
be the suspension, which is adjoint to the identity map on
![]() $S^{n+1}$
. (This is the same as the map E in the
$S^{n+1}$
. (This is the same as the map E in the
![]() $EHP$
sequence if
$EHP$
sequence if
![]() $n=2m$
and
$n=2m$
and
![]() $p=2$
; the duplication of notation is not ideal, but the context will make clear which is meant.) Note that localized at an odd prime p, the sphere
$p=2$
; the duplication of notation is not ideal, but the context will make clear which is meant.) Note that localized at an odd prime p, the sphere
![]() $S^{2m-1}$
is an H-space, implying that the suspension
$S^{2m-1}$
is an H-space, implying that the suspension
![]() ${{S^{2m-1}}\stackrel {{E}}{\longrightarrow }{\Omega S^{2m}}}$
has a left homotopy inverse.
${{S^{2m-1}}\stackrel {{E}}{\longrightarrow }{\Omega S^{2m}}}$
has a left homotopy inverse.
Lemma 2.4 If p is odd and
![]() $m\geq 1$
, then there is a homotopy commutative diagram
$m\geq 1$
, then there is a homotopy commutative diagram

where r is a left homotopy inverse for E.
Proof Let
![]() $w\colon {{S^{4m-1}}\stackrel {{}}{\longrightarrow }{S^{2m}}}$
be the Whitehead product of the identity map on
$w\colon {{S^{4m-1}}\stackrel {{}}{\longrightarrow }{S^{2m}}}$
be the Whitehead product of the identity map on
![]() $S^{2m}$
with itself. At odd primes, the homotopy fiber of w is
$S^{2m}$
with itself. At odd primes, the homotopy fiber of w is
![]() $S^{2m-1}$
, resulting in a homotopy fibration
$S^{2m-1}$
, resulting in a homotopy fibration
Notice that
![]() $\partial \circ E$
is degree one in homology and so is homotopic to the identity map. Therefore, the composite
$\partial \circ E$
is degree one in homology and so is homotopic to the identity map. Therefore, the composite
is a homotopy equivalence, where
![]() $\mu $
is the standard loop multiplication. Consider the diagram
$\mu $
is the standard loop multiplication. Consider the diagram

where
![]() $\pi _{1}$
is the projection onto the first factor and
$\pi _{1}$
is the projection onto the first factor and
![]() $j_{1}$
is the inclusion of the first factor. The left square homotopy commutes since
$j_{1}$
is the inclusion of the first factor. The left square homotopy commutes since
![]() $\epsilon _{2m}\circ w$
is null homotopic (as
$\epsilon _{2m}\circ w$
is null homotopic (as
![]() $J_{2}(S^{2m})$
is the homotopy cofiber of w and p odd implies
$J_{2}(S^{2m})$
is the homotopy cofiber of w and p odd implies
![]() $p-1\geq 2$
). The right square homotopy commutes since
$p-1\geq 2$
). The right square homotopy commutes since
![]() $\Omega \epsilon _{2m}$
is an H-map. The upper row is the homotopy equivalence e, and the bottom row is homotopic to
$\Omega \epsilon _{2m}$
is an H-map. The upper row is the homotopy equivalence e, and the bottom row is homotopic to
![]() $\varepsilon _{2m}$
. The homotopy commutativity of the diagram therefore implies that
$\varepsilon _{2m}$
. The homotopy commutativity of the diagram therefore implies that
![]() $\Omega \epsilon _{2m}\circ e\simeq \varepsilon _{2m}\circ \pi _{1}$
. Now, precompose this diagram with the map
$\Omega \epsilon _{2m}\circ e\simeq \varepsilon _{2m}\circ \pi _{1}$
. Now, precompose this diagram with the map
![]() ${{\Omega S^{2m}}\stackrel {{e^{-1}}}{\longrightarrow }{S^{2m-1}\times \Omega S^{4m-1}}} $
to obtain
${{\Omega S^{2m}}\stackrel {{e^{-1}}}{\longrightarrow }{S^{2m-1}\times \Omega S^{4m-1}}} $
to obtain
![]() $\Omega \epsilon _{2m}\simeq \varepsilon _{2m}\circ \pi _{1}\circ e^{-1}$
. Define
$\Omega \epsilon _{2m}\simeq \varepsilon _{2m}\circ \pi _{1}\circ e^{-1}$
. Define
![]() $r\colon {{\Omega S^{2m}}\stackrel {{}}{\longrightarrow }{S^{2m-1}}}$
by
$r\colon {{\Omega S^{2m}}\stackrel {{}}{\longrightarrow }{S^{2m-1}}}$
by
![]() $r=\pi _{1}\circ e^{-1}$
. Then
$r=\pi _{1}\circ e^{-1}$
. Then
![]() $\Omega \epsilon \simeq \varepsilon _{2m}\circ r$
, giving the homotopy commutative square in the statement of the lemma. Also, observe that r is degree one in
$\Omega \epsilon \simeq \varepsilon _{2m}\circ r$
, giving the homotopy commutative square in the statement of the lemma. Also, observe that r is degree one in
![]() $H_{2m-1}(\ \ )$
, so
$H_{2m-1}(\ \ )$
, so
![]() $r\circ E$
is the identity map in homology and therefore is homotopic to the identity map.
$r\circ E$
is the identity map in homology and therefore is homotopic to the identity map.
Let
![]() ${\mathbb {Z}_{(p)}}$
be the integers localized at p. The third property needed is an approximation of the Eilenberg–MacLane space
${\mathbb {Z}_{(p)}}$
be the integers localized at p. The third property needed is an approximation of the Eilenberg–MacLane space
![]() $K({\mathbb {Z}_{(p)}},2m)$
by
$K({\mathbb {Z}_{(p)}},2m)$
by
![]() $J_{p-1}(S^{2m})$
. Let
$J_{p-1}(S^{2m})$
. Let
![]() ${{S^{2m+1}}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m+1)}}$
be the inclusion of the bottom cell. Loop to obtain a map
${{S^{2m+1}}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m+1)}}$
be the inclusion of the bottom cell. Loop to obtain a map
![]() ${{\Omega S^{2m+1}}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m)}}$
. Let
${{\Omega S^{2m+1}}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m)}}$
. Let
![]() $\varphi $
be the composite
$\varphi $
be the composite
As the homotopy fiber of E is
![]() $\Omega ^{2} S^{2mp+1}$
, the map E induces an isomorphism on
$\Omega ^{2} S^{2mp+1}$
, the map E induces an isomorphism on
![]() $\pi _{n}$
for
$\pi _{n}$
for
![]() $n\leq 2mp-2$
. On the other hand, the first nontrivial torsion homotopy group of
$n\leq 2mp-2$
. On the other hand, the first nontrivial torsion homotopy group of
![]() $\Omega S^{2m+1}$
occurs in dimension
$\Omega S^{2m+1}$
occurs in dimension
![]() $2p-3+2m$
, so the right map in (2.1) induces an isomorphism on
$2p-3+2m$
, so the right map in (2.1) induces an isomorphism on
![]() $\pi _{n}$
for
$\pi _{n}$
for
![]() $n<2p-3+2m$
. It is straightforward to see that
$n<2p-3+2m$
. It is straightforward to see that
![]() $2mp-2\geq 2p-3+2m$
for all
$2mp-2\geq 2p-3+2m$
for all
![]() $m\geq 2$
. Therefore,
$m\geq 2$
. Therefore,
![]() $\varphi $
induces an isomorphism on
$\varphi $
induces an isomorphism on
![]() $\pi _{n}$
for all
$\pi _{n}$
for all
![]() $n<2p-3+2m$
. Consequently, we obtain the following.
$n<2p-3+2m$
. Consequently, we obtain the following.
Lemma 2.5 Let X be a
![]() $CW$
-complex of dimension n, and suppose that there is a map
$CW$
-complex of dimension n, and suppose that there is a map
![]() ${{X}\stackrel {{r}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m)}}$
. If
${{X}\stackrel {{r}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m)}}$
. If
![]() $n<2p-3+2m$
, then there is a lift
$n<2p-3+2m$
, then there is a lift

for some map
![]() $\overline {r}$
.
$\overline {r}$
.
This completes the preliminaries needed for the James construction, but it is useful to record here the companion approximation of the Eilenberg–MacLane space
![]() $K({\mathbb {Z}_{(p)}},2m+1)$
by
$K({\mathbb {Z}_{(p)}},2m+1)$
by
![]() $S^{2m+1}$
. Rationally, the inclusion
$S^{2m+1}$
. Rationally, the inclusion
![]() ${{S^{2m+1}}\stackrel {{}}{\longrightarrow }{K(\mathbb {Q},2m+1)}}$
of the bottom cell is a homotopy equivalence. Localized at a prime p, the least nonvanishing torsion homotopy group of
${{S^{2m+1}}\stackrel {{}}{\longrightarrow }{K(\mathbb {Q},2m+1)}}$
of the bottom cell is a homotopy equivalence. Localized at a prime p, the least nonvanishing torsion homotopy group of
![]() $S^{2m+1}$
occurs in dimension
$S^{2m+1}$
occurs in dimension
![]() $2p-2+2m$
. Therefore, if
$2p-2+2m$
. Therefore, if
![]() $2p-2+2m>n$
, then the inclusion
$2p-2+2m>n$
, then the inclusion
![]() ${{S^{2m+1}}\stackrel {{}}{\longrightarrow }{K(\mathbb {Z}_{(p)},2m+1)}}$
of the bottom cell induces an isomorphism on
${{S^{2m+1}}\stackrel {{}}{\longrightarrow }{K(\mathbb {Z}_{(p)},2m+1)}}$
of the bottom cell induces an isomorphism on
![]() $\pi _{m}$
for
$\pi _{m}$
for
![]() $m\leq n$
. Consequently, we obtain the following.
$m\leq n$
. Consequently, we obtain the following.
Lemma 2.6 Let X be a
![]() $CW$
-complex of dimension n, and suppose that there is a map
$CW$
-complex of dimension n, and suppose that there is a map
![]() ${{X}\stackrel {{r}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m+1)}}$
. If
${{X}\stackrel {{r}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},2m+1)}}$
. If
![]() $n<2p-2+2m$
, then there is a lift
$n<2p-2+2m$
, then there is a lift

for some map
![]() $\overline {r}$
.
$\overline {r}$
.
3 Conditions for the non-existence of an exponent at p
In this section, an elementary approach involving Hurewicz images and localization is described that leads to conditions implying that a space has no exponent at a given prime p. Specific application to connected sums of Poincaré Duality complexes will be in the next section.
We begin with a preliminary result proved by Ganea [Reference GaneaG].
Lemma 3.1 Let X and Y be path-connected spaces. Including the wedge into the product, there is a homotopy fibration
that splits after looping to give a homotopy equivalence
Further, the fibration and the homotopy equivalence are natural for maps
![]() ${{X}\stackrel {{}}{\longrightarrow }{X'}}$
and
${{X}\stackrel {{}}{\longrightarrow }{X'}}$
and
![]() ${{Y}\stackrel {{}}{\longrightarrow }{Y'}}$
.
${{Y}\stackrel {{}}{\longrightarrow }{Y'}}$
.
Let X be a simply connected
![]() $CW$
-complex of dimension
$CW$
-complex of dimension
![]() $m\geq 2$
. If X has dimension
$m\geq 2$
. If X has dimension
![]() $2$
, then it is homotopy equivalent to
$2$
, then it is homotopy equivalent to
![]() $\bigvee _{i=1}^{d} S^{2}$
for some
$\bigvee _{i=1}^{d} S^{2}$
for some
![]() $d\geq 1$
(assuming that X is not trivial). If
$d\geq 1$
(assuming that X is not trivial). If
![]() $d=1$
, then
$d=1$
, then
![]() $X=S^{2}$
is elliptic and has an exponent at every prime p. If
$X=S^{2}$
is elliptic and has an exponent at every prime p. If
![]() $d>1$
, then X is a wedge of at least two simply connected spheres, implying that it is hyperbolic and has no exponent at any prime p. So, from here on, assume that
$d>1$
, then X is a wedge of at least two simply connected spheres, implying that it is hyperbolic and has no exponent at any prime p. So, from here on, assume that
![]() $n\geq 3$
.
$n\geq 3$
.
Localize at a prime p. Suppose that there are maps
whose Hurewicz images a and b, respectively, generate distinct
![]() ${\mathbb {Z}_{(p)}}$
summands in
${\mathbb {Z}_{(p)}}$
summands in
![]() $H_{k}(X;{\mathbb {Z}_{(p)}})$
and
$H_{k}(X;{\mathbb {Z}_{(p)}})$
and
![]() $H_{\ell }(X;{\mathbb {Z}_{(p)}})$
. The universal coefficient theorem implies that a and b have dual classes
$H_{\ell }(X;{\mathbb {Z}_{(p)}})$
. The universal coefficient theorem implies that a and b have dual classes
![]() $\bar {a}\in H^{k}(X;{\mathbb {Z}_{(p)}})$
and
$\bar {a}\in H^{k}(X;{\mathbb {Z}_{(p)}})$
and
![]() $\bar {b}\in H^{\ell }(X;{\mathbb {Z}_{(p)}})$
. The cohomology classes
$\bar {b}\in H^{\ell }(X;{\mathbb {Z}_{(p)}})$
. The cohomology classes
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
are represented by maps
$\bar {b}$
are represented by maps
Thus, the composites
are homotopic to the inclusions of the bottom cells.
Now, an adjustment is made. Let
![]() $L(k)=S^{k}$
if k is odd, and let
$L(k)=S^{k}$
if k is odd, and let
![]() $L(k)=J_{p-1}(S^{k})$
if k is even; let
$L(k)=J_{p-1}(S^{k})$
if k is even; let
![]() $L(\ell )=S^{\ell }$
if
$L(\ell )=S^{\ell }$
if
![]() $\ell $
is odd, and let
$\ell $
is odd, and let
![]() $L(\ell )=J_{p-1}(S^{\ell })$
if
$L(\ell )=J_{p-1}(S^{\ell })$
if
![]() $\ell $
is even. Suppose that
$\ell $
is even. Suppose that
![]() $p>\max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2}\}$
. Then, as X has dimension n, Lemmas 2.5 and 2.6 imply that there are lifts
$p>\max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2}\}$
. Then, as X has dimension n, Lemmas 2.5 and 2.6 imply that there are lifts

for some maps
![]() $\overline {r}$
and
$\overline {r}$
and
![]() $\overline {s}$
. Observe that the composites
$\overline {s}$
. Observe that the composites
are homotopic to the identity map when k or
![]() $\ell $
is odd and homotopic to the inclusion of the bottom cell when k or
$\ell $
is odd and homotopic to the inclusion of the bottom cell when k or
![]() $\ell $
is even.
$\ell $
is even.
Since r and s represent cohomology classes dual to the Hurewicz images generated by i and j, we have
![]() $r\circ j$
and
$r\circ j$
and
![]() $s\circ i$
null homotopic. Therefore,
$s\circ i$
null homotopic. Therefore,
![]() $\overline {r}\circ j$
and
$\overline {r}\circ j$
and
![]() $\overline {s}\circ i$
are also null homotopic since the approximations
$\overline {s}\circ i$
are also null homotopic since the approximations
![]() $L(k)$
and
$L(k)$
and
![]() $L(\ell )$
to the Eilenberg–MacLane spaces
$L(\ell )$
to the Eilenberg–MacLane spaces
![]() $K({\mathbb {Z}_{(p)}},k)$
and
$K({\mathbb {Z}_{(p)}},k)$
and
![]() $K({\mathbb {Z}_{(p)}},\ell )$
induce isomorphisms on
$K({\mathbb {Z}_{(p)}},\ell )$
induce isomorphisms on
![]() $\pi _{m}$
for
$\pi _{m}$
for
![]() $m\leq n$
. Suppose that there is a lift
$m\leq n$
. Suppose that there is a lift

In general, given maps
![]() $f\colon {{A}\stackrel {{}}{\longrightarrow }{Z}}$
and
$f\colon {{A}\stackrel {{}}{\longrightarrow }{Z}}$
and
![]() $g\colon {{B}\stackrel {{}}{\longrightarrow }{Z}}$
, let
$g\colon {{B}\stackrel {{}}{\longrightarrow }{Z}}$
, let
![]() $f\perp g\colon {{A\vee B}\stackrel {{}}{\longrightarrow }{Z}}$
be the map uniquely determined by having its restrictions to A and B being f and g, respectively. Then, from (3.2), we obtain a composite
$f\perp g\colon {{A\vee B}\stackrel {{}}{\longrightarrow }{Z}}$
be the map uniquely determined by having its restrictions to A and B being f and g, respectively. Then, from (3.2), we obtain a composite
that is homotopic to
![]() $\alpha \vee \beta $
.
$\alpha \vee \beta $
.
Composing each map in (3.3) with the inclusion
![]() ${{L(k)\vee L(\ell )}\stackrel {{}}{\longrightarrow }{L(k)\times L(\ell )}} $
and taking homotopy fibers gives a homotopy fibration diagram
${{L(k)\vee L(\ell )}\stackrel {{}}{\longrightarrow }{L(k)\times L(\ell )}} $
and taking homotopy fibers gives a homotopy fibration diagram

where the homotopy fibration in the right column is from Lemma 3.1 and the fibration diagram defines the spaces Y and Z.
Lemma 3.2 There is a homotopy commutative diagram

Proof Observe that the middle row of (3.4) is homotopic to
![]() $\alpha \vee \beta $
. Thus, Z is the homotopy pullback of
$\alpha \vee \beta $
. Thus, Z is the homotopy pullback of
![]() $\alpha \vee \beta $
and
$\alpha \vee \beta $
and
![]() ${{\Sigma \Omega L(k)\wedge \Omega L(\ell )}\stackrel {{}}{\longrightarrow }{L(k)\vee L(\ell )}}$
. On the other hand, the naturality of Lemma 3.1 implies that there is a homotopy fibration diagram
${{\Sigma \Omega L(k)\wedge \Omega L(\ell )}\stackrel {{}}{\longrightarrow }{L(k)\vee L(\ell )}}$
. On the other hand, the naturality of Lemma 3.1 implies that there is a homotopy fibration diagram

The homotopy commutativity of the upper square therefore implies that there is a pullback map
![]() ${{\Sigma \Omega S^{k}\wedge \Omega S^{\ell }}\stackrel {{}}{\longrightarrow }{Z}}$
such that the composite
${{\Sigma \Omega S^{k}\wedge \Omega S^{\ell }}\stackrel {{}}{\longrightarrow }{Z}}$
such that the composite
![]() ${\Sigma \Omega S^{k}\wedge \Omega S^{\ell }}\stackrel {{}}{\longrightarrow }{Z}\stackrel {{}}{\longrightarrow } {Y}\stackrel {}{\longrightarrow } {{\Sigma \Omega L(k)\wedge \Omega L(\ell )}}$
is homotopic to
${\Sigma \Omega S^{k}\wedge \Omega S^{\ell }}\stackrel {{}}{\longrightarrow }{Z}\stackrel {{}}{\longrightarrow } {Y}\stackrel {}{\longrightarrow } {{\Sigma \Omega L(k)\wedge \Omega L(\ell )}}$
is homotopic to
![]() $\Sigma \Omega \alpha \wedge \Omega \beta $
.
$\Sigma \Omega \alpha \wedge \Omega \beta $
.
Next, consider the diagram

The upper-left triangle homotopy commutes by the preceding paragraph. The lower-left square homotopy commutes by (3.4). By Lemma 3.1, the map
![]() ${\Sigma \Omega L(k)\wedge \Omega L(\ell )} \stackrel {{}}{\longrightarrow }{L(k)\vee L(\ell )} $
has a left homotopy inverse after looping. Using this left homotopy inverse, the lower-right triangle homotopy commutes. The outer perimeter of this diagram then gives the homotopy commutative diagram asserted by the lemma.
${\Sigma \Omega L(k)\wedge \Omega L(\ell )} \stackrel {{}}{\longrightarrow }{L(k)\vee L(\ell )} $
has a left homotopy inverse after looping. Using this left homotopy inverse, the lower-right triangle homotopy commutes. The outer perimeter of this diagram then gives the homotopy commutative diagram asserted by the lemma.
Next, a full or partial left homotopy inverse of
![]() $\Sigma \Omega \alpha \wedge \Omega \beta $
is considered.
$\Sigma \Omega \alpha \wedge \Omega \beta $
is considered.
Lemma 3.3 The following hold:
-
(a) If k and
 $\ell $
are both odd, then
$\ell $
are both odd, then
 $\Sigma \Omega \alpha \wedge \Omega \beta $
has a left homotopy inverse.
$\Sigma \Omega \alpha \wedge \Omega \beta $
has a left homotopy inverse. -
(b) If k is odd and
 $\ell $
is even, then the composite has a left homotopy inverse.
$\ell $
is even, then the composite has a left homotopy inverse.
-
(c) If k is even and
 $\ell $
is odd, then the composite has a left homotopy inverse.
$\ell $
is odd, then the composite has a left homotopy inverse.
Proof If k and
![]() $\ell $
are both odd, then, by definition,
$\ell $
are both odd, then, by definition,
![]() $L(k)= S^{k}$
and
$L(k)= S^{k}$
and
![]() $L(\ell )=S^{\ell }$
and both
$L(\ell )=S^{\ell }$
and both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are homotopic to the identity maps. This proves part (a).
$\beta $
are homotopic to the identity maps. This proves part (a).
If k is odd and
![]() $\ell $
is even, then, by definition,
$\ell $
is even, then, by definition,
![]() $L(k)=S^{k}$
,
$L(k)=S^{k}$
,
![]() $L(\ell )=J(S^{\ell })$
,
$L(\ell )=J(S^{\ell })$
,
![]() $\alpha $
is homotopic to the identity map, and
$\alpha $
is homotopic to the identity map, and
![]() $\beta $
is homotopic to the inclusion
$\beta $
is homotopic to the inclusion
![]() $\epsilon _{\ell }$
of the bottom cell. Thus, the composite
$\epsilon _{\ell }$
of the bottom cell. Thus, the composite
is homotopic to
By Lemma 2.2,
![]() $\Sigma \varepsilon _{\ell }$
has a left homotopy inverse. Therefore, so does
$\Sigma \varepsilon _{\ell }$
has a left homotopy inverse. Therefore, so does
![]() $\Sigma 1\wedge \varepsilon _{\ell }$
. This proves part (b).
$\Sigma 1\wedge \varepsilon _{\ell }$
. This proves part (b).
The argument for part (c) is the same as for part (b) but with the roles of k and
![]() $\ell $
exchanged.
$\ell $
exchanged.
Collecting what has been done so far gives the following.
Proposition 3.4 Let X be a finite simply connected
![]() $CW$
-complex of dimension
$CW$
-complex of dimension
![]() $n\geq 3$
. Localize at a prime p. Suppose that there are maps
$n\geq 3$
. Localize at a prime p. Suppose that there are maps
![]() ${{S^{k}}\stackrel {{i}}{\longrightarrow }{X}}$
and
${{S^{k}}\stackrel {{i}}{\longrightarrow }{X}}$
and
![]() ${{S^{\ell }}\stackrel {{j}}{\longrightarrow }{X}} $
whose Hurewicz images generate distinct
${{S^{\ell }}\stackrel {{j}}{\longrightarrow }{X}} $
whose Hurewicz images generate distinct
![]() ${\mathbb {Z}_{(p)}}$
summands of
${\mathbb {Z}_{(p)}}$
summands of
![]() $H_{\ast }(X;{\mathbb {Z}_{(p)}})$
and there is a lift as in (3.2). If
$H_{\ast }(X;{\mathbb {Z}_{(p)}})$
and there is a lift as in (3.2). If
![]() $p>\max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2}\}$
and one of k or
$p>\max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2}\}$
and one of k or
![]() $\ell $
is odd, then X is hyperbolic and has no homotopy exponent at p.
$\ell $
is odd, then X is hyperbolic and has no homotopy exponent at p.
Proof Since one of k or
![]() $\ell $
is odd, each of the three cases in Lemma 3.3 implies that there is a countable wedge W of simply connected spheres with the property that the composite
$\ell $
is odd, each of the three cases in Lemma 3.3 implies that there is a countable wedge W of simply connected spheres with the property that the composite ![]() has a left homotopy inverse. Thus, the homotopy commutativity of the diagram in the statement of Lemma 3.3 implies that
has a left homotopy inverse. Thus, the homotopy commutativity of the diagram in the statement of Lemma 3.3 implies that
![]() $\Omega W$
retracts off
$\Omega W$
retracts off
![]() $\Omega X$
. Therefore, as W is hyperbolic and has no exponent at p, the same is true of X.
$\Omega X$
. Therefore, as W is hyperbolic and has no exponent at p, the same is true of X.
The case when both k and
![]() $\ell $
are even is different. In Lemma 3.3, the map
$\ell $
are even is different. In Lemma 3.3, the map
![]() $\Sigma \Omega \alpha \wedge \Omega \beta $
now takes the form
$\Sigma \Omega \alpha \wedge \Omega \beta $
now takes the form ![]() . By Lemma 2.4 applied to both
. By Lemma 2.4 applied to both
![]() $\Omega \epsilon _{k}$
and
$\Omega \epsilon _{k}$
and
![]() $\Omega \epsilon _{\ell }$
, the map
$\Omega \epsilon _{\ell }$
, the map
![]() $\Sigma \Omega \epsilon _{k}\wedge \Omega \epsilon _{\ell }$
factors through
$\Sigma \Omega \epsilon _{k}\wedge \Omega \epsilon _{\ell }$
factors through
![]() $\Sigma S^{k-1}\wedge S^{\ell -1}$
. Thus, only one of the spheres in
$\Sigma S^{k-1}\wedge S^{\ell -1}$
. Thus, only one of the spheres in
![]() $\Sigma \Omega S^{k}\wedge \Omega S^{\ell }$
retracts off
$\Sigma \Omega S^{k}\wedge \Omega S^{\ell }$
retracts off
![]() $\Sigma \Omega J_{p-1}(S^{k})\wedge \Omega J_{p-1}(S^{\ell })$
, whereas at least two are needed for hyperbolicity and no exponent. To go forward in this case, an extra initial hypothesis is necessary.
$\Sigma \Omega J_{p-1}(S^{k})\wedge \Omega J_{p-1}(S^{\ell })$
, whereas at least two are needed for hyperbolicity and no exponent. To go forward in this case, an extra initial hypothesis is necessary.
Assume that there is another map
whose Hurewicz image
![]() $b'$
generates a
$b'$
generates a
![]() ${\mathbb {Z}_{(p)}}$
summand in
${\mathbb {Z}_{(p)}}$
summand in
![]() $H_{\ell '}(X;{\mathbb {Z}_{(p)}})$
that is distinct from those generated by a and b. The dual class
$H_{\ell '}(X;{\mathbb {Z}_{(p)}})$
that is distinct from those generated by a and b. The dual class
![]() $\overline {b'}\in H^{\ell '}(X;{\mathbb {Z}_{(p)}})$
is represented by a map
$\overline {b'}\in H^{\ell '}(X;{\mathbb {Z}_{(p)}})$
is represented by a map
If
![]() $\ell '$
is odd, then we may replace
$\ell '$
is odd, then we may replace
![]() $\ell $
by
$\ell $
by
![]() $\ell '$
in Proposition 3.4 and we are done. So assume that
$\ell '$
in Proposition 3.4 and we are done. So assume that
![]() $\ell '$
is even. If
$\ell '$
is even. If
![]() $p>\frac {n-\ell '+3}{2}$
, then Lemma 2.5 implies that
$p>\frac {n-\ell '+3}{2}$
, then Lemma 2.5 implies that
![]() $s'$
factors as a composite
$s'$
factors as a composite
![]() $ {{X}\stackrel {{\overline {s'}}}{\longrightarrow }{J_{p-1} (S^{\ell '})}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell ')}} $
for some map
$ {{X}\stackrel {{\overline {s'}}}{\longrightarrow }{J_{p-1} (S^{\ell '})}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell ')}} $
for some map
![]() $\overline {s'}$
. Observe that the composite
$\overline {s'}$
. Observe that the composite
![]() ${{S^{\ell '}}\stackrel {{}}{\longrightarrow }{X}\stackrel {{\overline {s'}}}{\longrightarrow }{J_{p-1}(S^{\ell '})}} $
is homotopic to the inclusion of the bottom cell. Define
${{S^{\ell '}}\stackrel {{}}{\longrightarrow }{X}\stackrel {{\overline {s'}}}{\longrightarrow }{J_{p-1}(S^{\ell '})}} $
is homotopic to the inclusion of the bottom cell. Define
![]() $\gamma $
by the composite
$\gamma $
by the composite
Observe that
![]() $\gamma $
is homotopic to
$\gamma $
is homotopic to
![]() $(j_{1}\circ \epsilon _{\ell })\perp (j_{2}\circ \epsilon _{\ell '})$
, where
$(j_{1}\circ \epsilon _{\ell })\perp (j_{2}\circ \epsilon _{\ell '})$
, where
![]() $j_{1}$
and
$j_{1}$
and
![]() $j_{2}$
are the inclusions of the first and second factors into
$j_{2}$
are the inclusions of the first and second factors into
![]() $J_{p-1}(S^{\ell })\times J_{p-1}(S^{\ell '})$
.
$J_{p-1}(S^{\ell })\times J_{p-1}(S^{\ell '})$
.
In place of (3.2), suppose that there is a lift

Then the composite
is homotopic to
![]() $\alpha \vee \gamma $
. Now, replace j and
$\alpha \vee \gamma $
. Now, replace j and
![]() $L(\ell )$
in (3.4) with
$L(\ell )$
in (3.4) with
![]() $j\perp j'$
and
$j\perp j'$
and
![]() $L(\ell )\times L(\ell ')$
and argue as in Lemma 3.2 to obtain the following.
$L(\ell )\times L(\ell ')$
and argue as in Lemma 3.2 to obtain the following.
Lemma 3.5 There is a homotopy commutative diagram

Lemma 3.6 The composite

has a left homotopy inverse.
Proof By their definitions,
![]() $\overline {\alpha }$
is homotopic to
$\overline {\alpha }$
is homotopic to
![]() $\epsilon _{k}$
and
$\epsilon _{k}$
and
![]() $\overline {\gamma }$
is homotopic to
$\overline {\gamma }$
is homotopic to
![]() $(j_{1}\circ \epsilon _{\ell })\perp (j_{2}\circ \epsilon _{\ell '})$
. Thus,
$(j_{1}\circ \epsilon _{\ell })\perp (j_{2}\circ \epsilon _{\ell '})$
. Thus,
![]() $\Omega \alpha \circ E\simeq \varepsilon _{k}$
and
$\Omega \alpha \circ E\simeq \varepsilon _{k}$
and
![]() $\Omega \gamma \circ E\simeq (\Omega j_{1}\circ \varepsilon _{\ell })\perp (\Omega j_{1}\circ \varepsilon _{\ell '})$
. By Lemma 2.2, each of
$\Omega \gamma \circ E\simeq (\Omega j_{1}\circ \varepsilon _{\ell })\perp (\Omega j_{1}\circ \varepsilon _{\ell '})$
. By Lemma 2.2, each of
![]() $\Sigma \varepsilon _{k}$
,
$\Sigma \varepsilon _{k}$
,
![]() $\Sigma \varepsilon _{\ell }$
, and
$\Sigma \varepsilon _{\ell }$
, and
![]() $\Sigma \varepsilon _{\ell '}$
has a left homotopy inverse, denoted by
$\Sigma \varepsilon _{\ell '}$
has a left homotopy inverse, denoted by
![]() $\delta _{k}$
,
$\delta _{k}$
,
![]() $\delta _{\ell }$
, and
$\delta _{\ell }$
, and
![]() $\delta _{\ell '}$
respectively. A left homotopy inverse of
$\delta _{\ell '}$
respectively. A left homotopy inverse of
![]() $(\Sigma \Omega \alpha \wedge \Omega \beta )\circ (\Sigma E\wedge E)$
is then given by the composite
$(\Sigma \Omega \alpha \wedge \Omega \beta )\circ (\Sigma E\wedge E)$
is then given by the composite

where t comes from the splitting of
![]() $\Sigma (A\times B)$
as
$\Sigma (A\times B)$
as
![]() $\Sigma A\vee \Sigma B\vee (\Sigma A\wedge B)$
.
$\Sigma A\vee \Sigma B\vee (\Sigma A\wedge B)$
.
The analogue of Proposition 3.4 in this case is the following.
Proposition 3.7 Let X be a finite simply connected
![]() $CW$
-complex of dimension
$CW$
-complex of dimension
![]() $n\geq 3$
. Localize at a prime p. Suppose that there are maps
$n\geq 3$
. Localize at a prime p. Suppose that there are maps
![]() ${{S^{k}}\stackrel {{i}}{\longrightarrow }{X}}$
,
${{S^{k}}\stackrel {{i}}{\longrightarrow }{X}}$
,
![]() ${{S^{\ell }}\stackrel {{j}}{\longrightarrow }{X}}$
and
${{S^{\ell }}\stackrel {{j}}{\longrightarrow }{X}}$
and
![]() ${{S^{\ell '}}\stackrel {{j'}}{\longrightarrow }{X}}$
whose Hurewicz images generate distinct
${{S^{\ell '}}\stackrel {{j'}}{\longrightarrow }{X}}$
whose Hurewicz images generate distinct
![]() ${\mathbb {Z}_{(p)}}$
summands of
${\mathbb {Z}_{(p)}}$
summands of
![]() $H_{\ast }(X;{\mathbb {Z}_{(p)}})$
and there is a lift as in (3.5). If
$H_{\ast }(X;{\mathbb {Z}_{(p)}})$
and there is a lift as in (3.5). If
![]() $p>\max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2},\frac {n-\ell '+3}{2}\}$
and each of k,
$p>\max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2},\frac {n-\ell '+3}{2}\}$
and each of k,
![]() $\ell $
, and
$\ell $
, and
![]() $\ell '$
is even, then X is hyperbolic and has no homotopy exponent at p.
$\ell '$
is even, then X is hyperbolic and has no homotopy exponent at p.
4 Moore’s conjecture for connected sums
Let M and N be simply connected, closed, orientable n-dimensional Poincaré duality spaces. If
![]() $\overline {M}$
and
$\overline {M}$
and
![]() $\overline {N}$
are the
$\overline {N}$
are the
![]() $(n-1)$
-skeletons of M and N, respectively, there are homotopy cofibrations
$(n-1)$
-skeletons of M and N, respectively, there are homotopy cofibrations
where f and g attach the n-cell to M and N. Geometrically, the connected sum
![]() $M\# N$
is obtained by cutting a small n-disk from each of M and N and then gluing together along the boundary of the disk. Topologically, this implies that the
$M\# N$
is obtained by cutting a small n-disk from each of M and N and then gluing together along the boundary of the disk. Topologically, this implies that the
![]() $(n-1)$
-skeleton of
$(n-1)$
-skeleton of
![]() $M\# N$
is
$M\# N$
is
![]() $\overline {M}\vee \overline {N}$
and there is a homotopy cofibration
$\overline {M}\vee \overline {N}$
and there is a homotopy cofibration
where
![]() $f+g$
is the composite
$f+g$
is the composite
![]() ${{S^{n-1}}\stackrel {{\sigma }}{\longrightarrow }{S^{n-1}\vee S^{n-1}}\stackrel {{f\vee g}}{\longrightarrow }{\overline {M}\vee \overline {N}}} $
, with
${{S^{n-1}}\stackrel {{\sigma }}{\longrightarrow }{S^{n-1}\vee S^{n-1}}\stackrel {{f\vee g}}{\longrightarrow }{\overline {M}\vee \overline {N}}} $
, with
![]() $\sigma $
being the standard comultiplication. Collapsing the “collar” of the connected sum – the boundary of the n-disk along which the two were glued – gives a quotient map
$\sigma $
being the standard comultiplication. Collapsing the “collar” of the connected sum – the boundary of the n-disk along which the two were glued – gives a quotient map
Proof of Theorem 1.2
By hypothesis, M and N are simply connected and not rationally homotopy equivalent to
![]() $S^{n}$
. This implies that if the rational connectivities of M and N are
$S^{n}$
. This implies that if the rational connectivities of M and N are
![]() $k-1$
and
$k-1$
and
![]() $\ell -1$
, respectively, then
$\ell -1$
, respectively, then
![]() $2\leq k,\ell <n$
. Therefore, both
$2\leq k,\ell <n$
. Therefore, both
![]() $H_{k}(M;\mathbb {Q})$
and
$H_{k}(M;\mathbb {Q})$
and
![]() $H_{\ell }(N;\mathbb {Q})$
have a
$H_{\ell }(N;\mathbb {Q})$
have a
![]() $\mathbb {Q}$
-summand in the image of the rational Hurewicz homomorphism. This implies that there are maps
$\mathbb {Q}$
-summand in the image of the rational Hurewicz homomorphism. This implies that there are maps
with Hurewicz images
![]() $m_{1}\cdot a\in H_{k}(M;\mathbb {Z})$
and
$m_{1}\cdot a\in H_{k}(M;\mathbb {Z})$
and
![]() $m_{2}\cdot b\in H_{\ell }(M;\mathbb {Z})$
where a and b generate
$m_{2}\cdot b\in H_{\ell }(M;\mathbb {Z})$
where a and b generate
![]() $\mathbb {Z}$
-summands and
$\mathbb {Z}$
-summands and
![]() $m_{1},m_{2}\in \mathbb {Z}$
. Let
$m_{1},m_{2}\in \mathbb {Z}$
. Let
![]() $\mathcal {P}_{1}$
be the set of all primes that divide either
$\mathcal {P}_{1}$
be the set of all primes that divide either
![]() $m_{1}$
or
$m_{1}$
or
![]() $m_{2}$
, let
$m_{2}$
, let
![]() $\mathcal {P}_{2}$
be the set of all primes
$\mathcal {P}_{2}$
be the set of all primes
![]() $p\leq \max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2}\}$
, and let
$p\leq \max \{\frac {n-k+3}{2},\frac {n-\ell +3}{2}\}$
, and let
![]() $\mathcal {P}=\mathcal {P}_{1}\cup \mathcal {P}_{2}$
. Note that
$\mathcal {P}=\mathcal {P}_{1}\cup \mathcal {P}_{2}$
. Note that
![]() $\mathcal {P}$
is finite, and possibly empty.
$\mathcal {P}$
is finite, and possibly empty.
Case 1: one of k or
![]() $\ell $
is odd. Localize at a prime
$\ell $
is odd. Localize at a prime
![]() $p\notin \mathcal {P}$
. As
$p\notin \mathcal {P}$
. As
![]() $p\notin \mathcal {P}_{1}$
, the Hurewicz images of both i and j generate
$p\notin \mathcal {P}_{1}$
, the Hurewicz images of both i and j generate
![]() ${\mathbb {Z}_{(p)}}$
-summands of
${\mathbb {Z}_{(p)}}$
-summands of
![]() $H_{k}(M;{\mathbb {Z}_{(p)}})$
and
$H_{k}(M;{\mathbb {Z}_{(p)}})$
and
![]() $H_{\ell }(N;{\mathbb {Z}_{(p)}})$
. If the dual classes in
$H_{\ell }(N;{\mathbb {Z}_{(p)}})$
. If the dual classes in
![]() ${\mathbb {Z}_{(p)}}$
cohomology are represented by maps
${\mathbb {Z}_{(p)}}$
cohomology are represented by maps
![]() $r\colon {{M}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},k)}}$
and
$r\colon {{M}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},k)}}$
and
![]() $s\colon {{N}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell )}} $
, respectively, then as we are localized at
$s\colon {{N}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell )}} $
, respectively, then as we are localized at
![]() $p\notin \mathcal {P}_{2}$
, Lemmas 2.6 and 2.5 imply the maps r and s lift to maps
$p\notin \mathcal {P}_{2}$
, Lemmas 2.6 and 2.5 imply the maps r and s lift to maps
![]() $\overline {r}\colon {{M}\stackrel {{}}{\longrightarrow }{L(k)}}$
and
$\overline {r}\colon {{M}\stackrel {{}}{\longrightarrow }{L(k)}}$
and
![]() $\overline {s}\colon {{N}\stackrel {{}}{\longrightarrow }{L(\ell )}}$
. The composite
$\overline {s}\colon {{N}\stackrel {{}}{\longrightarrow }{L(\ell )}}$
. The composite
is then a lift of
![]() $\overline {r}\times \overline {s}$
as in (3.2). Proposition 3.4 now implies that
$\overline {r}\times \overline {s}$
as in (3.2). Proposition 3.4 now implies that
![]() $M\# N$
is hyperbolic and has no exponent at p.
$M\# N$
is hyperbolic and has no exponent at p.
Case 2: both k and
![]() $\ell $
are even. By hypothesis, there is a second rational Hurewicz image in
$\ell $
are even. By hypothesis, there is a second rational Hurewicz image in
![]() $H_{\ell '}(N;\mathbb {Q})$
that generates a
$H_{\ell '}(N;\mathbb {Q})$
that generates a
![]() $\mathbb {Q}$
-summand independent from the Hurewicz image of j. This implies that there is a map
$\mathbb {Q}$
-summand independent from the Hurewicz image of j. This implies that there is a map
![]() $j'\colon {{S^{\ell '}}\stackrel {{}}{\longrightarrow }{N}}$
with Hurewicz image
$j'\colon {{S^{\ell '}}\stackrel {{}}{\longrightarrow }{N}}$
with Hurewicz image
![]() $m_{2}'b'\in H_{\ell '}(N;\mathbb {Z})$
, where
$m_{2}'b'\in H_{\ell '}(N;\mathbb {Z})$
, where
![]() $b'$
generates a
$b'$
generates a
![]() $\mathbb {Z}$
-summand and
$\mathbb {Z}$
-summand and
![]() $m_{2}'\in \mathbb {Z}$
. Let
$m_{2}'\in \mathbb {Z}$
. Let
![]() $\mathcal {P}_{1}'$
be the set of all primes that divide any one of
$\mathcal {P}_{1}'$
be the set of all primes that divide any one of
![]() $m_{1},m_{2}$
, or
$m_{1},m_{2}$
, or
![]() $m_{2}'$
. Note that
$m_{2}'$
. Note that
![]() $\mathcal {P}_{1}\subseteq \mathcal {P}_{1}'$
. Also, as N is rationally
$\mathcal {P}_{1}\subseteq \mathcal {P}_{1}'$
. Also, as N is rationally
![]() $(\ell -1)$
-connected, we have
$(\ell -1)$
-connected, we have
![]() $\ell '\geq \ell $
, implying that
$\ell '\geq \ell $
, implying that
![]() $\frac {n-\ell '+3}{2}\leq \frac {n-\ell +3}{2}$
, so no adjustment is needed to
$\frac {n-\ell '+3}{2}\leq \frac {n-\ell +3}{2}$
, so no adjustment is needed to
![]() $\mathcal {P}_{2}$
. Let
$\mathcal {P}_{2}$
. Let
![]() $\mathcal {P}'=\mathcal {P}^{\prime }_{1}\cup \mathcal {P}_{2}$
. Localize at
$\mathcal {P}'=\mathcal {P}^{\prime }_{1}\cup \mathcal {P}_{2}$
. Localize at
![]() $p\notin \mathcal {P}'$
. As
$p\notin \mathcal {P}'$
. As
![]() $p\notin \mathcal {P}^{\prime }_{1}$
, the Hurewicz images of i, j, and
$p\notin \mathcal {P}^{\prime }_{1}$
, the Hurewicz images of i, j, and
![]() $j'$
generate
$j'$
generate
![]() ${\mathbb {Z}_{(p)}}$
-summands in
${\mathbb {Z}_{(p)}}$
-summands in
![]() $H_{k}(M;{\mathbb {Z}_{(p)}})$
,
$H_{k}(M;{\mathbb {Z}_{(p)}})$
,
![]() $H_{\ell }(N;{\mathbb {Z}_{(p)}})$
, and
$H_{\ell }(N;{\mathbb {Z}_{(p)}})$
, and
![]() $H_{\ell '}(N;{\mathbb {Z}_{(p)}})$
, respectively. If the dual classes in
$H_{\ell '}(N;{\mathbb {Z}_{(p)}})$
, respectively. If the dual classes in
![]() ${\mathbb {Z}_{(p)}}$
-cohomology are represented by maps
${\mathbb {Z}_{(p)}}$
-cohomology are represented by maps
![]() $r\colon {{M}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},k)}}$
,
$r\colon {{M}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},k)}}$
,
![]() $s\colon {{N}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell )}}$
, and
$s\colon {{N}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell )}}$
, and
![]() $s'\colon {{N}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell ')}}$
, respectively, then as we are localized at
$s'\colon {{N}\stackrel {{}}{\longrightarrow }{K({\mathbb {Z}_{(p)}},\ell ')}}$
, respectively, then as we are localized at
![]() $p\notin \mathcal {P}_{2}$
and each of k,
$p\notin \mathcal {P}_{2}$
and each of k,
![]() $\ell $
, and
$\ell $
, and
![]() $\ell '$
is even, Lemma 2.5 implies that r, s, and
$\ell '$
is even, Lemma 2.5 implies that r, s, and
![]() $s'$
lift to maps
$s'$
lift to maps
![]() $\overline {r}\colon {{M}\stackrel {{}}{\longrightarrow }{J_{p-1}(S^{k})}}$
,
$\overline {r}\colon {{M}\stackrel {{}}{\longrightarrow }{J_{p-1}(S^{k})}}$
,
![]() $\overline {s}\colon {{N}\stackrel {{}}{\longrightarrow }{J_{p-1}(S^{\ell })}}$
, and
$\overline {s}\colon {{N}\stackrel {{}}{\longrightarrow }{J_{p-1}(S^{\ell })}}$
, and
![]() $\overline {s'}\colon {{N}\stackrel {{}}{\longrightarrow }{J_{p-1}(S^{\ell '})}} $
. The composite
$\overline {s'}\colon {{N}\stackrel {{}}{\longrightarrow }{J_{p-1}(S^{\ell '})}} $
. The composite
is then a lift of
![]() $\overline {r}\times (\overline {s}\times \overline {s'})$
as in (3.5). Proposition 3.7 now implies that
$\overline {r}\times (\overline {s}\times \overline {s'})$
as in (3.5). Proposition 3.7 now implies that
![]() $M\# N$
is hyperbolic and has no exponent at p.
$M\# N$
is hyperbolic and has no exponent at p.
5 An integral case
An integral statement holds in the context of Proposition 3.7 when
![]() $k=\ell =\ell '=2$
.
$k=\ell =\ell '=2$
.
Proof of Theorem 1.3
Since M and N are simply connected, the hypotheses on
![]() $H_{2}(M;\mathbb {Z})$
and
$H_{2}(M;\mathbb {Z})$
and
![]() $H_{2}(N;\mathbb {Z})$
imply that there are maps
$H_{2}(N;\mathbb {Z})$
imply that there are maps
whose Hurewicz images generate a
![]() $\mathbb {Z}$
summand in
$\mathbb {Z}$
summand in
![]() $H_{2}(M;\mathbb {Z})$
and distinct
$H_{2}(M;\mathbb {Z})$
and distinct
![]() $\mathbb {Z}$
-summands
$\mathbb {Z}$
-summands
![]() $H_{2}(N;\mathbb {Z})$
. The dual cohomology classes are represented by maps
$H_{2}(N;\mathbb {Z})$
. The dual cohomology classes are represented by maps
respectively. Observe that each of
![]() $r\circ i$
,
$r\circ i$
,
![]() $s\circ j$
, and
$s\circ j$
, and
![]() $s'\circ j'$
is the inclusion of the bottom cell and the composite
$s'\circ j'$
is the inclusion of the bottom cell and the composite
is a lift of
![]() $r\times (s\times s')$
in the manner of (3.5).
$r\times (s\times s')$
in the manner of (3.5).
Define
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
by the composites
$\gamma $
by the composites
Then the analogue of Lemma 3.5 is a factorization of
through
![]() $\Omega (M\# N)$
. As
$\Omega (M\# N)$
. As
![]() $\Omega {\mathbb {C}P^{\infty }}\simeq S^{1}$
, the composite
$\Omega {\mathbb {C}P^{\infty }}\simeq S^{1}$
, the composite
has a left homotopy inverse. Therefore, there is a wedge W of two simply connected spheres retracting off
![]() $\Omega (M\# N)$
, implying that it is hyperbolic and has no exponent at any prime p.
$\Omega (M\# N)$
, implying that it is hyperbolic and has no exponent at any prime p.
6 A generalization to certain pullbacks
This section generalizes the result for connected sums. Let M and N be simply connected, closed, orientable n-dimensional manifolds. There is a map
![]() $\pi \colon {{M\# N}\stackrel {{}}{\longrightarrow }{M}}$
that collapses N to a point. (Equivalently,
$\pi \colon {{M\# N}\stackrel {{}}{\longrightarrow }{M}}$
that collapses N to a point. (Equivalently,
![]() $\pi $
is the composite
$\pi $
is the composite
![]() ${{M\# N}\stackrel {{q}}{\longrightarrow }{M\vee N}\stackrel {{p_{1}}}{\longrightarrow }{M}} $
where
${{M\# N}\stackrel {{q}}{\longrightarrow }{M\vee N}\stackrel {{p_{1}}}{\longrightarrow }{M}} $
where
![]() $p_{1}$
pinches onto the first wedge summand.) Suppose that there is a fibration
$p_{1}$
pinches onto the first wedge summand.) Suppose that there is a fibration
![]() ${{F}\stackrel {{}}{\longrightarrow }{E}\stackrel {{}}{\longrightarrow }{M}} $
. Define the space
${{F}\stackrel {{}}{\longrightarrow }{E}\stackrel {{}}{\longrightarrow }{M}} $
. Define the space
![]() $E_{N}$
as the pullback of
$E_{N}$
as the pullback of
![]() $\pi $
and
$\pi $
and
![]() $\alpha $
, giving a homotopy fibration diagram
$\alpha $
, giving a homotopy fibration diagram

The homotopy type of
![]() $E_{N}$
has attracted attention recently. In [Reference Jeffrey and SelickJS], examples were given to show that
$E_{N}$
has attracted attention recently. In [Reference Jeffrey and SelickJS], examples were given to show that
![]() $E_{N}$
is sometimes a connected sum and sometimes not; in [Reference CheneryC], conditions were given for when
$E_{N}$
is sometimes a connected sum and sometimes not; in [Reference CheneryC], conditions were given for when
![]() $\Omega E_{N}$
has the homotopy type of a looped connected sum (even if
$\Omega E_{N}$
has the homotopy type of a looped connected sum (even if
![]() $E_{N}$
may not be homotopy equivalent to a connected sum itself); and in [Reference Huang and TheriaultHT], conditions were given for when
$E_{N}$
may not be homotopy equivalent to a connected sum itself); and in [Reference Huang and TheriaultHT], conditions were given for when
![]() $E_{N}$
is a connected sum. In this paper, we study
$E_{N}$
is a connected sum. In this paper, we study
![]() $E_{N}$
from the point of view of Moore’s conjecture.
$E_{N}$
from the point of view of Moore’s conjecture.
Proposition 6.1 Define the space
![]() $E_{N}$
as in (6.1). If
$E_{N}$
as in (6.1). If
![]() $M\# N$
satisfies the hypotheses of Theorem 1.2 and some multiple of the map
$M\# N$
satisfies the hypotheses of Theorem 1.2 and some multiple of the map
![]() ${{S^{k}}\stackrel {{}}{\longrightarrow }{M}} $
realizing the rational Hurewicz image for M lifts to E, then
${{S^{k}}\stackrel {{}}{\longrightarrow }{M}} $
realizing the rational Hurewicz image for M lifts to E, then
![]() $E_{N}$
is rationally hyperbolic and has no exponent at all but finitely many primes.
$E_{N}$
is rationally hyperbolic and has no exponent at all but finitely many primes.
Proof By hypothesis, there is a map
![]() $i\colon {{S^{k}}\stackrel {{}}{\longrightarrow }{M}}$
which, rationally, generates a
$i\colon {{S^{k}}\stackrel {{}}{\longrightarrow }{M}}$
which, rationally, generates a
![]() $\mathbb {Q}$
-summand in
$\mathbb {Q}$
-summand in
![]() $H_{k}(M;\mathbb {Q})$
. By hypothesis,
$H_{k}(M;\mathbb {Q})$
. By hypothesis,
![]() $t\cdot i$
lifts to a map
$t\cdot i$
lifts to a map
![]() $\widehat {i}\colon {{S^{k}}\stackrel {{}}{\longrightarrow }{E}} $
. Note that as M is not rationally homotopy equivalent to
$\widehat {i}\colon {{S^{k}}\stackrel {{}}{\longrightarrow }{E}} $
. Note that as M is not rationally homotopy equivalent to
![]() $S^{n}$
, its
$S^{n}$
, its
![]() $(n-1)$
-skeleton
$(n-1)$
-skeleton
![]() $\overline {M}$
is not contractible. Therefore, we may assume
$\overline {M}$
is not contractible. Therefore, we may assume
![]() $k<n$
, implying that i factors through
$k<n$
, implying that i factors through
![]() $\overline {M}$
. Also, denoting the factorization by i, consider the diagram
$\overline {M}$
. Also, denoting the factorization by i, consider the diagram

where
![]() $p_{1}$
is the pinch map onto the first wedge summand and
$p_{1}$
is the pinch map onto the first wedge summand and
![]() $\theta $
will be defined momentarily. The inner square homotopy commutes by the definition of
$\theta $
will be defined momentarily. The inner square homotopy commutes by the definition of
![]() $E_{N}$
as a pullback. Observe that the composite along the left column is homotopic to the composite
$E_{N}$
as a pullback. Observe that the composite along the left column is homotopic to the composite
![]() ${{\overline {M}\vee \overline {N}}\stackrel {{p_{1}}}{\longrightarrow }{\overline {M}}\stackrel {{}}{\longrightarrow }{M}} $
, where again
${{\overline {M}\vee \overline {N}}\stackrel {{p_{1}}}{\longrightarrow }{\overline {M}}\stackrel {{}}{\longrightarrow }{M}} $
, where again
![]() $p_{1}$
is the pinch map onto the first wedge summand. Thus, the composite along the outer perimeter in the clockwise direction is homotopic to
$p_{1}$
is the pinch map onto the first wedge summand. Thus, the composite along the outer perimeter in the clockwise direction is homotopic to
![]() ${{S^{k-1}\vee \overline {N}}\stackrel {{p_{1}}}{\longrightarrow }{S^{k-1}}\stackrel {{t\cdot i}}{\longrightarrow }{M}}$
. Since
${{S^{k-1}\vee \overline {N}}\stackrel {{p_{1}}}{\longrightarrow }{S^{k-1}}\stackrel {{t\cdot i}}{\longrightarrow }{M}}$
. Since
![]() $\widehat {t}$
is a lift of
$\widehat {t}$
is a lift of
![]() $t\cdot i$
, the outer perimeter of the diagram homotopy commutes. This implies that there is a homotopy pullback map
$t\cdot i$
, the outer perimeter of the diagram homotopy commutes. This implies that there is a homotopy pullback map
![]() $\theta $
that makes both the left and upper quadrilaterals homotopy commute.
$\theta $
that makes both the left and upper quadrilaterals homotopy commute.
Now, argue as in the proof of Theorem 1.2 with the composite
![]() ${M\# N}\stackrel {{q}}{\longrightarrow }{M\vee N}\stackrel {{}}{\longrightarrow } {L(k)\vee L(\ell )} $
replaced by
${M\# N}\stackrel {{q}}{\longrightarrow }{M\vee N}\stackrel {{}}{\longrightarrow } {L(k)\vee L(\ell )} $
replaced by
![]() ${E_{N}}\stackrel {{}}{\longrightarrow }{M\# N}\stackrel {{q}}{\longrightarrow }{M\vee N}\stackrel {{}} {\longrightarrow }{L(k)\vee L(\ell )}$
(and similarly for the
${E_{N}}\stackrel {{}}{\longrightarrow }{M\# N}\stackrel {{q}}{\longrightarrow }{M\vee N}\stackrel {{}} {\longrightarrow }{L(k)\vee L(\ell )}$
(and similarly for the
![]() $L(k)\vee (L(\ell )\times L(\ell '))$
variant) to show that
$L(k)\vee (L(\ell )\times L(\ell '))$
variant) to show that
![]() $E_{N}$
is hyperbolic and has no exponent at all but finitely many primes. (In fact, the primes inverted are those for the
$E_{N}$
is hyperbolic and has no exponent at all but finitely many primes. (In fact, the primes inverted are those for the
![]() $M\# N$
case and any additional primes dividing t.)
$M\# N$
case and any additional primes dividing t.)