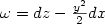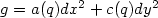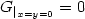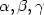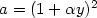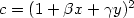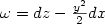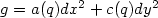Consider a sub-riemannian geometry(U,D,g) where U is a neighborhood of 0 in R3, D is a Martinet type distribution identified to ker ω, ω being the 1-form: $\omega=dz-\frac{y^2}{2}dx$, q=(x,y,z) and g is a metric on D which can be taken in the normal form: $g=a(q)dx^2+c(q)dy^2$, a=1+yF(q), c=1+G(q), $G_{|_{x=y=0}}=0$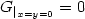. In a previous article we analyze the flat case: a=c=1; we describe the conjugate and cut loci, the sphere and the wave front. The objectif of this article is to provide a geometric and computational framework to analyze the general case. This frame is obtained by analysing three one parameter deformations of the flat case which clarify the role of the three parameters $\alpha,\beta,\gamma$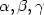 in the gradated normal form of order 0 where: $a=(1+\alpha y)^2$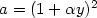, $c=(1+\beta x+\gamma y)^2$. 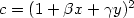More generally this analysis provides an explanation of the role of abnormal minimizers in SR-geometry.