Published online by Cambridge University Press: 15 August 2002
Consider a sub-riemannian geometry(U,D,g) where
U is a neighborhood of 0 in R3, D is a Martinet type
distribution identified to ker ω, ω being the 1-form: $\omega=dz-\frac{y^2}{2}dx$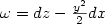 , q=(x,y,z) and
g is a metric on D which can be taken in the normal
form: $g=a(q)dx^2+c(q)dy^2$
, q=(x,y,z) and
g is a metric on D which can be taken in the normal
form: $g=a(q)dx^2+c(q)dy^2$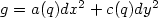 ,
a=1+yF(q), c=1+G(q), $G_{|_{x=y=0}}=0$
,
a=1+yF(q), c=1+G(q), $G_{|_{x=y=0}}=0$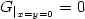 . In a previous article we analyze
the flat case: a=c=1; we describe the conjugate and cut
loci, the sphere and the wave front. The objectif of
this article is to provide a geometric and computational framework
to analyze the general case. This frame is obtained by analysing
three one parameter deformations of the flat case which
clarify the role of the three parameters $\alpha,\beta,\gamma$
. In a previous article we analyze
the flat case: a=c=1; we describe the conjugate and cut
loci, the sphere and the wave front. The objectif of
this article is to provide a geometric and computational framework
to analyze the general case. This frame is obtained by analysing
three one parameter deformations of the flat case which
clarify the role of the three parameters $\alpha,\beta,\gamma$ in
the gradated normal form of order 0 where: $a=(1+\alpha y)^2$
in
the gradated normal form of order 0 where: $a=(1+\alpha y)^2$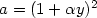 , $c=(1+\beta
x+\gamma y)^2$
, $c=(1+\beta
x+\gamma y)^2$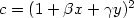 . More generally this analysis provides an explanation of the role
of abnormal minimizers in SR-geometry.
. More generally this analysis provides an explanation of the role
of abnormal minimizers in SR-geometry.