3 results
Equivalence of two descriptions of the ages of alleles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 185-189
- Print publication:
- March 1992
-
- Article
- Export citation
Collision Local Times and Measure-Valued Processes
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 5 / 01 October 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-938
- Print publication:
- 01 October 1991
-
- Article
-
- You have access
- Export citation
The infinitely-many-neutral-alleles diffusion model by ages
-
- Journal:
- Advances in Applied Probability / Volume 22 / Issue 1 / March 1990
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-24
- Print publication:
- March 1990
-
- Article
- Export citation

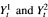 intersect; whereas if
intersect; whereas if 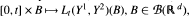 , is concentrated on the set of times and places at which intersections occur. We give a Tanaka-like semimartingale decomposition of
, is concentrated on the set of times and places at which intersections occur. We give a Tanaka-like semimartingale decomposition of 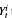 that are uniform in
that are uniform in 