Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T14:26:30.380Z Has data issue: false hasContentIssue false
  • English
  • Français

Collision Local Times and Measure-Valued Processes

Published online by Cambridge University Press:  20 November 2018

Martin T. Barlow ,
Steven N. Evans  and
Edwin A. Perkins
Martin T. Barlow
Affiliation:
Statistical Laboratory, DPMMS, 16 Mill Lane, Cambridge CB2 1SB, United Kingdom
Steven N. Evans
Affiliation:
Department of Statistics, University of California at Berkeley, 367 Evans Hall, Berkeley, CA 94705 USA
Edwin A. Perkins
Affiliation:
Department of Mathematics, University of British Columbia,Vancouver BC V6T1Y4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

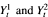We consider two independent Dawson-Watanabe super-Brownian motions, Y1 and Y2. These processes are diffusions taking values in the space of finite measures on ℝd. We show that if d ≤ 5 then with positive probability there exist times t such that the closed supports of intersect; whereas if d > 5 then no such intersections occur. For the case d ≤ 5, we construct a continuous, non-decreasing measure–valued process L(Y1, Y2), the collision local time, such that the measure defined by 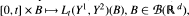, is concentrated on the set of times and places at which intersections occur. We give a Tanaka-like semimartingale decomposition of L(Y1, Y2). We also extend these results to a certain class of coupled measurevalued processes. This extension will be important in a forthcoming paper where we use the tools developed here to construct coupled pairs of measure-valued diffusions with point interactions. In the course of our proofs we obtain smoothness results for the random measures 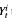that are uniform in t. These theorems use a nonstandard description of Yi and are of independent interest.

Keywords

60G1760G5760J5560H99measure-valued diffusionsuperprocesslocal timeTanaka formulaadditive functionalHausdorff measurenonstandard analysis
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 5 , 01 October 1991 , pp. 897 - 938
Copyright
Copyright © Canadian Mathematical Society 1991

References

Adler, R.J. and Lewin, M. (1990), Super processes on Lp spaces with applications to Tanaka formulae for local times, Stochastic Process Appl., to appear.Google Scholar
Dawson, D.A., Iscoe, I. and Perkins, E.A. (1989), Super-Brownian motion: path properties and hitting probabilities, Probab. Theory Relat. Fields 83, 83–135.Google Scholar
Dawson, D.A. and Perkins, E.A. (1990), Historical processes, Memoirs of the AMS, to appear.Google Scholar
Dynkin, E.B. (1990a), Path processes and historical superprocesses, Prob. Theory Relat. Fields, to appear. (1990b), Superdiffusions and parabolic nonlinear differential equations, preprint.Google Scholar
Dynkin, E.B. (1991), A probabilistic approach to one class of nonlinear differential equations, Prob. Theory Relat. Fields, 89, 89–89.Google Scholar
Ethier, S.N. and Kurtz, T.G. (1986), Markov Processes: Characterization and Convergence. Wiley, New York.Google Scholar
Evans, S.N. and Perkins, E.A. (1991), Absolute continuity results for superprocesses with some applications, Trans. Am. Math. Soc, 325 661–681.Google Scholar
Fitzsimmons, P.J. (1988), Construction and regularity ofmeasure-valued Markov branching processes, Israel J. Math 64, 64–337.Google Scholar
Fitzsimmons, P.J. (1989), Correction and addendum to Construction and regularity of measure-valued Markov branching processes, Israel Journal of Mathematics, to appear.Google Scholar
Hawkes, J. (1978), Measures of Hausdorff type and stable processes, Mathematika 25, 25–202.Google Scholar
Hoover, D.N. and Keisler, H.J. (1984), Adapted probability distributions, Trans. Am. Math. Soc. 286, 286–159.Google Scholar
Knight, F.B. (1981), Essentials ofBrownian Motion and Diffusion. Am. Math. Soc, Providence.Google Scholar
Le Gall, J.F. (1989), Brownian excursions, trees and measure-valued branching processes, Ann. Probab., to appear.Google Scholar
Pazy, A. (1983), Semigroups of linear operators and applications to partial differential equations. Springer-Verlag, Berlin-Heidelberg-New York.Google Scholar
Perkins, E.A. (1988), A space-time property of a class of measure-valued branching diffusions, Trans. Am. Math. Soc. 305, 305–743.Google Scholar
Perkins, E.A. (1989), The Hausdorff measure of the closed support ofsuper-Brownian motion, Ann. Inst. H. Poincaré 25, 25–205.Google Scholar
Perkins, E.A. (1990), Polar sets and multiple points for super-Brownian motion, Ann. Prob. 18, 18–453.Google Scholar
Roelly-Coppoletta, S. (1986), A criterion of convergence of measure-valued processes: application to measure branching processes, Stochastic 17, 17–43.Google Scholar
Taylor, S.J. and Watson, N.A. (1985), A Hausdorff measure classification of polar sets for the heat equation, Math. Proc. Cam. Phil. Soc. 47, 47–325.Google Scholar
Tribe, R. (1989), The behaviour of superprocesses near extinction, Prob. Theory Relat. Fields, to appear.Google Scholar
Walsh, J.B. (1986), An introduction to stochastic partial differential equations. École d'Été de Probabilités de Saint Flour XIV-1984, Lecture Notes in Math. 1180, Springer-Verlag, Berlin-Heidelberg-New York, 265–439.Google Scholar