1 results
An infinite variance solidarity theorem for Markov renewal functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 434-438
- Print publication:
- September 1996
-
- Article
- Export citation

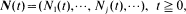 , be a recurrent Markov renewal process and
, be a recurrent Markov renewal process and 