Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pyke, Ronald
1999.
Semi-Markov Models and Applications.
p.
3.
Daley, D. J.
Rolski, T.
and
Vesilo, R.
2007.
Long-Range Dependence in a Cox Process Directed by a Markov Renewal Process.
Journal of Applied Mathematics and Decision Sciences,
Vol. 2007,
Issue. ,
p.
1.
Carpio, K. J. E.
and
Daley, D. J.
2007.
Long-Range Dependence of Markov Chains in Discrete Time on Countable State Space.
Journal of Applied Probability,
Vol. 44,
Issue. 04,
p.
1047.


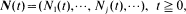 , be a recurrent Markov renewal process and
, be a recurrent Markov renewal process and 