We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we develop a variational method for the Loewner equation in higher dimensions. As a result we obtain a version of Pontryagin’s maximum principle from optimal control theory for the Loewner equation in several complex variables. Based on recent work of Arosio, Bracci, and
Wold, we then apply our version of the Pontryagin maximum principle to obtain first-order necessary
conditions for the extremal mappings for a wide class of extremal problems over the set of normalized
biholomorphic mappings on the unit ball in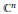 
${{\mathbb{C}}^{n}}$.
