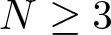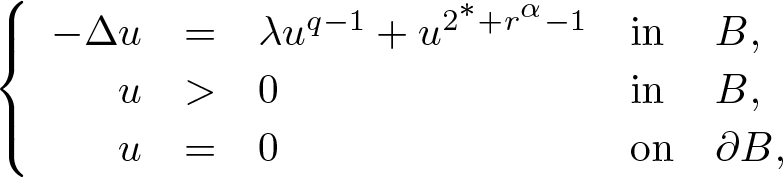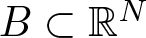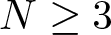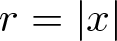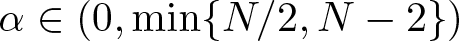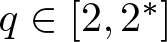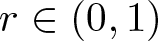2 results
The effect of a perturbation on Brezis-Nirenberg’s problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
-
In this article, we consider some critical Brézis-Nirenberg problems in dimension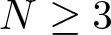
$N \geq 3$ that do not have a solution. We prove that a supercritical perturbation can lead to the existence of a positive solution. More precisely, we consider the equation:where
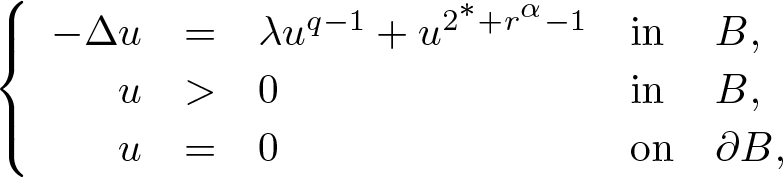\begin{equation*}\left\{\begin{array}{rllll}-\Delta u & = & \lambda u^{q-1} + u^{2^*+ r^\alpha -1} & \mbox{in} & B, \\u & \gt & 0 & \mbox{in} & B, \\u&=&0 & \mbox{on} & \partial B,\\\end{array}\right.\end{equation*}
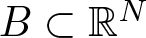$B \subset \mathbb{R}^N$ is a unit ball centred at the origin, 
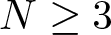$N\geq 3$, 
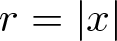$r=\vert x \vert$, 
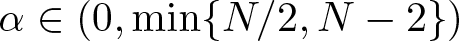$\alpha \in (0,\min\{N/2,N-2\})$, λ is a fixed real parameter and 
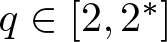$q\in [2,2^*]$. This class of problems can be interpreted as a perturbation of the classical Brézis–Nirenberg problem by the term rα at the exponent, making the problem supercritical when 
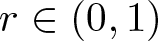$r \in (0,1)$. More specifically, we study the effect of this supercritical perturbation on the existence of solutions. In particular, when N = 3, an interesting and unexpected phenomenon occurs. We obtain the existence of solutions for λ in a range where the Brézis–Nirenberg problem has no solution.
On Triangular Lattice Boltzmann Schemes for Scalar Problems
-
- Journal:
- Communications in Computational Physics / Volume 13 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 649-670
- Print publication:
- March 2013
-
- Article
- Export citation
