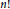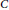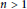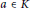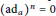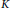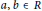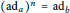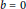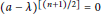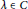1 results
Ad-nilpotent Elements of Semiprime Rings with Involution
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 318-327
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
-
Let R be an 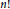n!-torsion free semiprime ring with involution * and with extended centroid 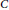C, where 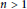n\,>\,1 is a positive integer. We characterize 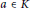a\,\in \,K, the Lie algebra of skew elements in R, satisfying 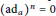{{(\text{a}{{\text{d}}_{a}})}^{n}}\,=\,0 on 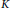K. This generalizes both Martindale and Miers’ theorem and the theorem of Brox et al. In order to prove it we first prove that if 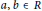a,\,b\,\in \,R satisfy 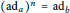{{(\text{a}{{\text{d}}_{a}})}^{n}}\,=\,\text{a}{{\text{d}}_{b}} on R, where either n is even or 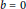b\,=\,0, then 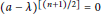{{(a\,-\,\lambda )}^{[(n+1)/2]}}\,=\,0 for some 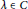\lambda \,\in \,C.
