Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T19:54:20.944Z Has data issue: false hasContentIssue false
  • English
  • Français

Ad-nilpotent Elements of Semiprime Rings with Involution

Published online by Cambridge University Press:  20 November 2018

Tsiu-Kwen Lee
Tsiu-Kwen Lee*
Affiliation:
Department of Mathematics, National Taiwan University, Taipei 106, Taiwan email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $R$ be an 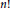$n!$-torsion free semiprime ring with involution $*$ and with extended centroid $C$, where 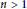$n\,>\,1$ is a positive integer. We characterize 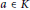$a\,\in \,K$, the Lie algebra of skew elements in $R$, satisfying 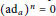${{(\text{a}{{\text{d}}_{a}})}^{n}}\,=\,0$ on 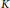$K$. This generalizes both Martindale and Miers’ theorem and the theorem of Brox et al. In order to prove it we first prove that if 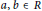$a,\,b\,\in \,R$ satisfy 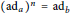${{(\text{a}{{\text{d}}_{a}})}^{n}}\,=\,\text{a}{{\text{d}}_{b}}$ on $R$, where either $n$ is even or 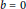$b\,=\,0$, then 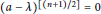${{(a\,-\,\lambda )}^{[(n+1)/2]}}\,=\,0$ for some 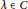$\lambda \,\in \,C$.

Keywords

16N6016W1017B60semiprime ringLie algebraJordan algebrafaithfulf-freeinvolutionskew (symmetric) elementad-nilpotent elementJordan element
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 318 - 327
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Beidar, K. I., Martindale III, W. S., and Mikhalev, A. V., Rings with generalized identities. Monographs and Textbooks in Pure and Applied Mathematics, 196, Marcel Dekker, Inc., New York, 1996 Google Scholar
[2] Beidar, K. I., A. Mikhalev, V., and Salavova, C., Generalized identities and semiprime rings with involution. Math. Z. 178(1981), 37–62. http://dx.doi.Org/10.1007/BF01218370 Google Scholar
[3] Benkart, G., The Lie inner ideal structure of associative rings. J. Algebra 43(1976), 561–584.http://dx.doi.Org/10.101 6/0021-8693(76)90127-7 Google Scholar
[4] Benkart, G., On inner ideals and ad-nilpotent elements ofLie algebras. Trans. Amer. Math. Soc. 232(1977), 61–81.http://dx.doi.org/10.1090/S0002-9947-1977-0466242-6 Google Scholar
[5] Brox, J., Garcia, E. and Lozano, M. G., Jordan algebras at Jordan elements of semiprime rings with involution. J. Algebra 468(2016), 155–181. http://dx.doi.Org/10.1016/j.jalgebra.2016.06.036 Google Scholar
[6] Chuang, C.-L., On nilpotent derivations ofprime rings. Proc. Amer. Math. Soc. 107(1989), 67–71.http://dx.doi.org/10.1090/S0002-9939-1989-0979224-6 Google Scholar
[7] Chuang, C.-L., GPIs having coefficients in Utumi quotient rings. Proc. Amer. Math. Soc. 103(1988), 723–728.http://dx.doi.org/10.1090/S0002-9939-1988-0947646-4 Google Scholar
[8] Chuang, C.-L. and Lee, T.-K., Nilpotent derivations. J. Algebra 287(2005), 381–401.http://dx.doi.Org/10.1016/j.jalgebra.2005.02.010 Google Scholar
[9] Chung, L. O. and Luh, J., Nilpotency of derivatives on an ideal. Proc. Amer. Math. Soc. 90(1984), 211–214. http://dx.doi.org/10.1090/S0002-9939-1984-0727235-3 Google Scholar
[10] Fernandez López, A., Garcia, E., and Lozano, M. G., The Jordan algebras ofa Lie algebra. J. Algebra 308(2007), 164–177.http://dx.doi.Org/10.1016/j.jalgebra.2006.02.035 Google Scholar
[11] Grzeszczuk, P., On nilpotent derivations of semiprime rings. J. Algebra 149(1992), 313–321.http://dx.doi.Org/10.1016/0021-8693(92)90018-H Google Scholar
[12] Harčenko, V. K., Differential identities ofprime rings. (Russian) Algebra i Logika 17(1978), 220-238, 242–243.Google Scholar
[13] Herstein, I. N., Sui commutatori degli anelli semplici. (Italian) Rend. Sem. Mat. Fis. Milano 33(1963), 80–86. http://dx.doi.org/10.1007/BF02923236 Google Scholar
[14] Herstein, I. N., Topics in ring theory. The University of Chicago Press, Chicago, I11.-London 1969.Google Scholar
[15] Jacobson, N., PI-algebras. An introduction. Lecture Notes in Mathematics, 441, Springer-Verlag, Berlin-New York, 1975.Google Scholar
[16] Kovacs, A., Nilpotent derivations. Technion Preprint Series, No. NT-453.Google Scholar
[17] Lee, T.-K., Anti-automorphisms satisfying an Engel condition. Comm. Algebra 45(2017), 4030–4036.http://dx.doi.org/10.1080/00927872.2016.1255894 Google Scholar
[18] Martindale, W. S., III and Miers, C. R., On the iterates of derivations ofprime rings. Pacific J. Math. 104(1983), 179–190.http://dx.doi.org/10.2140/pjm.1983.104.179 Google Scholar
[19] Martindale, W. S., Nilpotent inner derivations ofthe skew elements of prime rings with involution. Canad. J. Math. 43(1991), 1045–1054.http://dx.doi.org/10.4153/CJM-1991-060-2 Google Scholar
[20] Premet, A. A., Lie algebras without strong degeneration. Mat. Sb. (N.S.) 129(171)(1986), 140–153.Google Scholar
[21] Rowen, L., Some results on the center ofa ring with polynomial identity. Bull. Amer. Math. Soc. 79(1973), 219–223.http://dx.doi.org/10.1 090/SOOO2-9904-1973-13162-3 Google Scholar
[22] Tamer Kosan, M., Lee, T.-K., and Zhou, Y., Faithful f-free algebras. Comm. Algebra 41(2013), 638–647.http://dx.doi.org/10.1080/00927872.2011.632798 Google Scholar