We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let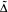 
be the invariant Laplacian on the open unit ball B of Cn and let Xλ denote the set of those f € C2(B) such that 
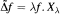counterparts of some known results on X0, i.e. on M-harmonic functions, are investigated here. We distinguish those complex numbers λ for which the real parts of functions in Xλ belongs to Xλ. We distinguish those λ for which the Maximum Modulus Priniple remains true. A kind of weighted Maximum Modulus Principle is presented. As an application, setting α ≥ ½ and λ = 4n2α(α — 1), we obtain a necessary and sufficient condition for a function f in Xλ to be represented as
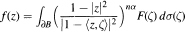
for some F ∊ LP(∂B).
