Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T02:49:28.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Lp Behavior of the Eigenfunctions of the Invariant Laplacian

Published online by Cambridge University Press:  20 November 2018

E. G. Kwon
E. G. Kwon*
Affiliation:
Department of Mathematics Education Andong National University Andong 760-749 Korea
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 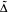be the invariant Laplacian on the open unit ball B of Cn and let Xλ denote the set of those f € C2(B) such that 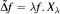counterparts of some known results on X0, i.e. on M-harmonic functions, are investigated here. We distinguish those complex numbers λ for which the real parts of functions in Xλ belongs to Xλ. We distinguish those λ for which the Maximum Modulus Priniple remains true. A kind of weighted Maximum Modulus Principle is presented. As an application, setting α ≥ ½ and λ = 4n2α(α — 1), we obtain a necessary and sufficient condition for a function f in Xλ to be represented as

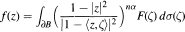
for some F ∊ LP(∂B).

Keywords

31B1031B35Invariant Laplacian
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 36 , Issue 4 , 01 December 1993 , pp. 458 - 465
Copyright
Copyright © Canadian Mathematical Society 1993

References

[K] Kwon, E. G., One radius theorem for the eigenfunctionsofthe invariant Laplacian, Proc. AMS. 116(1992), 27–34.Google Scholar
[KK] Kim, H. O. and Kwon, E. G., M-invariant subspaces of Xλ , Illinois Math, J., to appear.Google Scholar
[R] Rudin, Walter, Function theory in the unit ball ofCn, Springer-Verlag, New York, 1980.Google Scholar
[SI Slater, Lucy John, Generalized hyper geometricfunctions, Cambridge University Press, 1966.Google Scholar