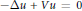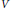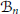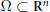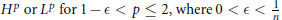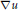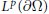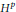We consider the Neumann problem for the Schrödinger equations 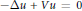-\Delta u\,+\,Vu\,=\,0$-\Delta u\,+\,Vu\,=\,0$, with singular nonnegative potentials 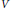V$V$ belonging to the reverse Hölder class 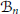{{\mathcal{B}}_{n}}${{\mathcal{B}}_{n}}$ , in a connected Lipschitz domain 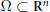\Omega \,\subset \,{{\text{R}}^{n}}$\Omega \,\subset \,{{\text{R}}^{n}}$ . Given boundary data g$g$ in 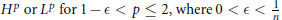{{H}^{p}}\text{or}\,{{L}^{p}}\,\text{for}\,\text{1}-\in \,<\,p\,\le \,2,\text{where}\,\text{0}<\in <\frac{1}{n}${{H}^{p}}\text{or}\,{{L}^{p}}\,\text{for}\,\text{1}-\in \,<\,p\,\le \,2,\text{where}\,\text{0}<\in <\frac{1}{n}$ , it is shown that there is a unique solution, u$u$, that solves the Neumann problem for the given data and such that the nontangential maximal function of 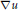\nabla u$\nabla u$ is in 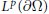{{L}^{p}}(\partial \Omega )${{L}^{p}}(\partial \Omega )$. Moreover, the uniform estimates are found.

{{H}^{p}}${{H}^{p}}$ estimate for the multilinear operators which are finite sums of pointwise products of singular integrals and fractional integrals is given. An application to Sobolev space and some examples are also given.