Drawing on the analogy between any unary first-order quantifier and a “face operator,” this paper establishes several connections between model theory and homotopy theory. The concept of simplicial set is brought into play to describe the formulae of any first-order language L, the definable subsets of any L-structure, as well as the type spaces of any theory expressed in L. An adjunction result is then proved between the category of o-minimal structures and a subcategory of the category of linearly ordered simplicial sets with distinguished vertices.

Let $k=\mathbb{C}$ be the field of complex numbers. In this article we construct Hodge realization functors defined on the triangulated categories of étale motives with rational coefficients. Our construction extends to every smooth quasi-projective $k$-scheme, the construction done by Nori over a field, and relies on the original version of the basic lemma proved by Beĭlinson. As in the case considered by Nori, the realization functor factors through the bounded derived category of a perverse version of the Abelian category of Nori motives.

We provide a brief description of the mathematics that led to Daniel Quillen's introduction of model categories, a summary of his seminal work “Homotopical algebra”, and a brief description of some of the developments in the field since.

In this short paper we try to describe the fundamental contribution of Quillen in the development of abstract homotopy theory and we explain how he uses this theory to lay the foundations of rational homotopy theory.

This work establishes a comparison between functions on derived loop spaces (Toën and Vezzosi, Chern character, loop spaces and derived algebraic geometry, in Algebraic topology: the Abel symposium 2007, Abel Symposia, vol. 4, eds N. Baas, E. M. Friedlander, B. Jahren and P. A. Østvær (Springer, 2009), ISBN:978-3-642-01199-3) and de Rham theory. If A is a smooth commutative k-algebra and k has characteristic 0, we show that two objects, S1⊗A and ϵ(A), determine one another, functorially in A. The object S1⊗A is the S1-equivariant simplicial k-algebra obtained by tensoring A by the simplicial group S1 :=Bℤ, while the object ϵ(A) is the de Rham algebra of A, endowed with the de Rham differential, and viewed as a ϵ-dg-algebra (see the main text). We define an equivalence φ between the homotopy theory of simplicial commutative S1-equivariant k-algebras and the homotopy theory of ϵ-dg-algebras, and we show the existence of a functorial equivalence ϕ(S1 ⊗A)∼ϵ(A) . We deduce from this the comparison mentioned above, identifying the S1-equivariant functions on the derived loop space LX of a smooth k-scheme X with the algebraic de Rham cohomology of X/k. As corollaries, we obtain functorial and multiplicative versions of decomposition theorems for Hochschild homology (in the spirit of Hochschild–Kostant–Rosenberg) for arbitrary semi-separated k-schemes. By construction, these decompositions are moreover compatible with the S1-action on the Hochschild complex, on one hand, and with the de Rham differential, on the other hand.

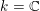
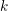
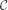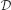Given a suitable functor T : → between model categories, we define a long exact sequence relating the homotopy groups of any X ε with those of TX, and use this to describe an obstruction theory for lifting an object G ε to . Examples include finding spaces with given homology or homotopy groups.