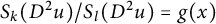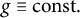1 results
Solvability of Hessian quotient equations in exterior domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 December 2023, pp. 1-31
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we study the Dirichlet problem of Hessian quotient equations of the form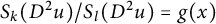
$S_k(D^2u)/S_l(D^2u)=g(x)$ in exterior domains. For 
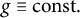$g\equiv \mbox {const.}$, we obtain the necessary and sufficient conditions on the existence of radially symmetric solutions. For g being a perturbation of a generalized symmetric function at infinity, we obtain the existence of viscosity solutions by Perron’s method. The key technique we develop is the construction of sub- and supersolutions to deal with the non-constant right-hand side g.
