Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-29T00:17:20.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Solvability of Hessian quotient equations in exterior domains

Part of: Partial differential equations Parabolic equations and systems Representations of solutions

Published online by Cambridge University Press:  14 December 2023

Limei Dai ,
Jiguang Bao Open the ORCID record for Jiguang Bao [Opens in a new window]  and
Bo Wang
Limei Dai
Affiliation:
School of Mathematics and Information Science, Weifang University, Weifang 261061, P. R. China e-mail: [email protected]
Jiguang Bao
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Beijing 100875, P. R. China e-mail: [email protected]
Bo Wang*
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing 100081, P. R. China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the Dirichlet problem of Hessian quotient equations of the form 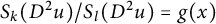$S_k(D^2u)/S_l(D^2u)=g(x)$ in exterior domains. For 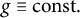$g\equiv \mbox {const.}$, we obtain the necessary and sufficient conditions on the existence of radially symmetric solutions. For g being a perturbation of a generalized symmetric function at infinity, we obtain the existence of viscosity solutions by Perron’s method. The key technique we develop is the construction of sub- and supersolutions to deal with the non-constant right-hand side g.

Keywords

Hessian quotient equationsexterior Dirichlet problemradially symmetric solutionsasymptotic behaviornecessary and sufficient conditions

MSC classification

Primary: 35K55: Nonlinear parabolic equations 35D40: Viscosity solutions 35B40: Asymptotic behavior of solutions 35B07: Axially symmetric solutions
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 31
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dai is supported by the Shandong Provincial Natural Science Foundation (Grant No. ZR2021MA054). Bao is supported by the Beijing Natural Science Foundation (Grant No. 1222017). Wang is supported by the National Natural Science Foundation of China (Grant Nos. 11971061 and 12271028), the Beijing Natural Science Foundation (Grant No. 1222017), and the Fundamental Research Funds for the Central Universities.

References

Bao, J. G. and Li, H. G., On the exterior Dirichlet problem for the Monge–Ampère equation in dimension two . Nonlinear Anal. 75(2012), 6448–6455.CrossRefGoogle Scholar
Bao, J. G., Li, H. G., and Li, Y. Y., On the exterior Dirichlet problem for Hessian equations . Trans. Amer. Math. Soc. 366(2014), 6183–6200.CrossRefGoogle Scholar
Bao, J. G., Li, H. G., and Zhang, L., Monge–Ampère equation on exterior domains . Calc. Var. 52(2015), 39–63.CrossRefGoogle Scholar
Bao, J. G., Li, H. G., and Zhang, L., Global solutions and exterior Dirichlet problem for Monge–Ampère equation in ${\mathbb{R}}^2$ . Differential Integral Equations 29(2016), 563–582.CrossRefGoogle Scholar
Bao, J. G., Xiong, J. G., and Zhou, Z. W., Existence of entire solutions of Monge–Ampère equations with prescribed asymptotic behavior . Calc. Var. 58(2019), Article no. 193, 12 pp.CrossRefGoogle Scholar
Caffarelli, L. and Li, Y. Y., An extension to a theorem of Jörgens, Calabi, and Pogorelov . Commun. Pure Appl. Math. 56(2003), 549–583.CrossRefGoogle Scholar
Caffarelli, L., Nirenberg, L., and Spruck, J., The Dirichlet problem for nonlinear second-order elliptic equations. III. Functions of the eigenvalues of the Hessian . Acta Math. 155(1985), 261–301.CrossRefGoogle Scholar
Calabi, E., Improper affine hyperspheres of convex type and a generalization of a theorem by K. Jörgens . Michigan Math. J. 5(1958), 105–126.CrossRefGoogle Scholar
Cao, X. and Bao, J. G., Hessian equations on exterior domain . J. Math. Anal. Appl. 448(2017), 22–43.CrossRefGoogle Scholar
Dai, L. M., Existence of solutions with asymptotic behavior of exterior problems of Hessian equations . Proc. Amer. Math. Soc. 139(2011), 2853–2861.CrossRefGoogle Scholar
Dai, L. M., The Dirichlet problem for Hessian quotient equations in exterior domains . J. Math. Anal. Appl. 380(2011), 87–93.CrossRefGoogle Scholar
Dai, L. M. and Bao, J. G., On uniqueness and existence of viscosity solutions to Hessian equations in exterior domains . Front. Math. China 6(2011), 221–230.CrossRefGoogle Scholar
Hong, G. H., A remark on Monge–Ampère equation over exterior domains. Preprint, 2020. https://arxiv.org/abs/2007.12479 Google Scholar
Jiang, T. Y., Li, H. G., and Li, X. L., The Dirichlet problem for Hessian quotient equations on exterior domains. Preprint, 2022, arXiv:2205.07200.Google Scholar
Jörgens, K., Über die Lösungen der Differentialgleichung $rt-{s}^2=1$ . Math. Ann. 127(1954), 130–134 (in German).CrossRefGoogle Scholar
Li, D. S. and Li, Z. S., On the exterior Dirichlet problem for Hessian quotient equations . J. Differential Equations 264(2018), 6633–6662.CrossRefGoogle Scholar
Li, H. G. and Dai, L. M., The exterior Dirichlet problem for Hessian quotient equations . J. Math. Anal. Appl. 393(2012), 534–543.CrossRefGoogle Scholar
Li, H. G., Li, X. L., and Zhao, S. Y., Hessian quotient equations on exterior domains. Preprint, 2020. https://arxiv.org/abs/2004.06908 Google Scholar
Li, Y. Y. and Lu, S. Y., Existence and nonexistence to exterior Dirichlet problem for Monge–Ampère equation . Calc. Var. 57(2018), Article no. 161, 17 pp.CrossRefGoogle Scholar
Li, Y. Y., Nguyen, L., and Wang, B., Comparison principles and Lipschitz regularity for some nonlinear degenerate elliptic equations . Calc. Var. 57(2018), Article no. 96, 29 pp.CrossRefGoogle Scholar
Pogorelov, A., On the improper convex affine hyperspheres . Geom. Dedicata 1(1972), 33–46.CrossRefGoogle Scholar
Trudinger, N. S., On the Dirichlet problem for Hessian equations . Acta Math. 175(1995), 151–164.CrossRefGoogle Scholar
Wang, C. and Bao, J. G., Necessary and sufficient conditions on existence and convexity of solutions for Dirichlet problems of Hessian equations on exterior domains . Proc. Amer. Math. Soc. 141(2013), 1289–1296.CrossRefGoogle Scholar