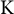We build on the recent techniques of Codogni and Patakfalvi (2021, Inventiones Mathematicae 223, 811–894), which were used to establish theorems about semi-positivity of the Chow Mumford line bundles for families of 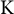$\mathrm {K}$ -semistable Fano varieties. Here, we apply the Central Limit Theorem to ascertain the asymptotic probabilistic nature of the vertices of the Harder and Narasimhan polygons. As an application of our main result, we use it to establish a filtered vector space analogue of the main technical result of Codogni and Patakfalvi (2021, Inventiones Mathematicae 223, 811–894). In doing so, we expand upon the slope stability theory, for filtered vector spaces, that was initiated by Faltings and Wüstholz (1994, Inventiones Mathematicae 116, 109–138). One source of inspiration for our abstract study of Harder and Narasimhan data, which is a concept that we define here, is the lattice reduction methods of Grayson (1984, Commentarii Mathematici Helvetic 59, 600–634). Another is the work of Faltings and Wüstholz (1994, Inventiones Mathematicae 116, 109–138), and Evertse and Ferretti (2013, Annals of Mathematics 177, 513–590), which is within the context of Diophantine approximation for projective varieties.