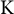1 Introduction
Our purpose here is to continue our work which is at the intersection of
![]() $\mathrm {K}$
-stability and Diophantine approximation for projective varieties [Reference Grieve11–Reference Grieve17]. In more specific terms, we expand upon the theory Harder and Narasimhan filtrations for holomorphic vector bundles on compact Riemann surfaces. Especially, we define and study asymptotic probabilistic features of Harder and Narasimhan data. (See Section 4 and Theorems 1.4 and 1.5.)
$\mathrm {K}$
-stability and Diophantine approximation for projective varieties [Reference Grieve11–Reference Grieve17]. In more specific terms, we expand upon the theory Harder and Narasimhan filtrations for holomorphic vector bundles on compact Riemann surfaces. Especially, we define and study asymptotic probabilistic features of Harder and Narasimhan data. (See Section 4 and Theorems 1.4 and 1.5.)
Recall, that Harder and Narasimhan’s theory is now classical. It was conceived in [Reference Harder and Narasimhan18]. Recently, a significant application of this theory, building on earlier work of Viehweg, has been given by Codogni and Patakfalvi [Reference Codogni and Patakfalvi4]. Among other results, in [Reference Codogni and Patakfalvi4], the theory of Harder and Narasimhan filtrations is applied to obtain results for the Chow–Mumford line bundles that arise within the context of families of
![]() $\mathrm {K}$
-stable klt Fano varieties.
$\mathrm {K}$
-stable klt Fano varieties.
For example, the concept of Harder and Narasimhan filtration is a key, more technical, tool, which is used in [Reference Codogni and Patakfalvi4], to establish the following result.
Theorem 1.1 [Reference Codogni and Patakfalvi4, Theorem 1.1(a)]
Fixing an integer
![]() $n>0$
and a rational number
$n>0$
and a rational number
![]() $v>0$
, let
$v>0$
, let
![]() $\mathcal {M}^{\mathrm {K}-\mathrm {ss}}_{n,v}$
be the moduli stack of those
$\mathcal {M}^{\mathrm {K}-\mathrm {ss}}_{n,v}$
be the moduli stack of those
![]() $\mathrm {K}$
-semistable dimension n Fano varieties, which have anti-canonical volume equal to v. Over
$\mathrm {K}$
-semistable dimension n Fano varieties, which have anti-canonical volume equal to v. Over
![]() $\mathcal {M}^{\mathrm {K}-\mathrm {ss}}_{n,v}$
, let
$\mathcal {M}^{\mathrm {K}-\mathrm {ss}}_{n,v}$
, let
![]() $\lambda $
be the Chow–Mumford line bundle. Then
$\lambda $
be the Chow–Mumford line bundle. Then
![]() $\lambda $
and its descent along the good moduli space morphism
$\lambda $
and its descent along the good moduli space morphism
are numerically effective.
In terms of Harder and Narasimhan filtrations and Diophantine approximation, the main result is the theorem of Faltings and Wüstholz, from [Reference Faltings and Wüstholz8], and the refinement which was established by Evertse and Ferretti in [Reference Evertse and Ferretti6]. Here, in Theorem 1.2, we state a version of that result. McKinnon and Roth [Reference McKinnon and Roth20] formulated a corresponding statement for linear systems.
Investigations and expansions of Schmidt’s Subspace Theorem, from the viewpoint of linear systems, is another topic of continued recent and ongoing interest [Reference Grieve12, Reference Grieve16, Reference Heier and Levin19, Reference Ru and Vojta22, Reference Ru and Wang23]. Finally, recall, as explained in [Reference Evertse and Ferretti6], that Schmidt’s Subspace Theorem can be deduced from the inequalities of Faltings and Wüstholz. Conversely, Schmidt’s Subspace Theorem can be used to imply the inequalities of Faltings and Wüstholz. In particular, the following form of the celebrated theorem of Faltings and Wüstholz is stated in [Reference Evertse and Ferretti6, p. 514].
Theorem 1.2 [Reference Evertse and Ferretti6, Reference Faltings and Wüstholz8, Reference McKinnon and Roth20]
Let
![]() $\mathbf {K}$
be a number field,
$\mathbf {K}$
be a number field,
![]() $M_{\mathbf {K}}$
its set of places, and
$M_{\mathbf {K}}$
its set of places, and
![]() $S \subseteq M_{\mathbf {K}}$
a finite subset. For each
$S \subseteq M_{\mathbf {K}}$
a finite subset. For each
![]() $v \in M_{\mathbf {K}}$
, fix normalized absolute values
$v \in M_{\mathbf {K}}$
, fix normalized absolute values
![]() $|\cdot |_v$
so that the product theorem holds true with multiplicities equal to one. For each
$|\cdot |_v$
so that the product theorem holds true with multiplicities equal to one. For each
![]() $v \in S$
, fix linearly independent linear forms
$v \in S$
, fix linearly independent linear forms
together with nonnegative weights
![]() $d_{iv} \in \mathbb {R}_{\geqslant 0}$
which have the property that
$d_{iv} \in \mathbb {R}_{\geqslant 0}$
which have the property that
 $$ \begin{align*}\sum_{v \in S} \sum_{i=0}^n d_{iv}> n + 1 \text{.} \end{align*} $$
$$ \begin{align*}\sum_{v \in S} \sum_{i=0}^n d_{iv}> n + 1 \text{.} \end{align*} $$
Let
![]() $H_{{\mathcal O}_{\mathbb {P}^n_{\mathbf {K}}}(1)}(\cdot )$
be the multiplicative height function on projective n-space
$H_{{\mathcal O}_{\mathbb {P}^n_{\mathbf {K}}}(1)}(\cdot )$
be the multiplicative height function on projective n-space
![]() $\mathbb {P}^n_{\mathbf {K}}$
with respect to the tautological line bundle
$\mathbb {P}^n_{\mathbf {K}}$
with respect to the tautological line bundle
![]() ${\mathcal O}_{\mathbb {P}^n_{\mathbf {K}}}(1)$
. Let
${\mathcal O}_{\mathbb {P}^n_{\mathbf {K}}}(1)$
. Let
![]() $\epsilon> 0$
. Then, with this notation and hypothesis, there exists a single, effectively computable proper linear subspace
$\epsilon> 0$
. Then, with this notation and hypothesis, there exists a single, effectively computable proper linear subspace
such that the system
 $$ \begin{align*}\frac{| \ell_{iv}(x) |_v }{ \max_{0 \leqslant i \leqslant n } |x_i|_v} \leqslant H_{{\mathcal O}_{\mathbb{P}^n}(1)}(x)^{-d_{iv}} \text{,} \end{align*} $$
$$ \begin{align*}\frac{| \ell_{iv}(x) |_v }{ \max_{0 \leqslant i \leqslant n } |x_i|_v} \leqslant H_{{\mathcal O}_{\mathbb{P}^n}(1)}(x)^{-d_{iv}} \text{,} \end{align*} $$
for
![]() $v \in S$
and
$v \in S$
and
![]() $i = 0,\dots ,n$
, admits at most a finite number of solutions
$i = 0,\dots ,n$
, admits at most a finite number of solutions
Finally, we mention our recent result, from [Reference Grieve14], which is at the intersection of
![]() $\mathrm {K}$
-stability and Diophantine approximation. It establishes, in particular, that the concept of
$\mathrm {K}$
-stability and Diophantine approximation. It establishes, in particular, that the concept of
![]() $\mathrm {K}$
-instability for Fano varieties has implications for instances of Vojta’s Main Conjecture.
$\mathrm {K}$
-instability for Fano varieties has implications for instances of Vojta’s Main Conjecture.
Theorem 1.3 [Reference Grieve14, Theorem 1.1]
Let
![]() $\mathbf {K}$
be a number field, and fix a finite set of places S of
$\mathbf {K}$
be a number field, and fix a finite set of places S of
![]() $\mathbf {K}$
. Suppose that X is a
$\mathbf {K}$
. Suppose that X is a
![]() $\mathbb {Q}$
-Fano variety with canonical singularities, defined over
$\mathbb {Q}$
-Fano variety with canonical singularities, defined over
![]() $\mathbf {K}$
, and which is not
$\mathbf {K}$
, and which is not
![]() $\mathrm {K}$
-stable. Then, over X, there exists a nonzero, irreducible, and reduced effective Cartier divisor E, which is defined over some finite extension field
$\mathrm {K}$
-stable. Then, over X, there exists a nonzero, irreducible, and reduced effective Cartier divisor E, which is defined over some finite extension field
![]() $\mathbf {F} / \mathbf {K}$
, with
$\mathbf {F} / \mathbf {K}$
, with
![]() $\mathbf {K} \subseteq \mathbf {F} \subseteq \overline {\mathbf {K}}$
, for which the inequalities predicted by Vojta’s Main Conjecture hold true in the following sense. Let
$\mathbf {K} \subseteq \mathbf {F} \subseteq \overline {\mathbf {K}}$
, for which the inequalities predicted by Vojta’s Main Conjecture hold true in the following sense. Let
![]() $\mathbb {E}$
be the birational divisor that is determined by E. Let
$\mathbb {E}$
be the birational divisor that is determined by E. Let
be a birational divisor over X that has the two properties that:
-
(i) the traces of each of the
 $\mathbb {D}_i$
are linearly equivalent to the trace of
$\mathbb {D}_i$
are linearly equivalent to the trace of
 $\mathbb {E}$
on some fixed normal proper model
$\mathbb {E}$
on some fixed normal proper model
 $X'$
of X, defined over
$X'$
of X, defined over
 $\mathbf {F}$
; and
$\mathbf {F}$
; and -
(ii) the traces of each of these divisors
 $\mathbb {D}_i$
, for
$\mathbb {D}_i$
, for
 $i = 1,\dots ,q$
, intersect properly on this model
$i = 1,\dots ,q$
, intersect properly on this model
 $X'$
.
$X'$
.
Let B be a big line bundle on X, and let
![]() $\epsilon> 0$
. Then the inequality
$\epsilon> 0$
. Then the inequality
is valid for all
![]() $\mathbf {K}$
-rational points
$\mathbf {K}$
-rational points
![]() $x \in X(\mathbf {K}) \setminus Z(\mathbf {K})$
and
$x \in X(\mathbf {K}) \setminus Z(\mathbf {K})$
and
![]() $Z \subsetneq X$
some proper Zariski closed subset defined over
$Z \subsetneq X$
some proper Zariski closed subset defined over
![]() $\mathbf {K}$
.
$\mathbf {K}$
.
In (1.1),
![]() $\lambda _{\mathbb {D},v}(\cdot )$
is the birational Weil function of
$\lambda _{\mathbb {D},v}(\cdot )$
is the birational Weil function of
![]() $\mathbb {D}$
with respect to the place
$\mathbb {D}$
with respect to the place
![]() $v \in S$
. (We refer to [Reference Ru and Vojta22, Section 4] and [Reference Grieve14, Section 3] for more details.)
$v \in S$
. (We refer to [Reference Ru and Vojta22, Section 4] and [Reference Grieve14, Section 3] for more details.)
Here, our main result builds on the techniques from [Reference Codogni and Patakfalvi4] and establishes, in particular, a Central Limit Theorem for the vertices of the Harder–Narasimhan polygons. (See Theorem 1.4 and Sections 4 and 6 for precise details.)
To place matters into perspective, note that an essential feature to the work of Faltings and Wüstholz [Reference Faltings and Wüstholz8] is their theory of slope semi-stability for filtered vector spaces. Over the years, this theory has been developed and has produced significant applications. (See, for example, [Reference Chen3, Reference Faltings7, Reference Fujimori9, Reference Totaro24] and the references therein.)
Our main results here (Theorems 1.4 and 1.5) are natural extensions to this circle of ideas. Aside from being of an intrinsic interest in their own right, they provide continued evidence for the existence of fruitful, and yet to be discovered, interactions among the areas of K-stability, positivity questions for polarized projective varieties and Diophantine arithmetic geometry.
Let us now formulate Theorem 1.4. In Section 6 (see Theorem 6.1), we state a slight variant, which is phrased in terms of our concept of Harder and Narasimhan data. In our formulation of Theorem 1.4, we define this concept in passing.
Theorem 1.4 Fix a rank vector
![]() $\overrightarrow {r} := (r_1,\dots ,r_\ell )\text {,}$
that consists of positive integers
$\overrightarrow {r} := (r_1,\dots ,r_\ell )\text {,}$
that consists of positive integers
![]() $r_i$
, for
$r_i$
, for
![]() $i = 1,\dots ,\ell $
, fix a collection of strictly decreasing collection of rational numbers
$i = 1,\dots ,\ell $
, fix a collection of strictly decreasing collection of rational numbers
![]() $\mu _1> \cdots > \mu _\ell $
, and let
$\mu _1> \cdots > \mu _\ell $
, and let
![]() $\overrightarrow {d} := (d_1,\dots ,d_\ell )$
be the resulting degree vector, which is determined by the condition that
$\overrightarrow {d} := (d_1,\dots ,d_\ell )$
be the resulting degree vector, which is determined by the condition that
![]() $d_i := \mu _i r_i \text {,}$
for
$d_i := \mu _i r_i \text {,}$
for
![]() $i = 1,\dots ,\ell $
. Assume that such Harder and Narasimhan data are positive in the sense that
$i = 1,\dots ,\ell $
. Assume that such Harder and Narasimhan data are positive in the sense that
 $$ \begin{align*}\left|\overrightarrow{d}\right| := \sum_{i=1}^\ell d_i> 0 \text{.}\end{align*} $$
$$ \begin{align*}\left|\overrightarrow{d}\right| := \sum_{i=1}^\ell d_i> 0 \text{.}\end{align*} $$
Let
![]() $p_i := r_i / r\text {,}$
for
$p_i := r_i / r\text {,}$
for
![]() $i = 1,\dots ,\ell $
, and let
$i = 1,\dots ,\ell $
, and let
![]() $\mathcal {Y} := \mathcal {Y}\left ([\ell ],p_1,\dots ,p_{\ell }\right )$
be the discrete probability space on the set
$\mathcal {Y} := \mathcal {Y}\left ([\ell ],p_1,\dots ,p_{\ell }\right )$
be the discrete probability space on the set
![]() $[\ell ] := \{1,\dots ,\ell \}$
and having probability measures
$[\ell ] := \{1,\dots ,\ell \}$
and having probability measures
![]() $p_1,\dots ,p_\ell $
. Let
$p_1,\dots ,p_\ell $
. Let
![]() $Y_j := Y_j(\overrightarrow {\mu })$
be a sequence of independent and identically distributed random variables of
$Y_j := Y_j(\overrightarrow {\mu })$
be a sequence of independent and identically distributed random variables of
![]() $\mathcal {Y}$
that take value
$\mathcal {Y}$
that take value
![]() $\mu _i := d_i / r_i$
on i. Then, within this context, given a nonnegative integer
$\mu _i := d_i / r_i$
on i. Then, within this context, given a nonnegative integer
![]() $z \geqslant 0$
, it holds true that
$z \geqslant 0$
, it holds true that
 $$ \begin{align*}\lim_{m \to \infty} \operatorname{Prob}\left( \sum_{j=1}^m Y_j \geqslant z \right) = 1 \text{.}\end{align*} $$
$$ \begin{align*}\lim_{m \to \infty} \operatorname{Prob}\left( \sum_{j=1}^m Y_j \geqslant z \right) = 1 \text{.}\end{align*} $$
We prove Theorem 1.4 in Section 6. As one application, it implies a filtered vector space analogue of [Reference Codogni and Patakfalvi4, Theorem 5.11]. This is the content of Theorem 1.5, whose formulation is more technical.
To get a flavor, consider a filtered vector space
Then, by the theory of Faltings and Wüstholz [Reference Faltings and Wüstholz8, Section 4], it admits a canonical Harder and Narasimhan filtration
The Harder and Narasimhan data
![]() $\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
are obtained from the Harder and Narasimhan filtration (1.3). It consists of the slope and rank vectors. We refer to Example 4.2 for further details.
$\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
are obtained from the Harder and Narasimhan filtration (1.3). It consists of the slope and rank vectors. We refer to Example 4.2 for further details.
To get a sense for what we mean by positive Harder and Narasimhan data, respectively, denote the slope, rank, and degree vectors as
Here,
for
![]() $i = 1,\dots , \ell $
. The Harder and Narasimhan data
$i = 1,\dots , \ell $
. The Harder and Narasimhan data
![]() $\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
are called positive if
$\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
are called positive if
 $$ \begin{align*}\left|\overrightarrow{d}\right| := \sum_{i=1}^{\ell} d_i> 0 \text{.} \end{align*} $$
$$ \begin{align*}\left|\overrightarrow{d}\right| := \sum_{i=1}^{\ell} d_i> 0 \text{.} \end{align*} $$
The intuition for Theorem 1.5 is that, fixing
![]() $m \geqslant 0$
, we want to study, inside of
$m \geqslant 0$
, we want to study, inside of
![]() $V^{\otimes m}$
, the collection of those subspaces that are spanned by m-fold tensor products of the Harder and Narasimhan subspaces
$V^{\otimes m}$
, the collection of those subspaces that are spanned by m-fold tensor products of the Harder and Narasimhan subspaces
![]() $V_i$
, which appear in the Harder and Narasimhan filtration (1.3).
$V_i$
, which appear in the Harder and Narasimhan filtration (1.3).
In more detail, for each
set
 $$ \begin{align*}v_{\overrightarrow{\mu}}(\mathbf{a}) := \sum_{j=1}^m \mu_{a_j} \text{,} \end{align*} $$
$$ \begin{align*}v_{\overrightarrow{\mu}}(\mathbf{a}) := \sum_{j=1}^m \mu_{a_j} \text{,} \end{align*} $$
and fixing a nonnegative integer
![]() $z \geqslant 0$
, set
$z \geqslant 0$
, set
 $$ \begin{align*}S_{m,z} (\overrightarrow{\mu}):= \left\{ \mathbf{a} = (a_1,\dots,a_m) \in [\ell]^m : \sum_{j=1}^m \mu_{a_j} \geqslant z \right\} \text{.} \end{align*} $$
$$ \begin{align*}S_{m,z} (\overrightarrow{\mu}):= \left\{ \mathbf{a} = (a_1,\dots,a_m) \in [\ell]^m : \sum_{j=1}^m \mu_{a_j} \geqslant z \right\} \text{.} \end{align*} $$
Finally, writing the elements of
![]() $[\ell ]^m$
in decreasing order with respect to
$[\ell ]^m$
in decreasing order with respect to
![]() $v_{\overrightarrow {\mu }}(\cdot )$
, denoted as
$v_{\overrightarrow {\mu }}(\cdot )$
, denoted as
put
 $$ \begin{align} H^{\# S_{m,z}(\overrightarrow{\mu})} := \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \bigotimes_{j=1}^m V_{a_{ji}} \text{.} \end{align} $$
$$ \begin{align} H^{\# S_{m,z}(\overrightarrow{\mu})} := \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \bigotimes_{j=1}^m V_{a_{ji}} \text{.} \end{align} $$
Having fixed some notation and context, our filtered vector space analogue of [Reference Codogni and Patakfalvi4, Theorem 5.11] is formulated in the following way. It is an application of Theorem 1.4 and is proved in Section 7.
Theorem 1.5 Suppose that a filtered vector space V has positive Harder and Narasimhan data
![]() $\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
. Fixing a nonnegative integer
$\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
. Fixing a nonnegative integer
![]() $z \geqslant 0$
, for each nonnegative integer
$z \geqslant 0$
, for each nonnegative integer
![]() $m \geqslant 0$
, let
$m \geqslant 0$
, let
![]() $H^{\# S_{m,z}(\overrightarrow {\mu })}$
be the subspace of
$H^{\# S_{m,z}(\overrightarrow {\mu })}$
be the subspace of
![]() $V^{\otimes m}$
that is given by (1.4). Then, with this notation and hypothesis, it holds true that
$V^{\otimes m}$
that is given by (1.4). Then, with this notation and hypothesis, it holds true that
 $$ \begin{align*}\lim_{m \to \infty} \frac{\dim H^{\# S_{m,z} (\overrightarrow{\mu})} }{ \dim V^{\otimes m} } = 1 \text{.} \end{align*} $$
$$ \begin{align*}\lim_{m \to \infty} \frac{\dim H^{\# S_{m,z} (\overrightarrow{\mu})} }{ \dim V^{\otimes m} } = 1 \text{.} \end{align*} $$
As some additional context and motivation for our abstract formulation of [Reference Codogni and Patakfalvi4, Theorem 5.11] (see Theorems 1.4 and 1.5), we mention that a concept of Harder and Narasimhan Polygons emerged as a tool for expanding upon Harder and Narasimhan’s theory of filtrations for vector bundles on curves. This was popularized by Grayson in his work on lattice reduction theory [Reference Grayson10]. We refer to [Reference Casselman2] for an exposition. Here, our point of departure is to associate a polygon with Harder and Narasimhan data. This is made precise in Section 4.
Our results also give impetus for further investigation. As some examples, the concept of Harder and Narasimhan data (see Definition 4.1) raises the question of explicit and robust construction thereof, and especially with applications in geometric and arithmetic contexts.
In the direction of Theorem 1.4, there is the question of the rate in which the limit that appears in its conclusion is actually achieved. Furthermore, it remains interesting to understand the extent to which Theorems 1.4 and 1.5, or variants thereof, will have applications for geometric and arithmetic aspects of filtered linear series. Such results would complement those of our recent work [Reference Grieve17] (among others).
In Section 2, we discuss the Laws of Large Numbers and state the Central Limit Theorem for independent and identically distributed random variables. In Section 3, we recall the classical theory of Harder and Narasimhan and state the main result from [Reference Harder and Narasimhan18]. (See Theorem 3.1.) In Section 5, we discuss a key motivational example from [Reference Codogni and Patakfalvi4]. It also provides additional context and motivation for Theorem 1.5. Again, the concept of Harder and Narasimhan data is made precise in Section 4. Respectively, Theorems 1.4 and 1.5 are established in Sections 6 and 7.
Throughout this article, unless explicitly stated otherwise, all schemes, stacks, and vector spaces are defined over a fixed algebraically closed characteristic zero base field
![]() $\mathbf {k}$
.
$\mathbf {k}$
.
2 Laws of large numbers
In this section, we state the three main Laws of Large Numbers. Our approach mostly follows [Reference Billingsley1, Reference Durrett5, Reference Murty21].
First of all, in heuristic terms, the Weak Law of Large Numbers says that if n is large, then there is only a small chance that the fraction of heads in n tosses will be far from
![]() $1/2$
. In more precise terms, it is formulated in the following way.
$1/2$
. In more precise terms, it is formulated in the following way.
Theorem 2.1 (Weak Law of Large Numbers; cf. [Reference Billingsley1, p. 86], [Reference Durrett5, Theorem 2.2.12])
Let
![]() $X_1, X_2,\dots $
be a sequence of independent and identically distributed simple random variables with identical expected values
$X_1, X_2,\dots $
be a sequence of independent and identically distributed simple random variables with identical expected values
for each n. Put
Suppose that
![]() $y> 0$
. Then
$y> 0$
. Then
Turning to the Strong Law of Large Numbers, recall that it expands upon the Weak Law (Theorem 2.1).
Theorem 2.2 (Strong Law of Large Numbers; cf. [Reference Billingsley1, Theorem 6.1], [Reference Durrett5, Theorem 2.4.1])
Let
![]() $X_1, X_2,\dots $
be a sequence of independent and identically distributed simple random variables with identical expected values
$X_1, X_2,\dots $
be a sequence of independent and identically distributed simple random variables with identical expected values
for each n. Put
It then holds true that
Finally, we state the Central Limit Theorem. It also extends the Weak Law of Large Numbers. An attractive self-contained proof via the theory of Fourier transforms is given in [Reference Murty21, Section 3.15].
Theorem 2.3 (Central Limit Theorem; cf. [Reference Billingsley1, Theorem 27.1], [Reference Durrett5, Theorem 3.4.1], [Reference Murty21, Theorem 3.16])
Let
![]() $\Phi $
be a standard normal random variable and so, in particular, having probability density function
$\Phi $
be a standard normal random variable and so, in particular, having probability density function
Let
![]() $X_1, X_2,\dots $
be a sequence of independent random variables having the same distribution with mean
$X_1, X_2,\dots $
be a sequence of independent random variables having the same distribution with mean
![]() $\mu $
and positive finite variance
$\mu $
and positive finite variance
![]() $\sigma ^2$
. Let
$\sigma ^2$
. Let
It then holds true that
Furthermore,
3 The theory of Harder and Narasimhan
Here, we recall, from [Reference Harder and Narasimhan18], the theory of Harder and Narasimhan. In what follows, C denotes a nonsingular projective algebraic curve over an arbitrary characteristic algebraically closed base field. By abuse of terminology, we fail to distinguish among the concept of finite rank locally free
![]() ${\mathcal O}_C$
-modules and total spaces of vector bundles. On the other hand, if
${\mathcal O}_C$
-modules and total spaces of vector bundles. On the other hand, if
![]() $\mathcal {E}$
is a vector bundle on C and
$\mathcal {E}$
is a vector bundle on C and
![]() $\mathcal {F}$
a locally free submodule, then
$\mathcal {F}$
a locally free submodule, then
![]() $\mathcal {F}$
is called a subvector bundle if the quotient
$\mathcal {F}$
is called a subvector bundle if the quotient
![]() $\mathcal {E} / \mathcal {F}$
is locally free.
$\mathcal {E} / \mathcal {F}$
is locally free.
If
![]() $\mathcal {E}$
is a nonzero vector bundle on C, then its slope is
$\mathcal {E}$
is a nonzero vector bundle on C, then its slope is
Here,
is the rank of
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
is the determinant line bundle.
If a nonzero vector bundle
![]() $\mathcal {E}$
on C has the property that
$\mathcal {E}$
on C has the property that
for all nonzero proper subbundles
![]() $\mathcal {F}$
, then it is called semistable. By [Reference Harder and Narasimhan18, Lemma 1.3.7], if a nonzero vector bundle
$\mathcal {F}$
, then it is called semistable. By [Reference Harder and Narasimhan18, Lemma 1.3.7], if a nonzero vector bundle
![]() $\mathcal {E}$
is not semistable, then it admits a unique nonzero subbundle
$\mathcal {E}$
is not semistable, then it admits a unique nonzero subbundle
![]() $\mathcal {F}$
which strongly contradicts semistability in the following sense:
$\mathcal {F}$
which strongly contradicts semistability in the following sense:
-
(i)
 $\mathcal {F}$
is semi-stable; and
$\mathcal {F}$
is semi-stable; and -
(ii) if
 $\mathcal {G}$
is a subbundle of
$\mathcal {G}$
is a subbundle of
 $\mathcal {E}$
which contains
$\mathcal {E}$
which contains
 $\mathcal {F}$
as a subbundle, then
$\mathcal {F}$
as a subbundle, then  $$ \begin{align*}\mu(\mathcal{F})> \mu(\mathcal{G})\text{.}\end{align*} $$
$$ \begin{align*}\mu(\mathcal{F})> \mu(\mathcal{G})\text{.}\end{align*} $$
The concept of subbundles which strongly contradict semistability is a key technical point in establishing the existence and uniqueness of the Harder and Narasimhan (canonical) filtrations. This fundamental result of [Reference Harder and Narasimhan18] is formulated in the following way.
Theorem 3.1 [Reference Harder and Narasimhan18, Section 1.3]
Let C denote a nonsingular projective algebraic curve over an arbitrary characteristic algebraically closed base field. Let
![]() $\mathcal {E}$
be a nonzero vector bundle on C. Then
$\mathcal {E}$
be a nonzero vector bundle on C. Then
![]() $\mathcal {E}$
admits a uniquely determined flag of subvector bundles
$\mathcal {E}$
admits a uniquely determined flag of subvector bundles
which has the two properties that:
-
(i) the successive quotients
 $\mathcal {E}_i / \mathcal {E}_{i-1}$
are semistable for
$\mathcal {E}_i / \mathcal {E}_{i-1}$
are semistable for
 $i = 1,\dots ,\ell $
; and
$i = 1,\dots ,\ell $
; and -
(ii) the slopes of the successive quotients are strictly decreasing in the sense that
for $$ \begin{align*}\mu(\mathcal{E}_i / \mathcal{E}_{i-1})> \mu(\mathcal{E}_{i+1} / \mathcal{E}_i), \end{align*} $$
$$ \begin{align*}\mu(\mathcal{E}_i / \mathcal{E}_{i-1})> \mu(\mathcal{E}_{i+1} / \mathcal{E}_i), \end{align*} $$
 $i = 1,\dots ,\ell -1$
.
$i = 1,\dots ,\ell -1$
.
In working with the Harder and Narasimhan filtrations (3.1), in what follows, we find it useful to put
for
![]() $i = 1,\dots ,\ell $
. By this notation
$i = 1,\dots ,\ell $
. By this notation
![]() $r_i> 0\text {,}$
for all
$r_i> 0\text {,}$
for all
![]() $i = 1,\dots ,\ell $
,
$i = 1,\dots ,\ell $
,
and
 $$ \begin{align*}\sum_{i=1}^\ell r_i = r \text{.} \end{align*} $$
$$ \begin{align*}\sum_{i=1}^\ell r_i = r \text{.} \end{align*} $$
Moreover, if
then
 $$ \begin{align*}\mu = \frac{ \sum_{i=1}^\ell \mu_i r_i }{r} \text{.} \end{align*} $$
$$ \begin{align*}\mu = \frac{ \sum_{i=1}^\ell \mu_i r_i }{r} \text{.} \end{align*} $$
Finally, we refer to the bundles
![]() $\mathcal {E}_i$
, for
$\mathcal {E}_i$
, for
![]() $i = 1,\dots ,\ell $
, which arise in the filtration (3.1), as the Harder and Narasimhan subbundles of
$i = 1,\dots ,\ell $
, which arise in the filtration (3.1), as the Harder and Narasimhan subbundles of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
4 The Harder and Narasimhan polygons and their vertices
A concept of Harder and Narasimhan Polygons emerged as a tool for expanding upon Harder and Narasimhan’s theory of filtrations for vector bundles on curves. This was popularized by Grayson in his work on lattice reduction theory [Reference Grayson10]. We refer to the article [Reference Casselman2], by Casselman, for an exposition. Here, our viewpoint is to associate a polygon with Harder and Narasimhan data. We make this precise in Definition 4.1.
Another context in which a fruitful theory of Narasimhan Polygons has emerged is that of filtered vector spaces. Such developments have been made possible by work of Faltings and Wüstholz [Reference Faltings and Wüstholz8], Chen [Reference Chen3], and others. In Example 4.2, and because of its relevance to Theorem 1.5, we indicate how our notion of Harder and Narasimhan data fits within the framework of the Harder and Narasimhan filtration that is associated with each filtered vector space.
Within the context of Diophantine approximation, the theory of Harder and Narasimhan filtrations for vector spaces is an important aspect of the work of Faltings and Wüstholz [Reference Faltings and Wüstholz8]. Similar filtrations together with a theory of polygons arise, more recently, in the work of Evertse and Ferretti (see [Reference Evertse and Ferretti6, Section 15]).
Of interest, for our purposes here, is the asymptotic probabilistic nature of such Harder and Narasimhan Polygons. Exactly what is meant by this is made precise below.
Definition 4.1 By Harder and Narasimhan data, is meant a collection of strictly decreasing rational numbers
together with a collection of positive integers
![]() $r_i> 0$
, for
$r_i> 0$
, for
![]() $i = 1,\dots ,\ell $
. Denote such data by
$i = 1,\dots ,\ell $
. Denote such data by
![]() $\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
. Here,
$\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
. Here,
The integer
![]() $\ell $
is called the length.
$\ell $
is called the length.
Put
 $$ \begin{align*}r := \sum_{i=1}^\ell r_i\text{.}\end{align*} $$
$$ \begin{align*}r := \sum_{i=1}^\ell r_i\text{.}\end{align*} $$
This is the rank, and the
![]() $r_i$
are the subquotient ranks.
$r_i$
are the subquotient ranks.
Finally, upon setting
for
![]() $i = 1,\dots ,\ell $
, and
$i = 1,\dots ,\ell $
, and
we obtain the degree vector. If
 $$ \begin{align*}\left| \overrightarrow{d} \right| := \sum_{i=1}^\ell d_i> 0 \text{,}\end{align*} $$
$$ \begin{align*}\left| \overrightarrow{d} \right| := \sum_{i=1}^\ell d_i> 0 \text{,}\end{align*} $$
then the Harder and Narasimhan data
![]() $\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
are said to have positive degree.
$\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
are said to have positive degree.
Furthermore, set
where
for
![]() $i = 1,\dots ,\ell $
. Then the
$i = 1,\dots ,\ell $
. Then the
![]() $p_i$
are the Harder and Narasimhan probabilities, whereas
$p_i$
are the Harder and Narasimhan probabilities, whereas
![]() $\overrightarrow {p}$
is the Harder and Narasimhan probability vector.
$\overrightarrow {p}$
is the Harder and Narasimhan probability vector.
Finally, similar to the approach of [Reference Grayson10, Definition 1.10 and Discussion 1.16] and [Reference Casselman2, p. 630], the vertices of Harder and Narasimhan data
![]() $\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r} \right )$
are defined to be the collection of points
$\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r} \right )$
are defined to be the collection of points
(Compare also with [Reference Chen3, Remark 2.2.8].)
Example 4.2 As in [Reference Faltings and Wüstholz8, Section 4], Let V be a finite-dimensional
![]() $\mathbf {k}$
-vector space, and consider, given a collection of real numbers
$\mathbf {k}$
-vector space, and consider, given a collection of real numbers
a filtration of the form
The filtered vector space (4.1) is called semistable if it holds true that
for each proper nonzero subspace
In (4.2), the slope of
![]() $V'$
is calculated with respect to the induced filtration.
$V'$
is calculated with respect to the induced filtration.
As noted by Faltings and Wüstholz, each such filtered vector space (4.1) admits a canonical Harder and Narasimhan filtration. In more specific terms, there exists a flag of vector spaces
which have the property that each successive quotient
![]() $V_i / V_{i - 1}$
, for
$V_i / V_{i - 1}$
, for
![]() $i = 1,\dots ,\ell $
, is semistable (which respect to the induced filtration), and furthermore, the slopes
$i = 1,\dots ,\ell $
, is semistable (which respect to the induced filtration), and furthermore, the slopes
![]() $\mu (V_i / V_{i-1})$
of the successive quotients are strictly decreasing.
$\mu (V_i / V_{i-1})$
of the successive quotients are strictly decreasing.
Within this context, putting
for
![]() $i = 1,\dots ,\ell $
, and setting
$i = 1,\dots ,\ell $
, and setting
yields Harder and Narasimhan data
![]() $\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
.
$\operatorname {HN}(\overrightarrow {\mu },\overrightarrow {r})$
.
5 Tensor products of Harder and Narasimhan subbundles
To provide motivation for our construction with vertices of Harder and Narasimhan subbundles in Section 6, here we discuss a related construction of [Reference Codogni and Patakfalvi4], which was the starting point for our investigation here.
These constructions from [Reference Codogni and Patakfalvi4] build on Viehweg’s fiber product approach from [Reference Viehweg25], for proving weak positivity results for direct images of tensor powers of relative canonical sheaves.
A representative example for the techniques of [Reference Codogni and Patakfalvi4, Section 5] is explained in [Reference Codogni and Patakfalvi4, Remark 5.6]. We reproduce some of that discussion here. It provides motivation for our analogous results which apply to the context of filtered vector spaces. (See Theorem 1.5 and Example 4.2.)
In particular, working over the projective line
![]() $\mathbb {P}^1_{\mathbf {k}}$
, consider the case of a vector bundle
$\mathbb {P}^1_{\mathbf {k}}$
, consider the case of a vector bundle
where
![]() $b_i \in \mathbb {Z}$
and
$b_i \in \mathbb {Z}$
and
![]() $b_i < b_{i+1}\text {,}$
for
$b_i < b_{i+1}\text {,}$
for
![]() $i = 1,\dots ,\ell -1$
.
$i = 1,\dots ,\ell -1$
.
With respect to the Harder and Narasimhan filtrations for
![]() $\mathcal {E}$
, the ith Harder and Narasimhan submodule is
$\mathcal {E}$
, the ith Harder and Narasimhan submodule is
The ith subquotient slope is thus
Now, fixing a positive integer
![]() $m> 0$
, the idea is to study via probabilistic methods, inside of
$m> 0$
, the idea is to study via probabilistic methods, inside of
![]() $\mathcal {E}^{\otimes m}$
, the prevalence of those submodules which are obtained via the m-fold tensor products
$\mathcal {E}^{\otimes m}$
, the prevalence of those submodules which are obtained via the m-fold tensor products
Here,
![]() $a_i \in \{1,\dots ,\ell \}\text {,}$
for
$a_i \in \{1,\dots ,\ell \}\text {,}$
for
![]() $i = 1,\dots ,m$
, and
$i = 1,\dots ,m$
, and
 $$ \begin{align*}\sum_{i=1}^m \mu_{a_i} \geqslant z \text{,} \end{align*} $$
$$ \begin{align*}\sum_{i=1}^m \mu_{a_i} \geqslant z \text{,} \end{align*} $$
for
![]() $z \in \mathbb {Z}_{\geqslant 0}$
some given nonnegative integer.
$z \in \mathbb {Z}_{\geqslant 0}$
some given nonnegative integer.
In Section 6, we generalize this construction from [Reference Codogni and Patakfalvi4], so as to treat the more general context of Harder and Narasimhan vertices.
6 Statement of main theorem and its proof
In order to state our main theorem (see Theorem 6.1), let us first consider the construction from Section 5 in a slightly more general context.
Let
![]() $[\ell ]:= \{1,\dots ,\ell \}\text {.}$
Fixing a positive integer
$[\ell ]:= \{1,\dots ,\ell \}\text {.}$
Fixing a positive integer
![]() $m \in \mathbb {Z}_{>0}$
, let
$m \in \mathbb {Z}_{>0}$
, let
![]() $[\ell ]^m$
be the m-fold Cartesian product of
$[\ell ]^m$
be the m-fold Cartesian product of
![]() $[\ell ]$
.
$[\ell ]$
.
Let
![]() $\succ $
be the partial order on
$\succ $
be the partial order on
![]() $[\ell ]^m$
that is defined in the following way. If
$[\ell ]^m$
that is defined in the following way. If
![]() $\mathbf {a}, \mathbf {b} \in [\ell ]^m\text {,}$
then
$\mathbf {a}, \mathbf {b} \in [\ell ]^m\text {,}$
then
![]() $\mathbf {a} \succeq \mathbf {b}$
if
$\mathbf {a} \succeq \mathbf {b}$
if
![]() $a_j \geqslant b_j$
for all
$a_j \geqslant b_j$
for all
![]() $j = 1,\dots ,m$
, whereas
$j = 1,\dots ,m$
, whereas
![]() $\mathbf {a} \succ \mathbf {b}$
if
$\mathbf {a} \succ \mathbf {b}$
if
![]() $\mathbf {a} \succeq \mathbf {b}$
and
$\mathbf {a} \succeq \mathbf {b}$
and
![]() $a_j> b_j$
for some
$a_j> b_j$
for some
![]() $j = 1,\dots , m$
.
$j = 1,\dots , m$
.
Now, fix Harder and Narasimhan data
![]() $\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
. Of particular interest is the case that the Harder and Narasimhan data
$\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
. Of particular interest is the case that the Harder and Narasimhan data
![]() $\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
have positive degree. However, on the other hand, we do not impose that condition for the present time being.
$\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
have positive degree. However, on the other hand, we do not impose that condition for the present time being.
Inside of
![]() $[\ell ]^m$
, define the subset
$[\ell ]^m$
, define the subset
![]() $S_{m,z}(\overrightarrow {\mu })$
, for
$S_{m,z}(\overrightarrow {\mu })$
, for
![]() $z \in \mathbb {Z}_{\geqslant 0}$
a fixed nonnegative integer, by the condition that
$z \in \mathbb {Z}_{\geqslant 0}$
a fixed nonnegative integer, by the condition that
 $$ \begin{align*}S_{m,z}\left(\overrightarrow{\mu}\right) := \left\{ \mathbf{a} = (a_1,\dots,a_m) \in [\ell]^m : \sum_{j=1}^m \mu_{a_j} \geqslant z \right\} \text{.} \end{align*} $$
$$ \begin{align*}S_{m,z}\left(\overrightarrow{\mu}\right) := \left\{ \mathbf{a} = (a_1,\dots,a_m) \in [\ell]^m : \sum_{j=1}^m \mu_{a_j} \geqslant z \right\} \text{.} \end{align*} $$
If
![]() $ \mathbf {a} \in [\ell ]^m \text {,} $
then put
$ \mathbf {a} \in [\ell ]^m \text {,} $
then put
 $$ \begin{align*}v_{\overrightarrow{\mu}}(\mathbf{a}) := \sum_{j=1}^m \mu_{a_j} \text{.} \end{align*} $$
$$ \begin{align*}v_{\overrightarrow{\mu}}(\mathbf{a}) := \sum_{j=1}^m \mu_{a_j} \text{.} \end{align*} $$
The set
![]() $S_{m,z}\left (\overrightarrow {\mu }\right )$
has the following two properties:
$S_{m,z}\left (\overrightarrow {\mu }\right )$
has the following two properties:
-
(i) if
 $\mathbf {a} \in S_{m,z}(\overrightarrow {\mu })\text {,}$
$\mathbf {a} \in S_{m,z}(\overrightarrow {\mu })\text {,}$
 $\mathbf {b} \in [\ell ]^m$
, and
$\mathbf {b} \in [\ell ]^m$
, and
 $\mathbf {a} \succeq \mathbf {b}\text {,}$
then
$\mathbf {a} \succeq \mathbf {b}\text {,}$
then
 $\mathbf {b} \in S_{m,z}(\overrightarrow {\mu })\text {;}$
and
$\mathbf {b} \in S_{m,z}(\overrightarrow {\mu })\text {;}$
and -
(ii) if
 $\mathbf {a} \in [\ell ]^m\text {,}$
then
$\mathbf {a} \in [\ell ]^m\text {,}$
then
 $v_{\overrightarrow {\mu }}(\mathbf {a}) \geqslant z\text {,}$
if and only if
$v_{\overrightarrow {\mu }}(\mathbf {a}) \geqslant z\text {,}$
if and only if
 $\mathbf {a} \in S_{m,z}(\overrightarrow {\mu })\text {.}$
$\mathbf {a} \in S_{m,z}(\overrightarrow {\mu })\text {.}$
Henceforth, put
Then, upon arranging the elements of
![]() $[\ell ]^m$
in decreasing order, with respect to
$[\ell ]^m$
in decreasing order, with respect to
![]() $v_{\overrightarrow {\mu }}(\cdot )$
, we may write
$v_{\overrightarrow {\mu }}(\cdot )$
, we may write
where
and
![]() $ e = \ell m \text {.} $
In this way, we may denote elements of
$ e = \ell m \text {.} $
In this way, we may denote elements of
![]() $[\ell ]^m$
as
$[\ell ]^m$
as
for
![]() $1 \leqslant i \leqslant e$
.
$1 \leqslant i \leqslant e$
.
Recall the Harder and Narasimhan probabilities
for
![]() $i = 1,\dots ,\ell $
. Then
$i = 1,\dots ,\ell $
. Then
 $$ \begin{align*}\sum_{i=1}^\ell p_i = 1, \end{align*} $$
$$ \begin{align*}\sum_{i=1}^\ell p_i = 1, \end{align*} $$
and, for later use in Section 7, we note that
 $$ \begin{align} \sum_{i = 1}^d \prod_{j=1}^m \frac{r_{a_{ji}}}{r} = \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m \frac{r_{a_j}}{r} = \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} \text{.} \end{align} $$
$$ \begin{align} \sum_{i = 1}^d \prod_{j=1}^m \frac{r_{a_{ji}}}{r} = \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m \frac{r_{a_j}}{r} = \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} \text{.} \end{align} $$
Having fixed notation as above, our main theorem (Theorem 6.1) expands upon [Reference Codogni and Patakfalvi4, Theorem 5.11].
Theorem 6.1 Let
![]() $\operatorname {HN}\left (\overrightarrow {\mu }, \overrightarrow {r} \right )$
be Harder and Narasimhan data. Assume that
$\operatorname {HN}\left (\overrightarrow {\mu }, \overrightarrow {r} \right )$
be Harder and Narasimhan data. Assume that
![]() $\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
have positive degree. Let
$\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
have positive degree. Let
![]() $\overrightarrow {p} = (p_1,\dots ,p_\ell )$
be its probability vector. Fix a positive integer
$\overrightarrow {p} = (p_1,\dots ,p_\ell )$
be its probability vector. Fix a positive integer
![]() $m>0$
and a nonnegative integer
$m>0$
and a nonnegative integer
![]() $z \geqslant 0$
. It then holds true that
$z \geqslant 0$
. It then holds true that
 $$ \begin{align*}\lim_{m \to \infty} \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu}) } \prod_{j=1}^m p_{a_j} = 1 \text{.} \end{align*} $$
$$ \begin{align*}\lim_{m \to \infty} \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu}) } \prod_{j=1}^m p_{a_j} = 1 \text{.} \end{align*} $$
Proof Let
be the discrete probability space on the set
![]() $[\ell ]$
and having probability measures
$[\ell ]$
and having probability measures
![]() $p_1,\dots ,p_\ell $
. Let
$p_1,\dots ,p_\ell $
. Let
be a sequence of independent and identically distributed random variables of
![]() $\mathcal {Y}$
that take value
$\mathcal {Y}$
that take value
![]() $\mu _i$
on i.
$\mu _i$
on i.
Let
 $$ \begin{align*}Z_m := \sum_{j=1}^m Y_j \text{.} \end{align*} $$
$$ \begin{align*}Z_m := \sum_{j=1}^m Y_j \text{.} \end{align*} $$
Then, by considering the definition of the set
![]() $S_{m,z}(\overrightarrow {\mu })$
and the random variables
$S_{m,z}(\overrightarrow {\mu })$
and the random variables
![]() $Y_1, Y_2,\dots $
, it follows that
$Y_1, Y_2,\dots $
, it follows that
 $$ \begin{align} \operatorname{Prob}\left( Z_m \geqslant z \right) = \operatorname{Prob}\left(\sum_{j=1}^m Y_j \geqslant z \right) = \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} \text{.} \end{align} $$
$$ \begin{align} \operatorname{Prob}\left( Z_m \geqslant z \right) = \operatorname{Prob}\left(\sum_{j=1}^m Y_j \geqslant z \right) = \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} \text{.} \end{align} $$
Now, we apply the Central Limit Theorem (Theorem 2.3), to show that
To this end, first note that
![]() $\mathcal {Y}$
is a finite metric space. Moreover, the independent and identically distributed random variables
$\mathcal {Y}$
is a finite metric space. Moreover, the independent and identically distributed random variables
![]() $Y_j$
have finite mean and variance. These quantities are independent of j. Denote them, respectively, by
$Y_j$
have finite mean and variance. These quantities are independent of j. Denote them, respectively, by
![]() $\mu $
and
$\mu $
and
![]() $\sigma $
.
$\sigma $
.
The Central Limit Theorem, for independent and identically distributed random variables (Theorem 2.3), thus implies that the random variable
converges weakly to a normal distribution
![]() $\Phi $
with expected value
$\Phi $
with expected value
![]() $0$
and covariance
$0$
and covariance
![]() $\sigma ^2$
.
$\sigma ^2$
.
In particular, for each real number y, it holds true that
 $$ \begin{align*}\lim_{m\to \infty} \operatorname{Prob}\left( \frac{ Z_m - m \mu}{ \sqrt{m} } \geqslant y \right) = \operatorname{Prob}\left( \Phi \geqslant y \right) \text{.} \end{align*} $$
$$ \begin{align*}\lim_{m\to \infty} \operatorname{Prob}\left( \frac{ Z_m - m \mu}{ \sqrt{m} } \geqslant y \right) = \operatorname{Prob}\left( \Phi \geqslant y \right) \text{.} \end{align*} $$
Now, recall that the Harder and Narasimhan data
![]() $\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
have positive degree. It thus follows that
$\operatorname {HN}\left (\overrightarrow {\mu },\overrightarrow {r}\right )$
have positive degree. It thus follows that
 $$ \begin{align*}\mu = \sum_{i=1}^\ell \mu_i p_i = \frac{\sum_{i=1}^\ell \mu_i r_i }{r}> 0 \text{.} \end{align*} $$
$$ \begin{align*}\mu = \sum_{i=1}^\ell \mu_i p_i = \frac{\sum_{i=1}^\ell \mu_i r_i }{r}> 0 \text{.} \end{align*} $$
Thus, fixing a real number y, there is a positive integer
![]() $m_y> 0$
such that if
$m_y> 0$
such that if
![]() $m \geqslant m_y\text {,}$
then
$m \geqslant m_y\text {,}$
then
provided that
The above discussion implies, in particular, that
for all real numbers y. On the other hand, note that
Finally, since
and
for all m, it holds true that
This establishes the validity of the relation (6.3).
Remark 6.2 As mentioned in [Reference Codogni and Patakfalvi4, Remark 5.12], the relation (6.3) may be established using the Chebyshev’s inequality in place of the Central Limit Theorem.
7 Proof of Theorem 1.5
Finally, we indicate the manner in which Theorem 1.5 follows from Theorems 1.4 and 6.1. The key point to the proof is to adapt the proof of [Reference Codogni and Patakfalvi4, Proposition 5.9] to the context of filtered vector spaces. Having done this, Theorem 1.5 follows from Theorem 6.1, essentially because of the relation (6.1).
Proof Consider the Harder and Narasimhan filtration (1.3) that is associated with the filtered vector space (1.2). Recall, respectively, the corresponding slopes, degrees, and ranks
for
![]() $i = 1,\dots ,\ell $
. Put
$i = 1,\dots ,\ell $
. Put
For each
recall that we have put
 $$ \begin{align*}v_{\overrightarrow{\mu}}(\mathbf{a}) = \sum_{j=1}^m \mu_{a_j} \text{.} \end{align*} $$
$$ \begin{align*}v_{\overrightarrow{\mu}}(\mathbf{a}) = \sum_{j=1}^m \mu_{a_j} \text{.} \end{align*} $$
Moreover, we arrange the elements of
![]() $[\ell ]^m$
in decreasing order with respect to
$[\ell ]^m$
in decreasing order with respect to
![]() $v_{\overrightarrow{\mu}}(\cdot )$
. We write this as
$v_{\overrightarrow{\mu}}(\cdot )$
. We write this as
Finally, we have defined the set
 $$ \begin{align*}S_{m,z}(\overrightarrow{\mu}) := \left\{\mathbf{a} = (a_1,\dots,a_m) \in [\ell]^m : \sum_{j=1}^m \mu_{a_j} \geqslant z \right\} \text{,} \end{align*} $$
$$ \begin{align*}S_{m,z}(\overrightarrow{\mu}) := \left\{\mathbf{a} = (a_1,\dots,a_m) \in [\ell]^m : \sum_{j=1}^m \mu_{a_j} \geqslant z \right\} \text{,} \end{align*} $$
then
![]() $S_{m,z}(\overrightarrow {\mu })$
consists of the first
$S_{m,z}(\overrightarrow {\mu })$
consists of the first
![]() $\# S_{m,z}(\overrightarrow {\mu })$
elements of
$\# S_{m,z}(\overrightarrow {\mu })$
elements of
![]() $[\ell ]^m$
, with respect to the ordering that is induced by
$[\ell ]^m$
, with respect to the ordering that is induced by
![]() $v_{\overrightarrow {\mu}}(\cdot )$
.
$v_{\overrightarrow {\mu}}(\cdot )$
.
Now, for all
![]() $1 \leqslant i \leqslant \ell m$
, inside of
$1 \leqslant i \leqslant \ell m$
, inside of
![]() $V^{\otimes m}$
, define
$V^{\otimes m}$
, define
 $$ \begin{align*}F^i := \bigotimes_{j=1}^m V_{a_{ji}} \text{, } \end{align*} $$
$$ \begin{align*}F^i := \bigotimes_{j=1}^m V_{a_{ji}} \text{, } \end{align*} $$
 $$ \begin{align*}H^i := \sum_{j=1}^i F^i, \end{align*} $$
$$ \begin{align*}H^i := \sum_{j=1}^i F^i, \end{align*} $$
and
 $$ \begin{align*}G^i := \bigotimes_{j=1}^m \left(F^{a_{ji}} / F^{a_{ji} - 1} \right) \text{.} \end{align*} $$
$$ \begin{align*}G^i := \bigotimes_{j=1}^m \left(F^{a_{ji}} / F^{a_{ji} - 1} \right) \text{.} \end{align*} $$
Then
 $$ \begin{align*}\dim(G^i) = \prod_{j=1}^m r_{a_{ji}}\text{.} \end{align*} $$
$$ \begin{align*}\dim(G^i) = \prod_{j=1}^m r_{a_{ji}}\text{.} \end{align*} $$
Let us also mention that, with respect to the filtration on
![]() $G^i$
that is induced by the given filtration on V, the slope of
$G^i$
that is induced by the given filtration on V, the slope of
![]() $G^i$
is
$G^i$
is
 $$ \begin{align*}\mu(G^i) = \sum_{j=1}^m \mu(F^{a_{ji}} / F^{a_{ji}-1}) = \sum_{j=1}^m \mu_{a_{ji}} \text{.} \end{align*} $$
$$ \begin{align*}\mu(G^i) = \sum_{j=1}^m \mu(F^{a_{ji}} / F^{a_{ji}-1}) = \sum_{j=1}^m \mu_{a_{ji}} \text{.} \end{align*} $$
(We refer to [Reference Fujimori9, Section 1], for example, for more details about the behavior of slopes under taking tensor products and quotients.)
We next establish isomorphisms
for
![]() $1 \leqslant i \leqslant \ell m$
. The isomorphisms (7.1) are a key point to the proof of Theorem 1.5. Assuming their existence, it then follows that
$1 \leqslant i \leqslant \ell m$
. The isomorphisms (7.1) are a key point to the proof of Theorem 1.5. Assuming their existence, it then follows that
 $$ \begin{align} \dim H^{\# S_{m,z}(\overrightarrow{\mu})} = \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \dim G^i = \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m r_{a_{ji}} \text{.} \end{align} $$
$$ \begin{align} \dim H^{\# S_{m,z}(\overrightarrow{\mu})} = \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \dim G^i = \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m r_{a_{ji}} \text{.} \end{align} $$
The desired conclusion then follows, since, in light of (7.2), it follows that
 $$ \begin{align*}\frac{\dim H^{\# S_{m,z}(\overrightarrow{\mu})}}{\dim V^{\otimes m}} = \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m \frac{r_{a_{ji}}}{r} \text{.} \end{align*} $$
$$ \begin{align*}\frac{\dim H^{\# S_{m,z}(\overrightarrow{\mu})}}{\dim V^{\otimes m}} = \sum_{i=1}^{\# S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m \frac{r_{a_{ji}}}{r} \text{.} \end{align*} $$
However, by (6.1), this may be rewritten as
 $$ \begin{align*}\frac{\dim H^{\# S_{m,z}(\overrightarrow{\mu})}}{\dim V^{\otimes m}} = \sum_{ \mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m \frac{r_{a_j}}{r} = \sum_{ \mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} \text{.} \end{align*} $$
$$ \begin{align*}\frac{\dim H^{\# S_{m,z}(\overrightarrow{\mu})}}{\dim V^{\otimes m}} = \sum_{ \mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m \frac{r_{a_j}}{r} = \sum_{ \mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} \text{.} \end{align*} $$
In particular, it then follows from Theorem 6.1 that
 $$ \begin{align*}\lim_{m \to \infty} \frac{\dim H^{\# S_{m,z} (\overrightarrow{\mu})}}{ \dim V^{\otimes m} } = \lim_{m\to\infty} \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} = 1 \text{.} \end{align*} $$
$$ \begin{align*}\lim_{m \to \infty} \frac{\dim H^{\# S_{m,z} (\overrightarrow{\mu})}}{ \dim V^{\otimes m} } = \lim_{m\to\infty} \sum_{\mathbf{a} \in S_{m,z}(\overrightarrow{\mu})} \prod_{j=1}^m p_{a_j} = 1 \text{.} \end{align*} $$
It remains to establish the isomorphisms (7.1), for each
![]() $1 \leqslant i \leqslant \ell m$
. To this end, we first make note the following vector space isomorphisms:
$1 \leqslant i \leqslant \ell m$
. To this end, we first make note the following vector space isomorphisms:
and
 $$ \begin{align*}G^i \simeq F^i / \left(\sum_{\mathbf{a}_{i} \succ \mathbf{a}_{i'}} F^{i'}\right) \text{;} \end{align*} $$
$$ \begin{align*}G^i \simeq F^i / \left(\sum_{\mathbf{a}_{i} \succ \mathbf{a}_{i'}} F^{i'}\right) \text{;} \end{align*} $$
there is a naturally defined surjection
However, on the other hand,
 $$ \begin{align*}\dim(V^{\otimes m}) = \sum_{i=1}^{\ell m} \dim (H^i / H^{i-1}) \leqslant \sum_{i=1}^{\ell m} \dim G^i \end{align*} $$
$$ \begin{align*}\dim(V^{\otimes m}) = \sum_{i=1}^{\ell m} \dim (H^i / H^{i-1}) \leqslant \sum_{i=1}^{\ell m} \dim G^i \end{align*} $$
and
 $$ \begin{align*}\sum_{i=1}^{\ell m} \dim G^i = \sum_{\mathbf{a}_i = (a_{1i},\dots,a_{mi}) \in [\ell]^m} \left( \prod_{j=1}^m r_{a_{ji}}\right) = \left(\sum_{i=1}^\ell r_i \right)^m = \dim V^{\otimes m} \text{.} \end{align*} $$
$$ \begin{align*}\sum_{i=1}^{\ell m} \dim G^i = \sum_{\mathbf{a}_i = (a_{1i},\dots,a_{mi}) \in [\ell]^m} \left( \prod_{j=1}^m r_{a_{ji}}\right) = \left(\sum_{i=1}^\ell r_i \right)^m = \dim V^{\otimes m} \text{.} \end{align*} $$
The conclusion is then that
 $$ \begin{align*}\dim(V^{\otimes m}) = \sum_{i =1}^{\ell m} \dim G^i \text{;} \end{align*} $$
$$ \begin{align*}\dim(V^{\otimes m}) = \sum_{i =1}^{\ell m} \dim G^i \text{;} \end{align*} $$
whence, by dimension reasons,
for all
![]() $1 \leqslant i \leqslant \ell m$
. The surjections (7.3) and thus injective. The desired isomorphisms (7.1) are thus established.
$1 \leqslant i \leqslant \ell m$
. The surjections (7.3) and thus injective. The desired isomorphisms (7.1) are thus established.
Acknowledgment
This work benefited from a visit to the American Institute of Mathematics during January 2020. I thank Zsolt Patakfalvi for his lecture. Moreover, I thank colleagues for conversations on related topics and for their insightful virtual Zoom lectures. I also thank an anonymous referee for their interest, careful reading of this work, and for providing helpful thoughtful comments.