14 results
3 - Spacetime, Curvature and Gravity
-
- Book:
- The Irresistible Attraction of Gravity
- Published online:
- 02 March 2023
- Print publication:
- 02 March 2023, pp 25-48
-
- Chapter
- Export citation
 $[0,n]\cup \{\omega \}$
IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
$[0,n]\cup \{\omega \}$
IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1632-1656
- Print publication:
- December 2021
-
- Article
- Export citation
Dosimetric verification and quality assurance for intensity-modulated radiation therapy using Gafchromic® EBT3 film
-
- Journal:
- Journal of Radiotherapy in Practice / Volume 17 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 November 2017, pp. 85-95
-
- Article
- Export citation
Proof of de Smit’s conjecture: a freeness criterion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 2310-2317
- Print publication:
- November 2017
-
- Article
- Export citation
Finite Determinacy and Stability of Flatness of Analytic Mappings
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-257
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
À LA RECHERCHE DU TORE PERDU
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 09 March 2016, pp. 1-31
- Print publication:
- March 2016
-
- Article
- Export citation
Output voltage waveform analysis of an intense electron beam accelerator based on strip spiral Blumlein line
-
- Journal:
- Laser and Particle Beams / Volume 30 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 10 July 2012, pp. 379-385
-
- Article
- Export citation
Flat outputs of two-input driftless controlsystems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 14 October 2011, pp. 774-798
- Print publication:
- July 2012
-
- Article
- Export citation
ON HOMOLOGICAL PROPERTIES FOR SOME MODULES OF UNIFORMLY CONTINUOUS FUNCTIONS OVER CONVOLUTION ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 13 July 2011, pp. 177-185
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Homological properties of certain Banach modules over group algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 07 April 2011, pp. 321-328
-
- Article
-
- You have access
- Export citation
Tools for continuous improvement of the plate quenching process*
-
- Journal:
- Revue de Métallurgie – International Journal of Metallurgy / Volume 108 / Issue 5 / 2011
- Published online by Cambridge University Press:
- 19 December 2011, pp. 313-321
- Print publication:
- 2011
-
- Article
- Export citation
Motion planning for a class of boundary controlled linear hyperbolic PDE's involving finite distributed delays
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 9 / January 2003
- Published online by Cambridge University Press:
- 15 September 2003, pp. 419-435
- Print publication:
- January 2003
-
- Article
- Export citation
Motion Planning for a nonlinear Stefan Problem
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 9 / January 2003
- Published online by Cambridge University Press:
- 15 September 2003, pp. 275-296
- Print publication:
- January 2003
-
- Article
- Export citation
FLATTENING AND SUBANALYTIC SETS IN RIGID ANALYTIC GEOMETRY
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 83 / Issue 3 / November 2001
- Published online by Cambridge University Press:
- 18 October 2001, pp. 681-707
- Print publication:
- November 2001
-
- Article
- Export citation


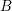
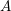
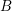
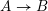
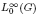 and
and 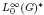 as Banach left
as Banach left 