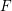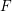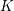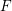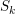2 results
Ascending chain condition for
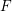 $F$-pure thresholds on a fixed strongly
$F$-pure thresholds on a fixed strongly 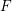 $F$-regular germ
$F$-regular germ
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 28 May 2019, pp. 1194-1223
- Print publication:
- June 2019
-
- Article
- Export citation
F-THRESHOLDS OF GRADED RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 07 December 2016, pp. 141-168
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation