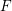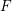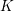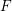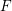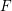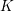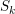1 Introduction
Throughout this manuscript we focus on
![]() $F$
-pure standard graded algebras over a field
$F$
-pure standard graded algebras over a field
![]() $K$
of positive characteristic
$K$
of positive characteristic
![]() $p$
such that
$p$
such that
![]() $[K:K^{p}]<\infty$
. We say that
$[K:K^{p}]<\infty$
. We say that
![]() $R$
is
$R$
is
![]() $F$
-pure if the Frobenius map
$F$
-pure if the Frobenius map
![]() $F:R\rightarrow R$
splits. This property simplifies computations for cohomology groups and implies vanishing properties of these groups [Reference LyubeznikLyu06, Reference Singh and WaltherSW07, Reference MaMa13].
$F:R\rightarrow R$
splits. This property simplifies computations for cohomology groups and implies vanishing properties of these groups [Reference LyubeznikLyu06, Reference Singh and WaltherSW07, Reference MaMa13].
In this article, we show relations among three important classes of invariants that give information about the singularity of
![]() $R$
: the
$R$
: the
![]() $a$
-invariants, the
$a$
-invariants, the
![]() $F$
-pure threshold, and the diagonal
$F$
-pure threshold, and the diagonal
![]() $F$
-threshold.
$F$
-threshold.
We first consider the
![]() $i$
th
$i$
th
![]() $a$
-invariant of
$a$
-invariant of
![]() $R,$
$R,$
![]() $a_{i}(R)$
, which is defined as the degree of the highest nonzero part of the
$a_{i}(R)$
, which is defined as the degree of the highest nonzero part of the
![]() $i$
th local cohomology with support over
$i$
th local cohomology with support over
![]() $\mathfrak{m}$
(see Section 2 for details). If
$\mathfrak{m}$
(see Section 2 for details). If
![]() $d=\dim (R)$
, then
$d=\dim (R)$
, then
![]() $a_{d}(R)$
is often just called the
$a_{d}(R)$
is often just called the
![]() $a$
-invariant of
$a$
-invariant of
![]() $R$
, and it is a classical invariant, introduced by Goto and Watanabe [Reference Goto and WatanabeGW78]. For example, if
$R$
, and it is a classical invariant, introduced by Goto and Watanabe [Reference Goto and WatanabeGW78]. For example, if
![]() $R$
is Cohen–Macaulay,
$R$
is Cohen–Macaulay,
![]() $a_{d}(R)$
determines the highest shift in the resolution of
$a_{d}(R)$
determines the highest shift in the resolution of
![]() $R$
, and moreover the Hilbert function and the Hilbert polynomial of
$R$
, and moreover the Hilbert function and the Hilbert polynomial of
![]() $R$
coincide if and only if
$R$
coincide if and only if
![]() $a_{d}(R)$
is negative.
$a_{d}(R)$
is negative.
We also consider the
![]() $F$
-pure threshold with respect to
$F$
-pure threshold with respect to
![]() $\mathfrak{m}$
,
$\mathfrak{m}$
,
![]() $\operatorname{fpt}(R)$
, which was introduced by Takagi and Watanabe [Reference Takagi and WatanabeTW04] (see Section 3 for details). This invariant is related to the log-canonical threshold and roughly speaking measures the asymptotic splitting order of
$\operatorname{fpt}(R)$
, which was introduced by Takagi and Watanabe [Reference Takagi and WatanabeTW04] (see Section 3 for details). This invariant is related to the log-canonical threshold and roughly speaking measures the asymptotic splitting order of
![]() $\mathfrak{m}.$
$\mathfrak{m}.$
Finally, we consider the diagonal
![]() $F$
-threshold,
$F$
-threshold,
![]() $c^{\mathfrak{m}}(R)$
. This invariant is, roughly speaking, the asymptotic Frobenius order of
$c^{\mathfrak{m}}(R)$
. This invariant is, roughly speaking, the asymptotic Frobenius order of
![]() $\mathfrak{m}$
, and it has several connections with tight closure theory [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08]. The
$\mathfrak{m}$
, and it has several connections with tight closure theory [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08]. The
![]() $F$
-threshold has also connections with the Hilbert–Samuel multiplicity [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08] and with the Hilbert Kunz multiplicity [Reference Núñez-Betancourt and SmirnovNBS14].
$F$
-threshold has also connections with the Hilbert–Samuel multiplicity [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08] and with the Hilbert Kunz multiplicity [Reference Núñez-Betancourt and SmirnovNBS14].
Hirose, Watanabe, and Yoshida [Reference Hirose, Watanabe and YoshidaHWY14] made the following conjecture that relates these invariants:
Conjecture A. [Reference Hirose, Watanabe and YoshidaHWY14]
Let
![]() $R$
be a standard graded
$R$
be a standard graded
![]() $K$
-algebra with
$K$
-algebra with
![]() $K$
an
$K$
an
![]() $F$
-finite field and
$F$
-finite field and
![]() $d=\dim (R)$
. Assume that
$d=\dim (R)$
. Assume that
![]() $R$
is strongly
$R$
is strongly
![]() $F$
-regular. Then,
$F$
-regular. Then,
-
(1)
 $\operatorname{fpt}(R)\leqslant -a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
.
$\operatorname{fpt}(R)\leqslant -a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
. -
(2)
 $\operatorname{fpt}(R)=-a_{d}(R)$
if and only if
$\operatorname{fpt}(R)=-a_{d}(R)$
if and only if
 $R$
is Gorenstein.
$R$
is Gorenstein.
This conjecture has been proved only for strongly
![]() $F$
-regular Hibi rings [Reference Chiba and MatsudaCM12] and affine toric rings [Reference Hirose, Watanabe and YoshidaHWY14]. In addition,
$F$
-regular Hibi rings [Reference Chiba and MatsudaCM12] and affine toric rings [Reference Hirose, Watanabe and YoshidaHWY14]. In addition,
![]() $\operatorname{fpt}(R)=-a_{d}(R)$
for strongly
$\operatorname{fpt}(R)=-a_{d}(R)$
for strongly
![]() $F$
-regular standard graded Gorenstein rings [Reference Takagi and WatanabeTW04, Example 2.4(iv)]. In this paper we settle the first part of this conjecture and one direction of the second. Furthermore, we drop the restrictive hypotheses of strong
$F$
-regular standard graded Gorenstein rings [Reference Takagi and WatanabeTW04, Example 2.4(iv)]. In this paper we settle the first part of this conjecture and one direction of the second. Furthermore, we drop the restrictive hypotheses of strong
![]() $F$
-regularity. We just assume that
$F$
-regularity. We just assume that
![]() $R$
is
$R$
is
![]() $F$
-pure, which is needed to define
$F$
-pure, which is needed to define
![]() $\operatorname{fpt}(R)$
.
$\operatorname{fpt}(R)$
.
Theorem B. (See Theorems 4.3, 4.9, and 5.2)
Let
![]() $R$
be a standard graded
$R$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure, and let
$F$
-pure, and let
![]() $d=\dim (R)$
. Then,
$d=\dim (R)$
. Then,
-
(1)
 $\operatorname{fpt}(R)\leqslant -a_{i}(R)$
for every
$\operatorname{fpt}(R)\leqslant -a_{i}(R)$
for every
 $i\in \mathbb{N}$
.
$i\in \mathbb{N}$
. -
(2) If
 $a_{i}(R)\neq -\infty ,$
then
$a_{i}(R)\neq -\infty ,$
then
 $-a_{i}(R)\leqslant c^{\mathfrak{m}}(R)$
.
$-a_{i}(R)\leqslant c^{\mathfrak{m}}(R)$
. -
(3) If
 $R$
is Gorenstein, then
$R$
is Gorenstein, then
 $\operatorname{fpt}(R)=-a_{d}(R).$
$\operatorname{fpt}(R)=-a_{d}(R).$
Theorem B(2) implies that
![]() $-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
for standard graded
$-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
for standard graded
![]() $F$
-pure
$F$
-pure
![]() $K$
-algebras. This inequality has been proven before for complete intersections without assuming strongly
$K$
-algebras. This inequality has been proven before for complete intersections without assuming strongly
![]() $F$
-regularity or
$F$
-regularity or
![]() $F$
-purity [Reference LiLi13, Proposition 2.3]. In Theorem 4.9, we prove
$F$
-purity [Reference LiLi13, Proposition 2.3]. In Theorem 4.9, we prove
![]() $-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
for all
$-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
for all
![]() $F$
-finite standard graded
$F$
-finite standard graded
![]() $K$
-algebras. In Example 5.3, we show that the converse of Theorem B(3) does not hold in general. This does not disprove Conjecture A(2), since the ring that we consider is not strongly
$K$
-algebras. In Example 5.3, we show that the converse of Theorem B(3) does not hold in general. This does not disprove Conjecture A(2), since the ring that we consider is not strongly
![]() $F$
-regular.
$F$
-regular.
We also prove the analogue of Conjecture A(1) in characteristic zero, and we show one direction of Conjecture A(2). These results are obtained by reduction to positive characteristic methods [Reference Hochster and HunekeHH99].
Theorem C. (See Theorem 6.8)
Let
![]() $K$
be a field of characteristic zero, and let
$K$
be a field of characteristic zero, and let
![]() $(R,\mathfrak{m},K)$
be a standard graded normal and
$(R,\mathfrak{m},K)$
be a standard graded normal and
![]() $\mathbb{Q}$
-Gorenstein
$\mathbb{Q}$
-Gorenstein
![]() $K$
-algebra such that
$K$
-algebra such that
![]() $X=\operatorname{Spec}R$
is log-terminal. Let
$X=\operatorname{Spec}R$
is log-terminal. Let
![]() $d=\dim (R)$
. Then,
$d=\dim (R)$
. Then,
-
(1)
 $\operatorname{lct}(X)\leqslant -a_{d}(R)$
.
$\operatorname{lct}(X)\leqslant -a_{d}(R)$
. -
(2) If
 $R$
is Gorenstein, then
$R$
is Gorenstein, then
 $\operatorname{lct}(X)=-a_{d}(R).$
$\operatorname{lct}(X)=-a_{d}(R).$
Furthermore, we give a new interpretation of
![]() $\operatorname{fpt}(R)$
for Gorenstein standard graded
$\operatorname{fpt}(R)$
for Gorenstein standard graded
![]() $K$
-algebras in terms of regular sequences that preserve
$K$
-algebras in terms of regular sequences that preserve
![]() $F$
-purity. We call such a sequence an
$F$
-purity. We call such a sequence an
![]() $F$
-pure regular sequence (see Definition 5.5).
$F$
-pure regular sequence (see Definition 5.5).
Theorem D. (See Theorem 5.8)
Let
![]() $(R,\mathfrak{m},K)$
be a Gorenstein standard graded
$(R,\mathfrak{m},K)$
be a Gorenstein standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure over an infinite field. Let
$F$
-pure over an infinite field. Let
![]() $d=\dim (R)$
, and let
$d=\dim (R)$
, and let
![]() $s=\operatorname{fpt}(R)$
. Then, there exists a regular sequence consisting of
$s=\operatorname{fpt}(R)$
. Then, there exists a regular sequence consisting of
![]() $s$
linear forms
$s$
linear forms
![]() $\ell _{1},\ldots ,\ell _{s}$
such that
$\ell _{1},\ldots ,\ell _{s}$
such that
![]() $R/(\ell _{1},\ldots ,\ell _{j})$
is
$R/(\ell _{1},\ldots ,\ell _{j})$
is
![]() $F$
-pure for every
$F$
-pure for every
![]() $j=1,\ldots ,s$
.
$j=1,\ldots ,s$
.
Theorem 5.8 is in the spirit of Bertini type theorems and ladders on Fano varieties [Reference AmbroAmb99]. These theorems assert that ‘nice’ singularities are still ‘good’ after cutting by a general hyperplane. Among these nice singularities one encounters
![]() $F$
-pure singularities of a projective variety [Reference Schwede and ZhangSZ13]. Theorem 5.8 gives a number of successive hyperplane cuts in
$F$
-pure singularities of a projective variety [Reference Schwede and ZhangSZ13]. Theorem 5.8 gives a number of successive hyperplane cuts in
![]() $\operatorname{Proj}(R)$
that preserve
$\operatorname{Proj}(R)$
that preserve
![]() $F$
-purity. Furthermore, the hyperplane cuts remain globally
$F$
-purity. Furthermore, the hyperplane cuts remain globally
![]() $F$
-pure.
$F$
-pure.
Finally, we give explicit bounds for the projective dimension and the Castelnuovo–Mumford regularity of
![]() $R=S/I$
, where
$R=S/I$
, where
![]() $S=K[x_{1},\ldots ,x_{n}]$
is a polynomial ring over a field of positive characteristic, and
$S=K[x_{1},\ldots ,x_{n}]$
is a polynomial ring over a field of positive characteristic, and
![]() $I\subseteq S$
is a homogeneous ideal such that
$I\subseteq S$
is a homogeneous ideal such that
![]() $R$
is
$R$
is
![]() $F$
-pure (see Theorem 7.3). In addition, we show that if an
$F$
-pure (see Theorem 7.3). In addition, we show that if an
![]() $F$
-pure standard graded
$F$
-pure standard graded
![]() $K$
-algebra
$K$
-algebra
![]() $R=S/I$
satisfies Serre’s
$R=S/I$
satisfies Serre’s
![]() $S_{k}$
condition, for some
$S_{k}$
condition, for some
![]() $k$
depending on the degrees of the generators of
$k$
depending on the degrees of the generators of
![]() $I$
, then
$I$
, then
![]() $R$
is in fact Cohen–Macaulay (see Proposition 7.6).
$R$
is in fact Cohen–Macaulay (see Proposition 7.6).
2 Background
Throughout this article,
![]() $R$
denotes a commutative Noetherian ring with identity. A positively graded ring is a ring which admits a decomposition
$R$
denotes a commutative Noetherian ring with identity. A positively graded ring is a ring which admits a decomposition
![]() $R=\bigoplus _{i\geqslant 0}R_{i}$
of abelian groups, with
$R=\bigoplus _{i\geqslant 0}R_{i}$
of abelian groups, with
![]() $R_{i}\cdot R_{j}\subseteq R_{i+j}$
for all
$R_{i}\cdot R_{j}\subseteq R_{i+j}$
for all
![]() $i$
and
$i$
and
![]() $j$
. A standard graded ring is a positively graded ring such that
$j$
. A standard graded ring is a positively graded ring such that
![]() $R_{0}=K$
is a field,
$R_{0}=K$
is a field,
![]() $R=K[R_{1}]$
and
$R=K[R_{1}]$
and
![]() $\dim _{K}(R_{1})<\infty$
, that is,
$\dim _{K}(R_{1})<\infty$
, that is,
![]() $R$
is a finitely generated
$R$
is a finitely generated
![]() $K$
-algebra, generated in degree one. We use the notation
$K$
-algebra, generated in degree one. We use the notation
![]() $(R,\mathfrak{m},K)$
to denote a standard graded
$(R,\mathfrak{m},K)$
to denote a standard graded
![]() $K$
-algebra, where
$K$
-algebra, where
![]() $\mathfrak{m}=\bigoplus _{i\geqslant 1}R_{i}$
is the irrelevant maximal ideal.
$\mathfrak{m}=\bigoplus _{i\geqslant 1}R_{i}$
is the irrelevant maximal ideal.
Suppose that
![]() $R$
is a standard graded
$R$
is a standard graded
![]() $K$
-algebra. A graded module is an
$K$
-algebra. A graded module is an
![]() $R$
-module
$R$
-module
![]() $M=\bigoplus _{n\in \mathbb{Z}}M_{n}$
such that
$M=\bigoplus _{n\in \mathbb{Z}}M_{n}$
such that
![]() $R_{i}M_{j}\subseteq M_{i+j}$
. An
$R_{i}M_{j}\subseteq M_{i+j}$
. An
![]() $R$
-homomorphism
$R$
-homomorphism
![]() $\unicode[STIX]{x1D711}:M\rightarrow N$
between graded
$\unicode[STIX]{x1D711}:M\rightarrow N$
between graded
![]() $R$
-modules is called homogeneous of degree
$R$
-modules is called homogeneous of degree
![]() $c$
if
$c$
if
![]() $\unicode[STIX]{x1D711}(M_{i})\subseteq N_{i+c}$
for all
$\unicode[STIX]{x1D711}(M_{i})\subseteq N_{i+c}$
for all
![]() $i\in \mathbb{Z}$
. The set of all graded homomorphisms
$i\in \mathbb{Z}$
. The set of all graded homomorphisms
![]() $M\rightarrow N$
of all degrees form a graded submodule of
$M\rightarrow N$
of all degrees form a graded submodule of
![]() $\operatorname{Hom}_{R}(M,N)$
. In general, these two modules are not the same, but they coincide when
$\operatorname{Hom}_{R}(M,N)$
. In general, these two modules are not the same, but they coincide when
![]() $M$
is finitely generated [Reference Bruns and HerzogBH93]. Throughout this article,
$M$
is finitely generated [Reference Bruns and HerzogBH93]. Throughout this article,
![]() $E_{R}(K)$
will denote the graded
$E_{R}(K)$
will denote the graded
![]() $R$
-module
$R$
-module
![]() $\bigoplus _{i\in \mathbb{Z}}\operatorname{Hom}_{K}(R_{-i},K)$
.
$\bigoplus _{i\in \mathbb{Z}}\operatorname{Hom}_{K}(R_{-i},K)$
.
Let
![]() $I$
be a homogeneous ideal generated by the forms
$I$
be a homogeneous ideal generated by the forms
![]() $f_{1},\ldots ,f_{\ell }\in R$
. Consider the
$f_{1},\ldots ,f_{\ell }\in R$
. Consider the
![]() $\check{\text{C}}$
ech complex,
$\check{\text{C}}$
ech complex,
![]() $\check{\text{C}}^{\bullet }(\text{}\underline{f};R)$
:
$\check{\text{C}}^{\bullet }(\text{}\underline{f};R)$
:
where
![]() $\check{\text{C}}^{i}(\text{}\underline{f};R)=\bigoplus _{1\leqslant j_{1}<\cdots <j_{i}\leqslant \ell }R_{f_{j_{1}}\cdots f_{j_{i}}}$
and the homomorphism in every summand is a localization map with an appropriate sign. Let
$\check{\text{C}}^{i}(\text{}\underline{f};R)=\bigoplus _{1\leqslant j_{1}<\cdots <j_{i}\leqslant \ell }R_{f_{j_{1}}\cdots f_{j_{i}}}$
and the homomorphism in every summand is a localization map with an appropriate sign. Let
![]() $M$
be a graded
$M$
be a graded
![]() $R$
-module. We define the
$R$
-module. We define the
![]() $i$
-th local cohomology of
$i$
-th local cohomology of
![]() $M$
with support in
$M$
with support in
![]() $I$
by
$I$
by
![]() $H_{I}^{i}(M):=H^{i}(\check{\text{C}}^{\bullet }(\text{}\underline{f};R)\otimes _{R}M)$
. The local cohomology module
$H_{I}^{i}(M):=H^{i}(\check{\text{C}}^{\bullet }(\text{}\underline{f};R)\otimes _{R}M)$
. The local cohomology module
![]() $H_{I}^{i}(M)$
does not depend on the choice of generators,
$H_{I}^{i}(M)$
does not depend on the choice of generators,
![]() $f_{1},\ldots ,f_{\ell }$
, of
$f_{1},\ldots ,f_{\ell }$
, of
![]() $I$
. Moreover, it only depends on the radical of
$I$
. Moreover, it only depends on the radical of
![]() $I$
. Since
$I$
. Since
![]() $M$
is a graded
$M$
is a graded
![]() $R$
-module and
$R$
-module and
![]() $I$
is homogeneous, the
$I$
is homogeneous, the
![]() $i$
th local cohomology
$i$
th local cohomology
![]() $H_{I}^{i}(M)$
is graded as well. Furthermore, if
$H_{I}^{i}(M)$
is graded as well. Furthermore, if
![]() $\unicode[STIX]{x1D711}:M\rightarrow N$
is a homogeneous
$\unicode[STIX]{x1D711}:M\rightarrow N$
is a homogeneous
![]() $R$
-module homomorphism of degree
$R$
-module homomorphism of degree
![]() $d$
, then the induced
$d$
, then the induced
![]() $R$
-module map
$R$
-module map
![]() $H_{I}^{i}(M)\rightarrow H_{I}^{i}(N)$
is homogeneous of degree
$H_{I}^{i}(M)\rightarrow H_{I}^{i}(N)$
is homogeneous of degree
![]() $d$
as well.
$d$
as well.
Assume that
![]() $R$
has positive characteristic
$R$
has positive characteristic
![]() $p$
. For
$p$
. For
![]() $e\in \mathbb{N}$
, let
$e\in \mathbb{N}$
, let
![]() $F^{e}:R\rightarrow R$
denote the
$F^{e}:R\rightarrow R$
denote the
![]() $e$
th iteration of the Frobenius endomorphism on
$e$
th iteration of the Frobenius endomorphism on
![]() $R$
. If
$R$
. If
![]() $R$
is reduced,
$R$
is reduced,
![]() $R^{1/p^{e}}$
denotes the ring of
$R^{1/p^{e}}$
denotes the ring of
![]() $p^{e}$
th roots of
$p^{e}$
th roots of
![]() $R$
and we can identify
$R$
and we can identify
![]() $F^{e}$
with the inclusion
$F^{e}$
with the inclusion
![]() $R\subseteq R^{1/p^{e}}$
. When
$R\subseteq R^{1/p^{e}}$
. When
![]() $R$
is standard graded, we view
$R$
is standard graded, we view
![]() $R^{1/p^{e}}$
as a
$R^{1/p^{e}}$
as a
![]() $1/p^{e}\mathbb{N}$
-graded module. In fact, if
$1/p^{e}\mathbb{N}$
-graded module. In fact, if
![]() $r^{1/p^{e}}\in R^{1/p^{e}}$
, then we write
$r^{1/p^{e}}\in R^{1/p^{e}}$
, then we write
![]() $r\in R$
as
$r\in R$
as
![]() $r=r_{d_{1}}+\cdots +r_{d_{n}}$
, with
$r=r_{d_{1}}+\cdots +r_{d_{n}}$
, with
![]() $r_{d_{j}}\in R_{d_{j}}$
. Then
$r_{d_{j}}\in R_{d_{j}}$
. Then
![]() $r^{1/p^{e}}=r_{d_{1}}^{1/p^{e}}+\cdots +r_{d_{n}}^{1/p^{e}}$
, and each
$r^{1/p^{e}}=r_{d_{1}}^{1/p^{e}}+\cdots +r_{d_{n}}^{1/p^{e}}$
, and each
![]() $r_{d_{j}}^{1/p^{e}}$
has degree
$r_{d_{j}}^{1/p^{e}}$
has degree
![]() $d_{j}/p^{e}$
. Similarly, if
$d_{j}/p^{e}$
. Similarly, if
![]() $M$
is a
$M$
is a
![]() $\mathbb{Z}$
-graded
$\mathbb{Z}$
-graded
![]() $R$
-module, we have that
$R$
-module, we have that
![]() $M^{1/p^{e}}$
is a
$M^{1/p^{e}}$
is a
![]() $1/p^{e}\mathbb{Z}$
-graded
$1/p^{e}\mathbb{Z}$
-graded
![]() $R$
-module. Here
$R$
-module. Here
![]() $M^{1/p^{e}}$
denotes the
$M^{1/p^{e}}$
denotes the
![]() $R$
-module which has the same additive structure as
$R$
-module which has the same additive structure as
![]() $M$
, and multiplication defined by
$M$
, and multiplication defined by
![]() $r\cdot m^{1/p^{e}}:=(r^{p^{e}}m)^{1/p^{e}}$
for all
$r\cdot m^{1/p^{e}}:=(r^{p^{e}}m)^{1/p^{e}}$
for all
![]() $r\in R$
and
$r\in R$
and
![]() $m^{1/p^{e}}\in M^{1/p^{e}}$
.
$m^{1/p^{e}}\in M^{1/p^{e}}$
.
Remark 2.1. When
![]() $R$
is reduced, for any integer
$R$
is reduced, for any integer
![]() $e\geqslant 1$
we have an inclusion
$e\geqslant 1$
we have an inclusion
![]() $R{\hookrightarrow}R^{1/p^{e}}$
. As a submodule of
$R{\hookrightarrow}R^{1/p^{e}}$
. As a submodule of
![]() $R^{1/p^{e}}$
,
$R^{1/p^{e}}$
,
![]() $R$
inherits a natural
$R$
inherits a natural
![]() $1/p^{e}\mathbb{N}$
grading, which is compatible with the standard grading.
$1/p^{e}\mathbb{N}$
grading, which is compatible with the standard grading.
If
![]() $\sqrt{I}=\mathfrak{m}$
and
$\sqrt{I}=\mathfrak{m}$
and
![]() $M$
is finitely generated, the modules
$M$
is finitely generated, the modules
![]() $H_{\mathfrak{m}}^{i}(M)$
are Artinian. Therefore, the following numbers are well defined.
$H_{\mathfrak{m}}^{i}(M)$
are Artinian. Therefore, the following numbers are well defined.
Definition 2.2. Let
![]() $M$
be a
$M$
be a
![]() $1/p^{e}\mathbb{N}$
-graded finitely generated
$1/p^{e}\mathbb{N}$
-graded finitely generated
![]() $R$
-module. For
$R$
-module. For
![]() $i\in \mathbb{N}$
, if
$i\in \mathbb{N}$
, if
![]() $H_{\mathfrak{m}}^{i}(M)\neq 0$
then the
$H_{\mathfrak{m}}^{i}(M)\neq 0$
then the
![]() $a_{i}$
-invariant of
$a_{i}$
-invariant of
![]() $M$
is defined as
$M$
is defined as
If
![]() $H_{\mathfrak{m}}^{i}(M)=0$
, we set
$H_{\mathfrak{m}}^{i}(M)=0$
, we set
![]() $a_{i}(M):=-\infty$
.
$a_{i}(M):=-\infty$
.
Remark 2.3. With the grading introduced above, for a finitely generated graded
![]() $R$
-module,
$R$
-module,
![]() $M$
, we have that
$M$
, we have that
![]() $a_{i}(M^{1/p^{e}})=a_{i}(M)/p^{e}$
for all
$a_{i}(M^{1/p^{e}})=a_{i}(M)/p^{e}$
for all
![]() $i\in \mathbb{N}$
. In fact,
$i\in \mathbb{N}$
. In fact,
![]() $H_{\mathfrak{m}}^{i}(M^{1/p^{e}})\cong H_{\mathfrak{m}}^{i}(M)^{1/p^{e}}$
since the functor
$H_{\mathfrak{m}}^{i}(M^{1/p^{e}})\cong H_{\mathfrak{m}}^{i}(M)^{1/p^{e}}$
since the functor
![]() $(-)^{1/p^{e}}$
is exact.
$(-)^{1/p^{e}}$
is exact.
Definition 2.4. Let
![]() $R$
be a Noetherian ring of positive characteristic
$R$
be a Noetherian ring of positive characteristic
![]() $p$
. We say that
$p$
. We say that
![]() $R$
is
$R$
is
![]() $F$
-finite if it is a finitely generated
$F$
-finite if it is a finitely generated
![]() $R$
-module via the action induced by the Frobenius endomorphism
$R$
-module via the action induced by the Frobenius endomorphism
![]() $F:R\rightarrow R$
. When
$F:R\rightarrow R$
. When
![]() $R$
is reduced, this is equivalent to say that
$R$
is reduced, this is equivalent to say that
![]() $R^{1/p}$
is a finitely generated
$R^{1/p}$
is a finitely generated
![]() $R$
-module. If
$R$
-module. If
![]() $(R,\mathfrak{m},K)$
is a standard graded
$(R,\mathfrak{m},K)$
is a standard graded
![]() $K$
-algebra, then
$K$
-algebra, then
![]() $R$
is
$R$
is
![]() $F$
-finite if and only if
$F$
-finite if and only if
![]() $K$
is
$K$
is
![]() $F$
-finite, that is, if and only if
$F$
-finite, that is, if and only if
![]() $[K:K^{p}]<\infty$
.
$[K:K^{p}]<\infty$
.
![]() $R$
is called
$R$
is called
![]() $F$
-pure if
$F$
-pure if
![]() $F$
is a pure homomorphism, that is
$F$
is a pure homomorphism, that is
![]() $F\otimes 1:R\otimes _{R}M\rightarrow R\otimes _{R}M$
is injective for all
$F\otimes 1:R\otimes _{R}M\rightarrow R\otimes _{R}M$
is injective for all
![]() $R$
-modules
$R$
-modules
![]() $M$
.
$M$
.
![]() $R$
is called
$R$
is called
![]() $F$
-split if
$F$
-split if
![]() $F$
is a split monomorphism.
$F$
is a split monomorphism.
Remark 2.5. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $F$
-pure
$F$
-pure
![]() $K$
-algebra. Then necessarily
$K$
-algebra. Then necessarily
![]() $a_{i}(R)\leqslant 0$
for all
$a_{i}(R)\leqslant 0$
for all
![]() $i\in \mathbb{Z}$
[Reference Hochster and RobertsHR76, Proposition 2.4].
$i\in \mathbb{Z}$
[Reference Hochster and RobertsHR76, Proposition 2.4].
Remark 2.6. If
![]() $R$
is an
$R$
is an
![]() $F$
-pure ring,
$F$
-pure ring,
![]() $F$
itself is injective and
$F$
itself is injective and
![]() $R$
must be a reduced ring. We have that
$R$
must be a reduced ring. We have that
![]() $R$
is
$R$
is
![]() $F$
-split if and only if
$F$
-split if and only if
![]() $R$
is a direct summand of
$R$
is a direct summand of
![]() $R^{1/p}$
. If
$R^{1/p}$
. If
![]() $R$
is an
$R$
is an
![]() $F$
-finite ring,
$F$
-finite ring,
![]() $R$
is
$R$
is
![]() $F$
-pure if and only
$F$
-pure if and only
![]() $R$
is
$R$
is
![]() $F$
-split (see [Reference Hochster and RobertsHR76, Corollary
$F$
-split (see [Reference Hochster and RobertsHR76, Corollary
![]() $5.3$
]). Since, throughout this article, we assume that
$5.3$
]). Since, throughout this article, we assume that
![]() $R$
is
$R$
is
![]() $F$
-finite, we use the word
$F$
-finite, we use the word
![]() $F$
-pure to refer to both.
$F$
-pure to refer to both.
Definition 2.7. An
![]() $F$
-finite reduced ring
$F$
-finite reduced ring
![]() $R$
is strongly
$R$
is strongly
![]() $F$
-regular if for any element
$F$
-regular if for any element
![]() $f\in R\setminus \{0\}$
, there exists
$f\in R\setminus \{0\}$
, there exists
![]() $e\in \mathbb{N}$
such that the inclusion
$e\in \mathbb{N}$
such that the inclusion
![]() $f^{1/p^{e}}R\rightarrow R^{1/p^{e}}$
splits.
$f^{1/p^{e}}R\rightarrow R^{1/p^{e}}$
splits.
Definition 2.8. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
![]() $F$
-finite field. The
$F$
-finite field. The
![]() $e$
-trace map,
$e$
-trace map,
![]() $\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S,$
is defined by
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S,$
is defined by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F7}_{e}(x_{1}^{\unicode[STIX]{x1D6FC}_{1}/p^{e}}\cdots x_{n}^{\unicode[STIX]{x1D6FC}_{n}/p^{e}})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}\displaystyle x_{1}^{(\unicode[STIX]{x1D6FC}_{1}-p^{e}+1)/p^{e}}\cdots x_{n}^{(\unicode[STIX]{x1D6FC}_{n}-p^{e}+1)/p^{e}}\quad & \displaystyle \unicode[STIX]{x1D6FC}_{1}\equiv \cdots \equiv \unicode[STIX]{x1D6FC}_{n}\equiv p^{e}-1\text{ mod }p^{e},\\ \displaystyle 0\quad & \displaystyle \text{otherwise}.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F7}_{e}(x_{1}^{\unicode[STIX]{x1D6FC}_{1}/p^{e}}\cdots x_{n}^{\unicode[STIX]{x1D6FC}_{n}/p^{e}})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}\displaystyle x_{1}^{(\unicode[STIX]{x1D6FC}_{1}-p^{e}+1)/p^{e}}\cdots x_{n}^{(\unicode[STIX]{x1D6FC}_{n}-p^{e}+1)/p^{e}}\quad & \displaystyle \unicode[STIX]{x1D6FC}_{1}\equiv \cdots \equiv \unicode[STIX]{x1D6FC}_{n}\equiv p^{e}-1\text{ mod }p^{e},\\ \displaystyle 0\quad & \displaystyle \text{otherwise}.\end{array}\right.\nonumber\end{eqnarray}$$
We note that
![]() $\unicode[STIX]{x1D6F7}_{e^{\prime }}\circ \unicode[STIX]{x1D6F7}_{e}^{1/p^{e^{\prime }}}=\unicode[STIX]{x1D6F7}_{e^{\prime }+e}$
. Furthermore,
$\unicode[STIX]{x1D6F7}_{e^{\prime }}\circ \unicode[STIX]{x1D6F7}_{e}^{1/p^{e^{\prime }}}=\unicode[STIX]{x1D6F7}_{e^{\prime }+e}$
. Furthermore,
![]() $\unicode[STIX]{x1D6F7}_{e}$
generates
$\unicode[STIX]{x1D6F7}_{e}$
generates
![]() $\operatorname{Hom}_{S}(S^{1/p^{e}},S)$
as an
$\operatorname{Hom}_{S}(S^{1/p^{e}},S)$
as an
![]() $S^{1/p^{e}}$
-module.
$S^{1/p^{e}}$
-module.
Definition 2.9. [Reference SchwedeSch10]
Suppose that
![]() $R$
is an
$R$
is an
![]() $F$
-pure ring. Let
$F$
-pure ring. Let
![]() $\unicode[STIX]{x1D719}:R^{1/p^{e}}\rightarrow R$
be an
$\unicode[STIX]{x1D719}:R^{1/p^{e}}\rightarrow R$
be an
![]() $R$
-homomorphism and let
$R$
-homomorphism and let
![]() $J\subseteq R$
be an ideal. We say that
$J\subseteq R$
be an ideal. We say that
![]() $J$
is
$J$
is
![]() $\unicode[STIX]{x1D719}$
-compatible if
$\unicode[STIX]{x1D719}$
-compatible if
![]() $\unicode[STIX]{x1D719}(J^{1/p^{e}})\subseteq J$
. An ideal
$\unicode[STIX]{x1D719}(J^{1/p^{e}})\subseteq J$
. An ideal
![]() $J$
is said to be compatible if it is
$J$
is said to be compatible if it is
![]() $\unicode[STIX]{x1D719}$
-compatible for all
$\unicode[STIX]{x1D719}$
-compatible for all
![]() $R$
-linear maps
$R$
-linear maps
![]() $\unicode[STIX]{x1D719}:R^{1/p^{e}}\rightarrow R$
and all
$\unicode[STIX]{x1D719}:R^{1/p^{e}}\rightarrow R$
and all
![]() $e\in \mathbb{N}$
.
$e\in \mathbb{N}$
.
We end this section by recalling an explicit description of
![]() $\operatorname{Hom}_{R}(R^{1/p^{e}},R)$
discovered by Fedder [Reference FedderFed83] that we use in the following sections.
$\operatorname{Hom}_{R}(R^{1/p^{e}},R)$
discovered by Fedder [Reference FedderFed83] that we use in the following sections.
Remark 2.10. [Reference FedderFed83, Corollary 1.5]
Let
![]() $S$
be a polynomial ring over an
$S$
be a polynomial ring over an
![]() $F$
-finite field, and let
$F$
-finite field, and let
![]() $\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
be the trace map. Let
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
be the trace map. Let
![]() $I\subseteq S$
be a homogeneous ideal, and let
$I\subseteq S$
be a homogeneous ideal, and let
![]() $R=S/I$
. We have a graded isomorphism
$R=S/I$
. We have a graded isomorphism
given by the correspondence
![]() $f^{1/p^{e}}\mapsto \unicode[STIX]{x1D711}_{f,e}$
, where
$f^{1/p^{e}}\mapsto \unicode[STIX]{x1D711}_{f,e}$
, where
![]() $\unicode[STIX]{x1D711}_{f,e}:R^{1/p^{e}}\rightarrow R$
is defined by
$\unicode[STIX]{x1D711}_{f,e}:R^{1/p^{e}}\rightarrow R$
is defined by
![]() $\unicode[STIX]{x1D711}_{f,e}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r)}.$
$\unicode[STIX]{x1D711}_{f,e}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r)}.$
Thanks to the correspondence in Remark 2.10, we can make the following observation.
Remark 2.11. Let
![]() $S$
be a polynomial ring over an
$S$
be a polynomial ring over an
![]() $F$
-finite field. Let
$F$
-finite field. Let
![]() $I\subseteq S$
be a homogeneous ideal, and let
$I\subseteq S$
be a homogeneous ideal, and let
![]() $R=S/I$
. Let
$R=S/I$
. Let
![]() $J\subseteq R$
be a homogeneous ideal, and let
$J\subseteq R$
be a homogeneous ideal, and let
![]() $\widetilde{J}$
denote its pullback to
$\widetilde{J}$
denote its pullback to
![]() $S$
. We have that
$S$
. We have that
![]() $J$
is compatible if and only if
$J$
is compatible if and only if
![]() $(I^{[p^{e}]}:I)\subseteq (\widetilde{J}^{[p^{e}]}:\widetilde{J})$
for all
$(I^{[p^{e}]}:I)\subseteq (\widetilde{J}^{[p^{e}]}:\widetilde{J})$
for all
![]() $e\geqslant 1$
.
$e\geqslant 1$
.
3 Properties of
 $F$
-thresholds
$F$
-thresholds
In this section we introduce basic definitions and properties for the diagonal
![]() $F$
-threshold and the
$F$
-threshold and the
![]() $F$
-pure threshold.
$F$
-pure threshold.
Definition 3.1. [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08, Reference De Stefani, Núñez-Betancourt and PérezDSNBP16] Suppose that
![]() $(R,\mathfrak{m},K)$
is a standard graded
$(R,\mathfrak{m},K)$
is a standard graded
![]() $K$
-algebra. If
$K$
-algebra. If
![]() $\unicode[STIX]{x1D708}_{I}(p^{e})=\max \{r\in \mathbb{N}\mid I^{r}\not \subseteq \mathfrak{m}^{[p^{e}]}\}$
, the
$\unicode[STIX]{x1D708}_{I}(p^{e})=\max \{r\in \mathbb{N}\mid I^{r}\not \subseteq \mathfrak{m}^{[p^{e}]}\}$
, the
![]() $F$
-threshold of
$F$
-threshold of
![]() $I$
with respect to
$I$
with respect to
![]() $\mathfrak{m}$
is defined by
$\mathfrak{m}$
is defined by
When
![]() $I=\mathfrak{m}$
, we call
$I=\mathfrak{m}$
, we call
![]() $c^{\mathfrak{m}}(\mathfrak{m})$
the diagonal
$c^{\mathfrak{m}}(\mathfrak{m})$
the diagonal
![]() $F$
-threshold of
$F$
-threshold of
![]() $R$
, and we denote it by
$R$
, and we denote it by
![]() $c^{\mathfrak{m}}(R)$
.
$c^{\mathfrak{m}}(R)$
.
![]() $F$
-thresholds were introduced for rings that are not necessarily regular by Huneke, Mustaţǎ, Takagi and Watanabe [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08]. However, the existence of the limit in complete generality has been shown only recently [Reference De Stefani, Núñez-Betancourt and PérezDSNBP16].
$F$
-thresholds were introduced for rings that are not necessarily regular by Huneke, Mustaţǎ, Takagi and Watanabe [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08]. However, the existence of the limit in complete generality has been shown only recently [Reference De Stefani, Núñez-Betancourt and PérezDSNBP16].
Definition 3.2. [Reference Takagi and WatanabeTW04] Let
![]() $(R,\mathfrak{m},K)$
be either a standard graded
$(R,\mathfrak{m},K)$
be either a standard graded
![]() $K$
-algebra or a local ring which is
$K$
-algebra or a local ring which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure, and let
$F$
-pure, and let
![]() $I\subseteq R$
be an ideal (homogeneous in the former case). For a real number
$I\subseteq R$
be an ideal (homogeneous in the former case). For a real number
![]() $\unicode[STIX]{x1D706}\geqslant 0$
, we say that
$\unicode[STIX]{x1D706}\geqslant 0$
, we say that
![]() $(R,I^{\unicode[STIX]{x1D706}})$
is
$(R,I^{\unicode[STIX]{x1D706}})$
is
![]() $F$
-pure if for every
$F$
-pure if for every
![]() $e\gg 0$
, there exists an element
$e\gg 0$
, there exists an element
![]() $f\in I^{\lfloor (p^{e}-1)\unicode[STIX]{x1D706}\rfloor }$
such that the inclusion of
$f\in I^{\lfloor (p^{e}-1)\unicode[STIX]{x1D706}\rfloor }$
such that the inclusion of
![]() $R$
-modules
$R$
-modules
![]() $f^{1/p^{e}}R\subseteq R^{1/p^{e}}$
splits.
$f^{1/p^{e}}R\subseteq R^{1/p^{e}}$
splits.
Remark 3.3. Note that
![]() $(R,I^{0})=(R,R)$
being
$(R,I^{0})=(R,R)$
being
![]() $F$
-pure simply means that
$F$
-pure simply means that
![]() $R$
is
$R$
is
![]() $F$
-pure, according to Definition 2.4.
$F$
-pure, according to Definition 2.4.
Definition 3.4. [Reference Takagi and WatanabeTW04] Let
![]() $(R,\mathfrak{m},K)$
be either a standard graded
$(R,\mathfrak{m},K)$
be either a standard graded
![]() $K$
-algebra or a local ring which is
$K$
-algebra or a local ring which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure, and let
$F$
-pure, and let
![]() $I\subseteq R$
be an ideal (homogeneous in the former case). The
$I\subseteq R$
be an ideal (homogeneous in the former case). The
![]() $F$
-pure threshold of
$F$
-pure threshold of
![]() $I$
is defined by
$I$
is defined by
When
![]() $I=\mathfrak{m}$
, we denote the
$I=\mathfrak{m}$
, we denote the
![]() $F$
-pure threshold by
$F$
-pure threshold by
![]() $\operatorname{fpt}(R)$
.
$\operatorname{fpt}(R)$
.
Definition 3.5. [Reference Aberbach and EnescuAE05] Let
![]() $(R,\mathfrak{m},K)$
be either a standard graded
$(R,\mathfrak{m},K)$
be either a standard graded
![]() $K$
-algebra or a local ring which is
$K$
-algebra or a local ring which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure. We define
$F$
-pure. We define
In addition, we define the splitting prime of
![]() $R$
as
$R$
as
![]() ${\mathcal{P}}(R):=\bigcap _{e}I_{e}(R)$
and the splitting dimension of
${\mathcal{P}}(R):=\bigcap _{e}I_{e}(R)$
and the splitting dimension of
![]() $R$
to be
$R$
to be
![]() $\operatorname{sdim}(R):=\dim (R/{\mathcal{P}}(R))$
.
$\operatorname{sdim}(R):=\dim (R/{\mathcal{P}}(R))$
.
Remark 3.6. We note that for a homogeneous element
![]() $r$
,
$r$
,
![]() $r\not \in I_{e}(R)$
if and only if there is a map
$r\not \in I_{e}(R)$
if and only if there is a map
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
such that
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
such that
![]() $\unicode[STIX]{x1D711}(r^{1/p^{e}})=1$
.
$\unicode[STIX]{x1D711}(r^{1/p^{e}})=1$
.
The following proposition gives basic properties of the splitting prime for graded algebras. We include details of the proof in the graded case for sake of completeness.
Proposition 3.7. [Reference Aberbach and EnescuAE05]
Let
![]() $(R,\mathfrak{m},K)$
be an
$(R,\mathfrak{m},K)$
be an
![]() $F$
-finite
$F$
-finite
![]() $F$
-pure standard graded
$F$
-pure standard graded
![]() $K$
-algebra. Then
$K$
-algebra. Then
-
(1)
 $I_{e}(R)$
and
$I_{e}(R)$
and
 ${\mathcal{P}}(R)$
are homogeneous ideals.
${\mathcal{P}}(R)$
are homogeneous ideals. -
(2)
 ${\mathcal{P}}(R)$
is a prime ideal.
${\mathcal{P}}(R)$
is a prime ideal. -
(3)
 ${\mathcal{P}}(R)$
is the largest homogeneous compatible ideal of
${\mathcal{P}}(R)$
is the largest homogeneous compatible ideal of
 $R$
, that is, the largest homogeneous ideal that is
$R$
, that is, the largest homogeneous ideal that is
 $\unicode[STIX]{x1D711}$
-compatible for all
$\unicode[STIX]{x1D711}$
-compatible for all
 $\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
, and all
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
, and all
 $e\in \mathbb{N}$
.
$e\in \mathbb{N}$
. -
(4)
 $R/{\mathcal{P}}(R)$
is strongly
$R/{\mathcal{P}}(R)$
is strongly
 $F$
-regular.
$F$
-regular. -
(5)
 ${\mathcal{P}}(R)_{\mathfrak{m}}={\mathcal{P}}(R_{\mathfrak{m}})$
.
${\mathcal{P}}(R)_{\mathfrak{m}}={\mathcal{P}}(R_{\mathfrak{m}})$
.
Proof.
(1) Let
![]() $e\geqslant 1$
. Since both
$e\geqslant 1$
. Since both
![]() $R^{1/p^{e}}$
and
$R^{1/p^{e}}$
and
![]() $R$
are graded, and
$R$
are graded, and
![]() $R^{1/p^{e}}$
is a finitely generated
$R^{1/p^{e}}$
is a finitely generated
![]() $R$
-module, we have that every homomorphism
$R$
-module, we have that every homomorphism
![]() $R^{1/p^{e}}\rightarrow R$
is a sum of graded homomorphisms. Therefore, in the definition of
$R^{1/p^{e}}\rightarrow R$
is a sum of graded homomorphisms. Therefore, in the definition of
![]() $I_{e}(R)$
above, we can consider only graded homomorphisms. Let
$I_{e}(R)$
above, we can consider only graded homomorphisms. Let
![]() $r=r_{0}+r_{1}+\cdots +r_{n}\in I_{e}(R)$
, with
$r=r_{0}+r_{1}+\cdots +r_{n}\in I_{e}(R)$
, with
![]() $r_{i}$
of degree
$r_{i}$
of degree
![]() $d_{i}$
. Let
$d_{i}$
. Let
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
be homogeneous of degree
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
be homogeneous of degree
![]() $k$
. Then
$k$
. Then
and each
![]() $\unicode[STIX]{x1D711}(r_{i}^{1/p^{e}})$
now has degree
$\unicode[STIX]{x1D711}(r_{i}^{1/p^{e}})$
now has degree
![]() $d_{i}+k$
. Since
$d_{i}+k$
. Since
![]() $\mathfrak{m}$
is homogeneous, we get
$\mathfrak{m}$
is homogeneous, we get
![]() $\unicode[STIX]{x1D711}(r_{i}^{1/p^{e}})\in \mathfrak{m}$
for all
$\unicode[STIX]{x1D711}(r_{i}^{1/p^{e}})\in \mathfrak{m}$
for all
![]() $i=1,\ldots ,n$
, showing that
$i=1,\ldots ,n$
, showing that
![]() $r_{i}\in I_{e}(R)$
. Then
$r_{i}\in I_{e}(R)$
. Then
![]() $I_{e}(R)$
is a homogeneous ideal. We have that
$I_{e}(R)$
is a homogeneous ideal. We have that
![]() ${\mathcal{P}}(R)$
is homogeneous is clear from its definition. The proofs of (2), (3) and (4) are completely analogous to the ones in [Reference Aberbach and EnescuAE05, Theorems 3.3, and 4.7] and [Reference SchwedeSch10, Remark 4.4] for local rings. For (5), we note that
${\mathcal{P}}(R)$
is homogeneous is clear from its definition. The proofs of (2), (3) and (4) are completely analogous to the ones in [Reference Aberbach and EnescuAE05, Theorems 3.3, and 4.7] and [Reference SchwedeSch10, Remark 4.4] for local rings. For (5), we note that
![]() $\unicode[STIX]{x1D711}({\mathcal{P}}(R)_{\mathfrak{m}}^{1/p^{e}})\subseteq {\mathcal{P}}(R)_{\mathfrak{m}}$
for every
$\unicode[STIX]{x1D711}({\mathcal{P}}(R)_{\mathfrak{m}}^{1/p^{e}})\subseteq {\mathcal{P}}(R)_{\mathfrak{m}}$
for every
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(R_{\mathfrak{m}}^{1/p^{e}},R_{\mathfrak{m}})$
because
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(R_{\mathfrak{m}}^{1/p^{e}},R_{\mathfrak{m}})$
because
![]() $R$
is
$R$
is
![]() $F$
-finite. Since
$F$
-finite. Since
![]() $R_{\mathfrak{m}}/({\mathcal{P}}(R)_{\mathfrak{m}})$
is strongly
$R_{\mathfrak{m}}/({\mathcal{P}}(R)_{\mathfrak{m}})$
is strongly
![]() $F$
-regular by (4), we have that
$F$
-regular by (4), we have that
![]() ${\mathcal{P}}(R)_{\mathfrak{m}}={\mathcal{P}}(R_{\mathfrak{m}}).$
◻
${\mathcal{P}}(R)_{\mathfrak{m}}={\mathcal{P}}(R_{\mathfrak{m}}).$
◻
Definition 3.8. Let
![]() $(R,\mathfrak{m},K)$
be an
$(R,\mathfrak{m},K)$
be an
![]() $F$
-finite
$F$
-finite
![]() $F$
-pure standard graded
$F$
-pure standard graded
![]() $K$
-algebra. Let
$K$
-algebra. Let
![]() $J\subseteq R$
be a homogeneous ideal. Then, we define
$J\subseteq R$
be a homogeneous ideal. Then, we define
Lemma 3.9. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure. Let
$F$
-pure. Let
![]() $J\subseteq R$
be a homogeneous ideal. Then,
$J\subseteq R$
be a homogeneous ideal. Then,
![]() $p\cdot b_{J}(p^{e})\leqslant b_{J}(p^{e+1})$
.
$p\cdot b_{J}(p^{e})\leqslant b_{J}(p^{e+1})$
.
Proof. Let
![]() $f\in J^{b_{J}(p^{e})}\smallsetminus I_{e}(R)$
be a homogeneous element. Then,
$f\in J^{b_{J}(p^{e})}\smallsetminus I_{e}(R)$
be a homogeneous element. Then,
![]() $Rf^{1/p^{e}}\rightarrow R^{1/p^{e}}$
splits as map of
$Rf^{1/p^{e}}\rightarrow R^{1/p^{e}}$
splits as map of
![]() $R$
-modules. Since
$R$
-modules. Since
![]() $R$
is
$R$
is
![]() $F$
-pure, there is a splitting
$F$
-pure, there is a splitting
![]() $\unicode[STIX]{x1D6FC}:R^{1/p^{e+1}}\rightarrow R^{1/p^{e}}$
as
$\unicode[STIX]{x1D6FC}:R^{1/p^{e+1}}\rightarrow R^{1/p^{e}}$
as
![]() $R^{1/p^{e}}$
-modules. Then,
$R^{1/p^{e}}$
-modules. Then,
splits as morphism of
![]() $R$
-modules. Therefore,
$R$
-modules. Therefore,
![]() $Rf^{p/p^{e+1}}\rightarrow R^{1/p^{e+1}}$
splits as a map of
$Rf^{p/p^{e+1}}\rightarrow R^{1/p^{e+1}}$
splits as a map of
![]() $R$
-modules. Hence,
$R$
-modules. Hence,
![]() $f^{p}\in J^{p\cdot b_{J}(p^{e})}\smallsetminus I_{e+1}(R)$
, and so,
$f^{p}\in J^{p\cdot b_{J}(p^{e})}\smallsetminus I_{e+1}(R)$
, and so,
![]() $p\cdot b_{J}(p^{e})\leqslant b_{J}(p^{e+1})$
.◻
$p\cdot b_{J}(p^{e})\leqslant b_{J}(p^{e+1})$
.◻
We now present a characterization of the
![]() $F$
-pure threshold that may be known to experts (see [Reference HernándezHer12, Key lemma] for principal ideals). However, we were not able to find it in the literature in the generality we need. We present the proof for the sake of completeness. This characterization is a key part for the proof of Theorem 4.3.
$F$
-pure threshold that may be known to experts (see [Reference HernándezHer12, Key lemma] for principal ideals). However, we were not able to find it in the literature in the generality we need. We present the proof for the sake of completeness. This characterization is a key part for the proof of Theorem 4.3.
Proposition 3.10. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure. Let
$F$
-pure. Let
![]() $J\subseteq R$
be a homogeneous ideal. Then
$J\subseteq R$
be a homogeneous ideal. Then
Proof. By the definition of
![]() $b_{J}(p^{e}),$
there exists
$b_{J}(p^{e}),$
there exists
![]() $f\in J^{b_{J}(p^{e})}\setminus I_{e}(R).$
Then, the map
$f\in J^{b_{J}(p^{e})}\setminus I_{e}(R).$
Then, the map
![]() $R\rightarrow R^{1/p^{e}}$
, defined by
$R\rightarrow R^{1/p^{e}}$
, defined by
![]() $1\mapsto f^{1/p^{e}}$
splits by Remark 3.6. Thus,
$1\mapsto f^{1/p^{e}}$
splits by Remark 3.6. Thus,
![]() $b_{J}(p^{e})/p^{e}\in \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid (R,J^{\unicode[STIX]{x1D706}})\text{ is }F\text{-pure}\}$
. Hence, for all
$b_{J}(p^{e})/p^{e}\in \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid (R,J^{\unicode[STIX]{x1D706}})\text{ is }F\text{-pure}\}$
. Hence, for all
![]() $e$
, we have
$e$
, we have
![]() $b_{J}(p^{e})/p^{e}\leqslant \operatorname{fpt}(J)$
, and therefore
$b_{J}(p^{e})/p^{e}\leqslant \operatorname{fpt}(J)$
, and therefore
![]() $\{b_{J}(p^{e})/p^{e}\}$
is a bounded sequence. By Lemma 3.9 we conclude that
$\{b_{J}(p^{e})/p^{e}\}$
is a bounded sequence. By Lemma 3.9 we conclude that
![]() $\lim _{e\rightarrow \infty }b_{J}(p^{e})/p^{e}$
exists, and that
$\lim _{e\rightarrow \infty }b_{J}(p^{e})/p^{e}$
exists, and that
![]() $\lim _{e\rightarrow \infty }b_{J}(p^{e})/p^{e}\leqslant \operatorname{fpt}(J)$
.
$\lim _{e\rightarrow \infty }b_{J}(p^{e})/p^{e}\leqslant \operatorname{fpt}(J)$
.
Conversely, let
![]() $\unicode[STIX]{x1D70E}\in \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid (R,J^{\unicode[STIX]{x1D706}})\text{ is }F\text{-pure}\}$
. For
$\unicode[STIX]{x1D70E}\in \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid (R,J^{\unicode[STIX]{x1D706}})\text{ is }F\text{-pure}\}$
. For
![]() $e\gg 0$
, we have that
$e\gg 0$
, we have that
![]() $J^{\lfloor (p^{e}-1)\unicode[STIX]{x1D70E}\rfloor }\not \subseteq I_{e}(R)$
. Then,
$J^{\lfloor (p^{e}-1)\unicode[STIX]{x1D70E}\rfloor }\not \subseteq I_{e}(R)$
. Then,
![]() $\lfloor (p^{e}-1)\unicode[STIX]{x1D70E}\rfloor /p^{e}\leqslant b_{J}(p^{e})/p^{e}$
and thus
$\lfloor (p^{e}-1)\unicode[STIX]{x1D70E}\rfloor /p^{e}\leqslant b_{J}(p^{e})/p^{e}$
and thus
Hence,
Remark 3.11. We note that analogous restatements of Proposition 3.10 for
![]() $F$
-finite
$F$
-finite
![]() $F$
-pure local rings is also true, and the proof is essentially the same.
$F$
-pure local rings is also true, and the proof is essentially the same.
4 F-thresholds and
 $a$
-invariants
$a$
-invariants
In this section, we prove the first part of our main theorem in positive characteristic. We start with a few preparation lemmas.
Lemma 4.1. Let
![]() $(S,\mathfrak{n},K)$
be a standard graded
$(S,\mathfrak{n},K)$
be a standard graded
![]() $F$
-finite regular ring. Let
$F$
-finite regular ring. Let
![]() $I\subseteq S$
be an ideal such that
$I\subseteq S$
be an ideal such that
![]() $R=S/I$
is an
$R=S/I$
is an
![]() $F$
-pure ring. Let
$F$
-pure ring. Let
![]() $\mathfrak{m}=\mathfrak{n}R$
. Then,
$\mathfrak{m}=\mathfrak{n}R$
. Then,
![]() ${\mathcal{P}}(R)=\mathfrak{m}$
if and only if
${\mathcal{P}}(R)=\mathfrak{m}$
if and only if
![]() $(I^{[p^{e}]}:I)\subseteq (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
for all
$(I^{[p^{e}]}:I)\subseteq (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
for all
![]() $e\geqslant 0$
.
$e\geqslant 0$
.
Proof. Let
![]() $\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
denote the
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
denote the
![]() $e$
-trace map. If
$e$
-trace map. If
![]() $(I^{[p^{e}]}:I)\subseteq (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
, then for every
$(I^{[p^{e}]}:I)\subseteq (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
, then for every
![]() $f\in (I^{[p^{e}]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
there exist a unit
$f\in (I^{[p^{e}]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
there exist a unit
![]() $u\in S$
and an element
$u\in S$
and an element
![]() $g\in \mathfrak{n}^{[p^{e}]}$
such that
$g\in \mathfrak{n}^{[p^{e}]}$
such that
![]() $f=ux_{1}^{p^{e}-1}\cdots x_{n}^{p^{e}-1}+g.$
Then,
$f=ux_{1}^{p^{e}-1}\cdots x_{n}^{p^{e}-1}+g.$
Then,
![]() $f\cdot \mathfrak{n}\subseteq \mathfrak{n}^{[p^{e}]}$
, and we get
$f\cdot \mathfrak{n}\subseteq \mathfrak{n}^{[p^{e}]}$
, and we get
![]() $\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}\mathfrak{n}^{1/p^{e}})\subseteq \mathfrak{n}$
. Then by Remark 2.10, we have that
$\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}\mathfrak{n}^{1/p^{e}})\subseteq \mathfrak{n}$
. Then by Remark 2.10, we have that
![]() $\unicode[STIX]{x1D711}(\mathfrak{m}^{1/p^{e}})\subseteq \mathfrak{m}$
for every
$\unicode[STIX]{x1D711}(\mathfrak{m}^{1/p^{e}})\subseteq \mathfrak{m}$
for every
![]() $\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R.$
Hence,
$\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R.$
Hence,
![]() $I_{e}(R)=\mathfrak{m}$
for all
$I_{e}(R)=\mathfrak{m}$
for all
![]() $e\geqslant 1$
and
$e\geqslant 1$
and
![]() ${\mathcal{P}}(R)=\mathfrak{m}$
as well.
${\mathcal{P}}(R)=\mathfrak{m}$
as well.
Conversely, if
![]() $\mathfrak{m}={\mathcal{P}}(R)$
, then
$\mathfrak{m}={\mathcal{P}}(R)$
, then
![]() $I_{e}(R)=\mathfrak{m}$
for all
$I_{e}(R)=\mathfrak{m}$
for all
![]() $e\geqslant 1$
. This means that for every
$e\geqslant 1$
. This means that for every
![]() $e\geqslant 1$
and every
$e\geqslant 1$
and every
![]() $f\in (I^{[p^{e}]}:I)$
, we have
$f\in (I^{[p^{e}]}:I)$
, we have
![]() $\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}\mathfrak{n}^{1/p^{e}})\subseteq \mathfrak{n}$
by Remark 2.10. Thus,
$\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}\mathfrak{n}^{1/p^{e}})\subseteq \mathfrak{n}$
by Remark 2.10. Thus,
![]() $f\cdot \mathfrak{n}\subseteq \mathfrak{n}^{[p^{e}]},$
and hence
$f\cdot \mathfrak{n}\subseteq \mathfrak{n}^{[p^{e}]},$
and hence
![]() $f\in (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
.◻
$f\in (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
.◻
Lemma 4.2. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
![]() $F$
-finite field
$F$
-finite field
![]() $K$
. Let
$K$
. Let
![]() $\mathfrak{n}=(x_{1},\ldots ,x_{n})$
denote the maximal homogeneous ideal. Let
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
denote the maximal homogeneous ideal. Let
![]() $I\subseteq S$
be a homogeneous ideal such that
$I\subseteq S$
be a homogeneous ideal such that
![]() $R:=S/I$
is an
$R:=S/I$
is an
![]() $F$
-pure ring, and let
$F$
-pure ring, and let
![]() $\mathfrak{m}=\mathfrak{n}R$
. Then,
$\mathfrak{m}=\mathfrak{n}R$
. Then,
Proof. Let
![]() $\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
denote the
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
denote the
![]() $e$
-trace map. Let
$e$
-trace map. Let
and
![]() $b=b_{\mathfrak{m}}(p^{e})$
. By our definition of
$b=b_{\mathfrak{m}}(p^{e})$
. By our definition of
![]() $u$
, there exists
$u$
, there exists
![]() $f\in (I^{[p^{e}]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
, which is a homogeneous polynomial of degree
$f\in (I^{[p^{e}]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
, which is a homogeneous polynomial of degree
![]() $u$
. Since
$u$
. Since
![]() $f\not \in \mathfrak{n}^{[p^{e}]},$
there exists
$f\not \in \mathfrak{n}^{[p^{e}]},$
there exists
![]() $x^{\unicode[STIX]{x1D6FC}}\in \operatorname{Supp}\{f\}$
such that
$x^{\unicode[STIX]{x1D6FC}}\in \operatorname{Supp}\{f\}$
such that
![]() $x^{\unicode[STIX]{x1D6FC}}\not \in \mathfrak{n}^{[p^{e}]}$
. We pick
$x^{\unicode[STIX]{x1D6FC}}\not \in \mathfrak{n}^{[p^{e}]}$
. We pick
![]() $\unicode[STIX]{x1D6FD}=\mathbf{p}^{\mathbf{e}}-\mathbf{1}-\unicode[STIX]{x1D6FC}$
, so
$\unicode[STIX]{x1D6FD}=\mathbf{p}^{\mathbf{e}}-\mathbf{1}-\unicode[STIX]{x1D6FC}$
, so
![]() $x^{\unicode[STIX]{x1D6FC}}x^{\unicode[STIX]{x1D6FD}}=x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}$
, where
$x^{\unicode[STIX]{x1D6FC}}x^{\unicode[STIX]{x1D6FD}}=x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}$
, where
![]() $\mathbf{p}^{\mathbf{e}}-\mathbf{1}$
denotes the multi-index
$\mathbf{p}^{\mathbf{e}}-\mathbf{1}$
denotes the multi-index
![]() $(p^{e}-1,p^{e}-1,\ldots ,p^{e}-1)$
. We have that the map
$(p^{e}-1,p^{e}-1,\ldots ,p^{e}-1)$
. We have that the map
![]() $\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R$
defined by
$\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R$
defined by
![]() $\unicode[STIX]{x1D711}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r^{1/p^{e}})}$
is a splitting of the Frobenius map on
$\unicode[STIX]{x1D711}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r^{1/p^{e}})}$
is a splitting of the Frobenius map on
![]() $R$
such that
$R$
such that
![]() $\unicode[STIX]{x1D711}((x^{\unicode[STIX]{x1D6FD}})^{1/p^{e}})=1$
. Hence,
$\unicode[STIX]{x1D711}((x^{\unicode[STIX]{x1D6FD}})^{1/p^{e}})=1$
. Hence,
![]() $x^{\unicode[STIX]{x1D6FD}}\notin I_{e}(R)$
. Since
$x^{\unicode[STIX]{x1D6FD}}\notin I_{e}(R)$
. Since
![]() $|\unicode[STIX]{x1D6FD}|=(p^{e}-1)n-u,$
we have that
$|\unicode[STIX]{x1D6FD}|=(p^{e}-1)n-u,$
we have that
![]() $(p^{e}-1)n-u\leqslant b$
; that is,
$(p^{e}-1)n-u\leqslant b$
; that is,
![]() $u\geqslant n(p^{e}-1)-b$
.
$u\geqslant n(p^{e}-1)-b$
.
For the other inequality, we pick a monomial
![]() $g\in \mathfrak{n}$
of degree
$g\in \mathfrak{n}$
of degree
![]() $b$
such that
$b$
such that
![]() $\overline{g}\in \mathfrak{m}^{b}\smallsetminus I_{e}(R)$
. Then, there exists a map
$\overline{g}\in \mathfrak{m}^{b}\smallsetminus I_{e}(R)$
. Then, there exists a map
![]() $\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R$
such that
$\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R$
such that
![]() $\unicode[STIX]{x1D711}(\overline{g}^{1/p^{e}})=1.$
Therefore, there exists an element
$\unicode[STIX]{x1D711}(\overline{g}^{1/p^{e}})=1.$
Therefore, there exists an element
![]() $f\in (I^{[q]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
such that
$f\in (I^{[q]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
such that
![]() $\unicode[STIX]{x1D711}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r^{1/p^{e}})}$
for all
$\unicode[STIX]{x1D711}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r^{1/p^{e}})}$
for all
![]() $\overline{r}^{1/p^{e}}\in R^{1/p^{e}}$
. By definition of
$\overline{r}^{1/p^{e}}\in R^{1/p^{e}}$
. By definition of
![]() $\unicode[STIX]{x1D6F7}_{e},$
we have that
$\unicode[STIX]{x1D6F7}_{e},$
we have that
![]() $x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}\in \operatorname{Supp}(fg)$
. Let
$x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}\in \operatorname{Supp}(fg)$
. Let
![]() $h$
be the homogeneous part of degree
$h$
be the homogeneous part of degree
![]() $(p-1)n-b$
of
$(p-1)n-b$
of
![]() $f$
. We note that
$f$
. We note that
![]() $h\in (I^{[p^{e}]}:I)$
because
$h\in (I^{[p^{e}]}:I)$
because
![]() $I$
is homogeneous. In addition,
$I$
is homogeneous. In addition,
![]() $h\notin \mathfrak{n}^{[p^{e}]}$
because
$h\notin \mathfrak{n}^{[p^{e}]}$
because
![]() $x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}\in \operatorname{Supp}(hg)$
. Then we get
$x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}\in \operatorname{Supp}(hg)$
. Then we get
![]() $u\leqslant (p^{e}-1)n-b$
, as desired.◻
$u\leqslant (p^{e}-1)n-b$
, as desired.◻
We are now ready to prove the first part of Theorem B.
Theorem 4.3. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure. Then
$F$
-pure. Then
![]() $\operatorname{fpt}(R)\leqslant -a_{i}(R)$
for every
$\operatorname{fpt}(R)\leqslant -a_{i}(R)$
for every
![]() $i\in \mathbb{N}$
.
$i\in \mathbb{N}$
.
Proof. If
![]() $H_{\mathfrak{m}}^{i}(R)=0$
there is nothing to prove, since
$H_{\mathfrak{m}}^{i}(R)=0$
there is nothing to prove, since
![]() $a_{i}(R)=-\infty$
. Let
$a_{i}(R)=-\infty$
. Let
![]() $i\in \mathbb{N}$
be such that
$i\in \mathbb{N}$
be such that
![]() $H_{\mathfrak{m}}^{i}(R)\neq 0$
. Let
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. Let
![]() $f\in \mathfrak{m}^{b_{\mathfrak{m}}(p^{e})}\setminus I_{e}(R)$
be a homogeneous element, and let
$f\in \mathfrak{m}^{b_{\mathfrak{m}}(p^{e})}\setminus I_{e}(R)$
be a homogeneous element, and let
![]() $\unicode[STIX]{x1D6FE}=b_{\mathfrak{m}}(p^{e})/p^{e}$
. By Remark 2.1 we can view
$\unicode[STIX]{x1D6FE}=b_{\mathfrak{m}}(p^{e})/p^{e}$
. By Remark 2.1 we can view
![]() $R$
as a
$R$
as a
![]() $1/p^{e}\mathbb{N}$
-graded module. Then
$1/p^{e}\mathbb{N}$
-graded module. Then
![]()
splits, and the inclusion is homogeneous of degree zero. Applying the
![]() $i$
th local cohomology, we get a homogeneous split inclusion
$i$
th local cohomology, we get a homogeneous split inclusion
![]() $H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE})){\hookrightarrow}H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
of degree zero. Let
$H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE})){\hookrightarrow}H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
of degree zero. Let
![]() $v\in H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE}))_{a_{i}(R)}$
be an element in the top graded part of
$v\in H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE}))_{a_{i}(R)}$
be an element in the top graded part of
![]() $H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE}))$
, which has degree
$H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE}))$
, which has degree
![]() $a_{i}(R)+\unicode[STIX]{x1D6FE}$
. Under the inclusion above, this maps to a nonzero element of degree
$a_{i}(R)+\unicode[STIX]{x1D6FE}$
. Under the inclusion above, this maps to a nonzero element of degree
![]() $a_{i}(R)+\unicode[STIX]{x1D6FE}$
in
$a_{i}(R)+\unicode[STIX]{x1D6FE}$
in
![]() $H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
. Therefore,
$H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
. Therefore,
which is equivalent to
Since this holds for all
![]() $e\gg 1$
, we get
$e\gg 1$
, we get
by Proposition 3.10. ◻
Corollary 4.4. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure. If
$F$
-pure. If
![]() $a_{i}(R)=0$
for some
$a_{i}(R)=0$
for some
![]() $i$
, then
$i$
, then
![]() $\operatorname{sdim}(R)=0$
.
$\operatorname{sdim}(R)=0$
.
Proof. If
![]() $a_{i}(R)=0$
for some
$a_{i}(R)=0$
for some
![]() $i$
, we have that
$i$
, we have that
![]() $\operatorname{fpt}(R)=0$
by Theorem 4.3. Then, we have that
$\operatorname{fpt}(R)=0$
by Theorem 4.3. Then, we have that
![]() $b_{e}=0$
for every
$b_{e}=0$
for every
![]() $e\in \mathbb{N}$
by Lemma 3.9 and Proposition 3.10. As a consequence,
$e\in \mathbb{N}$
by Lemma 3.9 and Proposition 3.10. As a consequence,
![]() $\mathfrak{m}\subseteq I_{e}$
for every
$\mathfrak{m}\subseteq I_{e}$
for every
![]() $e\in \mathbb{N}.$
Since
$e\in \mathbb{N}.$
Since
![]() $I_{e}(R)\subseteq \mathfrak{m}$
holds true because
$I_{e}(R)\subseteq \mathfrak{m}$
holds true because
![]() $R$
is
$R$
is
![]() $F$
-pure, we have that
$F$
-pure, we have that
![]() $\mathfrak{m}=I_{e}(R)$
for every
$\mathfrak{m}=I_{e}(R)$
for every
![]() $e\in \mathbb{N}.$
Hence,
$e\in \mathbb{N}.$
Hence,
![]() ${\mathcal{P}}(R)=\mathfrak{m},$
and
${\mathcal{P}}(R)=\mathfrak{m},$
and
![]() $\operatorname{sdim}(R)=0.$
◻
$\operatorname{sdim}(R)=0.$
◻
We now review the definition of test ideal, which is closely related to the theory of tight closure. We refer the reader to [Reference Hochster and HunekeHH94] for definitions and details.
Definition 4.5. Let
![]() $R$
be a Noetherian ring of positive characteristic
$R$
be a Noetherian ring of positive characteristic
![]() $p$
. The finitistic test ideal of
$p$
. The finitistic test ideal of
![]() $R$
is defined as
$R$
is defined as
![]() $\unicode[STIX]{x1D70F}^{fg}(R):=\cap _{M}\operatorname{ann}(0_{M}^{\ast })$
, where
$\unicode[STIX]{x1D70F}^{fg}(R):=\cap _{M}\operatorname{ann}(0_{M}^{\ast })$
, where
![]() $M$
runs through all the finitely generated
$M$
runs through all the finitely generated
![]() $R$
-modules. We define the big test ideal of
$R$
-modules. We define the big test ideal of
![]() $R$
to be
$R$
to be
![]() $\unicode[STIX]{x1D70F}(R)=\cap _{M}\operatorname{ann}(0_{M}^{\ast })$
, where
$\unicode[STIX]{x1D70F}(R)=\cap _{M}\operatorname{ann}(0_{M}^{\ast })$
, where
![]() $M$
runs through all
$M$
runs through all
![]() $R$
-modules.
$R$
-modules.
Remark 4.6. We point out that for
![]() $F$
-finite rings,
$F$
-finite rings,
![]() $\unicode[STIX]{x1D70F}(R)$
is the smallest compatible ideal not contained in a minimal prime of
$\unicode[STIX]{x1D70F}(R)$
is the smallest compatible ideal not contained in a minimal prime of
![]() $R$
[Reference SchwedeSch10, Theorem 6.3]. In addition,
$R$
[Reference SchwedeSch10, Theorem 6.3]. In addition,
![]() $\unicode[STIX]{x1D70F}^{fg}(R)$
is a compatible ideal [Reference VassilevVas98, Theorem 3.1]. One clearly has the inclusion
$\unicode[STIX]{x1D70F}^{fg}(R)$
is a compatible ideal [Reference VassilevVas98, Theorem 3.1]. One clearly has the inclusion
![]() $\unicode[STIX]{x1D70F}(R)\subseteq \unicode[STIX]{x1D70F}^{fg}(R)$
. It is one of the most important open problems in tight closure theory whether these two ideals are the same. Equality is known to hold true in some cases. For instance, Lyubeznik and Smith proved that
$\unicode[STIX]{x1D70F}(R)\subseteq \unicode[STIX]{x1D70F}^{fg}(R)$
. It is one of the most important open problems in tight closure theory whether these two ideals are the same. Equality is known to hold true in some cases. For instance, Lyubeznik and Smith proved that
![]() $\unicode[STIX]{x1D70F}^{fg}(R)=\unicode[STIX]{x1D70F}(R)$
for finitely generated standard graded
$\unicode[STIX]{x1D70F}^{fg}(R)=\unicode[STIX]{x1D70F}(R)$
for finitely generated standard graded
![]() $K$
-algebras [Reference Lyubeznik and SmithLS99, Corollary 3.4].
$K$
-algebras [Reference Lyubeznik and SmithLS99, Corollary 3.4].
We use Proposition 3.10 to relate the
![]() $F$
-pure threshold of the ring with its splitting dimension.
$F$
-pure threshold of the ring with its splitting dimension.
Theorem 4.7. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure, and let
$F$
-pure, and let
![]() $J\subseteq R$
be a compatible ideal. Then, we have
$J\subseteq R$
be a compatible ideal. Then, we have
In particular,
where
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}(R)$
denotes the test ideal of
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}(R)$
denotes the test ideal of
![]() $R$
, and
$R$
, and
![]() ${\mathcal{P}}={\mathcal{P}}(R)$
is the splitting prime of
${\mathcal{P}}={\mathcal{P}}(R)$
is the splitting prime of
![]() $R$
.
$R$
.
Proof. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring such that there exists a surjection
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring such that there exists a surjection
![]() $S\rightarrow R$
, and let
$S\rightarrow R$
, and let
![]() $\mathfrak{n}=(x_{1},\ldots ,x_{n})$
, so that
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
, so that
![]() $\mathfrak{m}=\mathfrak{n}R$
. Let
$\mathfrak{m}=\mathfrak{n}R$
. Let
![]() $I$
denote the kernel of the surjection. Let
$I$
denote the kernel of the surjection. Let
![]() $\widetilde{J}\subseteq S$
be the pullback of
$\widetilde{J}\subseteq S$
be the pullback of
![]() $J$
. We have that
$J$
. We have that
![]() $(I^{[p^{e}]}:I)\subseteq (\widetilde{J}^{[p^{e}]}:\widetilde{J})$
for every
$(I^{[p^{e}]}:I)\subseteq (\widetilde{J}^{[p^{e}]}:\widetilde{J})$
for every
![]() $e\in \mathbb{N}$
by Remark 2.11. Then,
$e\in \mathbb{N}$
by Remark 2.11. Then,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \min \left\{t\in \mathbb{N}~\bigg|\left[\frac{(\widetilde{J}^{[p^{e}]}:\widetilde{J})+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{t}\neq 0\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \min \left\{t\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{t}\neq 0\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \min \left\{t\in \mathbb{N}~\bigg|\left[\frac{(\widetilde{J}^{[p^{e}]}:\widetilde{J})+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{t}\neq 0\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \min \left\{t\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{t}\neq 0\right\}.\nonumber\end{eqnarray}$$
As a consequence, we get
by Proposition 3.10. Then,
![]() $\operatorname{fpt}(R)\leqslant \operatorname{fpt}(R/J)$
. The last claim follows from the fact that the test ideal is compatible as noted in Remark 4.6, and the splitting prime is compatible by Proposition 3.7
(3). Finally,
$\operatorname{fpt}(R)\leqslant \operatorname{fpt}(R/J)$
. The last claim follows from the fact that the test ideal is compatible as noted in Remark 4.6, and the splitting prime is compatible by Proposition 3.7
(3). Finally,
![]() $\operatorname{fpt}(R/{\mathcal{P}})\leqslant \dim (R/{\mathcal{P}})$
[Reference Takagi and WatanabeTW04, Proposition 2.6(1)].◻
$\operatorname{fpt}(R/{\mathcal{P}})\leqslant \dim (R/{\mathcal{P}})$
[Reference Takagi and WatanabeTW04, Proposition 2.6(1)].◻
We now focus on the diagonal
![]() $F$
-threshold.
$F$
-threshold.
Remark 4.8. For any standard graded
![]() $K$
-algebra
$K$
-algebra
![]() $(R,\mathfrak{m},K)$
, we have that
$(R,\mathfrak{m},K)$
, we have that
We are now ready to prove the second part of Theorem B.
Theorem 4.9. Let
![]() $R$
be an
$R$
be an
![]() $F$
-finite standard graded
$F$
-finite standard graded
![]() $K$
-algebra, and let
$K$
-algebra, and let
![]() $d=\dim (R)$
. Then,
$d=\dim (R)$
. Then,
![]() $-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
. Furthermore, if
$-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
. Furthermore, if
![]() $R$
is
$R$
is
![]() $F$
-pure, then
$F$
-pure, then
![]() $-a_{i}(R)\leqslant c^{\mathfrak{m}}(R)$
for every
$-a_{i}(R)\leqslant c^{\mathfrak{m}}(R)$
for every
![]() $i$
such that
$i$
such that
![]() $H_{\mathfrak{m}}^{i}(R)\neq 0$
.
$H_{\mathfrak{m}}^{i}(R)\neq 0$
.
Proof. We fix
![]() $i\in \mathbb{N}$
such that
$i\in \mathbb{N}$
such that
![]() $H_{\mathfrak{m}}^{i}(R)\neq 0$
. Let
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. Let
![]() $v_{1},\ldots ,v_{r}$
be a minimal system of homogeneous generators of
$v_{1},\ldots ,v_{r}$
be a minimal system of homogeneous generators of
![]() $R^{1/p^{e}}$
as an
$R^{1/p^{e}}$
as an
![]() $R$
-module, with degrees
$R$
-module, with degrees
![]() $\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{r}\in 1/p^{e}\mathbb{N}$
. By Remark 2.1 we can view
$\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{r}\in 1/p^{e}\mathbb{N}$
. By Remark 2.1 we can view
![]() $R$
as a
$R$
as a
![]() $1/p^{e}\mathbb{N}$
-graded module. We have a degree zero surjective map
$1/p^{e}\mathbb{N}$
-graded module. We have a degree zero surjective map
where
![]() $R(-\unicode[STIX]{x1D6FE}_{j})\rightarrow R^{1/p^{e}}$
maps
$R(-\unicode[STIX]{x1D6FE}_{j})\rightarrow R^{1/p^{e}}$
maps
![]() $1$
to
$1$
to
![]() $v_{j}.$
This induces a degree zero homomorphism
$v_{j}.$
This induces a degree zero homomorphism
If
![]() $i=d,$
$i=d,$
![]() $\unicode[STIX]{x1D711}$
is surjective. We now prove that
$\unicode[STIX]{x1D711}$
is surjective. We now prove that
![]() $\unicode[STIX]{x1D711}$
is also surjective for
$\unicode[STIX]{x1D711}$
is also surjective for
![]() $i\neq d$
, if
$i\neq d$
, if
![]() $R$
is
$R$
is
![]() $F$
-pure. In this case, the natural inclusion
$F$
-pure. In this case, the natural inclusion
![]() $R\rightarrow R^{1/p^{e}}$
induces an inclusion
$R\rightarrow R^{1/p^{e}}$
induces an inclusion
![]() $H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
. We have that the map
$H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
. We have that the map
![]() $\unicode[STIX]{x1D703}:H_{\mathfrak{m}}^{i}(R)\otimes _{R}R^{1/p^{e}}\rightarrow H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
induced by
$\unicode[STIX]{x1D703}:H_{\mathfrak{m}}^{i}(R)\otimes _{R}R^{1/p^{e}}\rightarrow H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
induced by
![]() $v\otimes f^{1/p^{e}}\mapsto f^{1/p^{e}}\unicode[STIX]{x1D6FC}(v)$
is surjective [Reference Singh and WaltherSW07, Lemma 2.5]. Then,
$v\otimes f^{1/p^{e}}\mapsto f^{1/p^{e}}\unicode[STIX]{x1D6FC}(v)$
is surjective [Reference Singh and WaltherSW07, Lemma 2.5]. Then,
is surjective. Thus,
![]() $\unicode[STIX]{x1D711}$
is surjective, because
$\unicode[STIX]{x1D711}$
is surjective, because
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D703}\circ (1\otimes \unicode[STIX]{x1D719})$
.
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D703}\circ (1\otimes \unicode[STIX]{x1D719})$
.
We have now that
![]() $\unicode[STIX]{x1D711}$
is surjective under the hypotheses assumed. Since
$\unicode[STIX]{x1D711}$
is surjective under the hypotheses assumed. Since
we have that
Then,
![]() $a_{i}(R)\leqslant p^{e}a_{d}(R)+\unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e}),$
and so
$a_{i}(R)\leqslant p^{e}a_{d}(R)+\unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e}),$
and so
![]() $(1-p^{e})a_{i}(R)\leqslant \unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e})$
. Hence,
$(1-p^{e})a_{i}(R)\leqslant \unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e})$
. Hence,
5 F-thresholds of graded Gorenstein rings
Suppose that
![]() $(R,\mathfrak{m},K)$
is an
$(R,\mathfrak{m},K)$
is an
![]() $F$
-finite standard graded Gorenstein
$F$
-finite standard graded Gorenstein
![]() $K$
-algebra. Let
$K$
-algebra. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
, and let
$S=K[x_{1},\ldots ,x_{n}]$
, and let
![]() $I\subseteq S$
be a homogeneous ideal such that
$I\subseteq S$
be a homogeneous ideal such that
![]() $R\cong S/I$
as graded rings. Since
$R\cong S/I$
as graded rings. Since
![]() $\operatorname{Hom}_{R}(R^{1/p},R)$
is a cyclic
$\operatorname{Hom}_{R}(R^{1/p},R)$
is a cyclic
![]() $R^{1/p}$
-module, we have that for all integers
$R^{1/p}$
-module, we have that for all integers
![]() $e\geqslant 1$
there exist homogeneous polynomials
$e\geqslant 1$
there exist homogeneous polynomials
![]() $f_{e}\in S$
such that
$f_{e}\in S$
such that
![]() $I^{[p^{e}]}:I=f_{e}S+I^{[p^{e}]}$
by Remark 2.10. In fact, if
$I^{[p^{e}]}:I=f_{e}S+I^{[p^{e}]}$
by Remark 2.10. In fact, if
![]() $I^{[p]}:I=fS+I^{[p]}$
, then
$I^{[p]}:I=fS+I^{[p]}$
, then
![]() $\displaystyle I^{[p^{e}]}:I=f^{(1+p+\cdots +p^{e-1})}S+I^{[p^{e}]}$
for all
$\displaystyle I^{[p^{e}]}:I=f^{(1+p+\cdots +p^{e-1})}S+I^{[p^{e}]}$
for all
![]() $e\geqslant 2$
.
$e\geqslant 2$
.
Remark 5.1. When
![]() $R=S/I$
is
$R=S/I$
is
![]() $F$
-pure, we have
$F$
-pure, we have
![]() $(I^{[p^{e}]}:I)\not \subseteq \mathfrak{n}^{[p^{e}]}$
by Fedder’s criterion. In the notation used above, if
$(I^{[p^{e}]}:I)\not \subseteq \mathfrak{n}^{[p^{e}]}$
by Fedder’s criterion. In the notation used above, if
![]() $(I^{[p^{e}]}:_{S}I)=f_{e}S+I^{[p^{e}]}$
for some homogeneous polynomial
$(I^{[p^{e}]}:_{S}I)=f_{e}S+I^{[p^{e}]}$
for some homogeneous polynomial
![]() $f_{e}$
, we get that
$f_{e}$
, we get that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \min \left\{s\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\min \left\{s\in \mathbb{N}~\bigg|\left[\frac{f_{e}S+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}=\deg (f_{e}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \min \left\{s\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\min \left\{s\in \mathbb{N}~\bigg|\left[\frac{f_{e}S+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}=\deg (f_{e}).\nonumber\end{eqnarray}$$
We now prove the last part of Theorem B.
Theorem 5.2. Let
![]() $(R,\mathfrak{m},K)$
be a Gorenstein standard graded
$(R,\mathfrak{m},K)$
be a Gorenstein standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure, and let
$F$
-pure, and let
![]() $d=\dim (R)$
. Then,
$d=\dim (R)$
. Then,
![]() $\operatorname{fpt}(R)=-a_{d}(R)$
.
$\operatorname{fpt}(R)=-a_{d}(R)$
.
Proof. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring, and let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring, and let
![]() $I\subseteq S$
be a homogeneous ideal such that
$I\subseteq S$
be a homogeneous ideal such that
![]() $R\cong S/I$
as graded rings. Let
$R\cong S/I$
as graded rings. Let
![]() $\mathfrak{n}=(x_{1},\ldots ,x_{n})$
, so that
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
, so that
![]() $\mathfrak{m}=\mathfrak{n}R$
. Let
$\mathfrak{m}=\mathfrak{n}R$
. Let
![]() $a=a_{d}(R)$
. Consider the natural map
$a=a_{d}(R)$
. Consider the natural map
![]() $S/I^{[p]}\rightarrow S/I$
induced by the inclusion
$S/I^{[p]}\rightarrow S/I$
induced by the inclusion
![]() $I^{[p]}\subseteq I$
. Then such a map extends to a map of complexes
$I^{[p]}\subseteq I$
. Then such a map extends to a map of complexes
![]() $\unicode[STIX]{x1D713}_{\bullet }$
from a minimal free resolution of
$\unicode[STIX]{x1D713}_{\bullet }$
from a minimal free resolution of
![]() $S/I^{[p]}$
to a minimal free resolution of
$S/I^{[p]}$
to a minimal free resolution of
![]() $S/I$
. Furthermore, such a map
$S/I$
. Furthermore, such a map
![]() $\unicode[STIX]{x1D713}_{\bullet }$
can be chosen graded of degree zero. We have that the last homomorphism in the map of complexes,
$\unicode[STIX]{x1D713}_{\bullet }$
can be chosen graded of degree zero. We have that the last homomorphism in the map of complexes,
![]() $S(p(-n-a))\rightarrow S(-n-a)$
is given by multiplication by a homogeneous polynomial
$S(p(-n-a))\rightarrow S(-n-a)$
is given by multiplication by a homogeneous polynomial
![]() $f$
(see Remark 6.6). Furthermore,
$f$
(see Remark 6.6). Furthermore,
![]() $I^{[p]}:I=fS+I^{[p]}$
[Reference VraciuVra03, Lemma 1]. Since
$I^{[p]}:I=fS+I^{[p]}$
[Reference VraciuVra03, Lemma 1]. Since
![]() $\unicode[STIX]{x1D713}_{\bullet }$
is homogeneous of degree zero, we have that
$\unicode[STIX]{x1D713}_{\bullet }$
is homogeneous of degree zero, we have that
![]() $\deg (f)=(p-1)(n+a)$
.
$\deg (f)=(p-1)(n+a)$
.
Recall that, for all
![]() $e\geqslant 2$
, we have that
$e\geqslant 2$
, we have that
![]() $(I^{[p^{e}]}:_{S}I)=f^{(1+p+\cdots +p^{e-1})}S+I^{[p^{e}]}$
. By Remark 5.1 and Lemma 4.2, we obtain that
$(I^{[p^{e}]}:_{S}I)=f^{(1+p+\cdots +p^{e-1})}S+I^{[p^{e}]}$
. By Remark 5.1 and Lemma 4.2, we obtain that
 $$\begin{eqnarray}\displaystyle \hspace{31.0001pt}\operatorname{fpt}(R) & = & \displaystyle \lim _{e\rightarrow \infty }\frac{n(p^{e}-1)-(\deg (f)\cdot (1+p+\cdots +p^{e-1}))}{p^{e}}\nonumber\\ \displaystyle & = & \displaystyle \lim _{e\rightarrow \infty }\frac{n(p^{e}-1)}{p^{e}}-\lim _{e\rightarrow \infty }\frac{\deg (f)\cdot (1+p+\cdots +p^{e-1})}{p^{e}}\nonumber\\ \displaystyle & = & \displaystyle n-\frac{\deg (f)}{p-1}\nonumber\\ \displaystyle & = & \displaystyle n-\frac{(p-1)(n+a)}{p-1}\nonumber\\ \displaystyle & = & \displaystyle -a.\hspace{211.00038pt}\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hspace{31.0001pt}\operatorname{fpt}(R) & = & \displaystyle \lim _{e\rightarrow \infty }\frac{n(p^{e}-1)-(\deg (f)\cdot (1+p+\cdots +p^{e-1}))}{p^{e}}\nonumber\\ \displaystyle & = & \displaystyle \lim _{e\rightarrow \infty }\frac{n(p^{e}-1)}{p^{e}}-\lim _{e\rightarrow \infty }\frac{\deg (f)\cdot (1+p+\cdots +p^{e-1})}{p^{e}}\nonumber\\ \displaystyle & = & \displaystyle n-\frac{\deg (f)}{p-1}\nonumber\\ \displaystyle & = & \displaystyle n-\frac{(p-1)(n+a)}{p-1}\nonumber\\ \displaystyle & = & \displaystyle -a.\hspace{211.00038pt}\square\nonumber\end{eqnarray}$$
We now give an example to show that an
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure standard graded
$F$
-pure standard graded
![]() $K$
-algebra such that
$K$
-algebra such that
![]() $\operatorname{fpt}(R)=-a_{d}(R)$
is not necessarily Gorenstein. This is not a counterexample to Conjecture A(2), since the ring we consider is not strongly
$\operatorname{fpt}(R)=-a_{d}(R)$
is not necessarily Gorenstein. This is not a counterexample to Conjecture A(2), since the ring we consider is not strongly
![]() $F$
-regular.
$F$
-regular.
Example 5.3. Let
![]() $S=K[x,y,z]$
with
$S=K[x,y,z]$
with
![]() $K$
a perfect field of characteristic
$K$
a perfect field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $\mathfrak{n}=(x,y,z)$
be its homogeneous maximal ideal.
$\mathfrak{n}=(x,y,z)$
be its homogeneous maximal ideal.
Let
![]() $R=S/I$
, with maximal ideal
$R=S/I$
, with maximal ideal
![]() $\mathfrak{m}=\mathfrak{n}/I$
. Note that
$\mathfrak{m}=\mathfrak{n}/I$
. Note that
![]() $R$
is a one-dimensional Cohen–Macaulay
$R$
is a one-dimensional Cohen–Macaulay
![]() $F$
-pure ring. In addition,
$F$
-pure ring. In addition,
![]() ${\mathcal{P}}(R)=(x,y,z)R$
; therefore,
${\mathcal{P}}(R)=(x,y,z)R$
; therefore,
![]() $\operatorname{sdim}(R)=0$
and, by Theorem 4.7,
$\operatorname{sdim}(R)=0$
and, by Theorem 4.7,
![]() $\operatorname{fpt}(R)=0$
as well. On the other hand, from the short exact sequence
$\operatorname{fpt}(R)=0$
as well. On the other hand, from the short exact sequence
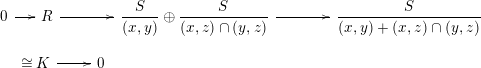
we get a long exact sequence of local cohomology modules
![]()
The maps in this sequence are homogeneous of degree zero. Thus,
![]() $a_{1}(R)\geqslant 0$
, because
$a_{1}(R)\geqslant 0$
, because
![]() $K$
injects into
$K$
injects into
![]() $H_{\mathfrak{m}}^{1}(R)$
. On the other hand, since
$H_{\mathfrak{m}}^{1}(R)$
. On the other hand, since
![]() $R$
is
$R$
is
![]() $F$
-pure, we have that
$F$
-pure, we have that
![]() $a_{1}(R)\leqslant 0$
; therefore,
$a_{1}(R)\leqslant 0$
; therefore,
![]() $\operatorname{fpt}(R)=a_{1}(R)=0$
. Although
$\operatorname{fpt}(R)=a_{1}(R)=0$
. Although
![]() $R$
is not Gorenstein, since the canonical module
$R$
is not Gorenstein, since the canonical module
![]() $\unicode[STIX]{x1D714}_{R}\cong (x,y)/(xy,xz+yz)$
has two generators.
$\unicode[STIX]{x1D714}_{R}\cong (x,y)/(xy,xz+yz)$
has two generators.
Sannai and Watanabe [Reference Sannai and WatanabeSW11, Theorem 4.2] showed that for an
![]() $F$
-pure standard graded Gorenstein algebra,
$F$
-pure standard graded Gorenstein algebra,
![]() $R$
, with an isolated singularity,
$R$
, with an isolated singularity,
![]() $\operatorname{sdim}(R)=0$
is equivalent to
$\operatorname{sdim}(R)=0$
is equivalent to
![]() $a_{d}(R)=0.$
The previous theorem recovers this result dropping the hypothesis of isolated singularity. This is because
$a_{d}(R)=0.$
The previous theorem recovers this result dropping the hypothesis of isolated singularity. This is because
![]() $\operatorname{sdim}(R)=0$
is equivalent to
$\operatorname{sdim}(R)=0$
is equivalent to
![]() $\operatorname{fpt}(R)=0.$
In fact, for all
$\operatorname{fpt}(R)=0.$
In fact, for all
![]() $F$
-pure rings, Corollary 4.4 shows that
$F$
-pure rings, Corollary 4.4 shows that
![]() $a_{d}(R)=0$
implies
$a_{d}(R)=0$
implies
![]() $\operatorname{sdim}(R)=0.$
$\operatorname{sdim}(R)=0.$
We now aim at an interpretation of the
![]() $F$
-pure threshold of a standard graded Gorenstein
$F$
-pure threshold of a standard graded Gorenstein
![]() $K$
-algebra as the maximal length of a regular sequence that preserves
$K$
-algebra as the maximal length of a regular sequence that preserves
![]() $F$
-purity.
$F$
-purity.
Proposition 5.4. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
![]() $F$
-finite infinite field
$F$
-finite infinite field
![]() $K$
. Let
$K$
. Let
![]() $\mathfrak{n}=(x_{1},\ldots ,x_{n})$
denote the maximal homogeneous ideal. Let
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
denote the maximal homogeneous ideal. Let
![]() $I\subseteq S$
be a homogeneous ideal such that
$I\subseteq S$
be a homogeneous ideal such that
![]() $R=S/I$
is an
$R=S/I$
is an
![]() $F$
-pure ring, and let
$F$
-pure ring, and let
![]() $\mathfrak{m}=\mathfrak{n}R$
. Let
$\mathfrak{m}=\mathfrak{n}R$
. Let
![]() $f\in (I^{[p]}:I)\smallsetminus \mathfrak{n}^{[p]}$
. If
$f\in (I^{[p]}:I)\smallsetminus \mathfrak{n}^{[p]}$
. If
![]() $\deg (f)\leqslant (p-1)(n-1)$
, then there exists a linear form
$\deg (f)\leqslant (p-1)(n-1)$
, then there exists a linear form
![]() $\ell \in S$
such that:
$\ell \in S$
such that:
-
(1)
 $\ell ^{p-1}f\not \in \mathfrak{n}^{[p]}$
.
$\ell ^{p-1}f\not \in \mathfrak{n}^{[p]}$
. -
(2) the class of
 $\ell$
in
$\ell$
in
 $R$
does not belong to
$R$
does not belong to
 ${\mathcal{P}}(R)$
.
${\mathcal{P}}(R)$
. -
(3)
 $\ell$
is a nonzero divisor in
$\ell$
is a nonzero divisor in
 $R$
.
$R$
. -
(4) The ring
 $S/(I+(\ell ))$
is
$S/(I+(\ell ))$
is
 $F$
-pure.
$F$
-pure.
Proof. Let us pick
![]() $c_{\unicode[STIX]{x1D6FC}}\in K$
such that
$c_{\unicode[STIX]{x1D6FC}}\in K$
such that
![]() $f=\sum _{|\unicode[STIX]{x1D6FC}|=\deg (f)}c_{\unicode[STIX]{x1D6FC}}x^{\unicode[STIX]{x1D6FC}}$
. Let
$f=\sum _{|\unicode[STIX]{x1D6FC}|=\deg (f)}c_{\unicode[STIX]{x1D6FC}}x^{\unicode[STIX]{x1D6FC}}$
. Let
be a generic linear form. We note that
where
![]() $g_{\unicode[STIX]{x1D703}}(y)=(p-1)!/\unicode[STIX]{x1D703}_{1}!\cdots \unicode[STIX]{x1D703}_{n}!y^{\unicode[STIX]{x1D703}}\in K[y_{1},\ldots ,y_{n}]$
.
$g_{\unicode[STIX]{x1D703}}(y)=(p-1)!/\unicode[STIX]{x1D703}_{1}!\cdots \unicode[STIX]{x1D703}_{n}!y^{\unicode[STIX]{x1D703}}\in K[y_{1},\ldots ,y_{n}]$
.
Since
![]() $f\not \in \mathfrak{n}^{[p]},$
there exists
$f\not \in \mathfrak{n}^{[p]},$
there exists
![]() $x^{\unicode[STIX]{x1D6FD}}\in \operatorname{Supp}\{f\}$
such that
$x^{\unicode[STIX]{x1D6FD}}\in \operatorname{Supp}\{f\}$
such that
![]() $x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
. Since
$x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
. Since
![]() $|\unicode[STIX]{x1D6FD}|\leqslant (p-1)(n-1)$
and
$|\unicode[STIX]{x1D6FD}|\leqslant (p-1)(n-1)$
and
![]() $x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
, there exists
$x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
, there exists
![]() $x^{\unicode[STIX]{x1D6FE}}\in \mathfrak{n}^{p-1}$
such that
$x^{\unicode[STIX]{x1D6FE}}\in \mathfrak{n}^{p-1}$
such that
![]() $x^{\unicode[STIX]{x1D6FE}}x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
by Pigeonhole principle. Let
$x^{\unicode[STIX]{x1D6FE}}x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
by Pigeonhole principle. Let
We note that
![]() $h\neq 0$
because
$h\neq 0$
because
![]() $c_{\unicode[STIX]{x1D6FD}}g_{\unicode[STIX]{x1D703}}\neq 0$
. In addition,
$c_{\unicode[STIX]{x1D6FD}}g_{\unicode[STIX]{x1D703}}\neq 0$
. In addition,
![]() $h$
is the coefficient of
$h$
is the coefficient of
![]() $x^{\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FE}}$
in
$x^{\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FE}}$
in
![]() $\left(\ell _{y}\right)^{p-1}f$
. We note that
$\left(\ell _{y}\right)^{p-1}f$
. We note that
![]() ${\mathcal{P}}(R)\neq \mathfrak{m}$
by Lemma 4.1, and thus
${\mathcal{P}}(R)\neq \mathfrak{m}$
by Lemma 4.1, and thus
![]() ${\mathcal{P}}(R)\cap \mathfrak{m}\neq \mathfrak{m}$
. Since
${\mathcal{P}}(R)\cap \mathfrak{m}\neq \mathfrak{m}$
. Since
![]() $K$
is an infinite field, we can pick a point
$K$
is an infinite field, we can pick a point
![]() $v\in K^{n}$
such that
$v\in K^{n}$
such that
![]() $h(v)\neq 0$
and the class of
$h(v)\neq 0$
and the class of
![]() $\ell _{y}(v)$
does not belong to
$\ell _{y}(v)$
does not belong to
![]() ${\mathcal{P}}(R)$
. We set
${\mathcal{P}}(R)$
. We set
![]() $\ell =\ell _{y}(v).$
By our construction of
$\ell =\ell _{y}(v).$
By our construction of
![]() $\ell$
,
$\ell$
,
![]() $x^{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}\in \operatorname{Supp}\{\ell ^{p-1}f\}$
and
$x^{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}\in \operatorname{Supp}\{\ell ^{p-1}f\}$
and
![]() $x^{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}\not \in \mathfrak{n}^{[p]}$
. In addition,
$x^{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}\not \in \mathfrak{n}^{[p]}$
. In addition,
![]() $\ell \notin {\mathcal{P}}(R).$
Since the pullback of
$\ell \notin {\mathcal{P}}(R).$
Since the pullback of
![]() ${\mathcal{P}}(R)$
to
${\mathcal{P}}(R)$
to
![]() $S$
contains every associated prime of
$S$
contains every associated prime of
![]() $R$
, we have that
$R$
, we have that
![]() $\ell$
is a nonzero divisor in
$\ell$
is a nonzero divisor in
![]() $R$
. To show the last claim we note that, setting
$R$
. To show the last claim we note that, setting
![]() $I^{\prime }:=I+(\ell )$
, we have that
$I^{\prime }:=I+(\ell )$
, we have that
![]() $\ell ^{p-1}f\in ({I^{\prime }}^{[p]}:I^{\prime })\smallsetminus \mathfrak{n}^{[p]}$
, and
$\ell ^{p-1}f\in ({I^{\prime }}^{[p]}:I^{\prime })\smallsetminus \mathfrak{n}^{[p]}$
, and
![]() $F$
-purity follows by Fedder’s criterion [Reference FedderFed83, Theorem 1.12].◻
$F$
-purity follows by Fedder’s criterion [Reference FedderFed83, Theorem 1.12].◻
As a consequence of these results, and of Theorem 5.2, we give an interpretation of the
![]() $F$
-pure threshold, and the
$F$
-pure threshold, and the
![]() $a$
-invariant, in terms of the maximal length of a regular sequence that preserves
$a$
-invariant, in terms of the maximal length of a regular sequence that preserves
![]() $F$
-purity. We start by introducing the concept of
$F$
-purity. We start by introducing the concept of
![]() $F$
-pure regular sequence.
$F$
-pure regular sequence.
Definition 5.5. Let
![]() $R$
be an
$R$
be an
![]() $F$
-finite
$F$
-finite
![]() $F$
-pure ring. We say that a regular sequence
$F$
-pure ring. We say that a regular sequence
![]() $f_{1},\ldots ,f_{r}$
is
$f_{1},\ldots ,f_{r}$
is
![]() $F$
-pure if
$F$
-pure if
![]() $R/(f_{1},\ldots ,f_{i})$
is an
$R/(f_{1},\ldots ,f_{i})$
is an
![]() $F$
-pure ring for all
$F$
-pure ring for all
![]() $i=1,\ldots ,r.$
$i=1,\ldots ,r.$
Lemma 5.6. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra. If
$K$
-algebra. If
![]() $f$
is a regular element of degree
$f$
is a regular element of degree
![]() $d>0$
, then
$d>0$
, then
![]() $d+a_{i}(R)\leqslant a_{i-1}(R/(f))$
for all
$d+a_{i}(R)\leqslant a_{i-1}(R/(f))$
for all
![]() $i\in \mathbb{N}$
such that
$i\in \mathbb{N}$
such that
![]() $H_{\mathfrak{m}}^{i}(R)\neq 0$
.
$H_{\mathfrak{m}}^{i}(R)\neq 0$
.
Proof. Suppose that
![]() $H_{\mathfrak{m}}^{i}(R)\neq 0$
. Consider the homogeneous short exact sequence
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. Consider the homogeneous short exact sequence
![]()
For all
![]() $j\in \mathbb{Z}$
, this gives rise to an exact sequence of
$j\in \mathbb{Z}$
, this gives rise to an exact sequence of
![]() $K$
-vector spaces
$K$
-vector spaces
![]()
Since
![]() $d>0$
, for
$d>0$
, for
![]() $j=a_{i}(R)+d$
we have that
$j=a_{i}(R)+d$
we have that
![]() $H_{\mathfrak{m}}^{i}(R)_{j}=0$
. Then,
$H_{\mathfrak{m}}^{i}(R)_{j}=0$
. Then,
![]()
is a surjection. We note that
![]() $H_{\mathfrak{m}}^{i}(R)_{a_{i}(R)}\neq 0$
, which yields
$H_{\mathfrak{m}}^{i}(R)_{a_{i}(R)}\neq 0$
, which yields
and hence
![]() $a_{i-1}(R/(f))\geqslant a_{i}(R)+d$
.◻
$a_{i-1}(R/(f))\geqslant a_{i}(R)+d$
.◻
Corollary 5.7. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure. If
$F$
-pure. If
![]() $f_{1},\ldots ,f_{r}$
is a homogeneous
$f_{1},\ldots ,f_{r}$
is a homogeneous
![]() $F$
-pure regular sequence of degrees
$F$
-pure regular sequence of degrees
![]() $d_{1},\ldots ,d_{r}$
, then
$d_{1},\ldots ,d_{r}$
, then
![]() $\sum _{j=1}^{r}d_{j}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
.
$\sum _{j=1}^{r}d_{j}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
.
Proof. We proceed by induction on
![]() $r\geqslant 1$
. Assume that
$r\geqslant 1$
. Assume that
![]() $r=1$
. If
$r=1$
. If
![]() $H_{\mathfrak{m}}^{i}(R)=0$
, we have that
$H_{\mathfrak{m}}^{i}(R)=0$
, we have that
![]() $d_{1}\leqslant -a_{i}(R)=\infty$
, therefore there is nothing to prove in this case. If
$d_{1}\leqslant -a_{i}(R)=\infty$
, therefore there is nothing to prove in this case. If
![]() $H_{\mathfrak{m}}^{i}(R)\neq 0$
, by Lemma 5.6 we have that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
, by Lemma 5.6 we have that
![]() $a_{i}(R)+d_{1}\leqslant a_{i-1}(R/(f_{1}))$
. Since
$a_{i}(R)+d_{1}\leqslant a_{i-1}(R/(f_{1}))$
. Since
![]() $R/(f_{1})$
is
$R/(f_{1})$
is
![]() $F$
-pure, it follows from Remark 2.5 that
$F$
-pure, it follows from Remark 2.5 that
![]() $a_{i-1}(R/(f))\leqslant 0$
, and hence
$a_{i-1}(R/(f))\leqslant 0$
, and hence
![]() $d_{1}\leqslant -a_{i}(R)$
. Thus,
$d_{1}\leqslant -a_{i}(R)$
. Thus,
![]() $d_{1}\leqslant -a_{i}(R)$
for all
$d_{1}\leqslant -a_{i}(R)$
for all
![]() $i\in \mathbb{N}$
, that is,
$i\in \mathbb{N}$
, that is,
![]() $d_{1}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
. This concludes the proof of the base case. For
$d_{1}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
. This concludes the proof of the base case. For
![]() $r>1$
, if
$r>1$
, if
![]() $H_{\mathfrak{m}}^{i}(R)=0$
we have that
$H_{\mathfrak{m}}^{i}(R)=0$
we have that
![]() $\sum _{i=1}^{r}d_{i}\leqslant -a_{i}(R)=\infty$
and, again, there is nothing to prove in this case. Assume that
$\sum _{i=1}^{r}d_{i}\leqslant -a_{i}(R)=\infty$
and, again, there is nothing to prove in this case. Assume that
![]() $H_{\mathfrak{m}}^{i}(R)\neq 0$
. By induction, we get that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. By induction, we get that
![]() $\sum _{j=2}^{r}d_{j}\leqslant -a_{s}(R/(f_{1}))$
for all
$\sum _{j=2}^{r}d_{j}\leqslant -a_{s}(R/(f_{1}))$
for all
![]() $s\in \mathbb{N}$
. In particular, we have that
$s\in \mathbb{N}$
. In particular, we have that
![]() $\sum _{j=2}^{r}d_{j}\leqslant -a_{i-1}(R/(f_{1}))$
. By Lemma 5.6, we have that
$\sum _{j=2}^{r}d_{j}\leqslant -a_{i-1}(R/(f_{1}))$
. By Lemma 5.6, we have that
![]() $-a_{i-1}(R/(f_{1}))\geqslant -a_{i}(R)-d_{1}$
. Combining the two inequalities, and rearranging the terms in the sum, we obtain
$-a_{i-1}(R/(f_{1}))\geqslant -a_{i}(R)-d_{1}$
. Combining the two inequalities, and rearranging the terms in the sum, we obtain
![]() $\sum _{j=1}^{r}d_{i}\leqslant -a_{i}(R)$
. Therefore, we obtain
$\sum _{j=1}^{r}d_{i}\leqslant -a_{i}(R)$
. Therefore, we obtain
![]() $\sum _{j=1}^{r}d_{j}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
.◻
$\sum _{j=1}^{r}d_{j}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
.◻
Theorem 5.8. Let
![]() $(R,\mathfrak{m},K)$
be a Gorenstein standard graded
$(R,\mathfrak{m},K)$
be a Gorenstein standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure, and let
$F$
-pure, and let
![]() $d=\dim (R)$
. If
$d=\dim (R)$
. If
![]() $f_{1},\ldots ,f_{r}$
is an
$f_{1},\ldots ,f_{r}$
is an
![]() $F$
-pure regular sequence, then
$F$
-pure regular sequence, then
![]() $r\leqslant \operatorname{fpt}(R)$
. Furthermore, if
$r\leqslant \operatorname{fpt}(R)$
. Furthermore, if
![]() $K$
is infinite, then there exists an
$K$
is infinite, then there exists an
![]() $F$
-pure regular sequence consisting of
$F$
-pure regular sequence consisting of
![]() $\operatorname{fpt}(R)$
linear forms.
$\operatorname{fpt}(R)$
linear forms.
Proof. By Theorem 5.2, we have that
![]() $\operatorname{fpt}(R)=-a_{d}(R)$
. The first claim follows from Corollary 5.7. For the second claim, let
$\operatorname{fpt}(R)=-a_{d}(R)$
. The first claim follows from Corollary 5.7. For the second claim, let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring and let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring and let
![]() $I\subseteq S$
be a homogeneous ideal such that
$I\subseteq S$
be a homogeneous ideal such that
![]() $R\cong S/I$
as graded rings. We proceed by induction on
$R\cong S/I$
as graded rings. We proceed by induction on
![]() $\operatorname{fpt}(R)$
. The case
$\operatorname{fpt}(R)$
. The case
![]() $\operatorname{fpt}(R)=0$
is trivial. We now assume
$\operatorname{fpt}(R)=0$
is trivial. We now assume
![]() $\operatorname{fpt}(R)>0$
. From the proof of Theorem 5.2, we have that
$\operatorname{fpt}(R)>0$
. From the proof of Theorem 5.2, we have that
![]() $(I^{[p]}:_{S}I)=fS+I^{[p]}$
for a homogeneous polynomial
$(I^{[p]}:_{S}I)=fS+I^{[p]}$
for a homogeneous polynomial
![]() $f\in (I^{[p]}:_{S}I)\smallsetminus \mathfrak{n}^{[p]}$
of degree
$f\in (I^{[p]}:_{S}I)\smallsetminus \mathfrak{n}^{[p]}$
of degree
![]() $\deg (f)\leqslant (p-1)(n+a_{d}(R))$
. Since
$\deg (f)\leqslant (p-1)(n+a_{d}(R))$
. Since
![]() $a_{d}(R)=-\operatorname{fpt}(R)<0$
by assumption, there exists a linear nonzero divisor
$a_{d}(R)=-\operatorname{fpt}(R)<0$
by assumption, there exists a linear nonzero divisor
![]() $\ell _{1}\in R$
such that
$\ell _{1}\in R$
such that
![]() $R/(\ell _{1})$
is
$R/(\ell _{1})$
is
![]() $F$
-pure by Proposition 5.4. Note that, from the homogeneous short exact sequence
$F$
-pure by Proposition 5.4. Note that, from the homogeneous short exact sequence
![]()
it follows that
![]() $a_{d-1}(R/(\ell _{1}))=a_{d}(R)+1$
. Since
$a_{d-1}(R/(\ell _{1}))=a_{d}(R)+1$
. Since
![]() $R/(\ell _{1})$
is Gorenstein, we have that
$R/(\ell _{1})$
is Gorenstein, we have that
![]() $\operatorname{fpt}(R/(\ell _{1}))=-a_{d-1}(R/(\ell _{1}))=-a_{d}(R)-1=\operatorname{fpt}(R)-1$
. The claim follows by induction.◻
$\operatorname{fpt}(R/(\ell _{1}))=-a_{d-1}(R/(\ell _{1}))=-a_{d}(R)-1=\operatorname{fpt}(R)-1$
. The claim follows by induction.◻
6 Results in characteristic zero
In this section we present results in characteristic zero that are analogous to Theorem 4.3. These results are motivated by the relation between the log-canonical and the
![]() $F$
-pure threshold.
$F$
-pure threshold.
We first fix the notation. Let
![]() $K$
be a field of characteristic zero, and let
$K$
be a field of characteristic zero, and let
![]() $(R,\mathfrak{m},K)$
be a
$(R,\mathfrak{m},K)$
be a
![]() $\mathbb{Q}$
-Gorenstein normal standard graded
$\mathbb{Q}$
-Gorenstein normal standard graded
![]() $K$
-algebra. Consider the closed subscheme
$K$
-algebra. Consider the closed subscheme
![]() $V(\mathfrak{m})=Y\subseteq X=\operatorname{Spec}(R)$
, and let
$V(\mathfrak{m})=Y\subseteq X=\operatorname{Spec}(R)$
, and let
![]() $\mathfrak{a}$
be the corresponding ideal sheaf. We now use Hironaka’s resolution of singularities [Reference HironakaHir64]. Suppose that
$\mathfrak{a}$
be the corresponding ideal sheaf. We now use Hironaka’s resolution of singularities [Reference HironakaHir64]. Suppose that
![]() $f:\widetilde{X}\rightarrow X$
is a log-resolution of the pair
$f:\widetilde{X}\rightarrow X$
is a log-resolution of the pair
![]() $(X,Y)$
, that is,
$(X,Y)$
, that is,
![]() $f$
is a proper birational morphism with
$f$
is a proper birational morphism with
![]() $\widetilde{X}$
nonsingular such that the ideal sheaf
$\widetilde{X}$
nonsingular such that the ideal sheaf
![]() $\mathfrak{a}{\mathcal{O}}_{\widetilde{X}}={\mathcal{O}}_{\widetilde{X}}(-F)$
is invertible, and
$\mathfrak{a}{\mathcal{O}}_{\widetilde{X}}={\mathcal{O}}_{\widetilde{X}}(-F)$
is invertible, and
![]() $\operatorname{Supp}(F)\cup \text{Exc}(f)$
is a simple normal crossing divisor. Let
$\operatorname{Supp}(F)\cup \text{Exc}(f)$
is a simple normal crossing divisor. Let
![]() $K_{X}$
and
$K_{X}$
and
![]() $K_{\widetilde{X}}$
denote canonical divisors of X and
$K_{\widetilde{X}}$
denote canonical divisors of X and
![]() $\widetilde{X}$
, respectively.
$\widetilde{X}$
, respectively.
Let
![]() $\unicode[STIX]{x1D706}\geqslant 0$
be a real number. Then there are finitely many irreducible (not necessarily exceptional) divisors
$\unicode[STIX]{x1D706}\geqslant 0$
be a real number. Then there are finitely many irreducible (not necessarily exceptional) divisors
![]() $E_{i}$
on
$E_{i}$
on
![]() $\widetilde{X}$
and real numbers
$\widetilde{X}$
and real numbers
![]() $a_{i}$
so that there exists an
$a_{i}$
so that there exists an
![]() $\mathbb{R}$
-linear equivalence of
$\mathbb{R}$
-linear equivalence of
![]() $\mathbb{R}$
-divisors
$\mathbb{R}$
-divisors
Definition 6.1. Continuing with the previous notation, we say that the pair
![]() $(X,\unicode[STIX]{x1D706}Y)$
is log-canonical, or lc for short, if
$(X,\unicode[STIX]{x1D706}Y)$
is log-canonical, or lc for short, if
![]() $a_{i}\geqslant -1$
for all
$a_{i}\geqslant -1$
for all
![]() $i$
. Define
$i$
. Define
We say that
![]() $(X,\unicode[STIX]{x1D706}Y)$
is Kawamata log-terminal, or klt for short, if
$(X,\unicode[STIX]{x1D706}Y)$
is Kawamata log-terminal, or klt for short, if
![]() $a_{i}>-1$
for all
$a_{i}>-1$
for all
![]() $i.$
$i.$
Remark 6.2. If
![]() $X$
is log-terminal, we have that
$X$
is log-terminal, we have that
Definition 6.3. Let
![]() $K$
be a field of positive characteristic
$K$
be a field of positive characteristic
![]() $p$
, and let
$p$
, and let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-pure. Let
$F$
-pure. Let
![]() $I\subseteq R$
be a homogeneous ideal. For a real number
$I\subseteq R$
be a homogeneous ideal. For a real number
![]() $\unicode[STIX]{x1D706}\geqslant 0$
, we say that
$\unicode[STIX]{x1D706}\geqslant 0$
, we say that
![]() $(R,I^{\unicode[STIX]{x1D706}})$
is strongly
$(R,I^{\unicode[STIX]{x1D706}})$
is strongly
![]() $F$
-regular if for every
$F$
-regular if for every
![]() $c\in R$
not in any minimal prime, there exists
$c\in R$
not in any minimal prime, there exists
![]() $e\geqslant 0$
and an element
$e\geqslant 0$
and an element
![]() $f\in I^{\lceil p^{e}\unicode[STIX]{x1D706}\rceil }$
such that the inclusion of
$f\in I^{\lceil p^{e}\unicode[STIX]{x1D706}\rceil }$
such that the inclusion of
![]() $R$
-modules
$R$
-modules
![]() $(cf)^{1/p^{e}}R\subseteq R^{1/p^{e}}$
splits.
$(cf)^{1/p^{e}}R\subseteq R^{1/p^{e}}$
splits.
Remark 6.4. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded
$(R,\mathfrak{m},K)$
be a standard graded
![]() $K$
-algebra which is
$K$
-algebra which is
![]() $F$
-finite and strongly
$F$
-finite and strongly
![]() $F$
-regular. Then, by [Reference Takagi and WatanabeTW04, Proposition 2.2(5)], we have
$F$
-regular. Then, by [Reference Takagi and WatanabeTW04, Proposition 2.2(5)], we have
Definition 6.5. Let
![]() $R$
be a reduced algebra essentially of finite type over a field
$R$
be a reduced algebra essentially of finite type over a field
![]() $K$
of characteristic zero,
$K$
of characteristic zero,
![]() $\mathfrak{a}\subseteq R$
an ideal, and
$\mathfrak{a}\subseteq R$
an ideal, and
![]() $\unicode[STIX]{x1D706}>0$
a real number. The pair
$\unicode[STIX]{x1D706}>0$
a real number. The pair
![]() $(R,\mathfrak{a}^{\unicode[STIX]{x1D706}})$
is said to be of dense
$(R,\mathfrak{a}^{\unicode[STIX]{x1D706}})$
is said to be of dense
![]() $F$
-pure type (respectively strongly
$F$
-pure type (respectively strongly
![]() $F$
-regular type) if there exist a finitely generated
$F$
-regular type) if there exist a finitely generated
![]() $\mathbb{Z}$
-subalgebra
$\mathbb{Z}$
-subalgebra
![]() $A$
of
$A$
of
![]() $K$
and a reduced subalgebra
$K$
and a reduced subalgebra
![]() $R_{A}$
of
$R_{A}$
of
![]() $R$
essentially of finite type over
$R$
essentially of finite type over
![]() $A$
which satisfy the following conditions:
$A$
which satisfy the following conditions:
-
(i)
 $R_{A}$
is flat over
$R_{A}$
is flat over
 $A$
,
$A$
,
 $R_{A}\otimes _{A}K\cong R$
, and
$R_{A}\otimes _{A}K\cong R$
, and
 $\mathfrak{a}_{A}R=\mathfrak{a}$
, where
$\mathfrak{a}_{A}R=\mathfrak{a}$
, where
 $\mathfrak{a}_{A}=\mathfrak{a}\cap R_{A}\subseteq R_{A}$
.
$\mathfrak{a}_{A}=\mathfrak{a}\cap R_{A}\subseteq R_{A}$
. -
(ii) The pair
 $(R_{s},\mathfrak{a}_{s}^{\unicode[STIX]{x1D706}})$
is
$(R_{s},\mathfrak{a}_{s}^{\unicode[STIX]{x1D706}})$
is
 $F$
-pure (respectively strongly
$F$
-pure (respectively strongly
 $F$
-regular) for every closed point
$F$
-regular) for every closed point
 $s$
in a dense subset of
$s$
in a dense subset of
 $\operatorname{Spec}(A)$
. Here, if
$\operatorname{Spec}(A)$
. Here, if
 $\unicode[STIX]{x1D705}(s)$
denotes the residue field of
$\unicode[STIX]{x1D705}(s)$
denotes the residue field of
 $s$
, we define
$s$
, we define
 $R_{s}=R_{A}\otimes _{A}\unicode[STIX]{x1D705}(s)$
and
$R_{s}=R_{A}\otimes _{A}\unicode[STIX]{x1D705}(s)$
and
 $\mathfrak{a}_{s}=\mathfrak{a}_{A}R_{s}\subseteq R_{s}$
.
$\mathfrak{a}_{s}=\mathfrak{a}_{A}R_{s}\subseteq R_{s}$
.
Remark 6.6. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field
![]() $K$
, and
$K$
, and
![]() $I\subseteq S$
be a homogeneous ideal. Let
$I\subseteq S$
be a homogeneous ideal. Let
![]() $R=S/I$
, and consider a minimal graded free resolution of
$R=S/I$
, and consider a minimal graded free resolution of
![]() $R$
over
$R$
over
![]() $S$
$S$
![]()
If we write
![]() $G_{n-d}=\bigoplus _{j}S(-j)^{\unicode[STIX]{x1D6FD}_{n-d,j}(R)}$
, where the positive integers
$G_{n-d}=\bigoplus _{j}S(-j)^{\unicode[STIX]{x1D6FD}_{n-d,j}(R)}$
, where the positive integers
![]() $\unicode[STIX]{x1D6FD}_{n-d,j}(R)$
are the
$\unicode[STIX]{x1D6FD}_{n-d,j}(R)$
are the
![]() $(n-d)$
th graded Betti numbers of
$(n-d)$
th graded Betti numbers of
![]() $R$
over
$R$
over
![]() $S$
, we have that
$S$
, we have that
![]() $\max \{j\mid \unicode[STIX]{x1D6FD}_{n-d,j}(R)\neq 0\}=-n-a_{d}(R)$
[Reference Bruns and HerzogBH93, Section 3.6]. Therefore, when
$\max \{j\mid \unicode[STIX]{x1D6FD}_{n-d,j}(R)\neq 0\}=-n-a_{d}(R)$
[Reference Bruns and HerzogBH93, Section 3.6]. Therefore, when
![]() $R$
is Cohen–Macaulay,
$R$
is Cohen–Macaulay,
![]() $a_{d}(R)$
can be read from the graded Betti numbers of
$a_{d}(R)$
can be read from the graded Betti numbers of
![]() $R$
over
$R$
over
![]() $S$
.
$S$
.
Lemma 6.7. Let
![]() $(R,\mathfrak{m},K)$
be a Cohen–Macaulay standard graded
$(R,\mathfrak{m},K)$
be a Cohen–Macaulay standard graded
![]() $K$
-algebra of dimension
$K$
-algebra of dimension
![]() $d$
, with
$d$
, with
![]() $K$
a field of characteristic zero, and let
$K$
a field of characteristic zero, and let
![]() $A$
be a finitely generated
$A$
be a finitely generated
![]() $\mathbb{Z}$
-subalgebra of
$\mathbb{Z}$
-subalgebra of
![]() $K$
. Assume that
$K$
. Assume that
![]() $R_{0}$
is a graded
$R_{0}$
is a graded
![]() $A$
-algebra such that
$A$
-algebra such that
![]() $R_{0}\otimes _{A}K\cong R$
as graded rings. For a closed point
$R_{0}\otimes _{A}K\cong R$
as graded rings. For a closed point
![]() $s\in \operatorname{Max}\operatorname{Spec}(A)$
, let
$s\in \operatorname{Max}\operatorname{Spec}(A)$
, let
![]() $R_{s}=R_{0}\otimes _{A}\unicode[STIX]{x1D705}(s)$
, where
$R_{s}=R_{0}\otimes _{A}\unicode[STIX]{x1D705}(s)$
, where
![]() $\unicode[STIX]{x1D705}(s)$
is the residue field of
$\unicode[STIX]{x1D705}(s)$
is the residue field of
![]() $s\in \operatorname{Spec}(R)$
. Then, there exists a dense open subset
$s\in \operatorname{Spec}(R)$
. Then, there exists a dense open subset
![]() $U\subseteq \operatorname{Max}\operatorname{Spec}(A)$
such that
$U\subseteq \operatorname{Max}\operatorname{Spec}(A)$
such that
![]() $a_{d}(R)=a_{d}(R_{s})$
for all
$a_{d}(R)=a_{d}(R_{s})$
for all
![]() $s\in U$
.
$s\in U$
.
Proof. Since
![]() $R_{0}$
is a finitely generated graded
$R_{0}$
is a finitely generated graded
![]() $A$
-algebra, we write
$A$
-algebra, we write
![]() $R_{0}\cong B/J$
, for some homogeneous ideal
$R_{0}\cong B/J$
, for some homogeneous ideal
![]() $J\subseteq B:=A[x_{1},\ldots ,x_{n}]$
. Let
$J\subseteq B:=A[x_{1},\ldots ,x_{n}]$
. Let
![]() $T=B\otimes _{A}K\cong K[x_{1},\ldots ,x_{n}]$
, and for
$T=B\otimes _{A}K\cong K[x_{1},\ldots ,x_{n}]$
, and for
![]() $s\in \operatorname{Max}\operatorname{Spec}(R)$
, let
$s\in \operatorname{Max}\operatorname{Spec}(R)$
, let
![]() $B_{s}=B\otimes _{A}\unicode[STIX]{x1D705}(s)\cong \unicode[STIX]{x1D705}(s)[x_{1},\ldots ,x_{n}]$
. By [Reference Hochster and HunekeHH99, Theorem 2.3.5 & Theorem 2.3.15], there exists a dense open subset
$B_{s}=B\otimes _{A}\unicode[STIX]{x1D705}(s)\cong \unicode[STIX]{x1D705}(s)[x_{1},\ldots ,x_{n}]$
. By [Reference Hochster and HunekeHH99, Theorem 2.3.5 & Theorem 2.3.15], there exists a dense open subset
![]() $U\subseteq \operatorname{Max}\operatorname{Spec}(R)$
such that, for all
$U\subseteq \operatorname{Max}\operatorname{Spec}(R)$
such that, for all
![]() $s\in U$
,
$s\in U$
,
![]() $R_{s}$
is Cohen–Macaulay of dimension
$R_{s}$
is Cohen–Macaulay of dimension
![]() $d=\dim (R)$
. Furthermore, the graded Betti numbers of
$d=\dim (R)$
. Furthermore, the graded Betti numbers of
![]() $R$
over
$R$
over
![]() $T$
are the same as the graded Betti numbers of
$T$
are the same as the graded Betti numbers of
![]() $R_{s}$
over
$R_{s}$
over
![]() $B_{s}$
[Reference Hochster and HunekeHH99, Theorem 2.3.5(e)]. In particular, it follows from Remark 6.6 that
$B_{s}$
[Reference Hochster and HunekeHH99, Theorem 2.3.5(e)]. In particular, it follows from Remark 6.6 that
![]() $a_{d}(R)=a_{d}(R_{s})$
for all
$a_{d}(R)=a_{d}(R_{s})$
for all
![]() $s\in U$
.◻
$s\in U$
.◻
Theorem 6.8. Let
![]() $K$
be a field of characteristic zero, and let
$K$
be a field of characteristic zero, and let
![]() $(R,\mathfrak{m},K)$
be a standard graded normal and
$(R,\mathfrak{m},K)$
be a standard graded normal and
![]() $\mathbb{Q}$
-Gorenstein
$\mathbb{Q}$
-Gorenstein
![]() $K$
-algebra such that
$K$
-algebra such that
![]() $X=\operatorname{Spec}R$
is log-terminal. Let
$X=\operatorname{Spec}R$
is log-terminal. Let
![]() $d=\dim (R)$
. Then,
$d=\dim (R)$
. Then,
-
(1)
 $\operatorname{lct}(X)\leqslant -a_{d}(R)$
.
$\operatorname{lct}(X)\leqslant -a_{d}(R)$
. -
(2) If
 $R$
is Gorenstein, then
$R$
is Gorenstein, then
 $\operatorname{lct}(X)=-a_{d}(R).$
$\operatorname{lct}(X)=-a_{d}(R).$
Proof. We can write
![]() $R=K[x_{1},\ldots ,x_{n}]/(f_{1},\ldots ,f_{\ell })$
for some integer
$R=K[x_{1},\ldots ,x_{n}]/(f_{1},\ldots ,f_{\ell })$
for some integer
![]() $n$
and some homogeneous polynomials
$n$
and some homogeneous polynomials
![]() $f_{1},\ldots ,f_{\ell }\in S:=K[x_{1},\ldots ,x_{n}]$
. Let
$f_{1},\ldots ,f_{\ell }\in S:=K[x_{1},\ldots ,x_{n}]$
. Let
![]() $A$
be the finitely generated
$A$
be the finitely generated
![]() $\mathbb{Z}$
-algebra generated by all the coefficients of
$\mathbb{Z}$
-algebra generated by all the coefficients of
![]() $f_{1},\ldots ,f_{\ell }$
. Define
$f_{1},\ldots ,f_{\ell }$
. Define
![]() $T:=A[x_{1},\ldots ,x_{n}]$
and notice that, if we set
$T:=A[x_{1},\ldots ,x_{n}]$
and notice that, if we set
![]() $R_{0}:=T/(f_{1},\ldots ,f_{\ell })$
, we have that
$R_{0}:=T/(f_{1},\ldots ,f_{\ell })$
, we have that
![]() $R_{0}\otimes _{A}K\cong R$
. Since
$R_{0}\otimes _{A}K\cong R$
. Since
![]() $X$
is log-terminal,
$X$
is log-terminal,
![]() $R$
is a Cohen–Macaulay ring. For a closed point
$R$
is a Cohen–Macaulay ring. For a closed point
![]() $s\in \operatorname{Spec}(A)$
, set
$s\in \operatorname{Spec}(A)$
, set
![]() $R_{s}:=R_{0}\otimes _{A}\unicode[STIX]{x1D705}(s)$
, and
$R_{s}:=R_{0}\otimes _{A}\unicode[STIX]{x1D705}(s)$
, and
![]() $\mathfrak{m}_{s}:=(x_{1},\ldots ,x_{n})R_{s}$
. For
$\mathfrak{m}_{s}:=(x_{1},\ldots ,x_{n})R_{s}$
. For
![]() $m\in \mathbb{N}$
, let
$m\in \mathbb{N}$
, let
![]() $\unicode[STIX]{x1D706}_{m}=\operatorname{lct}(X)-1/m$
. Then, the pair
$\unicode[STIX]{x1D706}_{m}=\operatorname{lct}(X)-1/m$
. Then, the pair
![]() $(X,\unicode[STIX]{x1D706}_{m}Y)$
is klt by Remark 6.2. Thus,
$(X,\unicode[STIX]{x1D706}_{m}Y)$
is klt by Remark 6.2. Thus,
![]() $(X,\unicode[STIX]{x1D706}_{m}Y)$
is of dense strongly
$(X,\unicode[STIX]{x1D706}_{m}Y)$
is of dense strongly
![]() $F$
-regular type [Reference Hara and YoshidaHY03, Theorem 6.8] [Reference TakagiTak04, Corollary 3.5]. It follows that
$F$
-regular type [Reference Hara and YoshidaHY03, Theorem 6.8] [Reference TakagiTak04, Corollary 3.5]. It follows that
![]() $(R_{s},\mathfrak{m}_{s}^{\unicode[STIX]{x1D706}_{m}})$
is strongly
$(R_{s},\mathfrak{m}_{s}^{\unicode[STIX]{x1D706}_{m}})$
is strongly
![]() $F$
-regular for each closed point
$F$
-regular for each closed point
![]() $s\in V$
, where
$s\in V$
, where
![]() $V\subseteq \operatorname{Max}\operatorname{Spec}(A)$
is a dense set. By Remark 6.4, we have that
$V\subseteq \operatorname{Max}\operatorname{Spec}(A)$
is a dense set. By Remark 6.4, we have that
![]() $\unicode[STIX]{x1D706}_{m}\leqslant \operatorname{fpt}(R_{s})$
for all
$\unicode[STIX]{x1D706}_{m}\leqslant \operatorname{fpt}(R_{s})$
for all
![]() $m$
, and hence
$m$
, and hence
by Theorem 4.3. By Lemma 6.7, there exists a dense open subset
![]() $U\subseteq \operatorname{Max}\operatorname{Spec}(A)$
such that
$U\subseteq \operatorname{Max}\operatorname{Spec}(A)$
such that
![]() $a_{d}(R_{s})=a_{d}(R)$
for all
$a_{d}(R_{s})=a_{d}(R)$
for all
![]() $s\in U$
. Thus, for
$s\in U$
. Thus, for
![]() $s$
in nonempty intersection
$s$
in nonempty intersection
![]() $U\cap V$
, we have
$U\cap V$
, we have
After taking the limit as
![]() $m\rightarrow \infty$
, we obtain that
$m\rightarrow \infty$
, we obtain that
![]() $\operatorname{lct}(X)\leqslant -a_{d}(R)$
.
$\operatorname{lct}(X)\leqslant -a_{d}(R)$
.
For the second result, we note that if
![]() $R$
is a Gorenstein ring, then
$R$
is a Gorenstein ring, then
![]() $R_{s}$
is a Gorenstein ring for
$R_{s}$
is a Gorenstein ring for
![]() $s$
in a dense open subset
$s$
in a dense open subset
![]() $W\subseteq \operatorname{Max}\operatorname{Spec}(A)$
[Reference Hochster and HunekeHH99, Theorem 2.3.15]. Let
$W\subseteq \operatorname{Max}\operatorname{Spec}(A)$
[Reference Hochster and HunekeHH99, Theorem 2.3.15]. Let
![]() $U$
be as above. Then,
$U$
be as above. Then,
![]() $\operatorname{fpt}(R_{s})=-a_{d}(R_{s})=-a_{d}(R)$
for
$\operatorname{fpt}(R_{s})=-a_{d}(R_{s})=-a_{d}(R)$
for
![]() $s\in W\cap U$
, where
$s\in W\cap U$
, where
![]() $W\cap U$
is a dense open subset of
$W\cap U$
is a dense open subset of
![]() $\operatorname{Max}\operatorname{Spec}(A)$
. Let
$\operatorname{Max}\operatorname{Spec}(A)$
. Let
![]() $\unicode[STIX]{x1D6FF}_{m}:=-a_{d}(R)-1/m$
. Because of the equality obtained above, we have that
$\unicode[STIX]{x1D6FF}_{m}:=-a_{d}(R)-1/m$
. Because of the equality obtained above, we have that
![]() $(R,\mathfrak{m}_{s}^{\unicode[STIX]{x1D6FF}_{m}})$
is
$(R,\mathfrak{m}_{s}^{\unicode[STIX]{x1D6FF}_{m}})$
is
![]() $F$
-pure for
$F$
-pure for
![]() $s\in W$
. Thus,
$s\in W$
. Thus,
![]() $\unicode[STIX]{x1D6FF}_{m}\leqslant \operatorname{lct}(X)$
for every
$\unicode[STIX]{x1D6FF}_{m}\leqslant \operatorname{lct}(X)$
for every
![]() $m\in \mathbb{N}$
[Reference Takagi and WatanabeTW04, Proposition 3.2(1)], and hence
$m\in \mathbb{N}$
[Reference Takagi and WatanabeTW04, Proposition 3.2(1)], and hence
![]() $-a_{d}(R)\leqslant \operatorname{lct}(X)$
. The desired equality now follows from the first part.◻
$-a_{d}(R)\leqslant \operatorname{lct}(X)$
. The desired equality now follows from the first part.◻
A key point in the proof of Theorem 6.8 is that, if
![]() $X$
is log-terminal, then
$X$
is log-terminal, then
and a pair is klt if and only if the pair is of dense strongly
![]() $F$
-regular type. In a private communication with Linquan Ma and Karl Schwede, we were informed that Theorem 6.8 holds, more generally, when
$F$
-regular type. In a private communication with Linquan Ma and Karl Schwede, we were informed that Theorem 6.8 holds, more generally, when
![]() $X$
is a
$X$
is a
![]() $\mathbb{Q}$
-Gorenstein log-canonical normal scheme. The proof involves methods in characteristic zero. Our proof of Theorem 6.8, instead, relies on reduction to positive characteristic techniques. If we try to replace log-terminal by log-canonical in our proof, we face a very important and longstanding open problem in birational geometry, that is, whether a pair is log-canonical if and only if it is of dense
$\mathbb{Q}$
-Gorenstein log-canonical normal scheme. The proof involves methods in characteristic zero. Our proof of Theorem 6.8, instead, relies on reduction to positive characteristic techniques. If we try to replace log-terminal by log-canonical in our proof, we face a very important and longstanding open problem in birational geometry, that is, whether a pair is log-canonical if and only if it is of dense
![]() $F$
-pure type (see [Reference TakagiTak04, Reference Hara and WatanabeHW02, Reference Mustaţă and SrinivasMS11]). To the best of our knowledge, the characteristic zero analogue of Theorem 4.3 is open for non
$F$
-pure type (see [Reference TakagiTak04, Reference Hara and WatanabeHW02, Reference Mustaţă and SrinivasMS11]). To the best of our knowledge, the characteristic zero analogue of Theorem 4.3 is open for non
![]() $\mathbb{Q}$
-Gorenstein rings. We note that in this case one can still define log-canonical singularities by the work of De Fernex and Hacon [Reference de Fernex and HacondFH09]. Then, we ask the following question.
$\mathbb{Q}$
-Gorenstein rings. We note that in this case one can still define log-canonical singularities by the work of De Fernex and Hacon [Reference de Fernex and HacondFH09]. Then, we ask the following question.
Question 6.9. Let
![]() $(R,\mathfrak{m},K)$
be a standard graded normal algebra over a field,
$(R,\mathfrak{m},K)$
be a standard graded normal algebra over a field,
![]() $K$
, of characteristic zero. Let
$K$
, of characteristic zero. Let
![]() $d=\dim (R)$
and let
$d=\dim (R)$
and let
![]() $X=\operatorname{Spec}R$
. Suppose that
$X=\operatorname{Spec}R$
. Suppose that
![]() $X$
is log-canonical. Is
$X$
is log-canonical. Is
![]() $\operatorname{lct}(X)\leqslant -a_{i}(R)$
for every
$\operatorname{lct}(X)\leqslant -a_{i}(R)$
for every
![]() $i\in \mathbb{N}$
?
$i\in \mathbb{N}$
?
Ma also informed us that the analogue of Theorem 5.2 in characteristic zero is also true. This can be proved using geometric methods in characteristic zero, such as Bertini theorems, and his recent work on Du Bois singularities [Reference MaMa15].
7 Homological invariants of
 $F$
-pure rings
$F$
-pure rings
Let
![]() $K$
be a field and let
$K$
be a field and let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring. Let
![]() $I\subseteq S$
be a homogeneous ideal, and let
$I\subseteq S$
be a homogeneous ideal, and let
![]() $R=S/I$
. Suppose that
$R=S/I$
. Suppose that
![]() $I=(f_{1},\ldots ,f_{j})$
is generated by forms of degree
$I=(f_{1},\ldots ,f_{j})$
is generated by forms of degree
![]() $d_{i}=\deg (f_{i})$
. Let
$d_{i}=\deg (f_{i})$
. Let
![]() $G_{\bullet }$
be the minimal graded free resolution of
$G_{\bullet }$
be the minimal graded free resolution of
![]() $R$
. Each
$R$
. Each
![]() $G_{i}$
can be written as a direct sum of copies of
$G_{i}$
can be written as a direct sum of copies of
![]() $S$
with shifts:
$S$
with shifts:
where
![]() $S(-j)$
denotes a rank one free module where the generator has degree
$S(-j)$
denotes a rank one free module where the generator has degree
![]() $j$
. The exponents
$j$
. The exponents
![]() $\unicode[STIX]{x1D6FD}_{i,j}(R)$
are called the graded Betti numbers of
$\unicode[STIX]{x1D6FD}_{i,j}(R)$
are called the graded Betti numbers of
![]() $R$
. We define the projective dimension of
$R$
. We define the projective dimension of
![]() $R$
by
$R$
by
The Castelnuovo–Mumford regularity of
![]() $R=S/I$
is defined by
$R=S/I$
is defined by
Equivalently, if
![]() $d=\dim (R)$
, it can be defined as
$d=\dim (R)$
, it can be defined as
Suppose that
![]() $R$
is an
$R$
is an
![]() $F$
-pure ring. In this section, we provide bounds for the projective dimension and Castelnuovo–Mumford regularity of
$F$
-pure ring. In this section, we provide bounds for the projective dimension and Castelnuovo–Mumford regularity of
![]() $R$
over
$R$
over
![]() $S$
. This relates to an important question in commutative algebra asked by Stillman:
$S$
. This relates to an important question in commutative algebra asked by Stillman:
Question 7.1. [Reference Peeva and StillmanPS09, Problem 3.14]
Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field
![]() $K$
and fix a sequence of natural numbers
$K$
and fix a sequence of natural numbers
![]() $d_{1},\ldots ,d_{j}$
. Does there exist a constant
$d_{1},\ldots ,d_{j}$
. Does there exist a constant
![]() $C=C(d_{1},\ldots ,d_{j})$
(independent of
$C=C(d_{1},\ldots ,d_{j})$
(independent of
![]() $n$
) such that
$n$
) such that
for all homogeneous ideals
![]() $J\subseteq S$
generated by homogeneous polynomials of degrees
$J\subseteq S$
generated by homogeneous polynomials of degrees
![]() $d_{1},\ldots ,d_{j}$
?
$d_{1},\ldots ,d_{j}$
?
Recall that
![]() $b_{\mathfrak{m}}(p^{e})=\max \{r\mid \mathfrak{m}^{r}\not \subseteq I_{e}(R)\}$
. Proposition 5.4 gives a relation between
$b_{\mathfrak{m}}(p^{e})=\max \{r\mid \mathfrak{m}^{r}\not \subseteq I_{e}(R)\}$
. Proposition 5.4 gives a relation between
![]() $b_{\mathfrak{m}}(p)$
and
$b_{\mathfrak{m}}(p)$
and
![]() $\operatorname{depth}_{S}(R)$
, hence between
$\operatorname{depth}_{S}(R)$
, hence between
![]() $b_{\mathfrak{m}}(p)$
and
$b_{\mathfrak{m}}(p)$
and
![]() $\operatorname{pd}_{S}(R)$
by the Auslander–Buchsbaum’s formula. For
$\operatorname{pd}_{S}(R)$
by the Auslander–Buchsbaum’s formula. For
![]() $F$
-pure rings, the projective dimension and the Castelnuovo–Mumford regularity have explicit upper bounds. The bound for the projective dimension easily follows from a special case of a result of Lyubeznik.
$F$
-pure rings, the projective dimension and the Castelnuovo–Mumford regularity have explicit upper bounds. The bound for the projective dimension easily follows from a special case of a result of Lyubeznik.
Theorem 7.2. [Reference LyubeznikLyu06, Corollary 3.2]
Let
![]() $S$
be regular local ring of positive characteristic
$S$
be regular local ring of positive characteristic
![]() $p$
, and let
$p$
, and let
![]() $I\subseteq S$
be an ideal. Let
$I\subseteq S$
be an ideal. Let
![]() $R=S/I$
, with maximal ideal
$R=S/I$
, with maximal ideal
![]() $\mathfrak{m}$
. Then, for
$\mathfrak{m}$
. Then, for
![]() $i\in \mathbb{N}$
, we have
$i\in \mathbb{N}$
, we have
![]() $H_{I}^{n-i}(S)=0$
if and only if
$H_{I}^{n-i}(S)=0$
if and only if
![]() $F^{e}:H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is the zero map for some
$F^{e}:H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is the zero map for some
![]() $e\in \mathbb{N}$
.
$e\in \mathbb{N}$
.
We now exhibit some upper bounds for homological invariants of standard graded
![]() $F$
-pure
$F$
-pure
![]() $K$
-algebras. We note that the argument for projective dimension has already been used, essentially, in [Reference Singh and WaltherSW07, Theorem 4.1]. Moreover, the fact that
$K$
-algebras. We note that the argument for projective dimension has already been used, essentially, in [Reference Singh and WaltherSW07, Theorem 4.1]. Moreover, the fact that
![]() $\operatorname{pd}_{S}(S/I)=\operatorname{cd}(I,S)$
if
$\operatorname{pd}_{S}(S/I)=\operatorname{cd}(I,S)$
if
![]() $S/I$
is
$S/I$
is
![]() $F$
-pure was first pointed out in [Reference Dao, Huneke and SchweigDHS13]. However, the bound for the Castelnuovo–Mumford regularity follows from our results in this article, in particular, from Theorem B.
$F$
-pure was first pointed out in [Reference Dao, Huneke and SchweigDHS13]. However, the bound for the Castelnuovo–Mumford regularity follows from our results in this article, in particular, from Theorem B.
Theorem 7.3. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field of positive characteristic
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field of positive characteristic
![]() $p$
. Let
$p$
. Let
![]() $I\subseteq S$
be a homogeneous ideal such that
$I\subseteq S$
be a homogeneous ideal such that
![]() $R=S/I$
is
$R=S/I$
is
![]() $F$
-pure. Then,
$F$
-pure. Then,
where
![]() $\unicode[STIX]{x1D707}_{S}(I)$
denotes the minimal number of generators of
$\unicode[STIX]{x1D707}_{S}(I)$
denotes the minimal number of generators of
![]() $I$
in
$I$
in
![]() $S$
. If
$S$
. If
![]() $K$
is
$K$
is
![]() $F$
-finite, then
$F$
-finite, then
Proof. Since
![]() $R$
is an
$R$
is an
![]() $F$
-pure ring, so is the localization
$F$
-pure ring, so is the localization
![]() $(R^{\prime },\mathfrak{m}^{\prime }):=(R_{\mathfrak{m}},\mathfrak{m}_{\mathfrak{m}})$
. In fact if
$(R^{\prime },\mathfrak{m}^{\prime }):=(R_{\mathfrak{m}},\mathfrak{m}_{\mathfrak{m}})$
. In fact if
![]() $R\subseteq R^{1/p}$
is pure, then so is
$R\subseteq R^{1/p}$
is pure, then so is
![]() $R_{\mathfrak{m}}\subseteq (R^{1/p})_{\mathfrak{m}}=(R_{\mathfrak{m}})^{1/p}$
. Hence the Frobenius homomorphism acts injectively on the local cohomology modules of
$R_{\mathfrak{m}}\subseteq (R^{1/p})_{\mathfrak{m}}=(R_{\mathfrak{m}})^{1/p}$
. Hence the Frobenius homomorphism acts injectively on the local cohomology modules of
![]() $R^{\prime }$
. In particular, for any integer
$R^{\prime }$
. In particular, for any integer
![]() $i$
and for any
$i$
and for any
![]() $e\in \mathbb{N}$
, we have that
$e\in \mathbb{N}$
, we have that
![]() $F^{e}:H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })\rightarrow H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })$
is the zero map if and only if
$F^{e}:H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })\rightarrow H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })$
is the zero map if and only if
![]() $H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })=0$
. Let
$H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })=0$
. Let
![]() $\mathfrak{n}=(x_{1},\ldots ,x_{n})$
. Since
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
. Since
![]() $I$
is homogeneous, we have that
$I$
is homogeneous, we have that
![]() $H_{I}^{n-i}(S)=0$
if and only if
$H_{I}^{n-i}(S)=0$
if and only if
![]() $H_{I_{\mathfrak{n}}}^{n-i}(S_{\mathfrak{n}})=0$
. By Theorem 7.2, it follows that
$H_{I_{\mathfrak{n}}}^{n-i}(S_{\mathfrak{n}})=0$
. By Theorem 7.2, it follows that
![]() $H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })=0$
for all
$H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })=0$
for all
![]() $n-i>\operatorname{cd}(I,S)$
, and
$n-i>\operatorname{cd}(I,S)$
, and
![]() $H_{\mathfrak{m}^{\prime }}^{n-\operatorname{cd}(I,S)}(R^{\prime })\neq 0$
. Therefore, by the Auslander–Buchsbaum’s formula, we get
$H_{\mathfrak{m}^{\prime }}^{n-\operatorname{cd}(I,S)}(R^{\prime })\neq 0$
. Therefore, by the Auslander–Buchsbaum’s formula, we get
![]() $\operatorname{pd}_{S}(R)=n-\operatorname{depth}_{S_{\mathfrak{n}}}(R^{\prime })=\operatorname{cd}(I,S)$
. Since
$\operatorname{pd}_{S}(R)=n-\operatorname{depth}_{S_{\mathfrak{n}}}(R^{\prime })=\operatorname{cd}(I,S)$
. Since
![]() $\operatorname{cd}(I,S)\leqslant \unicode[STIX]{x1D707}_{S}(I)$
, the first claim follows. For the second claim, let
$\operatorname{cd}(I,S)\leqslant \unicode[STIX]{x1D707}_{S}(I)$
, the first claim follows. For the second claim, let
![]() $d=\dim (R)$
. Then we have that
$d=\dim (R)$
. Then we have that
 $$\begin{eqnarray}\displaystyle \operatorname{reg}_{S}(R) & = & \displaystyle \max \{a_{i}(R)+i\mid i=0,\ldots ,d\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max \{i-\operatorname{fpt}(R)\mid i=0,\ldots ,d\}\nonumber\\ \displaystyle & = & \displaystyle d-\operatorname{fpt}(R),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{reg}_{S}(R) & = & \displaystyle \max \{a_{i}(R)+i\mid i=0,\ldots ,d\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max \{i-\operatorname{fpt}(R)\mid i=0,\ldots ,d\}\nonumber\\ \displaystyle & = & \displaystyle d-\operatorname{fpt}(R),\nonumber\end{eqnarray}$$
where the second line follows from Theorem 4.3. ◻
Remark 7.4. In the notation introduced above, Caviglia proved that finding an upper bound
![]() $C=C(d_{1},\ldots ,d_{j})$
for
$C=C(d_{1},\ldots ,d_{j})$
for
![]() $\operatorname{pd}_{S}(R)$
is equivalent to finding an upper bound
$\operatorname{pd}_{S}(R)$
is equivalent to finding an upper bound
![]() $B=B(d_{1},\ldots ,d_{j})$
for
$B=B(d_{1},\ldots ,d_{j})$
for
![]() $\operatorname{reg}_{S}(R)$
(see [Reference PeevaPee11, Theorem 29.5] and [Reference McCullough and SeceleanuMS13, Theorem 2.4]). The bound for
$\operatorname{reg}_{S}(R)$
(see [Reference PeevaPee11, Theorem 29.5] and [Reference McCullough and SeceleanuMS13, Theorem 2.4]). The bound for
![]() $\operatorname{reg}_{S}(R)$
that we give in Theorem 7.3, a priori, does not give an answer to Stillman’s question. However, the inequality
$\operatorname{reg}_{S}(R)$
that we give in Theorem 7.3, a priori, does not give an answer to Stillman’s question. However, the inequality
![]() $\operatorname{pd}_{S}(R)\leqslant \unicode[STIX]{x1D707}_{S}(I)$
for the projective dimension shows that Stillman’s question has positive answer for
$\operatorname{pd}_{S}(R)\leqslant \unicode[STIX]{x1D707}_{S}(I)$
for the projective dimension shows that Stillman’s question has positive answer for
![]() $F$
-pure rings. In particular, there also exists
$F$
-pure rings. In particular, there also exists
![]() $B=B(d_{1},\ldots ,d_{j})$
such that
$B=B(d_{1},\ldots ,d_{j})$
such that
![]() $\operatorname{reg}_{S}(R)\leqslant B$
.
$\operatorname{reg}_{S}(R)\leqslant B$
.
Motivated by the results in the previous theorem, we ask the following question.
Question 7.5. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field,
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field,
![]() $K$
, of characteristic zero, and let
$K$
, of characteristic zero, and let
![]() $I$
be a homogeneous ideal. Suppose that
$I$
be a homogeneous ideal. Suppose that
![]() $R=S/I$
is a normal, and that
$R=S/I$
is a normal, and that
![]() $X=\operatorname{Spec}R$
is log-canonical. Is it true that
$X=\operatorname{Spec}R$
is log-canonical. Is it true that
We end this section by exhibiting an
![]() $S_{k}$
condition that forces an
$S_{k}$
condition that forces an
![]() $F$
-pure ring to be Cohen–Macaulay.
$F$
-pure ring to be Cohen–Macaulay.
Proposition 7.6. Let
![]() $S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field of positive characteristic
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field of positive characteristic
![]() $p$
. Let
$p$
. Let
![]() $I$
be a homogeneous ideal generated by forms
$I$
be a homogeneous ideal generated by forms
![]() $f_{1},\ldots ,f_{\ell }.$
Let
$f_{1},\ldots ,f_{\ell }.$
Let
![]() $D=\deg (f_{1})+\cdots +\deg (f_{\ell }).$
Suppose that
$D=\deg (f_{1})+\cdots +\deg (f_{\ell }).$
Suppose that
![]() $R=S/I$
is
$R=S/I$
is
![]() $F$
-pure. If
$F$
-pure. If
![]() $R_{Q}$
is Cohen–Macaulay for every prime ideal such
$R_{Q}$
is Cohen–Macaulay for every prime ideal such
![]() $\dim (R_{Q})\leqslant D$
, then
$\dim (R_{Q})\leqslant D$
, then
![]() $R$
is Cohen–Macaulay.
$R$
is Cohen–Macaulay.
Proof. Our proof will be by contradiction. Suppose that
![]() $R$
is not Cohen–Macaulay. Then,
$R$
is not Cohen–Macaulay. Then,
![]() $\operatorname{depth}(R)<\dim (R).$
Let
$\operatorname{depth}(R)<\dim (R).$
Let
![]() $c=\operatorname{cd}(I,S)$
and
$c=\operatorname{cd}(I,S)$
and
![]() $r=\operatorname{depth}_{I}(S).$
We have that
$r=\operatorname{depth}_{I}(S).$
We have that
by Theorem 7.3. Let
![]() $Q\in \operatorname{Ass}_{S}H_{I}^{c}(S)$
. Note that
$Q\in \operatorname{Ass}_{S}H_{I}^{c}(S)$
. Note that
![]() $H_{I}^{c}(S_{Q})\neq 0$
by our choice of
$H_{I}^{c}(S_{Q})\neq 0$
by our choice of
![]() $Q$
, and then
$Q$
, and then
![]() $c=\operatorname{cd}(IS_{Q},S_{Q})$
. In addition,
$c=\operatorname{cd}(IS_{Q},S_{Q})$
. In addition,
![]() $H_{I}^{r}(S_{Q})\neq 0$
because
$H_{I}^{r}(S_{Q})\neq 0$
because
![]() $I\subseteq Q$
. Thus,
$I\subseteq Q$
. Thus,
![]() $r=\operatorname{depth}_{I}(S_{Q})$
. It follows that
$r=\operatorname{depth}_{I}(S_{Q})$
. It follows that
by Theorem 7.3. Thus,
![]() $\dim (R_{Q})\neq \operatorname{depth}(R_{Q})$
, and so
$\dim (R_{Q})\neq \operatorname{depth}(R_{Q})$
, and so
![]() $R_{Q}$
is not Cohen–Macaulay.
$R_{Q}$
is not Cohen–Macaulay.
We have that
![]() $\dim S/Q\geqslant n-D$
[Reference ZhangZha11, Theorem 1], therefore
$\dim S/Q\geqslant n-D$
[Reference ZhangZha11, Theorem 1], therefore
![]() $\dim S_{Q}\leqslant D$
, because regular rings satisfy the dimension formula. In particular,
$\dim S_{Q}\leqslant D$
, because regular rings satisfy the dimension formula. In particular,
![]() $\dim (R_{Q})\leqslant D$
. Since we are assuming that
$\dim (R_{Q})\leqslant D$
. Since we are assuming that
![]() $R$
is
$R$
is
![]() $S_{D}$
, we have that
$S_{D}$
, we have that
![]() $R_{Q}$
must be Cohen–Macaulay, and we reach a contradiction.◻
$R_{Q}$
must be Cohen–Macaulay, and we reach a contradiction.◻
Acknowledgments
We thank Craig Huneke for very helpful discussions. In particular, we thank him for suggesting a shorter and more elegant proof of Theorem 5.2. We thank Karl Schwede for discussions about geometric interpretations of Theorem 5.8, and Linquan Ma for helpful comments about Section 6. We also thank Andrew Bydlon for reading a preliminary version of this article, and for useful feedback and comments. We thank the referee for carefully reading the article, and for suggesting improvements to the exposition.