We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A classical result due to Paley and Wiener characterizes the existence of a nonzero function in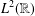 
$L^{2}(\mathbb{R})$, supported on a half-line, in terms of the decay of its Fourier transform. In this paper, we prove an analogue of this result for Damek–Ricci spaces.
