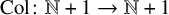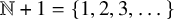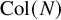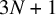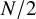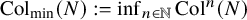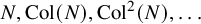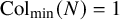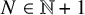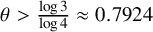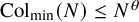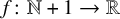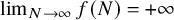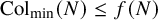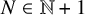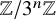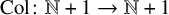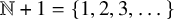Define the Collatz map ${\operatorname {Col}} \colon \mathbb {N}+1 \to \mathbb {N}+1$ on the positive integers $\mathbb {N}+1 = \{1,2,3,\dots \}$ by setting 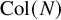${\operatorname {Col}}(N)$ equal to 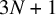$3N+1$ when N is odd and 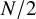$N/2$ when N is even, and let 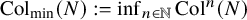${\operatorname {Col}}_{\min }(N) := \inf _{n \in \mathbb {N}} {\operatorname {Col}}^n(N)$ denote the minimal element of the Collatz orbit 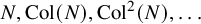$N, {\operatorname {Col}}(N), {\operatorname {Col}}^2(N), \dots $ . The infamous Collatz conjecture asserts that 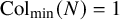${\operatorname {Col}}_{\min }(N)=1$ for all 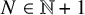$N \in \mathbb {N}+1$ . Previously, it was shown by Korec that for any 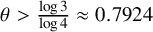$\theta> \frac {\log 3}{\log 4} \approx 0.7924$ , one has 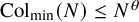${\operatorname {Col}}_{\min }(N) \leq N^\theta $ for almost all $N \in \mathbb {N}+1$ (in the sense of natural density). 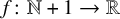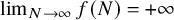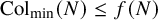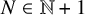In this paper, we show that for any function $f \colon \mathbb {N}+1 \to \mathbb {R}$ with $\lim _{N \to \infty } f(N)=+\infty $ , one has ${\operatorname {Col}}_{\min }(N) \leq f(N)$ for almost all $N \in \mathbb {N}+1$ (in the sense of logarithmic density). 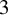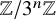Our proof proceeds by establishing a stabilisation property for a certain first passage random variable associated with the Collatz iteration (or more precisely, the closely related Syracuse iteration), which in turn follows from estimation of the characteristic function of a certain skew random walk on a $3$ -adic cyclic group $\mathbb {Z}/3^n\mathbb {Z}$ at high frequencies. This estimation is achieved by studying how a certain two-dimensional renewal process interacts with a union of triangles associated to a given frequency.