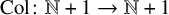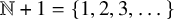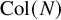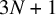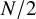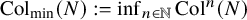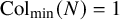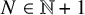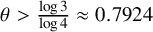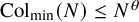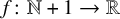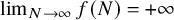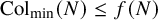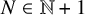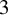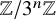1 Introduction
1.1 Statement of main result
Let
![]() $\mathbb {N} := \{0,1,2,\dots \}$
denote the natural numbers, so that
$\mathbb {N} := \{0,1,2,\dots \}$
denote the natural numbers, so that
![]() $\mathbb {N}+1 = \{1,2,3,\dots \}$
are the positive integers. The Collatz map
$\mathbb {N}+1 = \{1,2,3,\dots \}$
are the positive integers. The Collatz map
![]() ${\operatorname {Col}} \colon \mathbb {N}+1 \to \mathbb {N}+1$
is defined by setting
${\operatorname {Col}} \colon \mathbb {N}+1 \to \mathbb {N}+1$
is defined by setting
![]() ${\operatorname {Col}}(N) := 3N+1$
when N is odd and
${\operatorname {Col}}(N) := 3N+1$
when N is odd and
![]() ${\operatorname {Col}}(N) := N/2$
when N is even. For any
${\operatorname {Col}}(N) := N/2$
when N is even. For any
![]() $N \in \mathbb {N}+1$
, let
$N \in \mathbb {N}+1$
, let
![]() ${\operatorname {Col}}_{\min }(N) := \min {\operatorname {Col}}^{\mathbb {N}}(N) = \inf _{n \in \mathbb {N}} {\operatorname {Col}}^n(N)$
denote the minimal element of the Collatz orbit
${\operatorname {Col}}_{\min }(N) := \min {\operatorname {Col}}^{\mathbb {N}}(N) = \inf _{n \in \mathbb {N}} {\operatorname {Col}}^n(N)$
denote the minimal element of the Collatz orbit
![]() ${\operatorname {Col}}^{\mathbb {N}}(N) := \{ N, {\operatorname {Col}}(N), {\operatorname {Col}}^2(N), \dots \}$
. We have the infamous Collatz conjecture (also known as the
${\operatorname {Col}}^{\mathbb {N}}(N) := \{ N, {\operatorname {Col}}(N), {\operatorname {Col}}^2(N), \dots \}$
. We have the infamous Collatz conjecture (also known as the
![]() $3x+1$
conjecture):
$3x+1$
conjecture):
Conjecture 1.1 (Collatz conjecture)
We have
![]() ${\operatorname {Col}}_{\min }(N)=1$
for all
${\operatorname {Col}}_{\min }(N)=1$
for all
![]() $N \in \mathbb {N}+1$
.
$N \in \mathbb {N}+1$
.
We refer the reader to [Reference Lagarias14], [Reference Chamberland6] for extensive surveys and historical discussion of this conjecture.
While the full resolution of Conjecture 1.1 remains well beyond the reach of current methods, some partial results are known. Numerical computation has verified
![]() ${\operatorname {Col}}_{\min }(N)=1$
for all
${\operatorname {Col}}_{\min }(N)=1$
for all
![]() $N \leq 5.78 \times 10^{18}$
[Reference Oliveira e Silva17], for all
$N \leq 5.78 \times 10^{18}$
[Reference Oliveira e Silva17], for all
![]() $N \leq 10^{20}$
[Reference Roosendaal18], and most recently for all
$N \leq 10^{20}$
[Reference Roosendaal18], and most recently for all
![]() $N \leq 2^{68} \approx 2.95 \times 10^{20}$
[Reference Barina3], while Krasikov and Lagarias [Reference Krasikov and Lagarias13] showed that
$N \leq 2^{68} \approx 2.95 \times 10^{20}$
[Reference Barina3], while Krasikov and Lagarias [Reference Krasikov and Lagarias13] showed that
for all sufficiently large x, where
![]() $\# E$
denotes the cardinality of a finite set E, and our conventions for asymptotic notation are set out in Section 2. In this paper, we will focus on a different type of partial result, in which one establishes upper bounds on the minimal orbit value
$\# E$
denotes the cardinality of a finite set E, and our conventions for asymptotic notation are set out in Section 2. In this paper, we will focus on a different type of partial result, in which one establishes upper bounds on the minimal orbit value
![]() ${\operatorname {Col}}_{\min }(N)$
for ‘almost all’
${\operatorname {Col}}_{\min }(N)$
for ‘almost all’
![]() $N \in \mathbb {N}+1$
. For technical reasons, the notion of ‘almost all’ that we will use here is based on logarithmic density, which has better approximate multiplicative invariance properties than the more familiar notion of natural density (see [Reference Tao20] for a related phenomenon in a more number-theoretic context). Due to the highly probabilistic nature of the arguments in this paper, we will define logarithmic density using the language of probability theory.
$N \in \mathbb {N}+1$
. For technical reasons, the notion of ‘almost all’ that we will use here is based on logarithmic density, which has better approximate multiplicative invariance properties than the more familiar notion of natural density (see [Reference Tao20] for a related phenomenon in a more number-theoretic context). Due to the highly probabilistic nature of the arguments in this paper, we will define logarithmic density using the language of probability theory.
Definition 1.2 (Almost all)
Given a finite non-empty subset R of
![]() $\mathbb {N}+1$
, we defineFootnote
1
$\mathbb {N}+1$
, we defineFootnote
1
![]() $\mathbf {Log}(R)$
to be a random variable taking values in R with the logarithmically uniform distribution
$\mathbf {Log}(R)$
to be a random variable taking values in R with the logarithmically uniform distribution
 $$ \begin{align*}\mathbb{P}( \mathbf{Log}(R) \in A ) = \frac{\sum_{N \in A \cap R} \frac{1}{N}}{\sum_{N \in R} \frac{1}{N}}\end{align*} $$
$$ \begin{align*}\mathbb{P}( \mathbf{Log}(R) \in A ) = \frac{\sum_{N \in A \cap R} \frac{1}{N}}{\sum_{N \in R} \frac{1}{N}}\end{align*} $$
for all
![]() $A \subset \mathbb {N}+1$
. The logarithmic density of a set
$A \subset \mathbb {N}+1$
. The logarithmic density of a set
![]() $A \subset \mathbb {N}+1$
is then defined to be
$A \subset \mathbb {N}+1$
is then defined to be
![]() $\lim _{x \to \infty } \mathbb {P}( \mathbf {Log}(\mathbb {N}+1 \cap [1,x]) \in A )$
, provided that the limit exists. We say that a property
$\lim _{x \to \infty } \mathbb {P}( \mathbf {Log}(\mathbb {N}+1 \cap [1,x]) \in A )$
, provided that the limit exists. We say that a property
![]() $P(N)$
holds for almost all
$P(N)$
holds for almost all
![]() $N \in \mathbb {N}+1$
if
$N \in \mathbb {N}+1$
if
![]() $P(N)$
holds for N in a subset of
$P(N)$
holds for N in a subset of
![]() $\mathbb {N}+1$
of logarithmic density
$\mathbb {N}+1$
of logarithmic density
![]() $1$
, or equivalently if
$1$
, or equivalently if
In Terras [Reference Terras21] (and independently Everett [Reference Everett8]), it was shown that
![]() ${\operatorname {Col}}_{\min }(N) < N$
for almost all N. This was improved by Allouche [Reference Allouche1] to
${\operatorname {Col}}_{\min }(N) < N$
for almost all N. This was improved by Allouche [Reference Allouche1] to
![]() ${\operatorname {Col}}_{\min }(N) < N^\theta $
for almost all N, and any fixed constant
${\operatorname {Col}}_{\min }(N) < N^\theta $
for almost all N, and any fixed constant
![]() $\theta>\frac {3}{2} - \frac {\log 3}{\log 2} \approx 0.869$
; the range of
$\theta>\frac {3}{2} - \frac {\log 3}{\log 2} \approx 0.869$
; the range of
![]() $\theta $
was later extended to
$\theta $
was later extended to
![]() $\theta> \frac {\log 3}{\log 4} \approx 0.7924$
by Korec [Reference Korec9]. (Indeed, in these results one can use natural density instead of logarithmic density to define ‘almost all’.) It is tempting to try to iterate these results to lower the value of
$\theta> \frac {\log 3}{\log 4} \approx 0.7924$
by Korec [Reference Korec9]. (Indeed, in these results one can use natural density instead of logarithmic density to define ‘almost all’.) It is tempting to try to iterate these results to lower the value of
![]() $\theta $
further. However, one runs into the difficulty that the uniform (or logarithmic) measure does not enjoy any invariance properties with respect to the Collatz map: in particular, even if it is true that
$\theta $
further. However, one runs into the difficulty that the uniform (or logarithmic) measure does not enjoy any invariance properties with respect to the Collatz map: in particular, even if it is true that
![]() ${\operatorname {Col}}_{\min }(N) < x^\theta $
for almost all
${\operatorname {Col}}_{\min }(N) < x^\theta $
for almost all
![]() $N \in [1,x]$
, and
$N \in [1,x]$
, and
![]() ${\operatorname {Col}}_{\min }(N') \leq x^{\theta ^2}$
for almost all
${\operatorname {Col}}_{\min }(N') \leq x^{\theta ^2}$
for almost all
![]() $N' \in [1, x^\theta ]$
, the two claims cannot be immediately concatenated to imply that
$N' \in [1, x^\theta ]$
, the two claims cannot be immediately concatenated to imply that
![]() ${\operatorname {Col}}_{\min }(N) \leq x^{\theta ^2}$
for almost all
${\operatorname {Col}}_{\min }(N) \leq x^{\theta ^2}$
for almost all
![]() $N \in [1,x]$
, since the Collatz iteration may send almost all of
$N \in [1,x]$
, since the Collatz iteration may send almost all of
![]() $[1,x]$
into a very sparse subset of
$[1,x]$
into a very sparse subset of
![]() $[1,x^\theta ]$
, and in particular into the exceptional set of the latter claim
$[1,x^\theta ]$
, and in particular into the exceptional set of the latter claim
![]() ${\operatorname {Col}}_{\min }(N') \leq x^{\theta ^2}$
.
${\operatorname {Col}}_{\min }(N') \leq x^{\theta ^2}$
.
Nevertheless, in this paper, we show that it is possible to locate an alternate probability measure (or, more precisely, a family of probability measures) on the natural numbers with enough invariance properties that an iterative argument does become fruitful. More precisely, the main result of this paper is the following improvement of these ‘almost all’ results.
Theorem 1.3 (Almost all Collatz orbits attain almost bounded values)
Let
![]() $f \colon \mathbb {N} + 1 \to \mathbb {R}$
be any function with
$f \colon \mathbb {N} + 1 \to \mathbb {R}$
be any function with
![]() $\lim _{N \to \infty } f(N) = +\infty $
. Then one has
$\lim _{N \to \infty } f(N) = +\infty $
. Then one has
![]() ${\operatorname {Col}}_{\min }(N) < f(N)$
for almost all
${\operatorname {Col}}_{\min }(N) < f(N)$
for almost all
![]() $N \in \mathbb {N}+1$
(in the sense of logarithmic density).
$N \in \mathbb {N}+1$
(in the sense of logarithmic density).
Thus, for instance, one has
![]() ${\operatorname {Col}}_{\min }(N) < \log \log \log \log N$
for almost all N.
${\operatorname {Col}}_{\min }(N) < \log \log \log \log N$
for almost all N.
Remark 1.4. One could ask whether it is possible to sharpen the conclusion of Theorem 1.3 further, to assert that there is an absolute constant
![]() $C_0$
such that
$C_0$
such that
![]() ${\operatorname {Col}}_{\min }(N) \leq C_0$
for almost all
${\operatorname {Col}}_{\min }(N) \leq C_0$
for almost all
![]() $N \in \mathbb {N}+1$
. However, this question is likely to be almost as hard to settle as the full Collatz conjecture and out of reach of the methods of this paper. Indeed, suppose for any given
$N \in \mathbb {N}+1$
. However, this question is likely to be almost as hard to settle as the full Collatz conjecture and out of reach of the methods of this paper. Indeed, suppose for any given
![]() $C_0$
that there existed an orbit
$C_0$
that there existed an orbit
![]() ${\operatorname {Col}}^{\mathbb {N}}(N_0) = \{N_0, {\operatorname {Col}}(N_0), {\operatorname {Col}}^2(N_0),\dots \}$
that never dropped below
${\operatorname {Col}}^{\mathbb {N}}(N_0) = \{N_0, {\operatorname {Col}}(N_0), {\operatorname {Col}}^2(N_0),\dots \}$
that never dropped below
![]() $C_0$
(this is the case if there are infinitely many periodic orbits, or if there is at least one unbounded orbit). Then probabilistic heuristics (such as equation (1.16) below) suggest that for a positive density set of
$C_0$
(this is the case if there are infinitely many periodic orbits, or if there is at least one unbounded orbit). Then probabilistic heuristics (such as equation (1.16) below) suggest that for a positive density set of
![]() $N \in \mathbb {N}+1$
, the orbit
$N \in \mathbb {N}+1$
, the orbit
![]() ${\operatorname {Col}}^{\mathbb {N}}(N) = \{N, {\operatorname {Col}}(N), {\operatorname {Col}}^2(N), \dots \}$
should encounter one of the elements
${\operatorname {Col}}^{\mathbb {N}}(N) = \{N, {\operatorname {Col}}(N), {\operatorname {Col}}^2(N), \dots \}$
should encounter one of the elements
![]() ${\operatorname {Col}}^n(N_0)$
of the orbit of
${\operatorname {Col}}^n(N_0)$
of the orbit of
![]() $N_0$
before going below
$N_0$
before going below
![]() $C_0$
, and then the orbit of N will never dip below
$C_0$
, and then the orbit of N will never dip below
![]() $C_0$
. However, Theorem 1.3 is easily seenFootnote
2
to be equivalent to the assertion that for any
$C_0$
. However, Theorem 1.3 is easily seenFootnote
2
to be equivalent to the assertion that for any
![]() $\delta>0$
, there exists a constant
$\delta>0$
, there exists a constant
![]() $C_\delta $
such that
$C_\delta $
such that
![]() ${\operatorname {Col}}_{\min }(N) \leq C_\delta $
for all N in a subset of
${\operatorname {Col}}_{\min }(N) \leq C_\delta $
for all N in a subset of
![]() $\mathbb {N}+1$
of lower logarithmic density (in which the limit in the definition of logarithmic density is replaced by the limit inferior) at least
$\mathbb {N}+1$
of lower logarithmic density (in which the limit in the definition of logarithmic density is replaced by the limit inferior) at least
![]() $1-\delta $
; in fact, (see Theorem 3.1), our arguments give a constant of the form
$1-\delta $
; in fact, (see Theorem 3.1), our arguments give a constant of the form
![]() $C_\delta \ll \exp (\delta ^{-O(1)})$
, and it may be possible to refine the subset so that the logarithmic density (as opposed to merely the lower logarithmic density) exists and is at least
$C_\delta \ll \exp (\delta ^{-O(1)})$
, and it may be possible to refine the subset so that the logarithmic density (as opposed to merely the lower logarithmic density) exists and is at least
![]() $1-\delta $
. In particular,Footnote
3
it is possible in principle that a sufficiently explicit version of the arguments here, when combined with numerical verification of the Collatz conjecture, can be used to show that the Collatz conjecture holds for a set of N of positive logarithmic density. Also, it is plausible that some refinement of the arguments below will allow one to replace logarithmic density with natural density in the definition of ‘almost all’.
$1-\delta $
. In particular,Footnote
3
it is possible in principle that a sufficiently explicit version of the arguments here, when combined with numerical verification of the Collatz conjecture, can be used to show that the Collatz conjecture holds for a set of N of positive logarithmic density. Also, it is plausible that some refinement of the arguments below will allow one to replace logarithmic density with natural density in the definition of ‘almost all’.
1.2 Syracuse formulation
We now discuss the methods of proof of Theorem 1.3. It is convenient to replace the Collatz map
![]() ${\operatorname {Col}} \colon \mathbb {N}+1 \to \mathbb {N}+1$
with a slightly more tractable acceleration
${\operatorname {Col}} \colon \mathbb {N}+1 \to \mathbb {N}+1$
with a slightly more tractable acceleration
![]() $N \mapsto {\operatorname {Col}}^{f(N)}(N)$
of that map. One common instance of such an acceleration in the literature is the map
$N \mapsto {\operatorname {Col}}^{f(N)}(N)$
of that map. One common instance of such an acceleration in the literature is the map
![]() ${\operatorname {Col}}_2 \colon \mathbb {N}+1 \to \mathbb {N}+1$
, defined by setting
${\operatorname {Col}}_2 \colon \mathbb {N}+1 \to \mathbb {N}+1$
, defined by setting
![]() ${\operatorname {Col}}_2(N) := {\operatorname {Col}}^2(N) = \frac {3N+1}{2}$
when N is odd and
${\operatorname {Col}}_2(N) := {\operatorname {Col}}^2(N) = \frac {3N+1}{2}$
when N is odd and
![]() ${\operatorname {Col}}_2(N) := \frac {N}{2}$
when N is even. Each iterate of the map
${\operatorname {Col}}_2(N) := \frac {N}{2}$
when N is even. Each iterate of the map
![]() ${\operatorname {Col}}_2$
performs exactly one division by
${\operatorname {Col}}_2$
performs exactly one division by
![]() $2$
, and for this reason
$2$
, and for this reason
![]() ${\operatorname {Col}}_2$
is a particularly convenient choice of map when performing ‘
${\operatorname {Col}}_2$
is a particularly convenient choice of map when performing ‘
![]() $2$
-adic’ analysis of the Collatz iteration. It is easy to see that
$2$
-adic’ analysis of the Collatz iteration. It is easy to see that
![]() ${\operatorname {Col}}_{\min }(N) = ({\operatorname {Col}}_2)_{\min }(N)$
for all
${\operatorname {Col}}_{\min }(N) = ({\operatorname {Col}}_2)_{\min }(N)$
for all
![]() $N \in \mathbb {N}+1$
, so all the results in this paper concerning
$N \in \mathbb {N}+1$
, so all the results in this paper concerning
![]() ${\operatorname {Col}}$
may be equivalently reformulated using
${\operatorname {Col}}$
may be equivalently reformulated using
![]() ${\operatorname {Col}}_2$
. The triple iterate
${\operatorname {Col}}_2$
. The triple iterate
![]() ${\operatorname {Col}}^3$
was also recently proposed as an acceleration in [Reference Carletti and Fanelli5]. However, the methods in this paper will rely instead on ‘
${\operatorname {Col}}^3$
was also recently proposed as an acceleration in [Reference Carletti and Fanelli5]. However, the methods in this paper will rely instead on ‘
![]() $3$
-adic’ analysis, and it will be preferable to use an acceleration of the Collatz map (first appearing to the author’s knowledge in [Reference Crandall7]), which performs exactly one multiplication by
$3$
-adic’ analysis, and it will be preferable to use an acceleration of the Collatz map (first appearing to the author’s knowledge in [Reference Crandall7]), which performs exactly one multiplication by
![]() $3$
per iteration. More precisely, let
$3$
per iteration. More precisely, let
![]() $2\mathbb {N}+1 = \{1,3,5,\dots \}$
denote the odd natural numbers, and define the Syracuse map
$2\mathbb {N}+1 = \{1,3,5,\dots \}$
denote the odd natural numbers, and define the Syracuse map
![]() ${\operatorname {Syr}} \colon 2\mathbb {N}+1 \to 2\mathbb {N}+1$
(OEIS A075677) to be the largest odd number dividing
${\operatorname {Syr}} \colon 2\mathbb {N}+1 \to 2\mathbb {N}+1$
(OEIS A075677) to be the largest odd number dividing
![]() $3N+1$
; thus, for instance,
$3N+1$
; thus, for instance,
Equivalently, one can write
where for each positive integer
![]() $a \in \mathbb {N}+1$
,
$a \in \mathbb {N}+1$
,
![]() ${\operatorname {Aff}}_a\colon \mathbb {R} \to \mathbb {R}$
denotes the affine map
${\operatorname {Aff}}_a\colon \mathbb {R} \to \mathbb {R}$
denotes the affine map
and for each integer M and each prime p, the p-valuation
![]() $\nu _p(M)$
of M is defined as the largest natural number a such that
$\nu _p(M)$
of M is defined as the largest natural number a such that
![]() $p^a$
divides M (with the convention
$p^a$
divides M (with the convention
![]() $\nu _p(0) = +\infty $
). (Note that
$\nu _p(0) = +\infty $
). (Note that
![]() $\nu _2(3N+1)$
is always a positive integer when N is odd.) For any
$\nu _2(3N+1)$
is always a positive integer when N is odd.) For any
![]() $N \in 2\mathbb {N}+1$
, let
$N \in 2\mathbb {N}+1$
, let
![]() ${\operatorname {Syr}}_{\min }(N) := \min {\operatorname {Syr}}^{\mathbb {N}}(N)$
be the minimal element of the Syracuse orbit
${\operatorname {Syr}}_{\min }(N) := \min {\operatorname {Syr}}^{\mathbb {N}}(N)$
be the minimal element of the Syracuse orbit
This Syracuse orbit
![]() ${\operatorname {Syr}}^{\mathbb {N}}(N)$
is nothing more than the odd elements of the corresponding Collatz orbit
${\operatorname {Syr}}^{\mathbb {N}}(N)$
is nothing more than the odd elements of the corresponding Collatz orbit
![]() ${\operatorname {Col}}^{\mathbb {N}}(N)$
, and from this observation it is easy to verify the identity
${\operatorname {Col}}^{\mathbb {N}}(N)$
, and from this observation it is easy to verify the identity
for any
![]() $N \in \mathbb {N}+1$
. Thus, the Collatz conjecture can be equivalently rephrased as
$N \in \mathbb {N}+1$
. Thus, the Collatz conjecture can be equivalently rephrased as
Conjecture 1.5 (Collatz conjecture, Syracuse formulation)
We have
![]() ${\operatorname {Syr}}_{\min }(N)=1$
for all
${\operatorname {Syr}}_{\min }(N)=1$
for all
![]() $N \in 2\mathbb {N}+1$
.
$N \in 2\mathbb {N}+1$
.
We may similarly reformulate Theorem 1.3 in terms of the Syracuse map. We say that a property
![]() $P(N)$
holds for almost all
$P(N)$
holds for almost all
![]() $N \in 2\mathbb {N}+1$
if
$N \in 2\mathbb {N}+1$
if
or equivalently if
![]() $P(N)$
holds for a set of odd natural numbers of logarithmic density
$P(N)$
holds for a set of odd natural numbers of logarithmic density
![]() $1/2$
. Theorem 1.3 is then equivalent to
$1/2$
. Theorem 1.3 is then equivalent to
Theorem 1.6 (Almost all Syracuse orbits attain almost bounded values)
Let
![]() $f\colon 2\mathbb {N} + 1 \to \mathbb {R}$
be a function with
$f\colon 2\mathbb {N} + 1 \to \mathbb {R}$
be a function with
![]() $\lim _{N \to \infty } f(N) = +\infty $
. Then one has
$\lim _{N \to \infty } f(N) = +\infty $
. Then one has
![]() ${\operatorname {Syr}}_{\min }(N) < f(N)$
for almost all
${\operatorname {Syr}}_{\min }(N) < f(N)$
for almost all
![]() $N \in 2\mathbb {N}+1$
.
$N \in 2\mathbb {N}+1$
.
Indeed, if Theorem 1.6 holds and
![]() $f\colon \mathbb {N} +1 \to \mathbb {R}$
is such that
$f\colon \mathbb {N} +1 \to \mathbb {R}$
is such that
![]() $\lim _{N \to \infty } f(N) = +\infty $
, then from equation (1.2), we see that for any
$\lim _{N \to \infty } f(N) = +\infty $
, then from equation (1.2), we see that for any
![]() $a \in \mathbb {N}$
, the set of
$a \in \mathbb {N}$
, the set of
![]() $N \in \mathbb {N}+1$
with
$N \in \mathbb {N}+1$
with
![]() $\nu _2(N) = a$
and
$\nu _2(N) = a$
and
![]() ${\operatorname {Col}}_{\min }( N ) = {\operatorname {Syr}}_{\min }(N/2^a) < f(N)$
has logarithmic density
${\operatorname {Col}}_{\min }( N ) = {\operatorname {Syr}}_{\min }(N/2^a) < f(N)$
has logarithmic density
![]() $2^{-a}$
. Summing over any finite range
$2^{-a}$
. Summing over any finite range
![]() $0 \leq a \leq a_0$
, we obtain a set of logarithmic density
$0 \leq a \leq a_0$
, we obtain a set of logarithmic density
![]() $1 - 2^{-a_0}$
on which the claim
$1 - 2^{-a_0}$
on which the claim
![]() ${\operatorname {Col}}_{\min }(N) < f(N)$
holds, and on sending
${\operatorname {Col}}_{\min }(N) < f(N)$
holds, and on sending
![]() $a_0$
to infinity one obtains Theorem 1.3. The converse implication (which we will not need) is also straightforward and left to the reader.
$a_0$
to infinity one obtains Theorem 1.3. The converse implication (which we will not need) is also straightforward and left to the reader.
The iterates
![]() ${\operatorname {Syr}}^n$
of the Syracuse map can be described explicitly as follows. For any finite tuple
${\operatorname {Syr}}^n$
of the Syracuse map can be described explicitly as follows. For any finite tuple
![]() $\vec a = (a_1,\dots ,a_n) \in (\mathbb {N}+1)^n$
of positive integers, we define the composition
$\vec a = (a_1,\dots ,a_n) \in (\mathbb {N}+1)^n$
of positive integers, we define the composition
![]() ${\operatorname {Aff}}_{\vec a} = {\operatorname {Aff}}_{a_1,\dots ,a_n}\colon \mathbb {R} \to \mathbb {R}$
to be the affine map
${\operatorname {Aff}}_{\vec a} = {\operatorname {Aff}}_{a_1,\dots ,a_n}\colon \mathbb {R} \to \mathbb {R}$
to be the affine map
A brief calculation shows that
where the size
![]() $|\vec a|$
of a tuple
$|\vec a|$
of a tuple
![]() $\vec a$
is defined as
$\vec a$
is defined as
and we define the n-Syracuse offset map
![]() $F_n\colon (\mathbb {N}+1)^n \to \mathbb {Z}[\frac {1}{2}]$
to be the function
$F_n\colon (\mathbb {N}+1)^n \to \mathbb {Z}[\frac {1}{2}]$
to be the function
 $$ \begin{align} F_n(\vec a) &:= \sum_{m=1}^n 3^{n-m} 2^{-a_{[m,n]}} \nonumber\\ &= 3^{n-1} 2^{-a_{[1,n]}} + 3^{n-2} 2^{-a_{[2,n]}} + \dots + 3^1 2^{-a_{[n-1,n]}} + 2^{-a_n}, \end{align} $$
$$ \begin{align} F_n(\vec a) &:= \sum_{m=1}^n 3^{n-m} 2^{-a_{[m,n]}} \nonumber\\ &= 3^{n-1} 2^{-a_{[1,n]}} + 3^{n-2} 2^{-a_{[2,n]}} + \dots + 3^1 2^{-a_{[n-1,n]}} + 2^{-a_n}, \end{align} $$
where we adopt the summation notation
 $$ \begin{align} a_{[j,k]} := \sum_{i=j}^k a_i \end{align} $$
$$ \begin{align} a_{[j,k]} := \sum_{i=j}^k a_i \end{align} $$
for any
![]() $1 \leq j \leq k \leq n$
; thus, for instance,
$1 \leq j \leq k \leq n$
; thus, for instance,
![]() $|\vec a| = a_{[1,n]}$
. The n-Syracuse offset map
$|\vec a| = a_{[1,n]}$
. The n-Syracuse offset map
![]() $F_n$
takes values in the ring
$F_n$
takes values in the ring
![]() $\mathbb {Z}[\frac {1}{2}] := \{ \frac {M}{2^a}: M \in \mathbb {Z}, a \in \mathbb {N} \}$
formed by adjoining
$\mathbb {Z}[\frac {1}{2}] := \{ \frac {M}{2^a}: M \in \mathbb {Z}, a \in \mathbb {N} \}$
formed by adjoining
![]() $\frac {1}{2}$
to the integers.
$\frac {1}{2}$
to the integers.
By iterating equation (1.1) and then using equation (1.3), we conclude that
for any
![]() $N \in 2\mathbb {N}+1$
and
$N \in 2\mathbb {N}+1$
and
![]() $n \in \mathbb {N}$
, where we define n-Syracuse valuation
$n \in \mathbb {N}$
, where we define n-Syracuse valuation
![]() $\vec a^{(n)}(N) \in (\mathbb {N}+1)^n$
of N to be the tuple
$\vec a^{(n)}(N) \in (\mathbb {N}+1)^n$
of N to be the tuple
This tuple is referred to as the n-path of N in [Reference Kontorovich and Sinai12].
The identity in equation (1.7) asserts that
![]() ${\operatorname {Syr}}^n(N)$
is the image of N under a certain affine map
${\operatorname {Syr}}^n(N)$
is the image of N under a certain affine map
![]() ${\operatorname {Aff}}_{\vec a^{(n)}(N)}$
that is determined by the n-Syracuse valuation
${\operatorname {Aff}}_{\vec a^{(n)}(N)}$
that is determined by the n-Syracuse valuation
![]() $\vec a^{(n)}(N)$
of N. This suggests that in order to understand the behaviour of the iterates
$\vec a^{(n)}(N)$
of N. This suggests that in order to understand the behaviour of the iterates
![]() ${\operatorname {Syr}}^n(N)$
of a typical large number N, one needs to understand the behaviour of n-Syracuse valuation
${\operatorname {Syr}}^n(N)$
of a typical large number N, one needs to understand the behaviour of n-Syracuse valuation
![]() $\vec a^{(n)}(N)$
, as well as the n-Syracuse offset map
$\vec a^{(n)}(N)$
, as well as the n-Syracuse offset map
![]() $F_n$
. For the former, we can gain heuristic insight by observing that for a positive integer a, the set of odd natural numbers
$F_n$
. For the former, we can gain heuristic insight by observing that for a positive integer a, the set of odd natural numbers
![]() $N \in 2\mathbb {N}+1$
with
$N \in 2\mathbb {N}+1$
with
![]() $\nu _2(3N+1)=a$
has (logarithmic) relative density
$\nu _2(3N+1)=a$
has (logarithmic) relative density
![]() $2^{-a}$
. To model this probabilistically, we introduce the following probability distribution:
$2^{-a}$
. To model this probabilistically, we introduce the following probability distribution:
Definition 1.7 (Geometric random variable)
If
![]() $\mu> 1$
, we use
$\mu> 1$
, we use
![]() $\mathbf {Geom}(\mu )$
to denote a geometric random variable of mean
$\mathbf {Geom}(\mu )$
to denote a geometric random variable of mean
![]() $\mu $
, that is to say
$\mu $
, that is to say
![]() $\mathbf {Geom}(\mu )$
takes values in
$\mathbf {Geom}(\mu )$
takes values in
![]() $\mathbb {N}+1$
with
$\mathbb {N}+1$
with
 $$ \begin{align*}\mathbb{P}( \mathbf{Geom}(\mu) = a ) = \frac{1}{\mu} \left( \frac{\mu-1}{\mu} \right)^{a-1}\end{align*} $$
$$ \begin{align*}\mathbb{P}( \mathbf{Geom}(\mu) = a ) = \frac{1}{\mu} \left( \frac{\mu-1}{\mu} \right)^{a-1}\end{align*} $$
for all
![]() $a \in \mathbb {N}+1$
. We use
$a \in \mathbb {N}+1$
. We use
![]() $\mathbf {Geom}(\mu )^n$
to denote a tuple of n independent, identically distributed (or iid for short) copies of
$\mathbf {Geom}(\mu )^n$
to denote a tuple of n independent, identically distributed (or iid for short) copies of
![]() $\mathbf {Geom}(\mu )$
, and use
$\mathbf {Geom}(\mu )$
, and use
![]() $\mathbf {X} \equiv \mathbf {Y}$
to denote the assertion that two random variables
$\mathbf {X} \equiv \mathbf {Y}$
to denote the assertion that two random variables
![]() $\mathbf {X},\mathbf {Y}$
have the same distribution. Thus, for instance,
$\mathbf {X},\mathbf {Y}$
have the same distribution. Thus, for instance,
whenever
![]() $\mathbf {a} \equiv \mathbf {Geom}(2)$
and
$\mathbf {a} \equiv \mathbf {Geom}(2)$
and
![]() $a \in \mathbb {N}+1$
, and more generally
$a \in \mathbb {N}+1$
, and more generally
whenever
![]() $\vec {\mathbf {a}} \equiv \mathbf {Geom}(2)^n$
and
$\vec {\mathbf {a}} \equiv \mathbf {Geom}(2)^n$
and
![]() $\vec a \in (\mathbb {N}+1)^n$
for some
$\vec a \in (\mathbb {N}+1)^n$
for some
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
In this paper, the only geometric random variables we will actually use are
![]() $\mathbf {Geom}(2)$
and
$\mathbf {Geom}(2)$
and
![]() $\mathbf {Geom}(4)$
.
$\mathbf {Geom}(4)$
.
We will then be guided by the following heuristic:
Heuristic 1.8 (Valuation heuristic)
If N is a ‘typical’ large odd natural number, and n is much smaller than
![]() $\log N$
, then the n-Syracuse valuation
$\log N$
, then the n-Syracuse valuation
![]() $\vec a^{(n)}(N)$
behaves like
$\vec a^{(n)}(N)$
behaves like
![]() $\mathbf {Geom}(2)^n$
.
$\mathbf {Geom}(2)^n$
.
We can make this heuristic precise as follows. Given two random variables
![]() $\mathbf {X},\mathbf {Y}$
taking values in the same discrete space R, we define the total variation
$\mathbf {X},\mathbf {Y}$
taking values in the same discrete space R, we define the total variation
![]() $d_{\operatorname {TV}}(\mathbf {X},\mathbf {Y})$
between the two variables to be the total variation of the difference in the probability measures; thus
$d_{\operatorname {TV}}(\mathbf {X},\mathbf {Y})$
between the two variables to be the total variation of the difference in the probability measures; thus
Note that
For any finite non-empty set R, let
![]() $\mathbf {Unif}(R)$
denote a uniformly distributed random variable on R. Then we have the following result, proven in Section 4:
$\mathbf {Unif}(R)$
denote a uniformly distributed random variable on R. Then we have the following result, proven in Section 4:
Proposition 1.9 (Distribution of n-Syracuse valuation)
Let
![]() $n \in \mathbb {N}$
, and let
$n \in \mathbb {N}$
, and let
![]() $\mathbf {N}$
be a random variable taking values in
$\mathbf {N}$
be a random variable taking values in
![]() $2\mathbb {N}+1$
. Suppose there exist an absolute constant
$2\mathbb {N}+1$
. Suppose there exist an absolute constant
![]() $c_0> 0$
and some natural number
$c_0> 0$
and some natural number
![]() $n' \geq (2+c_0) n$
such that
$n' \geq (2+c_0) n$
such that
![]() $\mathbf {N} \bmod 2^{n'}$
is approximately uniformly distributed in the odd residue classes
$\mathbf {N} \bmod 2^{n'}$
is approximately uniformly distributed in the odd residue classes
![]() $(2\mathbb {Z}+1)/2^{n'}\mathbb {Z}$
of
$(2\mathbb {Z}+1)/2^{n'}\mathbb {Z}$
of
![]() $\mathbb {Z}/2^\ell \mathbb {Z}$
, in the sense that
$\mathbb {Z}/2^\ell \mathbb {Z}$
, in the sense that
Then
for some absolute constant
![]() $c_1>0$
(depending on
$c_1>0$
(depending on
![]() $c_0$
). The implied constants in the asymptotic notation are also permitted to depend on
$c_0$
). The implied constants in the asymptotic notation are also permitted to depend on
![]() $c_0$
.
$c_0$
.
Informally, this proposition asserts that Heuristic 1.8 is justified whenever N is expected to be uniformly distributed modulo
![]() $2^{n'}$
for some
$2^{n'}$
for some
![]() $n'$
slightly larger than
$n'$
slightly larger than
![]() $2n$
. The hypothesis in equation (1.11) is somewhat stronger than what is actually needed for the conclusion in equation (1.12) to hold, but this formulation of the implication will suffice for our applications. We will apply this proposition in Section 5, not to the original logarithmic distribution
$2n$
. The hypothesis in equation (1.11) is somewhat stronger than what is actually needed for the conclusion in equation (1.12) to hold, but this formulation of the implication will suffice for our applications. We will apply this proposition in Section 5, not to the original logarithmic distribution
![]() $\mathbf {Log}(2\mathbb {N}+1 \cap [1,x])$
(which has too heavy a tail near
$\mathbf {Log}(2\mathbb {N}+1 \cap [1,x])$
(which has too heavy a tail near
![]() $1$
for the hypothesis in equation (1.11) to apply), but to the variant
$1$
for the hypothesis in equation (1.11) to apply), but to the variant
![]() $\mathbf {Log}( 2\mathbb {N}+1 \cap [y,y^\alpha ])$
for some large y and some
$\mathbf {Log}( 2\mathbb {N}+1 \cap [y,y^\alpha ])$
for some large y and some
![]() $\alpha>1$
close to
$\alpha>1$
close to
![]() $1$
.
$1$
.
Remark 1.10. Another standard way in the literature to justify Heuristic 1.8 is to consider the Syracuse dynamics on the
![]() $2$
-adic integers
$2$
-adic integers
![]() $\mathbb {Z}_2 := \varprojlim _m \mathbb {Z}/2^m\mathbb {Z}$
, or more precisely on the odd
$\mathbb {Z}_2 := \varprojlim _m \mathbb {Z}/2^m\mathbb {Z}$
, or more precisely on the odd
![]() $2$
-adics
$2$
-adics
![]() $2\mathbb {Z}_2+1$
. As the
$2\mathbb {Z}_2+1$
. As the
![]() $2$
-valuation
$2$
-valuation
![]() $\nu _2$
remains well defined on (almost all of)
$\nu _2$
remains well defined on (almost all of)
![]() $\mathbb {Z}_2$
, one can extend the Syracuse map
$\mathbb {Z}_2$
, one can extend the Syracuse map
![]() ${\operatorname {Syr}}$
to a map on
${\operatorname {Syr}}$
to a map on
![]() $2\mathbb {Z}_2+1$
. As is well known (see, e.g., [Reference Lagarias14]), the Haar probability measure on
$2\mathbb {Z}_2+1$
. As is well known (see, e.g., [Reference Lagarias14]), the Haar probability measure on
![]() $2\mathbb {Z}_2+1$
is preserved by this map, and if
$2\mathbb {Z}_2+1$
is preserved by this map, and if
![]() $\mathbf {Haar}(2\mathbb {Z}_2+1)$
is a random element of
$\mathbf {Haar}(2\mathbb {Z}_2+1)$
is a random element of
![]() $2\mathbb {Z}_2+1$
drawn using this measure, then it is not difficult (basically using the
$2\mathbb {Z}_2+1$
drawn using this measure, then it is not difficult (basically using the
![]() $2$
-adic analogue of Lemma 2.1 below) to show that the random variables
$2$
-adic analogue of Lemma 2.1 below) to show that the random variables
![]() $\nu _2( 3{\operatorname {Syr}}^{j}(\mathbf {Haar}(2\mathbb {Z}_2+1)) + 1)$
for
$\nu _2( 3{\operatorname {Syr}}^{j}(\mathbf {Haar}(2\mathbb {Z}_2+1)) + 1)$
for
![]() $j \in \mathbb {N}$
are iid copies of
$j \in \mathbb {N}$
are iid copies of
![]() $\mathbf {Geom}(2)$
. However, we will not use this
$\mathbf {Geom}(2)$
. However, we will not use this
![]() $2$
-adic formalism in this paper.
$2$
-adic formalism in this paper.
In practice, the offset
![]() $F_n(\vec a)$
is fairly small (in an Archimedean sense) when n is not too large; indeed, from equation (1.5), we have
$F_n(\vec a)$
is fairly small (in an Archimedean sense) when n is not too large; indeed, from equation (1.5), we have
for any
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $\vec a \in (\mathbb {N}+1)^n$
. For large N, we then conclude from equation (1.7) that we have the heuristic approximation
$\vec a \in (\mathbb {N}+1)^n$
. For large N, we then conclude from equation (1.7) that we have the heuristic approximation
and hence by Heuristic 1.8, we expect
![]() ${\operatorname {Syr}}^n(N)$
to behave statistically like
${\operatorname {Syr}}^n(N)$
to behave statistically like
if n is much smaller than
![]() $\log N$
. One can view the sequence
$\log N$
. One can view the sequence
![]() $n \mapsto n \log 3 - |\mathbf {Geom}(2)^n| \log 2$
as a simple random walk on
$n \mapsto n \log 3 - |\mathbf {Geom}(2)^n| \log 2$
as a simple random walk on
![]() $\mathbb {R}$
with negative drift
$\mathbb {R}$
with negative drift
![]() $\log 3 - 2 \log 2 = \log \frac {3}{4}$
. From the law of large numbers, we expect to have
$\log 3 - 2 \log 2 = \log \frac {3}{4}$
. From the law of large numbers, we expect to have
most of the time; thus we are led to the heuristic prediction
for typical N; indeed, from the central limit theorem or the Chernoff bound, we in fact expect the refinement
for ‘typical’ N. In particular, we expect the Syracuse orbit
![]() $N, {\operatorname {Syr}}(N), {\operatorname {Syr}}^2(N), \dots $
to decay geometrically in time for typical N, which underlies the usual heuristic argument supporting the truth of Conjecture 1.1; see [Reference Lagarias and Weiss16], [Reference Kontorovich and Lagarias10] for further discussion. We remark that the multiplicative inaccuracy of
$N, {\operatorname {Syr}}(N), {\operatorname {Syr}}^2(N), \dots $
to decay geometrically in time for typical N, which underlies the usual heuristic argument supporting the truth of Conjecture 1.1; see [Reference Lagarias and Weiss16], [Reference Kontorovich and Lagarias10] for further discussion. We remark that the multiplicative inaccuracy of
![]() $\exp ( O(n^{1/2}) )$
in equation (1.17) is the main reason why we work with logarithmic density instead of natural density in this paper (see also [Reference Kontorovich and Miller11], [Reference Lagarias and Soundararajan15] for a closely related ‘Benford’s law’ phenomenon).
$\exp ( O(n^{1/2}) )$
in equation (1.17) is the main reason why we work with logarithmic density instead of natural density in this paper (see also [Reference Kontorovich and Miller11], [Reference Lagarias and Soundararajan15] for a closely related ‘Benford’s law’ phenomenon).
1.3 Reduction to a stabilisation property for first passage locations
Roughly speaking, Proposition 1.9 lets one obtain good control on the Syracuse iterates
![]() ${\operatorname {Syr}}^n(N)$
for almost all N and for times n up to
${\operatorname {Syr}}^n(N)$
for almost all N and for times n up to
![]() $c \log N$
for a small absolute constant c. This already can be used in conjunction with a rigorous version of equation (1.16) or (1.17) to recover the previously mentioned result
$c \log N$
for a small absolute constant c. This already can be used in conjunction with a rigorous version of equation (1.16) or (1.17) to recover the previously mentioned result
![]() ${\operatorname {Syr}}_{\min }(N) \leq N^{1-c}$
for almost all N and some absolute constant
${\operatorname {Syr}}_{\min }(N) \leq N^{1-c}$
for almost all N and some absolute constant
![]() $c>0$
; see Section 5 for details. In the language of evolutionary partial differential equations, these types of results can be viewed as analogous to ‘almost sure’ local wellposedness results, in which one has good short-time control on the evolution for almost all choices of initial condition N.
$c>0$
; see Section 5 for details. In the language of evolutionary partial differential equations, these types of results can be viewed as analogous to ‘almost sure’ local wellposedness results, in which one has good short-time control on the evolution for almost all choices of initial condition N.
In this analogy, Theorem 1.6 then corresponds to an ‘almost sure’ almost global wellposedness result, where one needs to control the solution for times so large that the evolution gets arbitrary close to the bounded state
![]() $N=O(1)$
. To bootstrap from almost sure local wellposedness to almost sure almost global wellposedness, we were inspired by the work of Bourgain [Reference Bourgain4], who demonstrated an almost sure global wellposedness result for a certain nonlinear Schrödinger equation by combining local wellposedness theory with a construction of an invariant probability measure for the dynamics. Roughly speaking, the point was that the invariance of the measure would almost surely keep the solution in a ‘bounded’ region of the state space for arbitrarily long times, allowing one to iterate the local wellposedness theory indefinitely.
$N=O(1)$
. To bootstrap from almost sure local wellposedness to almost sure almost global wellposedness, we were inspired by the work of Bourgain [Reference Bourgain4], who demonstrated an almost sure global wellposedness result for a certain nonlinear Schrödinger equation by combining local wellposedness theory with a construction of an invariant probability measure for the dynamics. Roughly speaking, the point was that the invariance of the measure would almost surely keep the solution in a ‘bounded’ region of the state space for arbitrarily long times, allowing one to iterate the local wellposedness theory indefinitely.
In our context, we do not expect to have any useful invariant probability measures for the dynamics due to the geometric decay in equation (1.16) (and indeed Conjecture 1.5 would imply that the only invariant probability measure is the Dirac measure on
![]() $\{1\}$
). Instead, we can construct a family of probability measures
$\{1\}$
). Instead, we can construct a family of probability measures
![]() $\nu _x$
that are approximately transported to each other by certain iterations of the Syracuse map (by a variable amount of time). More precisely, given a threshold
$\nu _x$
that are approximately transported to each other by certain iterations of the Syracuse map (by a variable amount of time). More precisely, given a threshold
![]() $x \geq 1$
and an odd natural number
$x \geq 1$
and an odd natural number
![]() $N \in 2\mathbb {N}+1$
, define the first passage time
$N \in 2\mathbb {N}+1$
, define the first passage time
with the convention that
![]() $T_x(N) := +\infty $
if
$T_x(N) := +\infty $
if
![]() ${\operatorname {Syr}}^n(N)> x$
for all n. (Of course, if Conjecture 1.5 were true, this latter possibility could not occur, but we will not be assuming this conjecture in our arguments.) We then define the first passage location
${\operatorname {Syr}}^n(N)> x$
for all n. (Of course, if Conjecture 1.5 were true, this latter possibility could not occur, but we will not be assuming this conjecture in our arguments.) We then define the first passage location
with the (somewhat arbitrary and artificial) convention that
![]() ${\operatorname {Syr}}^\infty (N) := 1$
; thus
${\operatorname {Syr}}^\infty (N) := 1$
; thus
![]() ${\operatorname {Pass}}_x(N)$
is the first location of the Syracuse orbit
${\operatorname {Pass}}_x(N)$
is the first location of the Syracuse orbit
![]() ${\operatorname {Syr}}^{\mathbb {N}}(N)$
that falls inside
${\operatorname {Syr}}^{\mathbb {N}}(N)$
that falls inside
![]() $[1,x]$
, or
$[1,x]$
, or
![]() $1$
if no such location exists; if we ignore the latter possibility, then
$1$
if no such location exists; if we ignore the latter possibility, then
![]() ${\operatorname {Pass}}_x$
can be viewed as a further acceleration of the Collatz and Syracuse maps. We will also need a constant
${\operatorname {Pass}}_x$
can be viewed as a further acceleration of the Collatz and Syracuse maps. We will also need a constant
![]() $\alpha> 1$
sufficiently close to one. The precise choice of this parameter is not critical, but for sake of concreteness we will set
$\alpha> 1$
sufficiently close to one. The precise choice of this parameter is not critical, but for sake of concreteness we will set
The key proposition is then
Proposition 1.11 (Stabilisation of first passage)
For any y with
![]() $2\mathbb {N}+1 \cap [y,y^\alpha ]$
is non-empty (and in particular, for any sufficiently large y), let
$2\mathbb {N}+1 \cap [y,y^\alpha ]$
is non-empty (and in particular, for any sufficiently large y), let
![]() $\mathbf {N}_y$
be a random variable with distribution
$\mathbf {N}_y$
be a random variable with distribution
![]() $\mathbf {N}_y \equiv \mathbf {Log}( 2\mathbb {N}+1 \cap [y,y^\alpha ] )$
. Then for sufficiently large x, we have the estimates
$\mathbf {N}_y \equiv \mathbf {Log}( 2\mathbb {N}+1 \cap [y,y^\alpha ] )$
. Then for sufficiently large x, we have the estimates
for
![]() $y = x^\alpha , x^{\alpha ^2}$
, and also
$y = x^\alpha , x^{\alpha ^2}$
, and also
for some absolute constant
![]() $c>0$
. (The implied constants here are also absolute.)
$c>0$
. (The implied constants here are also absolute.)
Informally, this theorem asserts that the Syracuse orbits of
![]() $ \mathbf {N}_{x^\alpha } $
and
$ \mathbf {N}_{x^\alpha } $
and
![]() $ \mathbf {N}_{x^{\alpha ^2}}$
are almost indistinguishable from each other once they pass x, as long as one synchronises the orbits so that they simultaneously pass x for the first time. In Section 3, we shall see how Theorem 1.6 (and hence Theorem 1.3) follows from Proposition 1.11; basically the point is that equations (1.19) and (1.20) imply that the first passage map
$ \mathbf {N}_{x^{\alpha ^2}}$
are almost indistinguishable from each other once they pass x, as long as one synchronises the orbits so that they simultaneously pass x for the first time. In Section 3, we shall see how Theorem 1.6 (and hence Theorem 1.3) follows from Proposition 1.11; basically the point is that equations (1.19) and (1.20) imply that the first passage map
![]() ${\operatorname {Pass}}_x$
approximately maps the distribution
${\operatorname {Pass}}_x$
approximately maps the distribution
![]() $\nu _{x^\alpha }$
of
$\nu _{x^\alpha }$
of
![]() ${\operatorname {Pass}}_{x^{\alpha }}( \mathbf {N}_{x^{\alpha ^2}} )$
to the distribution
${\operatorname {Pass}}_{x^{\alpha }}( \mathbf {N}_{x^{\alpha ^2}} )$
to the distribution
![]() $\nu _x$
of
$\nu _x$
of
![]() ${\operatorname {Pass}}_{x}( \mathbf {N}_{x^{\alpha }} )$
, and one can then iterate this to map almost all of the probabilistic mass of
${\operatorname {Pass}}_{x}( \mathbf {N}_{x^{\alpha }} )$
, and one can then iterate this to map almost all of the probabilistic mass of
![]() $\mathbf {N}_y$
for large y to be arbitrarily close to the bounded state
$\mathbf {N}_y$
for large y to be arbitrarily close to the bounded state
![]() $N=O(1)$
. The implication is very general and does not use any particular properties of the Syracuse map beyond equations (1.19) and (1.20).
$N=O(1)$
. The implication is very general and does not use any particular properties of the Syracuse map beyond equations (1.19) and (1.20).
The estimate in equation (1.19) is easy to establish; it is equation (1.20) that is the most important and difficult conclusion of Proposition 1.11. We remark that the bound of
![]() $O(\log ^{-c} x)$
in equation (1.20) is stronger than is needed for this argument; any bound of the form
$O(\log ^{-c} x)$
in equation (1.20) is stronger than is needed for this argument; any bound of the form
![]() $O((\log \log x)^{-1-c})$
would have sufficed. Conversely, it may be possible to improve the bound in equation (1.20) further, perhaps all the way to
$O((\log \log x)^{-1-c})$
would have sufficed. Conversely, it may be possible to improve the bound in equation (1.20) further, perhaps all the way to
![]() $x^{-c}$
.
$x^{-c}$
.
1.4 Fine-scale mixing of Syracuse random variables
It remains to establish Proposition 1.11. Since the constant
![]() $\alpha $
in equation (1.18) is close to
$\alpha $
in equation (1.18) is close to
![]() $1$
, this proposition falls under the regime of a (refined) ‘local wellposedness’ result, since from the heuristic in equation (1.16) (or equation (1.17)), we expect the first passage time
$1$
, this proposition falls under the regime of a (refined) ‘local wellposedness’ result, since from the heuristic in equation (1.16) (or equation (1.17)), we expect the first passage time
![]() $T_x(\mathbf {N}_y)$
to be comparable to a small multiple of
$T_x(\mathbf {N}_y)$
to be comparable to a small multiple of
![]() $\log \mathbf {N}_y$
. Inspecting the iteration formula in equation (1.7), the behaviour of the n-Syracuse valuation
$\log \mathbf {N}_y$
. Inspecting the iteration formula in equation (1.7), the behaviour of the n-Syracuse valuation
![]() $\vec a^{(n)}(\mathbf {N}_y)$
for such times n is then well understood thanks to Proposition 1.9; the main remaining difficulty is to understand the behaviour of the n-Syracuse offset map
$\vec a^{(n)}(\mathbf {N}_y)$
for such times n is then well understood thanks to Proposition 1.9; the main remaining difficulty is to understand the behaviour of the n-Syracuse offset map
![]() $F_n\colon (\mathbb {N}+1)^n \to \mathbb {Z}[\frac {1}{2}]$
, and more specifically to analyse the distribution of the random variable
$F_n\colon (\mathbb {N}+1)^n \to \mathbb {Z}[\frac {1}{2}]$
, and more specifically to analyse the distribution of the random variable
![]() $F_n(\mathbf {Geom}(2)^n) \bmod 3^k$
for various
$F_n(\mathbf {Geom}(2)^n) \bmod 3^k$
for various
![]() $n,k$
, where by abuse of notation we use
$n,k$
, where by abuse of notation we use
![]() $x \mapsto x \bmod 3^k$
to denote the unique ring homomorphism from
$x \mapsto x \bmod 3^k$
to denote the unique ring homomorphism from
![]() $\mathbb {Z}[\frac {1}{2}]$
to
$\mathbb {Z}[\frac {1}{2}]$
to
![]() $\mathbb {Z}/3^k \mathbb {Z}$
(which in particular maps
$\mathbb {Z}/3^k \mathbb {Z}$
(which in particular maps
![]() $\frac {1}{2}$
to the inverse
$\frac {1}{2}$
to the inverse
![]() $\frac {3^k+1}{2} \bmod 3^k$
of
$\frac {3^k+1}{2} \bmod 3^k$
of
![]() $2 \bmod 3^k$
). Indeed, from equation (1.7), one has
$2 \bmod 3^k$
). Indeed, from equation (1.7), one has
whenever
![]() $0 \leq k \leq n$
and
$0 \leq k \leq n$
and
![]() $N \in 2\mathbb {N}+1$
. Thus, if
$N \in 2\mathbb {N}+1$
. Thus, if
![]() $n, \mathbf {N}, n', c_0$
obey the hypotheses of Proposition 1.9, one has
$n, \mathbf {N}, n', c_0$
obey the hypotheses of Proposition 1.9, one has
for all
![]() $0 \leq k \leq n$
. If we now define the Syracuse random variables
$0 \leq k \leq n$
. If we now define the Syracuse random variables
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
for
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
for
![]() $n \in \mathbb {N}$
to be random variables on the cyclic group
$n \in \mathbb {N}$
to be random variables on the cyclic group
![]() $\mathbb {Z}/3^n\mathbb {Z}$
with the distribution
$\mathbb {Z}/3^n\mathbb {Z}$
with the distribution
then from equation (1.5), we see that
whenever
![]() $k \leq n$
, and thus
$k \leq n$
, and thus
We thus see that the
![]() $3$
-adic distribution of the Syracuse orbit
$3$
-adic distribution of the Syracuse orbit
![]() ${\operatorname {Syr}}^{\mathbb {N}}(\mathbf {N})$
is controlled (initially, at least) by the random variables
${\operatorname {Syr}}^{\mathbb {N}}(\mathbf {N})$
is controlled (initially, at least) by the random variables
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
. The distribution of these random variables can be computed explicitly for any given n via the following recursive formula:
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
. The distribution of these random variables can be computed explicitly for any given n via the following recursive formula:
Lemma 1.12 (Recursive formula for Syracuse random variables)
For any
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $x \in \mathbb {Z}/3^{n+1}\mathbb {Z}$
, one has
$x \in \mathbb {Z}/3^{n+1}\mathbb {Z}$
, one has
 $$ \begin{align*}\mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^{n+1}\mathbb{Z}) = x ) = \frac{\sum_{1 \leq a \leq 2 \times 3^n: 2^a x = 1 \bmod 3} 2^{-a} \mathbb{P}\left( \mathbf{Syrac}(\mathbb{Z}/3^{n}\mathbb{Z})= \frac{2^a x-1}{3} \right)}{1 - 2^{-2 \times 3^n}},\end{align*} $$
$$ \begin{align*}\mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^{n+1}\mathbb{Z}) = x ) = \frac{\sum_{1 \leq a \leq 2 \times 3^n: 2^a x = 1 \bmod 3} 2^{-a} \mathbb{P}\left( \mathbf{Syrac}(\mathbb{Z}/3^{n}\mathbb{Z})= \frac{2^a x-1}{3} \right)}{1 - 2^{-2 \times 3^n}},\end{align*} $$
where
![]() $\frac {2^a x-1}{3}$
is viewed as an element of
$\frac {2^a x-1}{3}$
is viewed as an element of
![]() $\mathbb {Z}/3^n\mathbb {Z}$
.
$\mathbb {Z}/3^n\mathbb {Z}$
.
Proof. Let
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_{n+1}) \equiv \mathbf {Geom}(2)^{n+1}$
be
$(\mathbf {a}_1,\dots ,\mathbf {a}_{n+1}) \equiv \mathbf {Geom}(2)^{n+1}$
be
![]() $n+1$
iid copies of
$n+1$
iid copies of
![]() $\mathbf {Geom}(2)$
. From equation (1.5) (after relabeling the variables
$\mathbf {Geom}(2)$
. From equation (1.5) (after relabeling the variables
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_{n+1})$
in reverse order
$(\mathbf {a}_1,\dots ,\mathbf {a}_{n+1})$
in reverse order
![]() $(\mathbf {a}_{n+1},\dots ,\mathbf {a}_1)$
) we have
$(\mathbf {a}_{n+1},\dots ,\mathbf {a}_1)$
) we have
and thus we have
where
![]() $3\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
is viewed as an element of
$3\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
is viewed as an element of
![]() $\mathbb {Z}/3^{n+1}\mathbb {Z}$
, and the random variables
$\mathbb {Z}/3^{n+1}\mathbb {Z}$
, and the random variables
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z}), \mathbf {Geom}(2)$
on the right-hand side are understood to be independent. We therefore have
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z}), \mathbf {Geom}(2)$
on the right-hand side are understood to be independent. We therefore have
 $$ \begin{align*} \mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^{n+1}\mathbb{Z}) = x ) &= \sum_{a \in \mathbb{N}+1} 2^{-a} \mathbb{P}\left( \frac{3\mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z})+1}{2^a} = x \right) \\ &= \sum_{a \in \mathbb{N}+1: 2^a x = 1 \bmod 3} 2^{-a} \mathbb{P}\left( \mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z}) = \frac{2^a x-1}{3} \right). \end{align*} $$
$$ \begin{align*} \mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^{n+1}\mathbb{Z}) = x ) &= \sum_{a \in \mathbb{N}+1} 2^{-a} \mathbb{P}\left( \frac{3\mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z})+1}{2^a} = x \right) \\ &= \sum_{a \in \mathbb{N}+1: 2^a x = 1 \bmod 3} 2^{-a} \mathbb{P}\left( \mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z}) = \frac{2^a x-1}{3} \right). \end{align*} $$
By Euler’s theorem, the quantity
![]() $\frac {2^a x-1}{3} \in \mathbb {Z}/3^n \mathbb {Z}$
is periodic in a with period
$\frac {2^a x-1}{3} \in \mathbb {Z}/3^n \mathbb {Z}$
is periodic in a with period
![]() $2 \times 3^n$
. Splitting a into residue classes modulo
$2 \times 3^n$
. Splitting a into residue classes modulo
![]() $2 \times 3^n$
and using the geometric series formula, we obtain the claim.
$2 \times 3^n$
and using the geometric series formula, we obtain the claim.
Thus, for instance, we trivially have
![]() $\mathbf {Syrac}(\mathbb {Z}/3^0\mathbb {Z})$
takes the value
$\mathbf {Syrac}(\mathbb {Z}/3^0\mathbb {Z})$
takes the value
![]() $0 \bmod 1$
with probability
$0 \bmod 1$
with probability
![]() $1$
; then by the above lemma,
$1$
; then by the above lemma,
![]() $\mathbf {Syrac}(\mathbb {Z}/3\mathbb {Z})$
takes the values
$\mathbf {Syrac}(\mathbb {Z}/3\mathbb {Z})$
takes the values
![]() $0,1,2 \bmod 3$
with probabilities
$0,1,2 \bmod 3$
with probabilities
![]() $0, 1/3, 2/3$
respectively; another application of the above lemma then reveals that
$0, 1/3, 2/3$
respectively; another application of the above lemma then reveals that
![]() $\mathbf {Syrac}(\mathbb {Z}/3^2\mathbb {Z})$
takes the values
$\mathbf {Syrac}(\mathbb {Z}/3^2\mathbb {Z})$
takes the values
![]() $0,1,\dots ,8 \bmod 9$
with probabilities
$0,1,\dots ,8 \bmod 9$
with probabilities
respectively; and so forth. More generally, one can numerically compute the distribution of
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
exactly for small values of n, although the time and space required to do so increases exponentially with n.
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
exactly for small values of n, although the time and space required to do so increases exponentially with n.
Remark 1.13. One could view the Syracuse random variables
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
as projections
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
as projections
of a single random variable
![]() $\mathbf {Syrac}(\mathbb {Z}_3)$
taking values in the
$\mathbf {Syrac}(\mathbb {Z}_3)$
taking values in the
![]() $3$
-adics
$3$
-adics
![]() $\mathbb {Z}_3 := \varprojlim _n \mathbb {Z}/3^n\mathbb {Z}$
(equipped with the usual metric
$\mathbb {Z}_3 := \varprojlim _n \mathbb {Z}/3^n\mathbb {Z}$
(equipped with the usual metric
![]() $d(x,y) := 3^{-\nu _3(x-y)}$
), which can for instance be defined as
$d(x,y) := 3^{-\nu _3(x-y)}$
), which can for instance be defined as
 $$ \begin{align*} \mathbf{Syrac}(\mathbb{Z}_3) &\equiv \sum_{j=0}^\infty 3^j 2^{-\mathbf{a}_{[1,j+1]}}\\ &= 2^{-\mathbf{a}_1} + 3^1 2^{-\mathbf{a}_{[1,2]}} + 3^2 2^{-\mathbf{a}_{[1,3]}} + \dots \end{align*} $$
$$ \begin{align*} \mathbf{Syrac}(\mathbb{Z}_3) &\equiv \sum_{j=0}^\infty 3^j 2^{-\mathbf{a}_{[1,j+1]}}\\ &= 2^{-\mathbf{a}_1} + 3^1 2^{-\mathbf{a}_{[1,2]}} + 3^2 2^{-\mathbf{a}_{[1,3]}} + \dots \end{align*} $$
where
![]() $\mathbf {a}_1,\mathbf {a}_2,\dots $
are iid copies of
$\mathbf {a}_1,\mathbf {a}_2,\dots $
are iid copies of
![]() $\mathbf {Geom}(2)$
; note that this series converges in
$\mathbf {Geom}(2)$
; note that this series converges in
![]() $\mathbb {Z}_3$
, and the equivalence of distribution in equation (1.25) follows from equations (1.22) and (1.5) after reversingFootnote
4
the order of the tuple
$\mathbb {Z}_3$
, and the equivalence of distribution in equation (1.25) follows from equations (1.22) and (1.5) after reversingFootnote
4
the order of the tuple
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_n)$
(cf. (1.24)). One can view the distribution of
$(\mathbf {a}_1,\dots ,\mathbf {a}_n)$
(cf. (1.24)). One can view the distribution of
![]() $\mathbf {Syrac}(\mathbb {Z}_3)$
as the unique stationary measure for the discrete Markov processFootnote
5
on
$\mathbf {Syrac}(\mathbb {Z}_3)$
as the unique stationary measure for the discrete Markov processFootnote
5
on
![]() $\mathbb {Z}_3$
that maps each
$\mathbb {Z}_3$
that maps each
![]() $x \in \mathbb {Z}_3$
to
$x \in \mathbb {Z}_3$
to
![]() $\frac {3x+1}{2^{a}}$
for each
$\frac {3x+1}{2^{a}}$
for each
![]() $a \in \mathbb {N}+1$
with transition probability
$a \in \mathbb {N}+1$
with transition probability
![]() $2^{-a}$
(this fact is implicit in the proof of Lemma 1.12). However, we will not explicitly adopt the
$2^{-a}$
(this fact is implicit in the proof of Lemma 1.12). However, we will not explicitly adopt the
![]() $3$
-adic perspective in this paper, preferring to work instead with the finite projections
$3$
-adic perspective in this paper, preferring to work instead with the finite projections
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
of
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
of
![]() $\mathbf {Syrac}(\mathbb {Z}_3)$
.
$\mathbf {Syrac}(\mathbb {Z}_3)$
.
While the Syracuse random variables
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
fail to be uniformly distributed on
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
fail to be uniformly distributed on
![]() $\mathbb {Z}/3^n \mathbb {Z}$
, we can show that they do approach uniform distribution
$\mathbb {Z}/3^n \mathbb {Z}$
, we can show that they do approach uniform distribution
![]() $n \to \infty $
at fine scales (as measured in a
$n \to \infty $
at fine scales (as measured in a
![]() $3$
-adic sense), and this turns out to be the key ingredient needed to establish Proposition 1.11. More precisely, we will show
$3$
-adic sense), and this turns out to be the key ingredient needed to establish Proposition 1.11. More precisely, we will show
Proposition 1.14 (Fine-scale mixing of n-Syracuse offsets)
For all
![]() $1 \leq m \leq n$
one has
$1 \leq m \leq n$
one has
for any fixed
![]() $A>0$
, where the oscillation
$A>0$
, where the oscillation
![]() ${\operatorname {Osc}}_{m,n}( c_Y )_{Y \in \mathbb {Z}/3^n\mathbb {Z}}$
of a tuple of real numbers
${\operatorname {Osc}}_{m,n}( c_Y )_{Y \in \mathbb {Z}/3^n\mathbb {Z}}$
of a tuple of real numbers
![]() $c_Y \in \mathbb {R}$
indexed by
$c_Y \in \mathbb {R}$
indexed by
![]() $\mathbb {Z}/3^n\mathbb {Z}$
at
$\mathbb {Z}/3^n\mathbb {Z}$
at
![]() $3$
-adic scale
$3$
-adic scale
![]() $3^{-m}$
is defined by
$3^{-m}$
is defined by
 $$ \begin{align} {\operatorname{Osc}}_{m,n}( c_Y )_{Y \in \mathbb{Z}/3^n\mathbb{Z}} := \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} \left| c_Y - 3^{m-n} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} c_{Y'} \right|. \end{align} $$
$$ \begin{align} {\operatorname{Osc}}_{m,n}( c_Y )_{Y \in \mathbb{Z}/3^n\mathbb{Z}} := \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} \left| c_Y - 3^{m-n} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} c_{Y'} \right|. \end{align} $$
Informally, the above proposition asserts that the Syracuse random variable
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
is approximately uniformly distributed in ‘fine-scale’ or ‘high-frequency’ cosets
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
is approximately uniformly distributed in ‘fine-scale’ or ‘high-frequency’ cosets
![]() $Y + 3^m\mathbb {Z}/3^n\mathbb {Z}$
, after conditioning to the event
$Y + 3^m\mathbb {Z}/3^n\mathbb {Z}$
, after conditioning to the event
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z}) = Y \bmod 3^m$
. Indeed, one could write the left-hand side of equation (1.26) if desired as
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z}) = Y \bmod 3^m$
. Indeed, one could write the left-hand side of equation (1.26) if desired as
where the random variables
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z}), \mathbf {Unif}( 3^m\mathbb {Z}/3^n\mathbb {Z})$
are understood to be independent. In Section 5, we show how Proposition 1.11 (and hence Theorem 1.3) follows from Proposition 1.14 and Proposition 1.9.
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z}), \mathbf {Unif}( 3^m\mathbb {Z}/3^n\mathbb {Z})$
are understood to be independent. In Section 5, we show how Proposition 1.11 (and hence Theorem 1.3) follows from Proposition 1.14 and Proposition 1.9.
Remark 1.15. One can heuristically justify this mixing property as follows. The geometric random variable
![]() $\mathbf {Geom}(2)$
can be computed to have a Shannon entropy of
$\mathbf {Geom}(2)$
can be computed to have a Shannon entropy of
![]() $\log 4$
; thus, by asymptotic equipartition, the random variable
$\log 4$
; thus, by asymptotic equipartition, the random variable
![]() $\mathbf {Geom}(2)^n$
is expected to behave like a uniform distribution on
$\mathbf {Geom}(2)^n$
is expected to behave like a uniform distribution on
![]() $4^{n+o(n)}$
separate tuples in
$4^{n+o(n)}$
separate tuples in
![]() $(\mathbb {N}+1)^n$
. On the other hand, the range
$(\mathbb {N}+1)^n$
. On the other hand, the range
![]() $\mathbb {Z}/3^n\mathbb {Z}$
of the map
$\mathbb {Z}/3^n\mathbb {Z}$
of the map
![]() $\vec a \mapsto F_n(\vec a) \bmod 3^n$
only has cardinality
$\vec a \mapsto F_n(\vec a) \bmod 3^n$
only has cardinality
![]() $3^n$
. While this map does have substantial irregularities at coarse
$3^n$
. While this map does have substantial irregularities at coarse
![]() $3$
-adic scales (for instance, it always avoids the multiples of
$3$
-adic scales (for instance, it always avoids the multiples of
![]() $3$
), it is not expected to exhibit any such irregularity at fine scales, and so if one models this map by a random map from
$3$
), it is not expected to exhibit any such irregularity at fine scales, and so if one models this map by a random map from
![]() $4^{n+oW(n)}$
elements to
$4^{n+oW(n)}$
elements to
![]() $\mathbb {Z}/3^n\mathbb {Z}$
, one is led to the estimate in equation (1.26) (in fact, this argument predicts a stronger bound of
$\mathbb {Z}/3^n\mathbb {Z}$
, one is led to the estimate in equation (1.26) (in fact, this argument predicts a stronger bound of
![]() $\exp ( - cm )$
for some
$\exp ( - cm )$
for some
![]() $c>0$
, which we do not attempt to establish here).
$c>0$
, which we do not attempt to establish here).
Remark 1.16. In order to upgrade logarithmic density to natural density in our results, it seems necessary to strengthen Proposition 1.14 by establishing a suitable fine-scale mixing property of the entire random affine map
![]() ${\operatorname {Aff}}_{\mathbf {Geom}(2)^n}$
, as opposed to just the offset
${\operatorname {Aff}}_{\mathbf {Geom}(2)^n}$
, as opposed to just the offset
![]() $F_n(\mathbf {Geom}(2)^n)$
. This looks plausibly attainable from the methods in this paper, but we do not pursue this question here.
$F_n(\mathbf {Geom}(2)^n)$
. This looks plausibly attainable from the methods in this paper, but we do not pursue this question here.
To prove Proposition 1.14, we use a partial convolution structure present in the n-Syracuse offset map, together with Plancherel’s theorem, to reduce matters to establishing a superpolynomial decay bound for the characteristic function (or Fourier coefficients) of a Syracuse random variable
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
. More precisely, in Section 6, we derive Proposition 1.14 from
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
. More precisely, in Section 6, we derive Proposition 1.14 from
Proposition 1.17 (Decay of characteristic function)
Let
![]() $n \geq 1$
, and let
$n \geq 1$
, and let
![]() $\xi \in \mathbb {Z}/3^n\mathbb {Z}$
be not divisible by
$\xi \in \mathbb {Z}/3^n\mathbb {Z}$
be not divisible by
![]() $3$
. Then
$3$
. Then
for any fixed
![]() $A>0$
.
$A>0$
.
A key point here is that the implied constant in equation (1.28) is uniform in the parameters
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $\xi \in \mathbb {Z}/3^n\mathbb {Z}$
(assuming of course that
$\xi \in \mathbb {Z}/3^n\mathbb {Z}$
(assuming of course that
![]() $\xi $
is not divisible by
$\xi $
is not divisible by
![]() $3$
), although as indicated, we permit this constant to depend on A.
$3$
), although as indicated, we permit this constant to depend on A.
Remark 1.18. In the converse direction, it is not difficult to use the triangle inequality to establish the inequality
whenever
![]() $\xi $
is not a multiple of
$\xi $
is not a multiple of
![]() $3$
(so in particular the function
$3$
(so in particular the function
![]() $x \mapsto e^{-2\pi i \xi x/3^n}$
has mean zero on cosets of
$x \mapsto e^{-2\pi i \xi x/3^n}$
has mean zero on cosets of
![]() $3^{n-1}\mathbb {Z}/3^n\mathbb {Z}$
). Thus Proposition 1.17 and Proposition 1.14 are in fact equivalent. One could also equivalently phrase Proposition 1.17 in terms of the decay properties of the characteristic function of
$3^{n-1}\mathbb {Z}/3^n\mathbb {Z}$
). Thus Proposition 1.17 and Proposition 1.14 are in fact equivalent. One could also equivalently phrase Proposition 1.17 in terms of the decay properties of the characteristic function of
![]() $\mathbf {Syrac}(\mathbb {Z}_3)$
(which would be defined on the Pontryagin dual
$\mathbf {Syrac}(\mathbb {Z}_3)$
(which would be defined on the Pontryagin dual
![]() $\hat {\mathbb {Z}}_3 = \mathbb {Q}_3/\mathbb {Z}_3$
of
$\hat {\mathbb {Z}}_3 = \mathbb {Q}_3/\mathbb {Z}_3$
of
![]() $\mathbb {Z}_3$
), but we will not do so here.
$\mathbb {Z}_3$
), but we will not do so here.
The remaining task is to establish Proposition 1.17. This turns out to be the most difficult step in the argument, and is carried out in Section 7. From equations (1.5) and (1.22) and reversing the order of the random variables
![]() $\mathbf {a}_1,\dots ,\mathbf {a}_n$
(cf. equation (1.24)), we can describe the distribution of the Syracuse random variable by the formula
$\mathbf {a}_1,\dots ,\mathbf {a}_n$
(cf. equation (1.24)), we can describe the distribution of the Syracuse random variable by the formula
with
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_n) \equiv \mathbf {Geom}(2)^n$
; this also follows from equation (1.25). If this random variable
$(\mathbf {a}_1,\dots ,\mathbf {a}_n) \equiv \mathbf {Geom}(2)^n$
; this also follows from equation (1.25). If this random variable
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
was the sum of independent random variables, then the characteristic function of
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
was the sum of independent random variables, then the characteristic function of
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
would factor as something like a Riesz product of cosines, and its estimation would be straightforward. Unfortunately, the expression in equation (1.29) does not obviously resolve into such a sum of independent random variables; however, by grouping adjacent terms
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
would factor as something like a Riesz product of cosines, and its estimation would be straightforward. Unfortunately, the expression in equation (1.29) does not obviously resolve into such a sum of independent random variables; however, by grouping adjacent terms
![]() $3^{2j-2} 2^{-\mathbf {a}_{[1,2j-1]}}, 3^{2j-1} 2^{-\mathbf {a}_{[1,2j]}}$
in equation (1.29) into pairs, one can at least obtain a decomposition into the sum of independent expressions once one conditions on the sums
$3^{2j-2} 2^{-\mathbf {a}_{[1,2j-1]}}, 3^{2j-1} 2^{-\mathbf {a}_{[1,2j]}}$
in equation (1.29) into pairs, one can at least obtain a decomposition into the sum of independent expressions once one conditions on the sums
![]() $\mathbf {b}_j := \mathbf {a}_{2j-1}+\mathbf {a}_{2j}$
(which are iid copies of a Pascal distribution
$\mathbf {b}_j := \mathbf {a}_{2j-1}+\mathbf {a}_{2j}$
(which are iid copies of a Pascal distribution
![]() $\mathbf {Pascal}$
). This lets one express the characteristic functions as an average of products of cosines (times a phase), where the average is over trajectories of a certain random walk
$\mathbf {Pascal}$
). This lets one express the characteristic functions as an average of products of cosines (times a phase), where the average is over trajectories of a certain random walk
![]() $\mathbf {v}_1, \mathbf {v}_{[1,2]}, \mathbf {v}_{[1,3]},\dots $
in
$\mathbf {v}_1, \mathbf {v}_{[1,2]}, \mathbf {v}_{[1,3]},\dots $
in
![]() $\mathbb {Z}^2$
with increments in the first quadrant that we call a two-dimensional renewal process. If we color certain elements of
$\mathbb {Z}^2$
with increments in the first quadrant that we call a two-dimensional renewal process. If we color certain elements of
![]() $\mathbb {Z}^2$
‘white’ when the associated cosines are small, and ‘black’ otherwise, then the problem boils down to ensuring that this renewal process encounters a reasonably large number of white points (see Figure 3 in Section 7).
$\mathbb {Z}^2$
‘white’ when the associated cosines are small, and ‘black’ otherwise, then the problem boils down to ensuring that this renewal process encounters a reasonably large number of white points (see Figure 3 in Section 7).
From some elementary number theory, we will be able to describe the black regions of
![]() $\mathbb {Z}^2$
as a union of ‘triangles’
$\mathbb {Z}^2$
as a union of ‘triangles’
![]() $\Delta $
that are well separated from each other; again, see Figure 3. As a consequence, whenever the renewal process passes through a black triangle, it will very likely also pass through at least one white point after it exits the triangle. This argument is adequate so long as the triangles are not too large in size; however, for very large triangles, it does not produce a sufficient number of white points along the renewal process. However, it turns out that large triangles tend to be fairly well separated from each other (at least in the neighbourhood of even larger triangles), and this geometric observation allows one to close the argument.
$\Delta $
that are well separated from each other; again, see Figure 3. As a consequence, whenever the renewal process passes through a black triangle, it will very likely also pass through at least one white point after it exits the triangle. This argument is adequate so long as the triangles are not too large in size; however, for very large triangles, it does not produce a sufficient number of white points along the renewal process. However, it turns out that large triangles tend to be fairly well separated from each other (at least in the neighbourhood of even larger triangles), and this geometric observation allows one to close the argument.
As with Proposition 1.14, it is possible that the bound in Proposition 1.17 could be improved, perhaps to as far as
![]() $O(\exp (-cn))$
for some
$O(\exp (-cn))$
for some
![]() $c>0$
. However, we will not need or pursue such a bound here.
$c>0$
. However, we will not need or pursue such a bound here.
2 Notation and preliminaries
We use the asymptotic notation
![]() $X \ll Y$
,
$X \ll Y$
,
![]() $Y \gg X$
, or
$Y \gg X$
, or
![]() $X = O(Y)$
to denote the bound
$X = O(Y)$
to denote the bound
![]() $|X| \leq CY$
for an absolute constant C. We also write
$|X| \leq CY$
for an absolute constant C. We also write
![]() $X \asymp Y$
for
$X \asymp Y$
for
![]() $X \ll Y \ll X$
. We also use
$X \ll Y \ll X$
. We also use
![]() $c>0$
to denote various small constants that are allowed to vary from line to line or even within the same line. If we need the implied constants to depend on other parameters, we will indicate this by subscripts unless explicitly stated otherwise; thus, for instance,
$c>0$
to denote various small constants that are allowed to vary from line to line or even within the same line. If we need the implied constants to depend on other parameters, we will indicate this by subscripts unless explicitly stated otherwise; thus, for instance,
![]() $X \ll _A Y$
denotes the estimate
$X \ll _A Y$
denotes the estimate
![]() $|X| \leq C_A Y$
for some
$|X| \leq C_A Y$
for some
![]() $C_A$
depending on A.
$C_A$
depending on A.
If E is a set, we use
![]() $1_E$
to denote its indicator; thus
$1_E$
to denote its indicator; thus
![]() $1_E(n)$
equals
$1_E(n)$
equals
![]() $1$
when
$1$
when
![]() $n \in E$
and
$n \in E$
and
![]() $0$
otherwise. Similarly, if S is a statement, we define the indicator
$0$
otherwise. Similarly, if S is a statement, we define the indicator
![]() $1_S$
to equal
$1_S$
to equal
![]() $1$
when S is true and
$1$
when S is true and
![]() $0$
otherwise; thus, for instance,
$0$
otherwise; thus, for instance,
![]() $1_E(n) = 1_{n \in E}$
. If
$1_E(n) = 1_{n \in E}$
. If
![]() $E,F$
are two events, we use
$E,F$
are two events, we use
![]() $E \wedge F$
to denote their conjunction (the event that both
$E \wedge F$
to denote their conjunction (the event that both
![]() $E,F$
hold) and
$E,F$
hold) and
![]() $\overline {E}$
to denote the complement of E (the event that E does not hold).
$\overline {E}$
to denote the complement of E (the event that E does not hold).
The following alternate description of the n-Syracuse valuation
![]() $\vec a^{(n)}(N)$
(variants of which have frequently occurred in the literature on the Collatz conjecture; see, e.g., [Reference Sinai19]) will be useful.
$\vec a^{(n)}(N)$
(variants of which have frequently occurred in the literature on the Collatz conjecture; see, e.g., [Reference Sinai19]) will be useful.
Lemma 2.1 (Description of n-Syracuse valuation)
Let
![]() $N \in 2\mathbb {N}+1$
and
$N \in 2\mathbb {N}+1$
and
![]() $n \in \mathbb {N}$
. Then
$n \in \mathbb {N}$
. Then
![]() $\vec a^{(n)}(N)$
is the unique tuple
$\vec a^{(n)}(N)$
is the unique tuple
![]() $\vec a$
in
$\vec a$
in
![]() $(\mathbb {N}+1)^n$
for which
$(\mathbb {N}+1)^n$
for which
![]() ${\operatorname {Aff}}_{\vec a}(N) \in 2\mathbb {N}+1$
.
${\operatorname {Aff}}_{\vec a}(N) \in 2\mathbb {N}+1$
.
Proof. It is clear from equation (1.7) that
![]() ${\operatorname {Aff}}_{\vec a^{(n)}(N)} \in 2\mathbb {N}+1$
. It remains to prove uniqueness. The claim is easy for
${\operatorname {Aff}}_{\vec a^{(n)}(N)} \in 2\mathbb {N}+1$
. It remains to prove uniqueness. The claim is easy for
![]() $n=0$
, so suppose inductively that
$n=0$
, so suppose inductively that
![]() $n \geq 1$
and that uniqueness has already been established for
$n \geq 1$
and that uniqueness has already been established for
![]() $n-1$
. Suppose that we have found a tuple
$n-1$
. Suppose that we have found a tuple
![]() $\vec a \in (\mathbb {N}+1)^n$
for which
$\vec a \in (\mathbb {N}+1)^n$
for which
![]() ${\operatorname {Aff}}_{\vec a}(N)$
is an odd integer. Then
${\operatorname {Aff}}_{\vec a}(N)$
is an odd integer. Then
and thus
This implies that
![]() $3{\operatorname {Aff}}_{a_1,\dots ,a_{n-1}}(N)$
is an odd natural number. But from equation (1.3),
$3{\operatorname {Aff}}_{a_1,\dots ,a_{n-1}}(N)$
is an odd natural number. But from equation (1.3),
![]() ${\operatorname {Aff}}_{a_1,\dots ,a_{n-1}}(N)$
also lies in
${\operatorname {Aff}}_{a_1,\dots ,a_{n-1}}(N)$
also lies in
![]() $\mathbb {Z}[\frac {1}{2}]$
. The only way these claims can both be true is if
$\mathbb {Z}[\frac {1}{2}]$
. The only way these claims can both be true is if
![]() ${\operatorname {Aff}}_{a_1,\dots ,a_{n-1}}(N)$
is also an odd natural number, and then by induction
${\operatorname {Aff}}_{a_1,\dots ,a_{n-1}}(N)$
is also an odd natural number, and then by induction
![]() $(a_1,\dots ,a_{n-1}) = \vec a^{(n-1)}(N)$
, which by equation (1.7) implies that
$(a_1,\dots ,a_{n-1}) = \vec a^{(n-1)}(N)$
, which by equation (1.7) implies that
Inserting this into equation (2.1) and using the fact that
![]() ${\operatorname {Aff}}_{\vec a}(N)$
is odd, we obtain
${\operatorname {Aff}}_{\vec a}(N)$
is odd, we obtain
and hence by equation (1.8), we have
![]() $\vec a = \vec a^{(n)}$
as required.
$\vec a = \vec a^{(n)}$
as required.
We record the following concentration of measure bound of Chernoff type, which also bears some resemblance to a local limit theorem. We introduce the gaussian-type weights
for any
![]() $n \geq 0$
and
$n \geq 0$
and
![]() $x \in \mathbb {R}^d$
for some
$x \in \mathbb {R}^d$
for some
![]() $d \geq 1$
, where we adopt the convention that
$d \geq 1$
, where we adopt the convention that
![]() $\exp (-\infty )=0$
(so that
$\exp (-\infty )=0$
(so that
![]() $G_0(x) = \exp (-|x|)$
). Thus
$G_0(x) = \exp (-|x|)$
). Thus
![]() $G_n(x)$
is comparable to
$G_n(x)$
is comparable to
![]() $1$
for
$1$
for
![]() $x = O(n^{1/2})$
, decays in a gaussian fashion in the regime
$x = O(n^{1/2})$
, decays in a gaussian fashion in the regime
![]() $n^{1/2} \leq |x| \leq n$
and decays exponentially for
$n^{1/2} \leq |x| \leq n$
and decays exponentially for
![]() $|x| \geq n$
.
$|x| \geq n$
.
Lemma 2.2 (Chernoff type bound(
Let
![]() $d \in \mathbb {N}+1$
, and let
$d \in \mathbb {N}+1$
, and let
![]() $\mathbf {v}$
be a random variable taking values in
$\mathbf {v}$
be a random variable taking values in
![]() $\mathbb {Z}^d$
obeying the exponential tail condition
$\mathbb {Z}^d$
obeying the exponential tail condition
for all
![]() $\lambda \geq 0$
and some
$\lambda \geq 0$
and some
![]() $c_0>0$
. Assume the non-degeneracy condition that
$c_0>0$
. Assume the non-degeneracy condition that
![]() $\mathbf {v}$
is not almost surely concentrated on any coset of any proper subgroup of
$\mathbf {v}$
is not almost surely concentrated on any coset of any proper subgroup of
![]() $\mathbb {Z}^d$
. Let
$\mathbb {Z}^d$
. Let
![]() $\vec \mu := \mathbb {E} \mathbf {v} \in \mathbb {R}^d$
denote the mean of
$\vec \mu := \mathbb {E} \mathbf {v} \in \mathbb {R}^d$
denote the mean of
![]() $\mathbf {v}$
. In this lemma all implied constants, as well as the constant c, can depend on d,
$\mathbf {v}$
. In this lemma all implied constants, as well as the constant c, can depend on d,
![]() $c_0$
, and the distribution of
$c_0$
, and the distribution of
![]() $\mathbf {v}$
. Let
$\mathbf {v}$
. Let
![]() $n \in \mathbb {N}$
, and let
$n \in \mathbb {N}$
, and let
![]() $\mathbf {v}_1,\dots ,\mathbf {v}_n$
be n iid copies of
$\mathbf {v}_1,\dots ,\mathbf {v}_n$
be n iid copies of
![]() $\mathbf {v}$
. Following equation (1.6), we write
$\mathbf {v}$
. Following equation (1.6), we write
![]() $\mathbf {v}_{[1,n]} := \mathbf {v}_1 + \dots + \mathbf {v}_n$
.
$\mathbf {v}_{[1,n]} := \mathbf {v}_1 + \dots + \mathbf {v}_n$
.
-
(i) For any
 $\vec L \in \mathbb {Z}^d$
, one has
$\vec L \in \mathbb {Z}^d$
, one has  $$ \begin{align*}\mathbb{P}\left( \mathbf{v}_{[1,n]} = \vec L \right) \ll \frac{1}{(n+1)^{d/2}}G_n\left( c \left(\vec L - n \vec \mu\right) \right)\!.\end{align*} $$
$$ \begin{align*}\mathbb{P}\left( \mathbf{v}_{[1,n]} = \vec L \right) \ll \frac{1}{(n+1)^{d/2}}G_n\left( c \left(\vec L - n \vec \mu\right) \right)\!.\end{align*} $$
-
(ii) For any
 $\lambda \geq 0$
, one has
$\lambda \geq 0$
, one has  $$ \begin{align*}\mathbb{P}\left( |\mathbf{v}_{[1,n]}- n \vec \mu| \geq \lambda \right) \ll G_n( c \lambda ).\end{align*} $$
$$ \begin{align*}\mathbb{P}\left( |\mathbf{v}_{[1,n]}- n \vec \mu| \geq \lambda \right) \ll G_n( c \lambda ).\end{align*} $$
Thus, for instance for any
![]() $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
for every
![]() $L \in \mathbb {Z}$
, and
$L \in \mathbb {Z}$
, and
for any
![]() $\lambda \geq 0$
.
$\lambda \geq 0$
.
Proof. We use the Fourier-analytic (and complex-analytic) method. We may assume that n is positive since the claim is trivial for
![]() $n=0$
. We begin with (i). Let S denote the complex strip
$n=0$
. We begin with (i). Let S denote the complex strip
![]() $S := \{ z \in \mathbb {C}: |\mathrm {Re}(z)| < c_0 \}$
, then we can define the (complexified) moment generating function
$S := \{ z \in \mathbb {C}: |\mathrm {Re}(z)| < c_0 \}$
, then we can define the (complexified) moment generating function
![]() $M \colon S^d \to \mathbb {C}$
by the formula
$M \colon S^d \to \mathbb {C}$
by the formula
where
![]() $\cdot $
is the usual bilinear dot product. From equation (2.3) and Morera’s theorem, one verifies that this is a well-defined holomorphic function of d complex variables on
$\cdot $
is the usual bilinear dot product. From equation (2.3) and Morera’s theorem, one verifies that this is a well-defined holomorphic function of d complex variables on
![]() $S^d$
, which is periodic with respect to the lattice
$S^d$
, which is periodic with respect to the lattice
![]() $(2\pi i\mathbb {Z})^d$
. By Fourier inversion, we have
$(2\pi i\mathbb {Z})^d$
. By Fourier inversion, we have
By contour shifting, we then have
whenever
![]() $\vec \lambda = (\lambda _1,\dots ,\lambda _d) \in (-c_0,c_0)^d$
. By the triangle inequality, we thus have
$\vec \lambda = (\lambda _1,\dots ,\lambda _d) \in (-c_0,c_0)^d$
. By the triangle inequality, we thus have
From Taylor expansion and the non-degeneracy condition we have
 $$ \begin{align*}M(\vec z) = \exp\left( \vec z \cdot \vec \mu + \frac{1}{2} \Sigma(\vec z) + O(|\vec z|^3) \right)\end{align*} $$
$$ \begin{align*}M(\vec z) = \exp\left( \vec z \cdot \vec \mu + \frac{1}{2} \Sigma(\vec z) + O(|\vec z|^3) \right)\end{align*} $$
for all
![]() $\vec z \in S^d$
sufficiently close to
$\vec z \in S^d$
sufficiently close to
![]() $0$
, where
$0$
, where
![]() $\Sigma $
is a positive definite quadratic form (the covariance matrix of
$\Sigma $
is a positive definite quadratic form (the covariance matrix of
![]() $\mathbf {v}$
). From the non-degeneracy condition we also see that
$\mathbf {v}$
). From the non-degeneracy condition we also see that
![]() $|M(i\vec t)| < 1$
whenever
$|M(i\vec t)| < 1$
whenever
![]() $\vec t \in [-\pi ,\pi ]^d$
is not identically zero, hence by continuity
$\vec t \in [-\pi ,\pi ]^d$
is not identically zero, hence by continuity
![]() $|M(i\vec t + \vec \lambda )| \leq 1-c$
whenever
$|M(i\vec t + \vec \lambda )| \leq 1-c$
whenever
![]() $\vec t \in [-\pi ,\pi ]^d$
is bounded away from zero and
$\vec t \in [-\pi ,\pi ]^d$
is bounded away from zero and
![]() $\vec \lambda $
is sufficiently small. This implies the estimates
$\vec \lambda $
is sufficiently small. This implies the estimates
for all
![]() $\vec t \in [-\pi ,\pi ]^d$
and all sufficiently small
$\vec t \in [-\pi ,\pi ]^d$
and all sufficiently small
![]() $\vec \lambda \in \mathbb {R}^d$
. Thus we have
$\vec \lambda \in \mathbb {R}^d$
. Thus we have
 $$ \begin{align*} \mathbb{P}( \mathbf{v}_{[1,n]} = \vec L) &\ll \int_{[-\pi,\pi]^d} \exp\left( - \vec \lambda \cdot (\vec L-n\vec \mu) - c n|\vec t|^2 + O( n |\vec \lambda|^2 ) \right)\ d\vec t \\ &\ll n^{-1/2} \exp\left( - \vec \lambda \cdot (\vec L-n\vec \mu) + O( n |\vec \lambda|^2 ) \right). \end{align*} $$
$$ \begin{align*} \mathbb{P}( \mathbf{v}_{[1,n]} = \vec L) &\ll \int_{[-\pi,\pi]^d} \exp\left( - \vec \lambda \cdot (\vec L-n\vec \mu) - c n|\vec t|^2 + O( n |\vec \lambda|^2 ) \right)\ d\vec t \\ &\ll n^{-1/2} \exp\left( - \vec \lambda \cdot (\vec L-n\vec \mu) + O( n |\vec \lambda|^2 ) \right). \end{align*} $$
If
![]() $|\vec L-n\vec \mu | \leq n$
, we can set
$|\vec L-n\vec \mu | \leq n$
, we can set
![]() $\vec \lambda := c(\vec L-n\vec \mu ) / n$
for a sufficiently small c and obtain the claim; otherwise if
$\vec \lambda := c(\vec L-n\vec \mu ) / n$
for a sufficiently small c and obtain the claim; otherwise if
![]() $|\vec L-n\vec \mu |> n$
, we set
$|\vec L-n\vec \mu |> n$
, we set
![]() $\vec \lambda := c(\vec L-n\vec \mu )/|\vec L-n\vec \mu |$
for a sufficiently small c and again obtain the claim. This gives (i), and the claim (ii) then follows from summing in
$\vec \lambda := c(\vec L-n\vec \mu )/|\vec L-n\vec \mu |$
for a sufficiently small c and again obtain the claim. This gives (i), and the claim (ii) then follows from summing in
![]() $\vec L$
and applying the integral test.
$\vec L$
and applying the integral test.
Remark 2.3. Informally, the above lemma asserts that as a crude first approximation we have
and in particular
thus refining equation (1.15). The reader may wish to use this heuristic for subsequent arguments (for instance, in heuristically justifying equation (1.17)).
3 Reduction to stabilisation of first passage
In this section, we show how Theorem 1.6 follows from Proposition 1.11. In fact, we show that Proposition 1.11 implies a stronger claimFootnote 6 :
Theorem 3.1 (Alternate form of main theorem)
For
![]() $N_0 \geq 2$
and
$N_0 \geq 2$
and
![]() $x \geq 2$
, one has
$x \geq 2$
, one has
 $$ \begin{align*}\frac{1}{\log x} \sum_{N \in 2\mathbb{N}+1 \cap [1,x]: {\operatorname{Syr}}_{\min}(N)> N_0} \frac{1}{N} \ll \frac{1}{\log^c N_0}\end{align*} $$
$$ \begin{align*}\frac{1}{\log x} \sum_{N \in 2\mathbb{N}+1 \cap [1,x]: {\operatorname{Syr}}_{\min}(N)> N_0} \frac{1}{N} \ll \frac{1}{\log^c N_0}\end{align*} $$
or equivalently
 $$ \begin{align*}\mathbb{P}( {\operatorname{Syr}}_{\min}( \mathbf{Log}(2\mathbb{N}+1 \cap [1,x]) ) \leq N_0 ) \geq 1 - O\left( \frac{1}{\log^c N_0} \right)\!.\end{align*} $$
$$ \begin{align*}\mathbb{P}( {\operatorname{Syr}}_{\min}( \mathbf{Log}(2\mathbb{N}+1 \cap [1,x]) ) \leq N_0 ) \geq 1 - O\left( \frac{1}{\log^c N_0} \right)\!.\end{align*} $$
In particular, by equation (1.2), we have
 $$ \begin{align*}\mathbb{P}( {\operatorname{Col}}_{\min}( \mathbf{Log}(\mathbb{N}+1 \cap [1,x]) ) \leq N_0 ) \geq 1 - O\left( \frac{1}{\log^c N_0} \right)\end{align*} $$
$$ \begin{align*}\mathbb{P}( {\operatorname{Col}}_{\min}( \mathbf{Log}(\mathbb{N}+1 \cap [1,x]) ) \leq N_0 ) \geq 1 - O\left( \frac{1}{\log^c N_0} \right)\end{align*} $$
for all
![]() $x \geq 2$
.
$x \geq 2$
.
In other words, for
![]() $N_0 \geq 2$
, one has
$N_0 \geq 2$
, one has
![]() $\mathrm {Syr}_{\min }(N) \leq N_0$
for all N in a set of odd natural numbers of (lower) logarithmic density
$\mathrm {Syr}_{\min }(N) \leq N_0$
for all N in a set of odd natural numbers of (lower) logarithmic density
![]() $\frac {1}{2} - O( \log ^{-c} N_0)$
, and one also has
$\frac {1}{2} - O( \log ^{-c} N_0)$
, and one also has
![]() $\mathrm {Col}_{\min }(N) \leq N_0$
for all N in a set of positive natural numbers of (lower) logarithmic density
$\mathrm {Col}_{\min }(N) \leq N_0$
for all N in a set of positive natural numbers of (lower) logarithmic density
![]() $1 - O( \log ^{-c} N_0)$
.
$1 - O( \log ^{-c} N_0)$
.
Proof. We may assume that
![]() $N_0$
is larger than any given absolute constant, since the claim is trivial for bounded
$N_0$
is larger than any given absolute constant, since the claim is trivial for bounded
![]() $N_0$
. Let
$N_0$
. Let
![]() $E_{N_0} \subset 2\mathbb {N}+1$
denote the set
$E_{N_0} \subset 2\mathbb {N}+1$
denote the set
of starting positions N of Syracuse orbits that reach
![]() $N_0$
or below. Let
$N_0$
or below. Let
![]() $\alpha $
be defined by equation (1.18), let
$\alpha $
be defined by equation (1.18), let
![]() $x \geq 2$
, and let
$x \geq 2$
, and let
![]() $\mathbf {N}_y$
be the random variables from Proposition 1.11. Let
$\mathbf {N}_y$
be the random variables from Proposition 1.11. Let
![]() $B_x = B_{x,N_0}$
denote the event that
$B_x = B_{x,N_0}$
denote the event that
![]() $T_x(\mathbf {N}_{x^\alpha }) < +\infty $
and
$T_x(\mathbf {N}_{x^\alpha }) < +\infty $
and
![]() ${\operatorname {Pass}}_{x}(\mathbf {N}_{x^{\alpha }}) \in E_{N_0}$
. Informally, this is the event that the Syracuse orbit of
${\operatorname {Pass}}_{x}(\mathbf {N}_{x^{\alpha }}) \in E_{N_0}$
. Informally, this is the event that the Syracuse orbit of
![]() $\mathbf {N}_{x^\alpha }$
reaches x or below and then reaches
$\mathbf {N}_{x^\alpha }$
reaches x or below and then reaches
![]() $N_0$
or below. (For
$N_0$
or below. (For
![]() $x < N_0$
, the latter condition is automatic, while for
$x < N_0$
, the latter condition is automatic, while for
![]() $x \geq N_0$
, it is the former condition which is redundant.)
$x \geq N_0$
, it is the former condition which is redundant.)
Observe that if
![]() $T_x( \mathbf {N}_{x^{\alpha ^2}} ) < +\infty $
and
$T_x( \mathbf {N}_{x^{\alpha ^2}} ) < +\infty $
and
![]() ${\operatorname {Pass}}_x(\mathbf {N}_{x^{\alpha ^2}}) \in E_{N_0}$
, then
${\operatorname {Pass}}_x(\mathbf {N}_{x^{\alpha ^2}}) \in E_{N_0}$
, then
and
which implies that
In particular, the event
![]() $B_{x^\alpha }$
holds in this case. From this and equations (1.19), (1.20) and (1.10), we have
$B_{x^\alpha }$
holds in this case. From this and equations (1.19), (1.20) and (1.10), we have
 $$ \begin{align*} \mathbb{P}( B_{x^\alpha}) &\geq \mathbb{P}( {\operatorname{Pass}}_{x}(\mathbf{N}_{x^{\alpha^2}}) \in E_{N_0} \wedge T_{x}( \mathbf{N}_{x^{\alpha^2}} ) < +\infty ) \\ &\geq \mathbb{P}( {\operatorname{Pass}}_{x}(\mathbf{N}_{x^{\alpha^2}}) \in E_{N_0} ) - O( x^{-c} ) \\ &\geq \mathbb{P}( {\operatorname{Pass}}_{x}(\mathbf{N}_{x^{\alpha}}) \in E_{N_0} ) - O( \log^{-c} x ) \\ &\geq \mathbb{P}( B_x ) - O( \log^{-c} x ) \end{align*} $$
$$ \begin{align*} \mathbb{P}( B_{x^\alpha}) &\geq \mathbb{P}( {\operatorname{Pass}}_{x}(\mathbf{N}_{x^{\alpha^2}}) \in E_{N_0} \wedge T_{x}( \mathbf{N}_{x^{\alpha^2}} ) < +\infty ) \\ &\geq \mathbb{P}( {\operatorname{Pass}}_{x}(\mathbf{N}_{x^{\alpha^2}}) \in E_{N_0} ) - O( x^{-c} ) \\ &\geq \mathbb{P}( {\operatorname{Pass}}_{x}(\mathbf{N}_{x^{\alpha}}) \in E_{N_0} ) - O( \log^{-c} x ) \\ &\geq \mathbb{P}( B_x ) - O( \log^{-c} x ) \end{align*} $$
whenever x is larger than a suitable absolute constant (note that the
![]() $O(x^{-c})$
error can be absorbed into the
$O(x^{-c})$
error can be absorbed into the
![]() $O(\log ^{-c} x)$
term). In fact, the bound holds for all
$O(\log ^{-c} x)$
term). In fact, the bound holds for all
![]() $x \geq 2$
, since the estimate is trivial for bounded values of x.
$x \geq 2$
, since the estimate is trivial for bounded values of x.
Let
![]() $J = J(x,N_0)$
be the first natural number such that the quantity
$J = J(x,N_0)$
be the first natural number such that the quantity
![]() $y := x^{\alpha ^{-J}}$
is less than
$y := x^{\alpha ^{-J}}$
is less than
![]() $N_0^{1/\alpha }$
. Since
$N_0^{1/\alpha }$
. Since
![]() $N_0$
is assumed to be large, we then have (by replacing x with
$N_0$
is assumed to be large, we then have (by replacing x with
![]() $y^{\alpha ^{j-2}}$
in the preceding estimate) that
$y^{\alpha ^{j-2}}$
in the preceding estimate) that
for all
![]() $j=1,\dots ,J$
. The event
$j=1,\dots ,J$
. The event
![]() $B_{y^{\alpha ^{-1}}}$
occurs with probability
$B_{y^{\alpha ^{-1}}}$
occurs with probability
![]() $1 - O(y^{-c})$
, thanks to equation (1.19) and the fact that
$1 - O(y^{-c})$
, thanks to equation (1.19) and the fact that
![]() $\mathbf {N}_{y} \leq y^\alpha \leq N_0$
. Summing the telescoping series, we conclude that
$\mathbf {N}_{y} \leq y^\alpha \leq N_0$
. Summing the telescoping series, we conclude that
(note that the
![]() $O(y^{-c})$
error can be absorbed into the
$O(y^{-c})$
error can be absorbed into the
![]() $O( \log ^{-c} y )$
term). By construction,
$O( \log ^{-c} y )$
term). By construction,
![]() $y \geq N_0^{1/\alpha ^2}$
and
$y \geq N_0^{1/\alpha ^2}$
and
![]() $y^{\alpha ^J} = x$
, so
$y^{\alpha ^J} = x$
, so
If
![]() $B_{x^{1/\alpha }}$
holds, then
$B_{x^{1/\alpha }}$
holds, then
![]() ${\operatorname {Pass}}_{x^{1/\alpha }}( \mathbf {N}_x )$
lies in the Syracuse orbit
${\operatorname {Pass}}_{x^{1/\alpha }}( \mathbf {N}_x )$
lies in the Syracuse orbit
![]() ${\operatorname {Syr}}^{\mathbb {N}}(\mathbf {N}_x)$
, and thus
${\operatorname {Syr}}^{\mathbb {N}}(\mathbf {N}_x)$
, and thus
![]() ${\operatorname {Syr}}_{\min }(\mathbf {N}_x) \leq {\operatorname {Syr}}_{\min }({\operatorname {Pass}}_{x^{1/\alpha }}( \mathbf {N}_x )) \leq N_0$
. We conclude that for any
${\operatorname {Syr}}_{\min }(\mathbf {N}_x) \leq {\operatorname {Syr}}_{\min }({\operatorname {Pass}}_{x^{1/\alpha }}( \mathbf {N}_x )) \leq N_0$
. We conclude that for any
![]() $x \geq 2$
, one has
$x \geq 2$
, one has
By definition of
![]() $\mathbf {N}_x$
(and using the integral test to sum the harmonic series
$\mathbf {N}_x$
(and using the integral test to sum the harmonic series
![]() $\sum _{N \in 2\mathbb {N}+1 \cap [x,x^\alpha ]} \frac {1}{N}$
), we conclude that
$\sum _{N \in 2\mathbb {N}+1 \cap [x,x^\alpha ]} \frac {1}{N}$
), we conclude that
 $$ \begin{align} \sum_{N \in 2\mathbb{N}+1 \cap [x,x^\alpha]: {\operatorname{Syr}}_{\min}(N)> N_0} \frac{1}{N} \ll \frac{1}{\log^c N_0} \log x \end{align} $$
$$ \begin{align} \sum_{N \in 2\mathbb{N}+1 \cap [x,x^\alpha]: {\operatorname{Syr}}_{\min}(N)> N_0} \frac{1}{N} \ll \frac{1}{\log^c N_0} \log x \end{align} $$
for all
![]() $x \geq 2$
. Covering the interval
$x \geq 2$
. Covering the interval
![]() $2\mathbb {N}+1 \cap [1,x]$
by intervals of the form
$2\mathbb {N}+1 \cap [1,x]$
by intervals of the form
![]() $2\mathbb {N}+1 \cap [y,y^\alpha ]$
for various y, we obtain the claim.
$2\mathbb {N}+1 \cap [y,y^\alpha ]$
for various y, we obtain the claim.
Now let
![]() $f\colon 2\mathbb {N}+1 \to [0,+\infty )$
be such that
$f\colon 2\mathbb {N}+1 \to [0,+\infty )$
be such that
![]() $\lim _{N \to \infty } f(N) = +\infty $
. Set
$\lim _{N \to \infty } f(N) = +\infty $
. Set
![]() $\tilde f(x) := \inf _{N \in 2\mathbb {N}+1: N \geq x} f(N)$
, then
$\tilde f(x) := \inf _{N \in 2\mathbb {N}+1: N \geq x} f(N)$
, then
![]() $\tilde f(x) \to \infty $
as
$\tilde f(x) \to \infty $
as
![]() $x \to \infty $
. Applying Theorem 3.1 with
$x \to \infty $
. Applying Theorem 3.1 with
![]() $N_0 := \tilde f(x)$
, we conclude that
$N_0 := \tilde f(x)$
, we conclude that
 $$ \begin{align*}\sum_{N \in 2\mathbb{N}+1 \cap [1,x]: {\operatorname{Syr}}_{\min}(N)> f(N)} \frac{1}{N} \ll \frac{1}{\log^c \tilde f(x)} \log x\end{align*} $$
$$ \begin{align*}\sum_{N \in 2\mathbb{N}+1 \cap [1,x]: {\operatorname{Syr}}_{\min}(N)> f(N)} \frac{1}{N} \ll \frac{1}{\log^c \tilde f(x)} \log x\end{align*} $$
for all sufficiently large x. Since
![]() $\frac {1}{\log ^c\tilde f(x)}$
goes to zero as
$\frac {1}{\log ^c\tilde f(x)}$
goes to zero as
![]() $x \to \infty $
, we conclude from telescoping series that the set
$x \to \infty $
, we conclude from telescoping series that the set
![]() $\{ N \in 2\mathbb {N}+1: {\operatorname {Syr}}_{\min }(N)> f(N) \}$
has zero logarithmic density, and Theorem 1.6 follows.
$\{ N \in 2\mathbb {N}+1: {\operatorname {Syr}}_{\min }(N)> f(N) \}$
has zero logarithmic density, and Theorem 1.6 follows.
4
 $3$
-adic distribution of iterates
$3$
-adic distribution of iterates
In this section, we establish Proposition 1.9. Let
![]() $n, \mathbf {N}, c_0, n'$
be as in that proposition; in particular,
$n, \mathbf {N}, c_0, n'$
be as in that proposition; in particular,
![]() $n' \geq (2+c_0) n$
. In this section, we allow implied constants in the asymptotic notation, as well as the constants
$n' \geq (2+c_0) n$
. In this section, we allow implied constants in the asymptotic notation, as well as the constants
![]() $c>0$
, to depend on
$c>0$
, to depend on
![]() $c_0$
.
$c_0$
.
We first need a tail bound on the size of the n-Syracuse valuation
![]() $\vec a^{(n)}(\mathbf {N})$
:
$\vec a^{(n)}(\mathbf {N})$
:
Lemma 4.1 (Tail bound)
We have
Proof. Write
![]() $\vec a^{(n)}(\mathbf {N}) = (\mathbf {a}_1,\dots ,\mathbf {a}_n)$
, then we may split
$\vec a^{(n)}(\mathbf {N}) = (\mathbf {a}_1,\dots ,\mathbf {a}_n)$
, then we may split
 $$ \begin{align*}\mathbb{P}( |\vec a^{(n)}(\mathbf{N})| \geq n' ) = \sum_{k=0}^{n-1} \mathbb{P}( \mathbf{a}_{[1,k]} < n' \leq \mathbf{a}_{[1,k+1]} )\end{align*} $$
$$ \begin{align*}\mathbb{P}( |\vec a^{(n)}(\mathbf{N})| \geq n' ) = \sum_{k=0}^{n-1} \mathbb{P}( \mathbf{a}_{[1,k]} < n' \leq \mathbf{a}_{[1,k+1]} )\end{align*} $$
(using the summation convention in equation (1.6)), and so it suffices to show that
for each
![]() $0 \leq k \leq n-1$
.
$0 \leq k \leq n-1$
.
From Lemma 2.1 and equation (1.3), we see that
 $$ \begin{align*}3^{k+1} 2^{- \mathbf{a}_{[1,k+1]}} \mathbf{N} + \sum_{i=1}^{k+1} 3^{k+1-i} 2^{-\mathbf{a}_{[i,k+1]}}\end{align*} $$
$$ \begin{align*}3^{k+1} 2^{- \mathbf{a}_{[1,k+1]}} \mathbf{N} + \sum_{i=1}^{k+1} 3^{k+1-i} 2^{-\mathbf{a}_{[i,k+1]}}\end{align*} $$
is an odd integer, and thus
 $$ \begin{align*}3^{k+1} \mathbf{N} + \sum_{i=1}^{k+1} 3^{k+1-i} 2^{\mathbf{a}_{[1,i-1]}}\end{align*} $$
$$ \begin{align*}3^{k+1} \mathbf{N} + \sum_{i=1}^{k+1} 3^{k+1-i} 2^{\mathbf{a}_{[1,i-1]}}\end{align*} $$
is a multiple of
![]() $2^{\mathbf {a}_{[1,k+1]}}$
. In particular, when the event
$2^{\mathbf {a}_{[1,k+1]}}$
. In particular, when the event
![]() $\mathbf {a}_{[1,k]} < n' \leq \mathbf {a}_{[1,k+1]}$
holds, one has
$\mathbf {a}_{[1,k]} < n' \leq \mathbf {a}_{[1,k+1]}$
holds, one has
 $$ \begin{align*}3^{k+1} \mathbf{N} + \sum_{i=1}^{k+1} 3^{k+1-i} 2^{\mathbf{a}_{[1,i-1]}} = 0 \bmod 2^{n'}.\end{align*} $$
$$ \begin{align*}3^{k+1} \mathbf{N} + \sum_{i=1}^{k+1} 3^{k+1-i} 2^{\mathbf{a}_{[1,i-1]}} = 0 \bmod 2^{n'}.\end{align*} $$
Thus, if one conditions to the event
![]() $\mathbf {a}_j = a_j, j=1,\dots ,k$
for some positive integers
$\mathbf {a}_j = a_j, j=1,\dots ,k$
for some positive integers
![]() $a_1,\dots ,a_k$
, then
$a_1,\dots ,a_k$
, then
![]() $\mathbf {N}$
is constrained to a single residue class
$\mathbf {N}$
is constrained to a single residue class
![]() $b \bmod 2^{n'}$
depending on
$b \bmod 2^{n'}$
depending on
![]() $a_1,\dots ,a_k$
(because
$a_1,\dots ,a_k$
(because
![]() $3^{k+1}$
is invertible in the ring
$3^{k+1}$
is invertible in the ring
![]() $\mathbb {Z}/2^{n'}\mathbb {Z}$
). From equations (1.11) and (1.9), we have the quite crude estimate
$\mathbb {Z}/2^{n'}\mathbb {Z}$
). From equations (1.11) and (1.9), we have the quite crude estimate
and hence
 $$ \begin{align*}\mathbb{P}( \mathbf{a}_{[1,k]} \leq n' < \mathbf{a}_{[1,k+1]} ) \ll \sum_{a_1,\dots,a_k \in \mathbb{N}+1: a_{[1,k]} < n'} 2^{-n'}.\end{align*} $$
$$ \begin{align*}\mathbb{P}( \mathbf{a}_{[1,k]} \leq n' < \mathbf{a}_{[1,k+1]} ) \ll \sum_{a_1,\dots,a_k \in \mathbb{N}+1: a_{[1,k]} < n'} 2^{-n'}.\end{align*} $$
The tuples
![]() $(a_1,\dots ,a_k)$
in the above sum are in one-to-one correspondence with the k-element subsets
$(a_1,\dots ,a_k)$
in the above sum are in one-to-one correspondence with the k-element subsets
![]() $\{ a_1, a_{[1,2]},\dots ,a_{[1,k]}\}$
of
$\{ a_1, a_{[1,2]},\dots ,a_{[1,k]}\}$
of
![]() $\{1,\dots ,n'-1\}$
, and hence have cardinality
$\{1,\dots ,n'-1\}$
, and hence have cardinality
![]() $\binom {n'-1}{k}$
; thus
$\binom {n'-1}{k}$
; thus
 $$ \begin{align*}\mathbb{P}( \mathbf{a}_{[1,k]} < n' \leq \mathbf{a}_{[1,k+1]} ) \ll 2^{-n'} \binom{n'-1}{k}.\end{align*} $$
$$ \begin{align*}\mathbb{P}( \mathbf{a}_{[1,k]} < n' \leq \mathbf{a}_{[1,k+1]} ) \ll 2^{-n'} \binom{n'-1}{k}.\end{align*} $$
Since
![]() $k \leq n-1$
and
$k \leq n-1$
and
![]() $n' \geq (2+c_0) n$
, the right-hand side is
$n' \geq (2+c_0) n$
, the right-hand side is
![]() $O(2^{-cn})$
by Stirling’s formula (one can also use the Chernoff inequality for the sum of
$O(2^{-cn})$
by Stirling’s formula (one can also use the Chernoff inequality for the sum of
![]() $n'-1$
Bernoulli random variables
$n'-1$
Bernoulli random variables
![]() $\mathbf {Ber}(\frac {1}{2})$
, or Lemma 2.2). The claim follows.
$\mathbf {Ber}(\frac {1}{2})$
, or Lemma 2.2). The claim follows.
From Lemma 2.2, we also have
From equation (1.9) and the triangle inequality, we therefore have
 $$ \begin{align*}d_{\operatorname{TV}}(\vec a^{(n)}(\mathbf{N}), \mathbf{Geom}(2)^n) = \sum_{\vec a \in (\mathbb{N}+1)^n: |\vec a| < m} |\mathbb{P}(\vec a^{(n)}(\mathbf{N})=\vec a) - \mathbb{P}(\mathbf{Geom}(2)^n=\vec a)| + O( 2^{-cn} ).\end{align*} $$
$$ \begin{align*}d_{\operatorname{TV}}(\vec a^{(n)}(\mathbf{N}), \mathbf{Geom}(2)^n) = \sum_{\vec a \in (\mathbb{N}+1)^n: |\vec a| < m} |\mathbb{P}(\vec a^{(n)}(\mathbf{N})=\vec a) - \mathbb{P}(\mathbf{Geom}(2)^n=\vec a)| + O( 2^{-cn} ).\end{align*} $$
From Definition 1.7, we have
so it remains to show that
 $$ \begin{align} \sum_{\vec a \in (\mathbb{N}+1)^n: |\vec a| < m} |\mathbb{P}(\vec a^{(n)}(\mathbf{N})=\vec a) - 2^{-|\vec a|}| \ll 2^{-cn}. \end{align} $$
$$ \begin{align} \sum_{\vec a \in (\mathbb{N}+1)^n: |\vec a| < m} |\mathbb{P}(\vec a^{(n)}(\mathbf{N})=\vec a) - 2^{-|\vec a|}| \ll 2^{-cn}. \end{align} $$
By Lemma 2.1, the event
![]() $\vec a^{(n)}(\mathbf {N})=\vec a$
occurs precisely when
$\vec a^{(n)}(\mathbf {N})=\vec a$
occurs precisely when
![]() ${\operatorname {Aff}}_{\vec a}(\mathbf {N})$
is an odd integer, which by equation (1.3), we may write (for
${\operatorname {Aff}}_{\vec a}(\mathbf {N})$
is an odd integer, which by equation (1.3), we may write (for
![]() $\vec a = (a_1,\dots ,a_n)$
) as
$\vec a = (a_1,\dots ,a_n)$
) as
Equivalently one has
This constrains
![]() $\mathbf {N}$
to a single odd residue class modulo
$\mathbf {N}$
to a single odd residue class modulo
![]() $2^{|\vec a|+1}$
. For
$2^{|\vec a|+1}$
. For
![]() $|\vec a| < n'$
, the probability of falling in this class can be computed using equations (1.11) and (1.9) as
$|\vec a| < n'$
, the probability of falling in this class can be computed using equations (1.11) and (1.9) as
![]() $2^{-|\vec a|} + O( 2^{-n'} )$
. The left-hand side of equation (4.1) is then bounded by
$2^{-|\vec a|} + O( 2^{-n'} )$
. The left-hand side of equation (4.1) is then bounded by
 $$ \begin{align*}\ll 2^{-n'} \# \{ \vec a \in (\mathbb{N}+1)^n: |\vec a| < n' \} = 2^{-n'} \binom{n'-1}{n}.\end{align*} $$
$$ \begin{align*}\ll 2^{-n'} \# \{ \vec a \in (\mathbb{N}+1)^n: |\vec a| < n' \} = 2^{-n'} \binom{n'-1}{n}.\end{align*} $$
The claim now follows from Stirling’s formula (or Chernoff’s inequality), as in the proof of Lemma 4.1. This completes the proof of Proposition 1.9.
5 Reduction to fine-scale mixing of the n-Syracuse offset map
We are now ready to derive Proposition 1.11 (and thus Theorem 1.3) assuming Proposition 1.14. Let x be sufficiently large. We take y to be either
![]() $x^\alpha $
or
$x^\alpha $
or
![]() $x^{\alpha ^2}$
. From the heuristic in equation (1.16) (or equation (1.17)), we expect the first passage time
$x^{\alpha ^2}$
. From the heuristic in equation (1.16) (or equation (1.17)), we expect the first passage time
![]() ${\operatorname {Pass}}_x(\mathbf {N}_y)$
to be roughly
${\operatorname {Pass}}_x(\mathbf {N}_y)$
to be roughly
with high probability. Now introduce the quantities
 $$ \begin{align} n_0 := \left\lfloor \frac{\log x}{10 \log 2} \right\rfloor \end{align} $$
$$ \begin{align} n_0 := \left\lfloor \frac{\log x}{10 \log 2} \right\rfloor \end{align} $$
(so that
![]() $2^{n_0} \asymp x^{0.1}$
) and
$2^{n_0} \asymp x^{0.1}$
) and
 $$ \begin{align} m_0 := \left\lfloor \frac{\alpha-1}{100} \log x \right\rfloor \!. \end{align} $$
$$ \begin{align} m_0 := \left\lfloor \frac{\alpha-1}{100} \log x \right\rfloor \!. \end{align} $$
Since the random variable
![]() $\mathbf {N}_y$
takes values in
$\mathbf {N}_y$
takes values in
![]() $[y,y^\alpha ]$
, we see from equation (1.18) that we would expect the bounds
$[y,y^\alpha ]$
, we see from equation (1.18) that we would expect the bounds
to hold with high probability. We will use these parameters
![]() $m_0, n_0$
to help control the distribution of
$m_0, n_0$
to help control the distribution of
![]() $T_x(\mathbf {N}_y)$
and
$T_x(\mathbf {N}_y)$
and
![]() ${\operatorname {Pass}}_x(\mathbf {N}_y)$
in order to prove equations (1.19) and (1.20).
${\operatorname {Pass}}_x(\mathbf {N}_y)$
in order to prove equations (1.19) and (1.20).
We begin with the proof of equation (1.19). Let
![]() $n_0$
be defined by equation (5.1). Since
$n_0$
be defined by equation (5.1). Since
![]() $\mathbf {N}_y \equiv \mathbf {Log}(2\mathbb {N}+1 \cap [y,y^\alpha ])$
, a routine application of the integral test reveals that
$\mathbf {N}_y \equiv \mathbf {Log}(2\mathbb {N}+1 \cap [y,y^\alpha ])$
, a routine application of the integral test reveals that
(with plenty of room to spare), hence by Proposition 1.9
In particular, by equation (1.10) and Lemma 2.2, we have
(recall we allow c to vary even within the same line). On the other hand, from equations (1.7) and (1.5), we have
and hence if
![]() $|\vec a^{(n_0)}(\mathbf {N}_y)|> 1.9 n$
, then
$|\vec a^{(n_0)}(\mathbf {N}_y)|> 1.9 n$
, then
From equations (5.1) and (1.18) and a brief calculation, the right-hand side is
![]() $O(x^{0.99})$
(say). In particular, for x large enough, we have
$O(x^{0.99})$
(say). In particular, for x large enough, we have
and hence
![]() $T_x(\mathbf {N}_y) \leq n_0 < +\infty $
whenever
$T_x(\mathbf {N}_y) \leq n_0 < +\infty $
whenever
![]() $|\vec a^{(n_0)}(\mathbf {N}_y)|> 1.9 n_0$
(cf., the upper bound in equation (5.3)). The claim in equation (1.19) now follows from equation (5.5).
$|\vec a^{(n_0)}(\mathbf {N}_y)|> 1.9 n_0$
(cf., the upper bound in equation (5.3)). The claim in equation (1.19) now follows from equation (5.5).
Remark 5.1. This argument already establishes that
![]() ${\operatorname {Syr}}_{\min }(N) \leq N^\theta $
for almost all N for any
${\operatorname {Syr}}_{\min }(N) \leq N^\theta $
for almost all N for any
![]() $\theta> 1/\alpha $
; by optimising the numerical exponents in this argument one can eventually recover the results of Korec [Reference Korec9] mentioned in the introduction. It also shows that most odd numbers do not lie in a periodic Syracuse orbit, or more precisely that
$\theta> 1/\alpha $
; by optimising the numerical exponents in this argument one can eventually recover the results of Korec [Reference Korec9] mentioned in the introduction. It also shows that most odd numbers do not lie in a periodic Syracuse orbit, or more precisely that
Indeed, the above arguments show that outside of an event of probability
![]() $x^{-c}$
, one has
$x^{-c}$
, one has
![]() ${\operatorname {Syr}}^{\mathbf {m}}(\mathbf {N}_y) \leq x$
for some
${\operatorname {Syr}}^{\mathbf {m}}(\mathbf {N}_y) \leq x$
for some
![]() $\mathbf {m} \leq n_0$
, which we can assume to be minimal amongst all such
$\mathbf {m} \leq n_0$
, which we can assume to be minimal amongst all such
![]() $\mathbf {m}$
. If
$\mathbf {m}$
. If
![]() ${\operatorname {Syr}}^n(\mathbf {N}_y) = \mathbf {N}_y$
for some n, we then have
${\operatorname {Syr}}^n(\mathbf {N}_y) = \mathbf {N}_y$
for some n, we then have
for
![]() $\mathbf {M} := {\operatorname {Syr}}^{\mathbf {m}}(\mathbf {N}_y) \in [1,x]$
that generates a periodic Syracuse orbit with period
$\mathbf {M} := {\operatorname {Syr}}^{\mathbf {m}}(\mathbf {N}_y) \in [1,x]$
that generates a periodic Syracuse orbit with period
![]() $n(\mathbf {M})$
. (This period
$n(\mathbf {M})$
. (This period
![]() $n(\mathbf {M})$
could be extremely large, and the periodic orbit could attain values much larger than x or y, but we will not need any upper bounds on the period in our arguments, other than that it is finite.) The number of possible pairs
$n(\mathbf {M})$
could be extremely large, and the periodic orbit could attain values much larger than x or y, but we will not need any upper bounds on the period in our arguments, other than that it is finite.) The number of possible pairs
![]() $(\mathbf {M},\mathbf {m})$
obtained in this fashion is
$(\mathbf {M},\mathbf {m})$
obtained in this fashion is
![]() $O(xn_0)$
. By equation (5.6), the pair
$O(xn_0)$
. By equation (5.6), the pair
![]() $(\mathbf {M},\mathbf {m})$
uniquely determines
$(\mathbf {M},\mathbf {m})$
uniquely determines
![]() $\mathbf {N}_y$
. Thus, outside of the aforementioned event, a periodic orbit is only possible for at most
$\mathbf {N}_y$
. Thus, outside of the aforementioned event, a periodic orbit is only possible for at most
![]() $O(xn_0)$
possible values of
$O(xn_0)$
possible values of
![]() $\mathbf {N}_y$
; as this is much smaller than y, we thus see that a periodic orbit is only attained with probability
$\mathbf {N}_y$
; as this is much smaller than y, we thus see that a periodic orbit is only attained with probability
![]() $O(x^{-c})$
, giving the claim. It is then a routine matter to then deduce that almost all positive integers do not lie in a periodic Collatz orbit; we leave the details to the interested reader.
$O(x^{-c})$
, giving the claim. It is then a routine matter to then deduce that almost all positive integers do not lie in a periodic Collatz orbit; we leave the details to the interested reader.
Now we establish equation (1.20). By equation (1.10), it suffices to show that for
![]() $E \subset 2\mathbb {N}+1 \cap [1,x]$
, that
$E \subset 2\mathbb {N}+1 \cap [1,x]$
, that
for some quantity Q that can depend on
![]() $x,\alpha ,E$
but is independent of whether y is equal to
$x,\alpha ,E$
but is independent of whether y is equal to
![]() $x^\alpha $
or
$x^\alpha $
or
![]() $x^{\alpha ^2}$
(note that this bound automatically forces
$x^{\alpha ^2}$
(note that this bound automatically forces
![]() $Q = O(1)$
when x is large, so the first error term
$Q = O(1)$
when x is large, so the first error term
![]() $O(\log ^{-c} x) Q$
on the right-hand side may be absorbed into the second term
$O(\log ^{-c} x) Q$
on the right-hand side may be absorbed into the second term
![]() $O(\log ^{-c} x)$
). The strategy is to manipulate the left-hand side of equation (5.7) into an expression that involves the Syracuse random variables
$O(\log ^{-c} x)$
). The strategy is to manipulate the left-hand side of equation (5.7) into an expression that involves the Syracuse random variables
![]() $\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
for various n (in a range
$\mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
for various n (in a range
![]() $I_y$
depending on y) plus a small error, and then appeal to Proposition 1.14 to remove the dependence on n and hence on y in the main term. The main difficulty is that the first passage location
$I_y$
depending on y) plus a small error, and then appeal to Proposition 1.14 to remove the dependence on n and hence on y in the main term. The main difficulty is that the first passage location
![]() ${\operatorname {Pass}}_x(\mathbf {N}_y)$
involves a first passage time
${\operatorname {Pass}}_x(\mathbf {N}_y)$
involves a first passage time
![]() $n = T_x(\mathbf {N}_y)$
whose value is not known in advance; but by stepping back in time by a fixed number of steps
$n = T_x(\mathbf {N}_y)$
whose value is not known in advance; but by stepping back in time by a fixed number of steps
![]() $m_0$
, we will be able to express the left-hand side of equation (5.7) (up to negligible errors) without having to explicitly refer to the first passage time.
$m_0$
, we will be able to express the left-hand side of equation (5.7) (up to negligible errors) without having to explicitly refer to the first passage time.
The first step is to establish the following approximate formula for the left-hand side of equation (5.7).
Proposition 5.2 (Approximate formula)
Let
![]() $E \subset 2\mathbb {N}+1 \cap [1,x]$
and
$E \subset 2\mathbb {N}+1 \cap [1,x]$
and
![]() $y = x^\alpha , x^{\alpha ^2}$
. Then we have
$y = x^\alpha , x^{\alpha ^2}$
. Then we have
 $$ \begin{align} \mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = \sum_{n \in I_y} \sum_{\vec a \in {\mathcal A}^{(n-m_0)}} \sum_{M \in E'} \mathbb{P}( {\operatorname{Aff}}_{\vec a}(\mathbf{N}_y) = M ) + O( \log^{-c} x ) \end{align} $$
$$ \begin{align} \mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = \sum_{n \in I_y} \sum_{\vec a \in {\mathcal A}^{(n-m_0)}} \sum_{M \in E'} \mathbb{P}( {\operatorname{Aff}}_{\vec a}(\mathbf{N}_y) = M ) + O( \log^{-c} x ) \end{align} $$
where
![]() $I_y$
is the interval
$I_y$
is the interval
 $$ \begin{align} I_y := \left[\frac{\log( y / x )}{\log \frac{4}{3}} + \log^{0.8} x, \frac{\log( y^\alpha / x )}{\log \frac{4}{3}} - \log^{0.8} x\right]\! , \end{align} $$
$$ \begin{align} I_y := \left[\frac{\log( y / x )}{\log \frac{4}{3}} + \log^{0.8} x, \frac{\log( y^\alpha / x )}{\log \frac{4}{3}} - \log^{0.8} x\right]\! , \end{align} $$
![]() $E'$
is the set of odd natural numbers
$E'$
is the set of odd natural numbers
![]() $M \in 2\mathbb {N}+1$
such that
$M \in 2\mathbb {N}+1$
such that
![]() $T_x(M) = m_0$
and
$T_x(M) = m_0$
and
![]() ${\operatorname {Pass}}_x(M) \in E$
with
${\operatorname {Pass}}_x(M) \in E$
with
and for any natural number
![]() $n'$
,
$n'$
,
![]() ${\mathcal A}^{(n')} \subset (\mathbb {N}+1)^{n'}$
denotes the set of all tuples
${\mathcal A}^{(n')} \subset (\mathbb {N}+1)^{n'}$
denotes the set of all tuples
![]() $(a_1,\dots ,a_{n'}) \in (\mathbb {N}+1)^{n'}$
such that
$(a_1,\dots ,a_{n'}) \in (\mathbb {N}+1)^{n'}$
such that
for all
![]() $0 \leq n \leq n'$
.
$0 \leq n \leq n'$
.
A key point in the formula in equation (5.8) is that the right-hand side does not involve the passage time
![]() $T_x(\mathbf {N}_y)$
or the first passage location
$T_x(\mathbf {N}_y)$
or the first passage location
![]() ${\operatorname {Pass}}_x(\mathbf {N}_y)$
, and the dependence on whether y is equal to
${\operatorname {Pass}}_x(\mathbf {N}_y)$
, and the dependence on whether y is equal to
![]() $x^\alpha $
or
$x^\alpha $
or
![]() $x^{\alpha ^2}$
is confined to the range
$x^{\alpha ^2}$
is confined to the range
![]() $I_y$
of the summation variable n, as well as the input
$I_y$
of the summation variable n, as well as the input
![]() $\mathbf {N}_y$
of the affine map
$\mathbf {N}_y$
of the affine map
![]() ${\operatorname {Aff}}_{\vec a}$
. (In particular, note that the set
${\operatorname {Aff}}_{\vec a}$
. (In particular, note that the set
![]() $E'$
does not depend on y.) We also observe from equations (5.9), (5.1) and (5.2) that
$E'$
does not depend on y.) We also observe from equations (5.9), (5.1) and (5.2) that
![]() $I_y \subset [m_0,n_0]$
, which is consistent with the heuristic in equation (5.3).
$I_y \subset [m_0,n_0]$
, which is consistent with the heuristic in equation (5.3).
Proof. Fix E, and write
![]() $\vec a^{(n_0)}(\mathbf {N}_y) = (\mathbf {a}_1,\dots ,\mathbf {a}_{n_0})$
. From equations (5.4) and (1.10) and Lemma 2.2, we see that for every
$\vec a^{(n_0)}(\mathbf {N}_y) = (\mathbf {a}_1,\dots ,\mathbf {a}_{n_0})$
. From equations (5.4) and (1.10) and Lemma 2.2, we see that for every
![]() $0 \leq n \leq n_0$
, one has
$0 \leq n \leq n_0$
, one has
Hence, if
![]() ${\mathcal A}^{(n_0)}$
is the set defined in the proposition, we see from the union bound that
${\mathcal A}^{(n_0)}$
is the set defined in the proposition, we see from the union bound that
(say); this can be viewed as a rigorous analogue of the heuristic in equation (2.5). Hence
Suppose that
![]() $\vec a^{(n_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n_0)}$
. For any
$\vec a^{(n_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n_0)}$
. For any
![]() $0 \leq n \leq n_0$
, we have from equations (1.7) and (1.13) that
$0 \leq n \leq n_0$
, we have from equations (1.7) and (1.13) that
and hence by equations (5.11) and (5.1) and some calculation
In particular, from equation (5.11), one has
for all
![]() $0 \leq n \leq n_0$
, which can be viewed as a rigorous version of the heuristic in equation (1.17). With regards to Figure 1, equation (5.14) asserts that the Syracuse orbit stays close to the dashed line.
$0 \leq n \leq n_0$
, which can be viewed as a rigorous version of the heuristic in equation (1.17). With regards to Figure 1, equation (5.14) asserts that the Syracuse orbit stays close to the dashed line.

Figure 1 The Syracuse orbit
![]() $n \mapsto \mathrm {Syr}^n(\mathbf {N}_y)$
, where the vertical axis is drawn in shifted log-scale. The diagonal lines have slope
$n \mapsto \mathrm {Syr}^n(\mathbf {N}_y)$
, where the vertical axis is drawn in shifted log-scale. The diagonal lines have slope
![]() $-\log (4/3)$
. For times n up to
$-\log (4/3)$
. For times n up to
![]() $n_0$
, the orbit usually stays close to the dashed line and hence usually lies between the two dotted diagonal lines; in particular, the first passage time
$n_0$
, the orbit usually stays close to the dashed line and hence usually lies between the two dotted diagonal lines; in particular, the first passage time
![]() $T_x(\mathbf {N}_y)$
will usually lie in the interval
$T_x(\mathbf {N}_y)$
will usually lie in the interval
![]() $I_y$
. Outside of a rare exceptional event, for any given
$I_y$
. Outside of a rare exceptional event, for any given
![]() $n \in I_y$
,
$n \in I_y$
,
![]() ${\operatorname {Syr}}^{n-m}(\mathbf {N}_y)$
will lie in
${\operatorname {Syr}}^{n-m}(\mathbf {N}_y)$
will lie in
![]() $E'$
if and only if
$E'$
if and only if
![]() $n = T_x(\mathbf {N}_y)$
and
$n = T_x(\mathbf {N}_y)$
and
![]() ${\operatorname {Syr}}^n(\mathbf {N}_y)$
lies in E; equivalently, outside of a rare exceptional event,
${\operatorname {Syr}}^n(\mathbf {N}_y)$
lies in E; equivalently, outside of a rare exceptional event,
![]() ${\operatorname {Pass}}_x(\mathbf {N}_y)$
lies in E if and only if
${\operatorname {Pass}}_x(\mathbf {N}_y)$
lies in E if and only if
![]() ${\operatorname {Syr}}^{n-m}(\mathbf {N}_y)$
lies in
${\operatorname {Syr}}^{n-m}(\mathbf {N}_y)$
lies in
![]() $E'$
for precisely one
$E'$
for precisely one
![]() $n \in I_y$
.
$n \in I_y$
.
As
![]() $T_x(\mathbf {N}_y)$
is the first time n for which
$T_x(\mathbf {N}_y)$
is the first time n for which
![]() ${\operatorname {Syr}}^n(\mathbf {N}_y) \leq x$
, the estimate in equation (5.14) gives an approximation
${\operatorname {Syr}}^n(\mathbf {N}_y) \leq x$
, the estimate in equation (5.14) gives an approximation
 $$ \begin{align} T_x(\mathbf{N}_y) = \frac{\log( \mathbf{N}_y / x )}{\log \frac{4}{3}} + O( \log^{0.6} x); \end{align} $$
$$ \begin{align} T_x(\mathbf{N}_y) = \frac{\log( \mathbf{N}_y / x )}{\log \frac{4}{3}} + O( \log^{0.6} x); \end{align} $$
note from equations (5.1) and (1.18) and a brief calculation that the right-hand side automatically lies between
![]() $0$
and
$0$
and
![]() $n_0$
if x is large enough. In particular, if
$n_0$
if x is large enough. In particular, if
![]() $I_y$
is the interval in equation (5.9), then equation (5.14) will imply that
$I_y$
is the interval in equation (5.9), then equation (5.14) will imply that
![]() $T_x(\mathbf {N}_y) \in I_y$
whenever
$T_x(\mathbf {N}_y) \in I_y$
whenever
a straightforward calculation using the integral test (and equation (5.12)) then shows that
Again, see Figure 1. Note from equations (5.1) and (5.2) that
![]() $I_y \subset [m_0,n_0]$
; compare with equation (5.3).
$I_y \subset [m_0,n_0]$
; compare with equation (5.3).
Now suppose that n is an element of
![]() $I_y$
. In particular,
$I_y$
. In particular,
![]() $n \geq m_0$
. We observe the following implications:
$n \geq m_0$
. We observe the following implications:
-
• If
 $T_x(\mathbf {N}_y) = n$
, then certainly
$T_x(\mathbf {N}_y) = n$
, then certainly
 $T_x( {\operatorname {Syr}}^{n-m_0}(\mathbf {N}_y) ) = m_0$
.
$T_x( {\operatorname {Syr}}^{n-m_0}(\mathbf {N}_y) ) = m_0$
. -
• Conversely, if
 $T_x( {\operatorname {Syr}}^{n-m_0}(\mathbf {N}_y) ) = m_0$
and
$T_x( {\operatorname {Syr}}^{n-m_0}(\mathbf {N}_y) ) = m_0$
and
 $\vec a^{(n_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n_0)}$
, we have
$\vec a^{(n_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n_0)}$
, we have
 ${\operatorname {Syr}}^n(\mathbf {N}_y) \leq x < {\operatorname {Syr}}^{n-1}(\mathbf {N}_y)$
, which by equation (5.14) forces which by equations (5.15) and (5.2) implies that
${\operatorname {Syr}}^n(\mathbf {N}_y) \leq x < {\operatorname {Syr}}^{n-1}(\mathbf {N}_y)$
, which by equation (5.14) forces which by equations (5.15) and (5.2) implies that $$ \begin{align*}n = \frac{\log( \mathbf{N}_y / x )}{\log \frac{4}{3}} + O( \log^{0.6} x),\end{align*} $$
$$ \begin{align*}n = \frac{\log( \mathbf{N}_y / x )}{\log \frac{4}{3}} + O( \log^{0.6} x),\end{align*} $$
 $T_x(\mathbf {N}_y) \geq n - m_0$
, and hence
$T_x(\mathbf {N}_y) \geq n - m_0$
, and hence  $$ \begin{align*}T_x(\mathbf{N}_y) = n - m_0 + T_x({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)) = n.\end{align*} $$
$$ \begin{align*}T_x(\mathbf{N}_y) = n - m_0 + T_x({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)) = n.\end{align*} $$
We conclude that for any
![]() $n \in I_y$
, the event
$n \in I_y$
, the event
holds precisely when the event
does. From equation (5.16), we therefore have the estimate
 $$ \begin{align*}\mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = \sum_{n \in I_y} \mathbb{P}(B_{n,y}) + O( \log^{-c} x ). \end{align*} $$
$$ \begin{align*}\mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = \sum_{n \in I_y} \mathbb{P}(B_{n,y}) + O( \log^{-c} x ). \end{align*} $$
With
![]() $E'$
the set defined in the proposition, we observe the following implications:
$E'$
the set defined in the proposition, we observe the following implications:
-
• If
 $B_{n,y}$
occurs, then from equations (5.14) and (5.15), we have and hence
$B_{n,y}$
occurs, then from equations (5.14) and (5.15), we have and hence $$ \begin{align*}{\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) = \exp( O( \log^{0.6} x)) (3/4)^{T_x(\mathbf{N}_y)-m_0} \mathbf{N}_y = \exp( O( \log^{0.6} x)) (4/3)^{m_0} x\end{align*} $$
(5.17)
$$ \begin{align*}{\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) = \exp( O( \log^{0.6} x)) (3/4)^{T_x(\mathbf{N}_y)-m_0} \mathbf{N}_y = \exp( O( \log^{0.6} x)) (4/3)^{m_0} x\end{align*} $$
(5.17) $$ \begin{align} \left( {\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) \in E'\right) \wedge \left(\vec a^{(n_0)}(\mathbf{N}_y) \in {\mathcal A}^{(n_0)}\right). \end{align} $$
$$ \begin{align} \left( {\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) \in E'\right) \wedge \left(\vec a^{(n_0)}(\mathbf{N}_y) \in {\mathcal A}^{(n_0)}\right). \end{align} $$
-
• Conversely, if equation (5.17) holds, then from equation (5.14), we have
for all $$ \begin{align*}{\operatorname{Syr}}^{n'}(\mathbf{N}_y) = \exp(O(\log^{0.6} x)) (4/3)^{n-m_0-n'} {\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) \geq \exp(O(\log^{0.6} x)) {\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)\end{align*} $$
$$ \begin{align*}{\operatorname{Syr}}^{n'}(\mathbf{N}_y) = \exp(O(\log^{0.6} x)) (4/3)^{n-m_0-n'} {\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) \geq \exp(O(\log^{0.6} x)) {\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)\end{align*} $$
 $0 \leq n' \leq n-m_0$
, and hence by equation (5.10) for all
$0 \leq n' \leq n-m_0$
, and hence by equation (5.10) for all $$ \begin{align*}{\operatorname{Syr}}^{n'}(\mathbf{N}_y)> x\end{align*} $$
$$ \begin{align*}{\operatorname{Syr}}^{n'}(\mathbf{N}_y)> x\end{align*} $$
 $0 \leq n' \leq n-m_0$
. We conclude that thanks to the definition of
$0 \leq n' \leq n-m_0$
. We conclude that thanks to the definition of $$ \begin{align*}{\operatorname{Pass}}_x(\mathbf{N}_y) = n-m_0 + {\operatorname{Pass}}_x({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)) = n\end{align*} $$
$$ \begin{align*}{\operatorname{Pass}}_x(\mathbf{N}_y) = n-m_0 + {\operatorname{Pass}}_x({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)) = n\end{align*} $$
 $E'$
, and hence also In particular, the event
$E'$
, and hence also In particular, the event $$ \begin{align*}T_x(\mathbf{N}_y) = T_x({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)) \in E.\end{align*} $$
$$ \begin{align*}T_x(\mathbf{N}_y) = T_x({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y)) \in E.\end{align*} $$
 $B_{n,y}$
holds.
$B_{n,y}$
holds.
We conclude that we have the equality of events
for any
![]() $n \in I_y$
. Since the event
$n \in I_y$
. Since the event
![]() $\vec a^{(n_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n_0)}$
is contained in the event
$\vec a^{(n_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n_0)}$
is contained in the event
![]() $\vec a^{(n-m_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n-m_0)}$
, we conclude from equation (5.12) that
$\vec a^{(n-m_0)}(\mathbf {N}_y) \in {\mathcal A}^{(n-m_0)}$
, we conclude from equation (5.12) that
 $$ \begin{align*}\mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = \sum_{n \in I_y} \mathbb{P}\left( \left({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) \in E'\right) \wedge \left(\vec a^{(n-m_0)}(\mathbf{N}_y) \in {\mathcal A}^{(n-m_0)}\right) \right) + O( \log^{-c} x ).\end{align*} $$
$$ \begin{align*}\mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = \sum_{n \in I_y} \mathbb{P}\left( \left({\operatorname{Syr}}^{n-m_0}(\mathbf{N}_y) \in E'\right) \wedge \left(\vec a^{(n-m_0)}(\mathbf{N}_y) \in {\mathcal A}^{(n-m_0)}\right) \right) + O( \log^{-c} x ).\end{align*} $$
Suppose that
![]() $\vec a = (a_1,\dots ,a_{n-m})$
is a tuple in
$\vec a = (a_1,\dots ,a_{n-m})$
is a tuple in
![]() ${\mathcal A}^{(n-m)}$
, and
${\mathcal A}^{(n-m)}$
, and
![]() $M \in E'$
. From Lemma 2.1, we see that the event
$M \in E'$
. From Lemma 2.1, we see that the event
![]() $\left ({\operatorname {Syr}}^{n-m_0}(\mathbf {N}_y) = M\right ) \wedge \left (\vec a^{(n-m_0)}(\mathbf {N}_y) = \vec a\right )$
holds if and only if
$\left ({\operatorname {Syr}}^{n-m_0}(\mathbf {N}_y) = M\right ) \wedge \left (\vec a^{(n-m_0)}(\mathbf {N}_y) = \vec a\right )$
holds if and only if
![]() ${\operatorname {Aff}}_{\vec a}( \mathbf {N}_y) \in E'$
, and the claim in equation (5.8) follows.
${\operatorname {Aff}}_{\vec a}( \mathbf {N}_y) \in E'$
, and the claim in equation (5.8) follows.
Now we compute the right-hand side of equation (5.8). Let
![]() $n \in I_y$
,
$n \in I_y$
,
![]() $\vec a \in {\mathcal A}^{(n-m_0)}$
, and
$\vec a \in {\mathcal A}^{(n-m_0)}$
, and
![]() $M \in E'$
. Then by equation (1.3), the event
$M \in E'$
. Then by equation (1.3), the event
![]() ${\operatorname {Aff}}_{\vec a}(\mathbf {N}_y) = M$
is only non-empty when
${\operatorname {Aff}}_{\vec a}(\mathbf {N}_y) = M$
is only non-empty when
Conversely, if equation (5.18) holds, then
![]() ${\operatorname {Aff}}_{\vec a}(\mathbf {N}_y) = M$
holds precisely when
${\operatorname {Aff}}_{\vec a}(\mathbf {N}_y) = M$
holds precisely when
Note from equations (5.11) and (1.13) that the right-hand side of equation (5.19) is equal to
which by equations (5.10) and (5.1) simplifies to
Since
![]() $n \in I_y$
, we conclude from equation (5.9) that the right-hand side of equation (5.19) lies in
$n \in I_y$
, we conclude from equation (5.9) that the right-hand side of equation (5.19) lies in
![]() $[y, y^\alpha ]$
; from equations (5.18) and (1.5), we also see that this right-hand side is a odd integer. Since
$[y, y^\alpha ]$
; from equations (5.18) and (1.5), we also see that this right-hand side is a odd integer. Since
![]() $\mathbf {N}_y \equiv \mathbf {Log}( 2\mathbb {N}+1 \cap [y,y^\alpha ] )$
and
$\mathbf {N}_y \equiv \mathbf {Log}( 2\mathbb {N}+1 \cap [y,y^\alpha ] )$
and
 $$ \begin{align*}\sum_{N \in 2\mathbb{N}+1 \cap [y,y^\alpha]} \frac{1}{N} = \left(1 + O\left( \frac{1}{x}\right)\right) \frac{\alpha-1}{2} \log y,\end{align*} $$
$$ \begin{align*}\sum_{N \in 2\mathbb{N}+1 \cap [y,y^\alpha]} \frac{1}{N} = \left(1 + O\left( \frac{1}{x}\right)\right) \frac{\alpha-1}{2} \log y,\end{align*} $$
we thus see that when equation (5.18) occurs, one has
 $$ \begin{align*}\mathbb{P}( {\operatorname{Aff}}_{\vec a}(\mathbf{N}_y) = M ) = \frac{1}{\left(1 + O( \frac{1}{x})\right)\frac{\alpha-1}{2} \log y} 2^{-|\vec a|} \frac{3^{n-m_0}}{M - F_{n-m_0}(\vec a)}.\end{align*} $$
$$ \begin{align*}\mathbb{P}( {\operatorname{Aff}}_{\vec a}(\mathbf{N}_y) = M ) = \frac{1}{\left(1 + O( \frac{1}{x})\right)\frac{\alpha-1}{2} \log y} 2^{-|\vec a|} \frac{3^{n-m_0}}{M - F_{n-m_0}(\vec a)}.\end{align*} $$
From equations (5.10), (5.1) and (1.13), we can write
and thus
 $$ \begin{align*}\mathbb{P}( {\operatorname{Aff}}_{\vec a}(\mathbf{N}_y) = M ) = \frac{1 + O(x^{-c})}{\frac{\alpha-1}{2} \log y} \frac{2^{-|\vec a|} 3^{n-m_0}}{M}.\end{align*} $$
$$ \begin{align*}\mathbb{P}( {\operatorname{Aff}}_{\vec a}(\mathbf{N}_y) = M ) = \frac{1 + O(x^{-c})}{\frac{\alpha-1}{2} \log y} \frac{2^{-|\vec a|} 3^{n-m_0}}{M}.\end{align*} $$
We conclude that
 $$ \begin{align*} \mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) &= \frac{1 + O(x^{-c})}{\frac{\alpha-1}{2} \log y} \sum_{n \in I_y} 3^{n-m_0} \sum_{\vec a \in {\mathcal A}^{(n-m_0)}} 2^{-|\vec a|} \sum_{M \in E': M = F_{n-m_0}(\vec a) \bmod 3^{n-m_0}} \frac{1}{M} \\ &\quad + O( \log^{-c} x ). \end{align*} $$
$$ \begin{align*} \mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) &= \frac{1 + O(x^{-c})}{\frac{\alpha-1}{2} \log y} \sum_{n \in I_y} 3^{n-m_0} \sum_{\vec a \in {\mathcal A}^{(n-m_0)}} 2^{-|\vec a|} \sum_{M \in E': M = F_{n-m_0}(\vec a) \bmod 3^{n-m_0}} \frac{1}{M} \\ &\quad + O( \log^{-c} x ). \end{align*} $$
We will eventually establish the estimate
 $$ \begin{align} 3^{n-m_0} \sum_{\vec a \in {\mathcal A}^{(n-m_0)}} 2^{-|\vec a|} \sum_{M \in E': M = F_{n-m_0}(\vec a) \bmod 3^{n-m_0}} \frac{1}{M} = Z + O( \log^{-c} x ) \end{align} $$
$$ \begin{align} 3^{n-m_0} \sum_{\vec a \in {\mathcal A}^{(n-m_0)}} 2^{-|\vec a|} \sum_{M \in E': M = F_{n-m_0}(\vec a) \bmod 3^{n-m_0}} \frac{1}{M} = Z + O( \log^{-c} x ) \end{align} $$
for all
![]() $n \in I_y$
, where Z is the quantity
$n \in I_y$
, where Z is the quantity
 $$ \begin{align} Z := \sum_{M \in E'} \frac{3^{m_0} \mathbb{P}( M = \mathbf{Syrac}(\mathbb{Z}/3^{m_0}\mathbb{Z}) \bmod 3^{m_0})}{M}. \end{align} $$
$$ \begin{align} Z := \sum_{M \in E'} \frac{3^{m_0} \mathbb{P}( M = \mathbf{Syrac}(\mathbb{Z}/3^{m_0}\mathbb{Z}) \bmod 3^{m_0})}{M}. \end{align} $$
Since from equation (5.9), we have
 $$ \begin{align*}\# I_y = (1 + O( \log^{-c} x )) \frac{\alpha-1}{\log \frac{4}{3}} \log y,\end{align*} $$
$$ \begin{align*}\# I_y = (1 + O( \log^{-c} x )) \frac{\alpha-1}{\log \frac{4}{3}} \log y,\end{align*} $$
we see that equation (5.20) would imply the bound
 $$ \begin{align*}\mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = (1 + O(\log^{-c} x)) \frac{2}{\log \frac{4}{3}} Z + O(\log^{-c} x)\end{align*} $$
$$ \begin{align*}\mathbb{P}( {\operatorname{Pass}}_x( \mathbf{N}_y ) \in E ) = (1 + O(\log^{-c} x)) \frac{2}{\log \frac{4}{3}} Z + O(\log^{-c} x)\end{align*} $$
which would give the desired estimate in equation (5.7) since Z does not depend on whether y is equal to
![]() $x^\alpha $
or
$x^\alpha $
or
![]() $x^{\alpha ^2}$
.
$x^{\alpha ^2}$
.
It remains to establish equation (5.20). Fix
![]() $n \in I_y$
. The left-hand side of equation (5.20) may be written as
$n \in I_y$
. The left-hand side of equation (5.20) may be written as
where
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_{n-m_0}) \equiv \mathbf {Geom}(2)^{n-m_0}$
and
$(\mathbf {a}_1,\dots ,\mathbf {a}_{n-m_0}) \equiv \mathbf {Geom}(2)^{n-m_0}$
and
![]() $c_n\colon \mathbb {Z}/3^{n-m_0}\mathbb {Z} \to \mathbb {R}^+$
is the function
$c_n\colon \mathbb {Z}/3^{n-m_0}\mathbb {Z} \to \mathbb {R}^+$
is the function
 $$ \begin{align} c_n( X ) := 3^{n-m_0} \sum_{M \in E': M = X \bmod 3^{n-m_0}} \frac{1}{M}. \end{align} $$
$$ \begin{align} c_n( X ) := 3^{n-m_0} \sum_{M \in E': M = X \bmod 3^{n-m_0}} \frac{1}{M}. \end{align} $$
We have a basic estimate:
Lemma 5.3. We have
![]() $c_n(X) \ll 1$
for all
$c_n(X) \ll 1$
for all
![]() $n \in I_y$
and
$n \in I_y$
and
![]() $X \in \mathbb {Z}/3^{n-m_0}\mathbb {Z}$
.
$X \in \mathbb {Z}/3^{n-m_0}\mathbb {Z}$
.
Proof. We can split
 $$ \begin{align*}c_n(X) \leq \sum_{(a_1,\dots,a_{m_0}) \in \mathbb{N}^{m_0}} c_{n,a_1,\dots,a_{m_0}}(X),\end{align*} $$
$$ \begin{align*}c_n(X) \leq \sum_{(a_1,\dots,a_{m_0}) \in \mathbb{N}^{m_0}} c_{n,a_1,\dots,a_{m_0}}(X),\end{align*} $$
where
 $$ \begin{align*}c_{n,a_1,\dots,a_{m_0}}(X) := 3^{n-m_0} \sum_{M \in E': M = X \bmod 3^{n-m_0}; (a_1,\dots,a_{m_0}) := \vec a^{(m_0)}(M)} \frac{1}{M}.\end{align*} $$
$$ \begin{align*}c_{n,a_1,\dots,a_{m_0}}(X) := 3^{n-m_0} \sum_{M \in E': M = X \bmod 3^{n-m_0}; (a_1,\dots,a_{m_0}) := \vec a^{(m_0)}(M)} \frac{1}{M}.\end{align*} $$
We now estimate
![]() $c_{n,a_1,\dots ,a_{m_0}}(X)$
for a given
$c_{n,a_1,\dots ,a_{m_0}}(X)$
for a given
![]() $(a_1,\dots ,a_{m_0}) \in \mathbb {N}^{m_0}$
. If
$(a_1,\dots ,a_{m_0}) \in \mathbb {N}^{m_0}$
. If
![]() $M \in E'$
, then on setting
$M \in E'$
, then on setting
![]() $(a_1,\dots ,a_{m_0}) := \vec a^{(m_0)}(M)$
, we see from equation (1.7) that
$(a_1,\dots ,a_{m_0}) := \vec a^{(m_0)}(M)$
, we see from equation (1.7) that
which by equations (5.2) and (1.13) implies that
or equivalently
Also, from equation (1.7), we have that
and so M is constrained to a single residue class modulo
![]() $2^{a_{[1,m_0]}+1}$
. In equation (5.23), we are also constraining M to a single residue class modulo
$2^{a_{[1,m_0]}+1}$
. In equation (5.23), we are also constraining M to a single residue class modulo
![]() $3^{n-m_0}$
; by the Chinese remainder theorem, these constraints can be combined into a single residue class modulo
$3^{n-m_0}$
; by the Chinese remainder theorem, these constraints can be combined into a single residue class modulo
![]() $2^{a_{[1,m_0]}+1} 3^{n-m_0}$
. Note from the integral test that
$2^{a_{[1,m_0]}+1} 3^{n-m_0}$
. Note from the integral test that
 $$ \begin{align} \sum_{M_0 \leq M \leq M_1: M = a \bmod q} \frac{1}{M} &\leq \frac{1}{M_0} + \sum_{M_0+q \leq M \leq M_1: M = a \bmod q} \frac{1}{M} \nonumber\\ &\leq \frac{1}{M_0} + \frac{1}{q} \int_{M_0}^{M_1} \frac{dt}{t} \nonumber\\ &= \frac{1}{M_0} + \frac{1}{q} \log \frac{M_1}{M_0} \end{align} $$
$$ \begin{align} \sum_{M_0 \leq M \leq M_1: M = a \bmod q} \frac{1}{M} &\leq \frac{1}{M_0} + \sum_{M_0+q \leq M \leq M_1: M = a \bmod q} \frac{1}{M} \nonumber\\ &\leq \frac{1}{M_0} + \frac{1}{q} \int_{M_0}^{M_1} \frac{dt}{t} \nonumber\\ &= \frac{1}{M_0} + \frac{1}{q} \log \frac{M_1}{M_0} \end{align} $$
for any
![]() $M_0 \leq M_1$
and any residue class
$M_0 \leq M_1$
and any residue class
![]() $a \bmod q$
. In particular, for
$a \bmod q$
. In particular, for
![]() $q \leq M_0$
, we have
$q \leq M_0$
, we have
 $$ \begin{align} \sum_{M_0 \leq M \leq M_1: M = a \bmod q} \frac{1}{M} \ll \frac{1}{q} \log O \left( \frac{M_1}{M_0} \right). \end{align} $$
$$ \begin{align} \sum_{M_0 \leq M \leq M_1: M = a \bmod q} \frac{1}{M} \ll \frac{1}{q} \log O \left( \frac{M_1}{M_0} \right). \end{align} $$
If
![]() $2^{a_{[1,m_0]}} \leq x^{0.5}$
(say), then the modulus
$2^{a_{[1,m_0]}} \leq x^{0.5}$
(say), then the modulus
![]() $2^{a_{[1,m_0]}+1} 3^{n-m_0}$
is much less than the lower bound on M in equation (5.24), and we can then use the integral test to bound
$2^{a_{[1,m_0]}+1} 3^{n-m_0}$
is much less than the lower bound on M in equation (5.24), and we can then use the integral test to bound
 $$ \begin{align*} c_{n,a_1,\dots,a_{m_0}}(X) & \ll 3^{n-m_0} (2^{a_{[1,m_0]}+1} 3^{n-m_0})^{-1} \log O \left( \frac{3^{-m_0} 2^{a_{[1,m_0]}} x}{3^{-m_0} 2^{a_{[1,m_0-1]}} x } \right)\\ &\ll 2^{-a_{[1,m_0]}} a_{m_0} \\ &\ll 2^{-a_{[1,m_0]}/2}. \end{align*} $$
$$ \begin{align*} c_{n,a_1,\dots,a_{m_0}}(X) & \ll 3^{n-m_0} (2^{a_{[1,m_0]}+1} 3^{n-m_0})^{-1} \log O \left( \frac{3^{-m_0} 2^{a_{[1,m_0]}} x}{3^{-m_0} 2^{a_{[1,m_0-1]}} x } \right)\\ &\ll 2^{-a_{[1,m_0]}} a_{m_0} \\ &\ll 2^{-a_{[1,m_0]}/2}. \end{align*} $$
Now suppose instead that
![]() $2^{a_{[1,m_0]}}> x^{0.5}$
; we recall from equation (1.7) that
$2^{a_{[1,m_0]}}> x^{0.5}$
; we recall from equation (1.7) that
so
(using equations (1.13) and (5.24) to handle the lower order term). Hence we we have the additional lower bound
Applying equation (5.25) with
![]() $M_0$
equal to the larger of the two lower bounds on M, we conclude that
$M_0$
equal to the larger of the two lower bounds on M, we conclude that
 $$ \begin{align*} c_{n,a_1,\dots,a_{m_0}}(X) & \ll \frac{3^{n-m_0}}{3^{-m_0} 2^{a_{[1,m_0]}}} + 3^{n-m_0} (2^{a_{[1,m_0]}+1} 3^{n-m_0})^{-1} \log O \left( \frac{3^{-m_0} 2^{a_{[1,m_0]}} x}{3^{-m_0} 2^{a_{[1,m_0-1]}} x } \right)\\ &\ll 3^n 2^{-a_{[1,m_0]}} + 2^{-a_{[1,m_0]}} a_{m_0}\\ &\ll 2^{-a_{[1,m_0]}/2} \end{align*} $$
$$ \begin{align*} c_{n,a_1,\dots,a_{m_0}}(X) & \ll \frac{3^{n-m_0}}{3^{-m_0} 2^{a_{[1,m_0]}}} + 3^{n-m_0} (2^{a_{[1,m_0]}+1} 3^{n-m_0})^{-1} \log O \left( \frac{3^{-m_0} 2^{a_{[1,m_0]}} x}{3^{-m_0} 2^{a_{[1,m_0-1]}} x } \right)\\ &\ll 3^n 2^{-a_{[1,m_0]}} + 2^{-a_{[1,m_0]}} a_{m_0}\\ &\ll 2^{-a_{[1,m_0]}/2} \end{align*} $$
since
![]() $2^{-a_{[1,m_0]}} \leq x^{-1/4} 2^{-a_{[1,m_0]}/2} \leq 3^{-n} 2^{-a_{[1,m_0]}/2}$
for
$2^{-a_{[1,m_0]}} \leq x^{-1/4} 2^{-a_{[1,m_0]}/2} \leq 3^{-n} 2^{-a_{[1,m_0]}/2}$
for
![]() $n \in I_y$
. Thus we have
$n \in I_y$
. Thus we have
 $$ \begin{align*}c_n(X) \ll \sum_{a_1,\dots,a_{m_0} \in \mathbb{N}} 2^{-a_{[1,m_0]}/2}\end{align*} $$
$$ \begin{align*}c_n(X) \ll \sum_{a_1,\dots,a_{m_0} \in \mathbb{N}} 2^{-a_{[1,m_0]}/2}\end{align*} $$
and the claim follows from summing the geometric series.
From the above lemma and equation (5.12), we may write equation (5.22) as
which by equation (1.22) is equal to
From equations (5.9) and (5.2), we have
![]() $n-m_0 \geq m_0$
. Applying Proposition 1.14, Lemma 5.3 and the triangle inequality, one can thus write the preceding expression as
$n-m_0 \geq m_0$
. Applying Proposition 1.14, Lemma 5.3 and the triangle inequality, one can thus write the preceding expression as
and the claim in equation (5.20) then follows from equation (5.23).
6 Reduction to Fourier decay bound
In this section, we derive Proposition 1.14 from Proposition 1.17. We first observe that to prove Proposition 1.14, it suffices to do so in the regime
(The main significance of the constant
![]() $0.9$
here is that it lies between
$0.9$
here is that it lies between
![]() $\frac {\log 3}{2\log 2} \approx 0.7925$
and
$\frac {\log 3}{2\log 2} \approx 0.7925$
and
![]() $1$
.) Indeed, once one has equation (1.26) in this regime, one also has from equation (1.23) that
$1$
.) Indeed, once one has equation (1.26) in this regime, one also has from equation (1.23) that
 $$ \begin{align*}\sum_{Y \in \mathbb{Z}/3^{n'}\mathbb{Z}} \left|3^{n-n'} \mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z}) = Y \bmod 3^n ) - 3^{m-n'} \mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z}) = Y \bmod 3^m ) \right| \ll_A m^{-A} \end{align*} $$
$$ \begin{align*}\sum_{Y \in \mathbb{Z}/3^{n'}\mathbb{Z}} \left|3^{n-n'} \mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z}) = Y \bmod 3^n ) - 3^{m-n'} \mathbb{P}( \mathbf{Syrac}(\mathbb{Z}/3^n\mathbb{Z}) = Y \bmod 3^m ) \right| \ll_A m^{-A} \end{align*} $$
whenever
![]() $0.9 n \leq m \leq n \leq n'$
, and the claim in equation (1.26) for general
$0.9 n \leq m \leq n \leq n'$
, and the claim in equation (1.26) for general
![]() $10 \leq m \leq n$
then follows from telescoping series, with the remaining cases
$10 \leq m \leq n$
then follows from telescoping series, with the remaining cases
![]() $1 \leq m < 10$
following trivially from the triangle inequality.
$1 \leq m < 10$
following trivially from the triangle inequality.
Henceforth we assume equation (6.1). We also fix
![]() $A>0$
, and let
$A>0$
, and let
![]() $C_A$
be a constant that is sufficiently large depending on A. We may assume that n (and hence m) are sufficiently large depending on
$C_A$
be a constant that is sufficiently large depending on A. We may assume that n (and hence m) are sufficiently large depending on
![]() $A,C_A$
, since the claim is trivial otherwise.
$A,C_A$
, since the claim is trivial otherwise.
Let
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_n) \equiv \mathbf {Geom}(2)^n$
, and define the random variable
$(\mathbf {a}_1,\dots ,\mathbf {a}_n) \equiv \mathbf {Geom}(2)^n$
, and define the random variable
thus
![]() $\mathbf {X}_n \equiv \mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
. The strategy will be to split
$\mathbf {X}_n \equiv \mathbf {Syrac}(\mathbb {Z}/3^n\mathbb {Z})$
. The strategy will be to split
![]() $\mathbf {X}_n$
(after some conditioning and removal of exceptional events) as the sum of two independent components, one of which has quite large entropy (or more precisely, Renyi
$\mathbf {X}_n$
(after some conditioning and removal of exceptional events) as the sum of two independent components, one of which has quite large entropy (or more precisely, Renyi
![]() $2$
-entropy) in
$2$
-entropy) in
![]() $\mathbb {Z}/3^n\mathbb {Z}$
thanks to some elementary number theory, and the other having very small Fourier coefficients at high frequencies thanks to Proposition 1.17. The desired bound will then follow from some
$\mathbb {Z}/3^n\mathbb {Z}$
thanks to some elementary number theory, and the other having very small Fourier coefficients at high frequencies thanks to Proposition 1.17. The desired bound will then follow from some
![]() $L^2$
-based Fourier analysis (i.e., Plancherel’s theorem).
$L^2$
-based Fourier analysis (i.e., Plancherel’s theorem).
We turn to the details. Let E denote the event that the inequalities
hold for every
![]() $1 \leq i \leq j \leq n$
. The event E occurs with nearly full probability; indeed, from Lemma 2.2 and the union bound, we can bound the probability of the complementary event
$1 \leq i \leq j \leq n$
. The event E occurs with nearly full probability; indeed, from Lemma 2.2 and the union bound, we can bound the probability of the complementary event
![]() $\overline {E}$
by
$\overline {E}$
by
 $$ \begin{align} \mathbb{P}( \overline{E}) &\ll \sum_{1 \leq i \leq j \leq n} G_{j-i}( c C_A ( \sqrt{(j-i)(\log n)} + \log n ) ) \nonumber\\ &\ll \sum_{1 \leq i \leq j \leq n} \exp( - c C_A \log n ) + \exp( - c C_A \log n) \nonumber\\ &\ll n^2 n^{-c C_A} \nonumber\\ &\ll n^{-A-1} \end{align} $$
$$ \begin{align} \mathbb{P}( \overline{E}) &\ll \sum_{1 \leq i \leq j \leq n} G_{j-i}( c C_A ( \sqrt{(j-i)(\log n)} + \log n ) ) \nonumber\\ &\ll \sum_{1 \leq i \leq j \leq n} \exp( - c C_A \log n ) + \exp( - c C_A \log n) \nonumber\\ &\ll n^2 n^{-c C_A} \nonumber\\ &\ll n^{-A-1} \end{align} $$
if
![]() $C_A$
is large enough. By the triangle inequality, we may then bound the left-hand side of equation (1.26) by
$C_A$
is large enough. By the triangle inequality, we may then bound the left-hand side of equation (1.26) by
so it now suffices to show that
Now suppose that E holds. From equation (6.2), we have
since
![]() $\frac {\log 3}{\log 2} < 2$
and n is large. Thus, there is a well-defined stopping time
$\frac {\log 3}{\log 2} < 2$
and n is large. Thus, there is a well-defined stopping time
![]() $0 \leq \mathbf {k} < n$
, defined as the unique natural number
$0 \leq \mathbf {k} < n$
, defined as the unique natural number
![]() $\mathbf {k}$
for which
$\mathbf {k}$
for which
From equation (6.2), we have
It thus suffices by the union bound to show that
for all
where
![]() $B_k$
is the event that
$B_k$
is the event that
![]() $\mathbf {k}=k$
, or equivalently that
$\mathbf {k}=k$
, or equivalently that
Fix k. In order to decouple the events involved in equation (6.4), we need to enlarge the event E slightly, so that it only depends on
![]() $\mathbf {a}_1,\dots ,\mathbf {a}_{k+1}$
and not on
$\mathbf {a}_1,\dots ,\mathbf {a}_{k+1}$
and not on
![]() $\mathbf {a}_{k+2},\dots ,\mathbf {a}_n$
. Let
$\mathbf {a}_{k+2},\dots ,\mathbf {a}_n$
. Let
![]() $E_k$
denote the event that the inequalities in equation (6.2) hold for
$E_k$
denote the event that the inequalities in equation (6.2) hold for
![]() $1 \leq i < j \leq k+1$
; thus
$1 \leq i < j \leq k+1$
; thus
![]() $E_k$
contains E. Then the difference between E and
$E_k$
contains E. Then the difference between E and
![]() $E_k$
has probability
$E_k$
has probability
![]() $O(n^{-A-1})$
by in equation (6.3). Thus by the triangle inequality, the estimate in equation (6.4) is equivalent to
$O(n^{-A-1})$
by in equation (6.3). Thus by the triangle inequality, the estimate in equation (6.4) is equivalent to
From equations (6.6) and (6.2), we see that we have
whenever one is in the event
![]() $E_k \wedge B_k$
. By a further application of the triangle inequality, it suffices to show that
$E_k \wedge B_k$
. By a further application of the triangle inequality, it suffices to show that
for all l in the range
where
![]() $C_{k,l}$
is the event that
$C_{k,l}$
is the event that
![]() $\mathbf {a}_{[1,k+1]}=l$
.
$\mathbf {a}_{[1,k+1]}=l$
.
Fix l. If we let
![]() $g = g_{n,k,l}\colon \mathbb {Z}/3^n\mathbb {Z} \to \mathbb {R}$
denote the function
$g = g_{n,k,l}\colon \mathbb {Z}/3^n\mathbb {Z} \to \mathbb {R}$
denote the function
then our task can be written as
 $$ \begin{align*}\sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} \left|g(Y) - \frac{1}{3^{n-m}} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} g(Y') \right| \ll_{A,C_A} n^{-A-2}.\end{align*} $$
$$ \begin{align*}\sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} \left|g(Y) - \frac{1}{3^{n-m}} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} g(Y') \right| \ll_{A,C_A} n^{-A-2}.\end{align*} $$
By Cauchy-Schwarz, it suffices to show that
 $$ \begin{align} 3^{n} \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} \left|g(Y) - \frac{1}{3^{n-m}} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} g(Y') \right|{}^2 \ll_{A,C_A} n^{-2A-4}. \end{align} $$
$$ \begin{align} 3^{n} \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} \left|g(Y) - \frac{1}{3^{n-m}} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} g(Y') \right|{}^2 \ll_{A,C_A} n^{-2A-4}. \end{align} $$
By the Fourier inversion formula, we have
 $$ \begin{align*}g(Y) = 3^{-n} \sum_{\xi \in \mathbb{Z}/3^n\mathbb{Z}} \left( \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}} g(Y') e^{-2\pi i \xi Y' / 3^n} \right) e^{2\pi i \xi Y/3^n}\end{align*} $$
$$ \begin{align*}g(Y) = 3^{-n} \sum_{\xi \in \mathbb{Z}/3^n\mathbb{Z}} \left( \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}} g(Y') e^{-2\pi i \xi Y' / 3^n} \right) e^{2\pi i \xi Y/3^n}\end{align*} $$
and
 $$ \begin{align*}\frac{1}{3^{n-m}} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} g(Y') = 3^{-n} \sum_{\xi \in 3^{n-m}\mathbb{Z}/3^n\mathbb{Z}} \left( \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}} g(Y') e^{-2\pi i \xi Y' / 3^n} \right) e^{2\pi i \xi Y/3^n}\end{align*} $$
$$ \begin{align*}\frac{1}{3^{n-m}} \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}: Y' = Y \bmod 3^m} g(Y') = 3^{-n} \sum_{\xi \in 3^{n-m}\mathbb{Z}/3^n\mathbb{Z}} \left( \sum_{Y' \in \mathbb{Z}/3^n\mathbb{Z}} g(Y') e^{-2\pi i \xi Y' / 3^n} \right) e^{2\pi i \xi Y/3^n}\end{align*} $$
for any
![]() $Y \in \mathbb {Z}/3^n\mathbb {Z}$
, so by Plancherel’s theorem, the left-hand side of equation (6.10) may be written as
$Y \in \mathbb {Z}/3^n\mathbb {Z}$
, so by Plancherel’s theorem, the left-hand side of equation (6.10) may be written as
 $$ \begin{align*}\sum_{\xi \in \mathbb{Z}/3^n\mathbb{Z}: \xi \not \in 3^{n-m}\mathbb{Z}/3^n\mathbb{Z}} \left| \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} g(Y) e^{-2\pi i \xi Y / 3^n} \right|{}^2.\end{align*} $$
$$ \begin{align*}\sum_{\xi \in \mathbb{Z}/3^n\mathbb{Z}: \xi \not \in 3^{n-m}\mathbb{Z}/3^n\mathbb{Z}} \left| \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} g(Y) e^{-2\pi i \xi Y / 3^n} \right|{}^2.\end{align*} $$
By equation (6.9), we can write
On the event
![]() $C_{k,l}$
, one can use equations (1.5) and (1.29) to write
$C_{k,l}$
, one can use equations (1.5) and (1.29) to write
The key point here is that the random variable
![]() $3^{k+1} 2^{-l} F_{n-k-1}(\mathbf {a}_n,\dots ,\mathbf {a}_{k+2})$
is independent of
$3^{k+1} 2^{-l} F_{n-k-1}(\mathbf {a}_n,\dots ,\mathbf {a}_{k+2})$
is independent of
![]() $\mathbf {a}_1,\dots ,\mathbf {a}_{k+1}, E_k, B_k, C_{k,l}$
. Thus we may factor
$\mathbf {a}_1,\dots ,\mathbf {a}_{k+1}, E_k, B_k, C_{k,l}$
. Thus we may factor
 $$ \begin{align*} \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} g(Y) e^{-2\pi i \xi Y / 3^n} &= \mathbb{E} e^{-2\pi i \xi (F_{k+1}(\mathbf{a}_{k+1},\dots,\mathbf{a}_1) \bmod 3^n) / 3^n} 1_{E_k \wedge B_k \wedge C_{k,l}} \\ &\quad \times \mathbb{E} e^{-2\pi i \xi (2^{-l} F_{n-k-1}(\mathbf{a}_n,\dots,\mathbf{a}_{k+2}) \bmod 3^{n-k-1}) / 3^{n-k-1}}. \end{align*} $$
$$ \begin{align*} \sum_{Y \in \mathbb{Z}/3^n\mathbb{Z}} g(Y) e^{-2\pi i \xi Y / 3^n} &= \mathbb{E} e^{-2\pi i \xi (F_{k+1}(\mathbf{a}_{k+1},\dots,\mathbf{a}_1) \bmod 3^n) / 3^n} 1_{E_k \wedge B_k \wedge C_{k,l}} \\ &\quad \times \mathbb{E} e^{-2\pi i \xi (2^{-l} F_{n-k-1}(\mathbf{a}_n,\dots,\mathbf{a}_{k+2}) \bmod 3^{n-k-1}) / 3^{n-k-1}}. \end{align*} $$
For
![]() $\xi $
in
$\xi $
in
![]() $\mathbb {Z}/3^n\mathbb {Z}$
that does not lie in
$\mathbb {Z}/3^n\mathbb {Z}$
that does not lie in
![]() $3^{n-m}\mathbb {Z}/3^n\mathbb {Z}$
, we can write
$3^{n-m}\mathbb {Z}/3^n\mathbb {Z}$
, we can write
![]() $\xi = 3^j 2^l \xi ' \bmod 3^n$
, where
$\xi = 3^j 2^l \xi ' \bmod 3^n$
, where
![]() $0 \leq j < n-m \leq 0.1 n$
and
$0 \leq j < n-m \leq 0.1 n$
and
![]() $\xi '$
is not divisible by
$\xi '$
is not divisible by
![]() $3$
. In particular, from equation (6.5), one has
$3$
. In particular, from equation (6.5), one has
Then by equation (1.23), we have
and hence by Proposition 1.17 this quantity is
![]() $O_{A'}(n^{-A'})$
for any
$O_{A'}(n^{-A'})$
for any
![]() $A'$
. Thus we can bound the left-hand side of equation (6.10) by
$A'$
. Thus we can bound the left-hand side of equation (6.10) by
 $$ \begin{align} \ll_{A'} n^{-2 A'} \sum_{\xi \in \mathbb{Z}/3^n\mathbb{Z}} \left|\mathbb{E} e^{-2\pi i \xi (F_{k+1}(\mathbf{a}_{k+1},\dots,\mathbf{a}_1) \bmod 3^n) / 3^n} 1_{\overline{E}_k \wedge B_k \wedge C_{k,l}} \right|{}^2 \end{align} $$
$$ \begin{align} \ll_{A'} n^{-2 A'} \sum_{\xi \in \mathbb{Z}/3^n\mathbb{Z}} \left|\mathbb{E} e^{-2\pi i \xi (F_{k+1}(\mathbf{a}_{k+1},\dots,\mathbf{a}_1) \bmod 3^n) / 3^n} 1_{\overline{E}_k \wedge B_k \wedge C_{k,l}} \right|{}^2 \end{align} $$
(where we have now discarded the restriction
![]() $\xi \not \in 3^{n-m}\mathbb {Z}/3^n\mathbb {Z}$
); by Plancherel’s theorem, this expression can be written as
$\xi \not \in 3^{n-m}\mathbb {Z}/3^n\mathbb {Z}$
); by Plancherel’s theorem, this expression can be written as
Remark 6.1. If we ignore the technical restriction to the events
![]() $E_k, B_k, C_{k,l}$
, this quantity is essentially the Renyi
$E_k, B_k, C_{k,l}$
, this quantity is essentially the Renyi
![]() $2$
-entropy (also known as collision entropy) of the random variable
$2$
-entropy (also known as collision entropy) of the random variable
![]() $F_{k+1}(\mathbf {a}_{k+1},\dots ,\mathbf {a}_1) \bmod 3^n$
.
$F_{k+1}(\mathbf {a}_{k+1},\dots ,\mathbf {a}_1) \bmod 3^n$
.
Now we make a key elementary number theory observation:
Lemma 6.2 (Injectivity of offsets)
For each natural number n, the n-Syracuse offset map
![]() $F_n\colon (\mathbb {N}+1)^n \to \mathbb {Z}[\frac {1}{2}]$
is injective.
$F_n\colon (\mathbb {N}+1)^n \to \mathbb {Z}[\frac {1}{2}]$
is injective.
Proof. Suppose that
![]() $(a_1,\dots ,a_n), (a^{\prime }_1,\dots ,a^{\prime }_n) \in (\mathbb {N}+1)^n$
are such that
$(a_1,\dots ,a_n), (a^{\prime }_1,\dots ,a^{\prime }_n) \in (\mathbb {N}+1)^n$
are such that
![]() $F_n(a_1,\dots ,a_n) = F_n(a^{\prime }_1,\dots ,a^{\prime }_n)$
. Taking
$F_n(a_1,\dots ,a_n) = F_n(a^{\prime }_1,\dots ,a^{\prime }_n)$
. Taking
![]() $2$
-valuations of both sides using equation (1.5), we conclude that
$2$
-valuations of both sides using equation (1.5), we conclude that
On the other hand, from equation (1.5), we have
and similarly for
![]() $a^{\prime }_1,\dots ,a^{\prime }_n$
, hence
$a^{\prime }_1,\dots ,a^{\prime }_n$
, hence
The claim now follows from iteration (or an induction on n).
We will need a more quantitative
![]() $3$
-adic version of this injectivity:
$3$
-adic version of this injectivity:
Corollary 6.3
 $3$
-adic separation of offsets
$3$
-adic separation of offsets
Let
![]() $C_A$
be sufficiently large, let n be sufficiently large (depending on
$C_A$
be sufficiently large, let n be sufficiently large (depending on
![]() $C_A$
), let k be a natural number, and let l be a natural number obeying equation (6.8). Then the residue classes
$C_A$
), let k be a natural number, and let l be a natural number obeying equation (6.8). Then the residue classes
![]() $F_{k+1}(a_{k+1},\dots ,a_1) \bmod 3^n$
, as
$F_{k+1}(a_{k+1},\dots ,a_1) \bmod 3^n$
, as
![]() $(a_1,\dots ,a_{k+1}) \in (\mathbb {N}+1)^{k+1}$
range over
$(a_1,\dots ,a_{k+1}) \in (\mathbb {N}+1)^{k+1}$
range over
![]() ${k+1}$
-tuples of positive integers that obey the conditions
${k+1}$
-tuples of positive integers that obey the conditions
for
![]() $1 \leq i < j \leq k+1$
as well as
$1 \leq i < j \leq k+1$
as well as
are distinct.
Proof. Suppose that
![]() $(a_1,\dots ,a_{k+1}), (a^{\prime }_1,\dots ,a^{\prime }_{k+1})$
are two tuples of positive integers that both obey equations (6.12) and (6.13), and such that
$(a_1,\dots ,a_{k+1}), (a^{\prime }_1,\dots ,a^{\prime }_{k+1})$
are two tuples of positive integers that both obey equations (6.12) and (6.13), and such that
Applying equation (1.5) and multiplying by
![]() $2^l$
, we conclude that
$2^l$
, we conclude that
 $$ \begin{align} \sum_{j=1}^{k+1} 3^{j-1} 2^{l - a_{[1,j]}} = \sum_{j=1}^{k+1} 3^{j-1} 2^{l - a^{\prime}_{[1,j]}} \bmod 3^n. \end{align} $$
$$ \begin{align} \sum_{j=1}^{k+1} 3^{j-1} 2^{l - a_{[1,j]}} = \sum_{j=1}^{k+1} 3^{j-1} 2^{l - a^{\prime}_{[1,j]}} \bmod 3^n. \end{align} $$
From equation (6.13), the expressions on the left and right sides are natural numbers. Using equations (6.12) and (6.8), and Young’s inequality
![]() $C_A j^{1/2} \log ^{1/2} n \leq \frac {\varepsilon }{2} j + \frac {1}{2\varepsilon } C_A^2 \log n$
for a sufficiently small
$C_A j^{1/2} \log ^{1/2} n \leq \frac {\varepsilon }{2} j + \frac {1}{2\varepsilon } C_A^2 \log n$
for a sufficiently small
![]() $\varepsilon>0$
, the left-hand side may be bounded for
$\varepsilon>0$
, the left-hand side may be bounded for
![]() $C_A$
large enough by
$C_A$
large enough by
 $$ \begin{align*} \sum_{j=1}^{k+1} 3^{j-1} 2^{l - a_{[1,j]}} &\ll 2^l \sum_{j=1}^{k+1} 3^{j} 2^{- 2j + C_A (\sqrt{j \log n} + \log n)} \\ &\ll \exp( - \frac{(C_A)^2}{2} \log n ) 3^n \sum_{j=1}^{k+1} \exp\left( - j \log \frac{4}{3} + O( C_A j^{1/2} \log^{1/2} n ) + O( C_A \log n ) \right) \\ &\ll \exp\left( - \frac{(C_A)^2}{4} \log n \right) 3^n \sum_{j=1}^{k+1} \exp( - c j ) \\ &\ll n^{- \frac{(C_A)^2}{4}} 3^n; \end{align*} $$
$$ \begin{align*} \sum_{j=1}^{k+1} 3^{j-1} 2^{l - a_{[1,j]}} &\ll 2^l \sum_{j=1}^{k+1} 3^{j} 2^{- 2j + C_A (\sqrt{j \log n} + \log n)} \\ &\ll \exp( - \frac{(C_A)^2}{2} \log n ) 3^n \sum_{j=1}^{k+1} \exp\left( - j \log \frac{4}{3} + O( C_A j^{1/2} \log^{1/2} n ) + O( C_A \log n ) \right) \\ &\ll \exp\left( - \frac{(C_A)^2}{4} \log n \right) 3^n \sum_{j=1}^{k+1} \exp( - c j ) \\ &\ll n^{- \frac{(C_A)^2}{4}} 3^n; \end{align*} $$
in particular, for n large enough, this expression is less than
![]() $3^n$
. Similarly for the right-hand side of equation (6.14). Thus these two sides are equal as natural numbers, not simply as residue classes modulo
$3^n$
. Similarly for the right-hand side of equation (6.14). Thus these two sides are equal as natural numbers, not simply as residue classes modulo
![]() $3^n$
:
$3^n$
:
 $$ \begin{align} \sum_{j=1}^{k+1} 3^{j-1} 2^{l-a_{[1,j]}} = \sum_{j=1}^{k+1} 3^{j-1} 2^{l-a^{\prime}_{[1,j]}}. \end{align} $$
$$ \begin{align} \sum_{j=1}^{k+1} 3^{j-1} 2^{l-a_{[1,j]}} = \sum_{j=1}^{k+1} 3^{j-1} 2^{l-a^{\prime}_{[1,j]}}. \end{align} $$
Dividing by
![]() $2^l$
, we conclude
$2^l$
, we conclude
![]() $F_{k+1}(a_{k+1},\dots ,a_1) = F_{k+1}(a^{\prime }_{k+1},\dots ,a^{\prime }_1)$
. From Lemma 6.2, we conclude that
$F_{k+1}(a_{k+1},\dots ,a_1) = F_{k+1}(a^{\prime }_{k+1},\dots ,a^{\prime }_1)$
. From Lemma 6.2, we conclude that
![]() $(a_1,\dots ,a_{k+1}) = (a^{\prime }_1,\dots ,a^{\prime }_{k+1})$
, and the claim follows.
$(a_1,\dots ,a_{k+1}) = (a^{\prime }_1,\dots ,a^{\prime }_{k+1})$
, and the claim follows.
In view of the above lemma, we see that for a given choice of
![]() $Y_{k+1} \in \mathbb {Z}/3^n\mathbb {Z}$
, the event
$Y_{k+1} \in \mathbb {Z}/3^n\mathbb {Z}$
, the event
can only be non-empty for at most one value
![]() $(a_1,\dots ,a_{m})$
of the tuple
$(a_1,\dots ,a_{m})$
of the tuple
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_{m})$
. By Definition 1.7, such a value is attained with probability
$(\mathbf {a}_1,\dots ,\mathbf {a}_{m})$
. By Definition 1.7, such a value is attained with probability
![]() $2^{-a_{[1,m]}} = 2^{-l}$
, which by equation (6.8) is equal to
$2^{-a_{[1,m]}} = 2^{-l}$
, which by equation (6.8) is equal to
![]() $n^{O((C_A)^2)} 3^{-n}$
. We can thus bound equation (6.11) (and hence the left-hand side of equation (6.10)) by
$n^{O((C_A)^2)} 3^{-n}$
. We can thus bound equation (6.11) (and hence the left-hand side of equation (6.10)) by
and the claim now follows by taking
![]() $A'$
large enough. This concludes the proof of Proposition 1.14 assuming Proposition 1.17.
$A'$
large enough. This concludes the proof of Proposition 1.14 assuming Proposition 1.17.
7 Decay of Fourier coefficients
In this section, we establish Proposition 1.17, which, when combined with all the implications established in preceding sections, will yield Theorem 1.3.
Let
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $\xi \in \mathbb {Z}/3^n\mathbb {Z}$
be not divisible by
$\xi \in \mathbb {Z}/3^n\mathbb {Z}$
be not divisible by
![]() $3$
, and let
$3$
, and let
![]() $A>0$
be fixed. We will not vary n or
$A>0$
be fixed. We will not vary n or
![]() $\xi $
in this argument, but it is important that all of our estimates are uniform in these parameters. Without loss of generality we may assume A to be larger than any fixed absolute constant. We let
$\xi $
in this argument, but it is important that all of our estimates are uniform in these parameters. Without loss of generality we may assume A to be larger than any fixed absolute constant. We let
![]() $\chi = \chi _{n,\xi } \colon \mathbb {Z}[\frac {1}{2}] \to \mathbb {C}$
denote the character
$\chi = \chi _{n,\xi } \colon \mathbb {Z}[\frac {1}{2}] \to \mathbb {C}$
denote the character
where
![]() $x \mapsto x \bmod 3^n$
is the ring homomorphism from
$x \mapsto x \bmod 3^n$
is the ring homomorphism from
![]() $\mathbb {Z}[\frac {1}{2}]$
to
$\mathbb {Z}[\frac {1}{2}]$
to
![]() $\mathbb {Z}/3^n\mathbb {Z}$
(mapping
$\mathbb {Z}/3^n\mathbb {Z}$
(mapping
![]() $\frac {1}{2}$
to
$\frac {1}{2}$
to
![]() $\frac {1}{2} \bmod 3^n = \frac {3^n+1}{2} \bmod 3^n$
). Note that
$\frac {1}{2} \bmod 3^n = \frac {3^n+1}{2} \bmod 3^n$
). Note that
![]() $\chi $
is a group homomorphism from the additive group
$\chi $
is a group homomorphism from the additive group
![]() $\mathbb {Z}[\frac {1}{2}]$
to the multiplicative group
$\mathbb {Z}[\frac {1}{2}]$
to the multiplicative group
![]() $\mathbb {C}$
, which is periodic modulo
$\mathbb {C}$
, which is periodic modulo
![]() $3^n$
, so it also descends to a group homomorphism from
$3^n$
, so it also descends to a group homomorphism from
![]() $\mathbb {Z}/3^n\mathbb {Z}$
to
$\mathbb {Z}/3^n\mathbb {Z}$
to
![]() $\mathbb {C}$
, which is still defined by the same formula in equation equation (7.1). From equation (1.29), our task now reducesFootnote
7
to establishing the following claim.
$\mathbb {C}$
, which is still defined by the same formula in equation equation (7.1). From equation (1.29), our task now reducesFootnote
7
to establishing the following claim.
Proposition 7.1 (Key Fourier decay estimate)
Let
![]() $\chi $
be defined by equation (7.1), and let
$\chi $
be defined by equation (7.1), and let
![]() $(\mathbf {a}_1,\dots ,\mathbf {a}_n) \equiv \mathbf {Geom}(2)^n$
be n iid copies of the geometric distribution
$(\mathbf {a}_1,\dots ,\mathbf {a}_n) \equiv \mathbf {Geom}(2)^n$
be n iid copies of the geometric distribution
![]() $\mathbf {Geom}(2)$
(as defined in Definition 1.7). Then the quantity
$\mathbf {Geom}(2)$
(as defined in Definition 1.7). Then the quantity
obeys the estimate
for any
![]() $A>0$
, where we use the summation convention
$A>0$
, where we use the summation convention
![]() $\mathbf {a}_{[i,j]} := \mathbf {a}_i + \dots + \mathbf {a}_j$
from equation (1.6).
$\mathbf {a}_{[i,j]} := \mathbf {a}_i + \dots + \mathbf {a}_j$
from equation (1.6).
7.1 Estimation in terms of white points
To extract some usable cancellation in the expression
![]() $S_\chi (n)$
, we will group the sum on the left-hand side into pairs. For any real
$S_\chi (n)$
, we will group the sum on the left-hand side into pairs. For any real
![]() $x>0$
, let
$x>0$
, let
![]() $[x]$
denote the discrete interval
$[x]$
denote the discrete interval
For
![]() $j \in [n/2]$
, set
$j \in [n/2]$
, set
![]() $\mathbf {b}_j := \mathbf {a}_{2j-1} + \mathbf {a}_{2j}$
, so that
$\mathbf {b}_j := \mathbf {a}_{2j-1} + \mathbf {a}_{2j}$
, so that
 $$ \begin{align*}2^{-\mathbf{a}_1} + 3^1 2^{-\mathbf{a}_{[1,2]}} + \dots + 3^{n-1} 2^{-\mathbf{a}_{[1,n]}} = \sum_{j \in [n/2]} 3^{2j-2} 2^{-\mathbf{b}_{[1,j]}} ( 2^{\mathbf{a}_{2j}} + 3 ) + 3^{n-1} 2^{-\mathbf{b}_{[1,\lfloor n/2\rfloor]}-\mathbf{a}_n}\end{align*} $$
$$ \begin{align*}2^{-\mathbf{a}_1} + 3^1 2^{-\mathbf{a}_{[1,2]}} + \dots + 3^{n-1} 2^{-\mathbf{a}_{[1,n]}} = \sum_{j \in [n/2]} 3^{2j-2} 2^{-\mathbf{b}_{[1,j]}} ( 2^{\mathbf{a}_{2j}} + 3 ) + 3^{n-1} 2^{-\mathbf{b}_{[1,\lfloor n/2\rfloor]}-\mathbf{a}_n}\end{align*} $$
when n is odd, where we extend the summation notation in equation (1.6) to the
![]() $\mathbf {b}_j$
. For n even, the formula is the same except that the final term
$\mathbf {b}_j$
. For n even, the formula is the same except that the final term
![]() $3^{n-1} 2^{-\mathbf {b}_{[1,\lfloor n/2\rfloor ]}-\mathbf {a}_n}$
is omitted. Note that the
$3^{n-1} 2^{-\mathbf {b}_{[1,\lfloor n/2\rfloor ]}-\mathbf {a}_n}$
is omitted. Note that the
![]() $\mathbf {b}_1,\dots ,\mathbf {b}_{\lfloor n/2\rfloor }$
are jointly independent random variables taking values in
$\mathbf {b}_1,\dots ,\mathbf {b}_{\lfloor n/2\rfloor }$
are jointly independent random variables taking values in
![]() $\mathbb {N}+2 = \{2,3,4,\dots \}$
; they are iid copies of a Pascal (or negative binomial) random variable
$\mathbb {N}+2 = \{2,3,4,\dots \}$
; they are iid copies of a Pascal (or negative binomial) random variable
![]() $\mathbf {Pascal} \equiv \mathbf {NB}(2,\frac {1}{2})$
on
$\mathbf {Pascal} \equiv \mathbf {NB}(2,\frac {1}{2})$
on
![]() $\mathbb {N}+2$
, defined by
$\mathbb {N}+2$
, defined by
for
![]() $b \in \mathbb {N}+2$
.
$b \in \mathbb {N}+2$
.
For any
![]() $j \in [n/2]$
,
$j \in [n/2]$
,
![]() $\mathbf {a}_{2j}$
is independent of all of the
$\mathbf {a}_{2j}$
is independent of all of the
![]() $\mathbf {b}_1,\dots ,\mathbf {b}_{\lfloor n/2\rfloor }$
except for
$\mathbf {b}_1,\dots ,\mathbf {b}_{\lfloor n/2\rfloor }$
except for
![]() $\mathbf {b}_j$
. For n odd,
$\mathbf {b}_j$
. For n odd,
![]() $\mathbf {a}_n$
is independent of all of the
$\mathbf {a}_n$
is independent of all of the
![]() $\mathbf {b}_j$
. Regardless of whether n is even or odd, once one conditions on all of the
$\mathbf {b}_j$
. Regardless of whether n is even or odd, once one conditions on all of the
![]() $\mathbf {b}_j$
to be fixed, the random variables
$\mathbf {b}_j$
to be fixed, the random variables
![]() $\mathbf {a}_{2j}, j \leq [n/2]$
(as well as
$\mathbf {a}_{2j}, j \leq [n/2]$
(as well as
![]() $\mathbf {a}_n$
, if n is odd) are all independent of each other. We conclude that
$\mathbf {a}_n$
, if n is odd) are all independent of each other. We conclude that
 $$ \begin{align*}S_\chi(n) = \mathbb{E} \left(\prod_{j \in [n/2]} f( 3^{2j-2} 2^{-\mathbf{b}_{[1,j]}}, \mathbf{b}_j )\right) g( 3^{n-1} 2^{-\mathbf{b}_{[1,\lfloor n/2\rfloor]}} )\end{align*} $$
$$ \begin{align*}S_\chi(n) = \mathbb{E} \left(\prod_{j \in [n/2]} f( 3^{2j-2} 2^{-\mathbf{b}_{[1,j]}}, \mathbf{b}_j )\right) g( 3^{n-1} 2^{-\mathbf{b}_{[1,\lfloor n/2\rfloor]}} )\end{align*} $$
when n is odd, with the factor
![]() $g( 2^{-\mathbf {b}_{[1,\lfloor n/2\rfloor ]}} )$
omitted when n is even, where
$g( 2^{-\mathbf {b}_{[1,\lfloor n/2\rfloor ]}} )$
omitted when n is even, where
![]() $f(x,b)$
is the conditional expectation
$f(x,b)$
is the conditional expectation
(with
![]() $(\mathbf {a}_1,\mathbf {a}_2) \equiv \mathbf {Geom}(2)^2$
) and
$(\mathbf {a}_1,\mathbf {a}_2) \equiv \mathbf {Geom}(2)^2$
) and
Clearly
![]() $|g(x)| \leq 1$
, so by the triangle inequality we can bound
$|g(x)| \leq 1$
, so by the triangle inequality we can bound
 $$ \begin{align} |S_\chi(n)| \leq \mathbb{E} \prod_{j \in [n/2]} |f( 3^{2j-2} 2^{-\mathbf{b}_{[1,j]}}, \mathbf{b}_j )| \end{align} $$
$$ \begin{align} |S_\chi(n)| \leq \mathbb{E} \prod_{j \in [n/2]} |f( 3^{2j-2} 2^{-\mathbf{b}_{[1,j]}}, \mathbf{b}_j )| \end{align} $$
regardless of whether n is even or odd.
From equation (7.4), we certainly have
We now perform an explicit computation to improve upon this estimate for many values of x (of the form
![]() $x = 3^{2j-2} 2^{-l}$
) in the case
$x = 3^{2j-2} 2^{-l}$
) in the case
![]() $b = 3$
, which is the least value of
$b = 3$
, which is the least value of
![]() $b \in \mathbb {N}+2$
for which the event
$b \in \mathbb {N}+2$
for which the event
![]() $\mathbf {a}_1+\mathbf {a}_2=b$
does not completely determine
$\mathbf {a}_1+\mathbf {a}_2=b$
does not completely determine
![]() $\mathbf {a}_1$
or
$\mathbf {a}_1$
or
![]() $\mathbf {a}_2$
. For any
$\mathbf {a}_2$
. For any
![]() $(j,l) \in (\mathbb {N}+1) \times \mathbb {Z}$
, we can write
$(j,l) \in (\mathbb {N}+1) \times \mathbb {Z}$
, we can write
where
![]() $\theta (j,l) = \theta _{n,\xi }(j,l) \in (-1/2,1/2]$
denotes the argument
$\theta (j,l) = \theta _{n,\xi }(j,l) \in (-1/2,1/2]$
denotes the argument
 $$ \begin{align} \theta(j,l) := \left\{ \frac{\xi 3^{2j-2} (2^{-l+1} \bmod 3^n)}{3^n} \right\} \end{align} $$
$$ \begin{align} \theta(j,l) := \left\{ \frac{\xi 3^{2j-2} (2^{-l+1} \bmod 3^n)}{3^n} \right\} \end{align} $$
and
![]() $\{\}\colon \mathbb {R}/\mathbb {Z} \to (-1/2,1/2]$
is the signed fractional part function; thus
$\{\}\colon \mathbb {R}/\mathbb {Z} \to (-1/2,1/2]$
is the signed fractional part function; thus
![]() $\{x\}$
denotes the unique element of the coset
$\{x\}$
denotes the unique element of the coset
![]() $x + \mathbb {Z}$
that lies in
$x + \mathbb {Z}$
that lies in
![]() $(-1/2,1/2]$
.
$(-1/2,1/2]$
.
Let
![]() $0 < \varepsilon < \frac {1}{100}$
be a sufficiently small absolute constant to be chosen later; we will take care to ensure that the implied constants in many of our asymptotic estimates do not depend on
$0 < \varepsilon < \frac {1}{100}$
be a sufficiently small absolute constant to be chosen later; we will take care to ensure that the implied constants in many of our asymptotic estimates do not depend on
![]() $\varepsilon $
. Call a point
$\varepsilon $
. Call a point
![]() $(j,l) \in [n/2] \times \mathbb {Z}$
black
Footnote
8
if
$(j,l) \in [n/2] \times \mathbb {Z}$
black
Footnote
8
if
and white otherwise. We let
![]() $B = B_{n,\xi }, W = W_{n,\xi }$
denote the black and white points of
$B = B_{n,\xi }, W = W_{n,\xi }$
denote the black and white points of
![]() $[n/2] \times \mathbb {Z}$
respectively; thus we have the partition
$[n/2] \times \mathbb {Z}$
respectively; thus we have the partition
![]() $[n/2] \times \mathbb {Z} = B \uplus W$
.
$[n/2] \times \mathbb {Z} = B \uplus W$
.
Lemma 7.2 (Cancellation for white points)
If
![]() $(j,l)$
is white, then
$(j,l)$
is white, then
Proof. If
![]() $\mathbf {a}_1,\mathbf {a}_2$
are independent copies of
$\mathbf {a}_1,\mathbf {a}_2$
are independent copies of
![]() $\mathbf {Geom}(2)$
, then after conditioning to the event
$\mathbf {Geom}(2)$
, then after conditioning to the event
![]() $\mathbf {a}_1+\mathbf {a}_2 = 3$
, the pair
$\mathbf {a}_1+\mathbf {a}_2 = 3$
, the pair
![]() $(\mathbf {a}_1,\mathbf {a}_2)$
is equal to either
$(\mathbf {a}_1,\mathbf {a}_2)$
is equal to either
![]() $(1,2)$
or
$(1,2)$
or
![]() $(2,1)$
, with each pair occurring with (conditional) probability
$(2,1)$
, with each pair occurring with (conditional) probability
![]() $1/2$
. From equation (7.4), we thus have
$1/2$
. From equation (7.4), we thus have
for any x, so that
We specialise to the case
![]() $x := 3^{2j-2} 2^{-l}$
. By equation (7.7), we have
$x := 3^{2j-2} 2^{-l}$
. By equation (7.7), we have
and hence by elementary trigonometry
By hypothesis we have
and the claim now follows by Taylor expansion (if
![]() $\varepsilon $
is small enough); indeed one can even obtain an upper bound of
$\varepsilon $
is small enough); indeed one can even obtain an upper bound of
![]() $\exp (-c\varepsilon ^2)$
for some absolute constant
$\exp (-c\varepsilon ^2)$
for some absolute constant
![]() $c>0$
independent of
$c>0$
independent of
![]() $\varepsilon $
.
$\varepsilon $
.
From the above lemma, equation (7.6) and the law of total probability, we see that
As we shall see later, we can interpret the
![]() $(j,\mathbf {b}_{[1,j]})$
with
$(j,\mathbf {b}_{[1,j]})$
with
![]() $\mathbf {b}_j=3$
as a two-dimensional renewal process. To establish Proposition 7.1 (and thus Proposition 1.17 and Theorem 1.3), it thus suffices to show the following estimate.
$\mathbf {b}_j=3$
as a two-dimensional renewal process. To establish Proposition 7.1 (and thus Proposition 1.17 and Theorem 1.3), it thus suffices to show the following estimate.
Proposition 7.3 (Renewal process encounters many white points)
We remark that this proposition is of a simpler nature to establish than Proposition 7.1 as it is entirely ‘non-negative’; it does not require the need to capture any cancellation in an oscillating sum, as was the case in Proposition 7.1.
7.2 Deterministic structural analysis of black points
The proof of Proposition 7.3 consists of a ‘deterministic’ part, in which we understand the structure of the white set W (or the black set B), and a ‘probabilistic’ part, in which we control the random walk
![]() $\mathbf {b}_{[1,j]}$
and the events
$\mathbf {b}_{[1,j]}$
and the events
![]() $\mathbf {b}_j=3$
. We begin with the former task. Define a triangle to be a subset
$\mathbf {b}_j=3$
. We begin with the former task. Define a triangle to be a subset
![]() $\Delta $
of
$\Delta $
of
![]() $(\mathbb {N}+1) \times \mathbb {Z}$
of the form
$(\mathbb {N}+1) \times \mathbb {Z}$
of the form
for some
![]() $(j_\Delta , l_\Delta ) \in (\mathbb {N}+1) \times \mathbb {Z}$
(which we call the top-left corner of
$(j_\Delta , l_\Delta ) \in (\mathbb {N}+1) \times \mathbb {Z}$
(which we call the top-left corner of
![]() $\Delta $
) and some
$\Delta $
) and some
![]() $s_\Delta \geq 0$
(which we call the size of
$s_\Delta \geq 0$
(which we call the size of
![]() $\Delta $
); see Figure 2.
$\Delta $
); see Figure 2.

Figure 2 A triangle
![]() $\Delta $
, which we have drawn as a solid region rather than as a subset of the discrete lattice
$\Delta $
, which we have drawn as a solid region rather than as a subset of the discrete lattice
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Lemma 7.4 (Structure of black set)
The black set
![]() $B \subset [n/2] \times \mathbb {Z}$
of points
$B \subset [n/2] \times \mathbb {Z}$
of points
![]() $(j,l)$
with
$(j,l)$
with
![]() $|\theta (j,l)| \leq \varepsilon $
can be expressed as a disjoint union
$|\theta (j,l)| \leq \varepsilon $
can be expressed as a disjoint union
of triangles
![]() $\Delta $
, each of which is contained in
$\Delta $
, each of which is contained in
![]() $[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
. Furthermore, any two triangles
$[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
. Furthermore, any two triangles
![]() $\Delta ,\Delta '$
in
$\Delta ,\Delta '$
in
![]() ${\mathcal T}$
are separated by a distance
${\mathcal T}$
are separated by a distance
![]() $\geq \frac {1}{10} \log \frac {1}{\varepsilon }$
(using the Euclidean metric on
$\geq \frac {1}{10} \log \frac {1}{\varepsilon }$
(using the Euclidean metric on
![]() $[n/2] \times \mathbb {Z} \subset \mathbb {R}^2$
). (See Figure 3.)
$[n/2] \times \mathbb {Z} \subset \mathbb {R}^2$
). (See Figure 3.)

Figure 3 The black set is a union of triangles, in the strip
![]() $[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
, that are separated from each other by
$[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
, that are separated from each other by
![]() $\gg \log \frac {1}{\varepsilon }$
. The red dots depict (a portion of) a renewal process
$\gg \log \frac {1}{\varepsilon }$
. The red dots depict (a portion of) a renewal process
![]() $\mathbf {v}_1, \mathbf {v}_{[1,2]}, \mathbf {v}_{[1,3]}$
that we will encounter later in this section; our main objective will be to establish that this process usually contains a fair number of white points. We remark that the average slope
$\mathbf {v}_1, \mathbf {v}_{[1,2]}, \mathbf {v}_{[1,3]}$
that we will encounter later in this section; our main objective will be to establish that this process usually contains a fair number of white points. We remark that the average slope
![]() $\frac {16}{4}=4$
of this renewal process will exceed the slope
$\frac {16}{4}=4$
of this renewal process will exceed the slope
![]() $\frac {\log 9}{\log 2} \approx 3.17$
of the triangle diagonals, so that the process tends to exit a given triangle through its horizontal side. The coordinate j increases in the rightward direction, while the coordinate l increases in the upward direction.
$\frac {\log 9}{\log 2} \approx 3.17$
of the triangle diagonals, so that the process tends to exit a given triangle through its horizontal side. The coordinate j increases in the rightward direction, while the coordinate l increases in the upward direction.
Proof. We first observe some simple relations between adjacent values of
![]() $\theta $
. From equation (7.8) (or equation (7.7)), we observe the identity
$\theta $
. From equation (7.8) (or equation (7.7)), we observe the identity
whenever
![]() $j \leq j_*$
and
$j \leq j_*$
and
![]() $l \geq l_*$
. Thus, for instance,
$l \geq l_*$
. Thus, for instance,
and
Among other things, this implies that
and hence by the triangle inequality
These identities have the following consequences. Call a point
![]() $(j,l) \in [n/2] \times \mathbb {Z}$
weakly black if
$(j,l) \in [n/2] \times \mathbb {Z}$
weakly black if
Clearly any black point is weakly black. We have the following further claims.
-
(i) If
 $(j,l)$
is weakly black, and either
$(j,l)$
is weakly black, and either
 $(j+1,l)$
or
$(j+1,l)$
or
 $(j,l-1)$
is black, then
$(j,l-1)$
is black, then
 $(j,l)$
is black. (This follows from equation (7.13) or (7.14) respectively.)
$(j,l)$
is black. (This follows from equation (7.13) or (7.14) respectively.) -
(ii) If
 $(j+1,l), (j,l-1)$
are weakly black, then
$(j+1,l), (j,l-1)$
are weakly black, then
 $(j,l)$
is also weakly black. (Indeed, from equation (7.15), we have
$(j,l)$
is also weakly black. (Indeed, from equation (7.15), we have
 $|\theta (j,l)| \leq \frac {5}{100}$
, and the claim now follows from equation (7.13) or (7.14).)
$|\theta (j,l)| \leq \frac {5}{100}$
, and the claim now follows from equation (7.13) or (7.14).) -
(iii) If
 $(j-1, l)$
and
$(j-1, l)$
and
 $(j,l-1)$
are weakly black, then
$(j,l-1)$
are weakly black, then
 $(j,l)$
is also weakly black. (Indeed, from equation (7.13), we have
$(j,l)$
is also weakly black. (Indeed, from equation (7.13), we have
 $|\theta (j,l)| \leq \frac {9}{100}$
, and the claim now follows from equation (7.14).)
$|\theta (j,l)| \leq \frac {9}{100}$
, and the claim now follows from equation (7.14).)
Now we begin the proof of the lemma. Suppose
![]() $(j,l) \in [n/2] \times \mathbb {Z}$
is black, then by equations (7.9) and (7.8), we have
$(j,l) \in [n/2] \times \mathbb {Z}$
is black, then by equations (7.9) and (7.8), we have
and hence
On the other hand, since
![]() $\xi $
is not a multiple of
$\xi $
is not a multiple of
![]() $3$
, the expression
$3$
, the expression
![]() $\frac {\xi 3^{n-1} (2^{-l+1} \bmod 3^n)}{3^n}$
is either equal to
$\frac {\xi 3^{n-1} (2^{-l+1} \bmod 3^n)}{3^n}$
is either equal to
![]() $1/3$
or
$1/3$
or
![]() $2/3$
mod
$2/3$
mod
![]() $\mathbb {Z}$
. We conclude that
$\mathbb {Z}$
. We conclude that
so the black points in
![]() $[n/2] \times \mathbb {Z}$
actually lie in
$[n/2] \times \mathbb {Z}$
actually lie in
![]() $[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
.
$[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
.
Suppose that
![]() $(j,l) \in [n/2] \times \mathbb {Z}$
is such that
$(j,l) \in [n/2] \times \mathbb {Z}$
is such that
![]() $(j,l')$
is black for all
$(j,l')$
is black for all
![]() $l' \geq l$
; thus
$l' \geq l$
; thus
for all
![]() $l' \geq l$
. From equation (7.14), this implies that
$l' \geq l$
. From equation (7.14), this implies that
for all
![]() $l' \geq l$
, hence
$l' \geq l$
, hence
for all
![]() $l' \geq l$
. Repeating the proof of equation (7.16), one concludes that
$l' \geq l$
. Repeating the proof of equation (7.16), one concludes that
which is absurd for
![]() $l'$
large enough. Thus it is not possible for
$l'$
large enough. Thus it is not possible for
![]() $(j,l')$
to be black for all
$(j,l')$
to be black for all
![]() $l' \geq l$
.
$l' \geq l$
.

Figure 4 The proof of Lemma 7.4. The points connecting
![]() $(j,l)$
to
$(j,l)$
to
![]() $(j,l_*)$
, and from
$(j,l_*)$
, and from
![]() $(j,l_*)$
to
$(j,l_*)$
to
![]() $(j_*,l_*)$
, are known to be black, while the points
$(j_*,l_*)$
, are known to be black, while the points
![]() $(j, l_*+1), (j_*-1, l_*)$
are known to be white. The point
$(j, l_*+1), (j_*-1, l_*)$
are known to be white. The point
![]() $(j',l')$
can be in various locations, as illustrated by the red dots here. From equation (7.18), one can obtain that every point in the dashed triangle
$(j',l')$
can be in various locations, as illustrated by the red dots here. From equation (7.18), one can obtain that every point in the dashed triangle
![]() $\Delta _*$
is black (and every point in the Case 1 region is weakly black), which can treat the Case 1 locations of
$\Delta _*$
is black (and every point in the Case 1 region is weakly black), which can treat the Case 1 locations of
![]() $(j',l')$
(and also forces
$(j',l')$
(and also forces
![]() $(j,l)$
to lie inside
$(j,l)$
to lie inside
![]() $\Delta _*$
). In Case 2,
$\Delta _*$
). In Case 2,
![]() $(j',l')$
can be to the right or left of
$(j',l')$
can be to the right or left of
![]() $(j,l_*+1)$
, but in either case one can show that if
$(j,l_*+1)$
, but in either case one can show that if
![]() $(j',l')$
is black, then
$(j',l')$
is black, then
![]() $(j',l_*+1)$
(displayed here in blue) is weakly black and hence
$(j',l_*+1)$
(displayed here in blue) is weakly black and hence
![]() $(j,l_*+1)$
is weakly black and in fact black, a contradiction. Similarly, in Case 3,
$(j,l_*+1)$
is weakly black and in fact black, a contradiction. Similarly, in Case 3,
![]() $(j',l')$
can be above or below
$(j',l')$
can be above or below
![]() $(j_*-1,l_*)$
, but in either case one can show that if
$(j_*-1,l_*)$
, but in either case one can show that if
![]() $(j',l')$
is black, then so
$(j',l')$
is black, then so
![]() $(j_*-1,l')$
(displayed here in green) is weakly black and hence
$(j_*-1,l')$
(displayed here in green) is weakly black and hence
![]() $(j_*-1,l_*)$
is weakly black and in fact black, again giving a contradiction.
$(j_*-1,l_*)$
is weakly black and in fact black, again giving a contradiction.
Now let
![]() $(j,l) \in [n/2] \times \mathbb {Z}$
be black. By the preceding discussion, there exists a unique
$(j,l) \in [n/2] \times \mathbb {Z}$
be black. By the preceding discussion, there exists a unique
![]() $l_* = l_*(j,l) \geq l$
such that
$l_* = l_*(j,l) \geq l$
such that
![]() $(j,l')$
is black for all
$(j,l')$
is black for all
![]() $l \leq l' \leq l_*$
, but such that
$l \leq l' \leq l_*$
, but such that
![]() $(j,l_*+1)$
is white. Now let
$(j,l_*+1)$
is white. Now let
![]() $j_* = j_*(j,l) \leq j$
be the unique positive integer such that
$j_* = j_*(j,l) \leq j$
be the unique positive integer such that
![]() $(j',l_*)$
is black for all
$(j',l_*)$
is black for all
![]() $j_* \leq j' \leq j$
, but such that either
$j_* \leq j' \leq j$
, but such that either
![]() $j_*=1$
or
$j_*=1$
or
![]() $(j_*-1,l_*)$
is white. Informally,
$(j_*-1,l_*)$
is white. Informally,
![]() $(j_*,l_*)$
is obtained from
$(j_*,l_*)$
is obtained from
![]() $(j,l)$
by first moving upward as far as one can go in B, then moving leftwards as far as one can go in B; see Figure 4. As one should expect from glancing at this figure (or Figure 3),
$(j,l)$
by first moving upward as far as one can go in B, then moving leftwards as far as one can go in B; see Figure 4. As one should expect from glancing at this figure (or Figure 3),
![]() $(j_*,l_*)$
should be the top-left corner of the triangle containing
$(j_*,l_*)$
should be the top-left corner of the triangle containing
![]() $(j,l)$
, and the arguments below are intended to support this claim.
$(j,l)$
, and the arguments below are intended to support this claim.
By construction,
![]() $(j_*,l_*)$
is black; thus by equation (7.9), we have
$(j_*,l_*)$
is black; thus by equation (7.9), we have
for some
![]() $s_* \geq 0$
. From equation (7.12) this implies in particular that
$s_* \geq 0$
. From equation (7.12) this implies in particular that
whenever
![]() $j' \geq j_*, l' \geq l_*$
, with equality whenever the right-hand side is strictly less than
$j' \geq j_*, l' \geq l_*$
, with equality whenever the right-hand side is strictly less than
![]() $1/2$
.
$1/2$
.
Let
![]() $\Delta _*$
denote the triangle with top-left corner
$\Delta _*$
denote the triangle with top-left corner
![]() $(j_*,l_*)$
and size
$(j_*,l_*)$
and size
![]() $s_*$
. If
$s_*$
. If
![]() $(j',l') \in \Delta _*$
, then by equation (7.18), we have
$(j',l') \in \Delta _*$
, then by equation (7.18), we have
and hence every element of
![]() $\Delta _*$
is black (and thus lies in
$\Delta _*$
is black (and thus lies in
![]() $[\frac {n}{2} - c \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
).
$[\frac {n}{2} - c \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
).
Next, we make the following claim:
-
(*) Every point
 $(j',l') \in [n/2] \times \mathbb {Z}$
that lies outside of
$(j',l') \in [n/2] \times \mathbb {Z}$
that lies outside of
 $\Delta _*$
, but is at a distance of at most
$\Delta _*$
, but is at a distance of at most
 $\frac {1}{10} \log \frac {1}{\varepsilon }$
to
$\frac {1}{10} \log \frac {1}{\varepsilon }$
to
 $\Delta _*$
, is white.
$\Delta _*$
, is white.
To verify Claim (*), we divide into three cases (see Figure 4):
Case 1:
![]() $j' \geq j_*, l' \leq l_*$
. In this case we have from equation (7.11) that
$j' \geq j_*, l' \leq l_*$
. In this case we have from equation (7.11) that
and hence
Applying the equality case of equation (7.18), we conclude that
and thus
![]() $(j',l')$
is white as claimed.
$(j',l')$
is white as claimed.
Case 2:
![]() $j' \geq j_*, l'> l_*$
. In this case we have from equation (7.11) that
$j' \geq j_*, l'> l_*$
. In this case we have from equation (7.11) that
and
(say). Suppose for contradiction that
![]() $(j',l')$
was black; thus
$(j',l')$
was black; thus
From equations (7.19) and (7.12) (or equation (7.14)) this implies that
so in particular
![]() $(j',l_*+1)$
is weakly black.
$(j',l_*+1)$
is weakly black.
If
![]() $j' \geq j$
, then from equations (7.18) and (7.20), we also have
$j' \geq j$
, then from equations (7.18) and (7.20), we also have
thus
![]() $(j'-1,l_*)$
is weakly black. Applying claim (ii) and the fact that
$(j'-1,l_*)$
is weakly black. Applying claim (ii) and the fact that
![]() $(j',l_*+1)$
is weakly black, we conclude that
$(j',l_*+1)$
is weakly black, we conclude that
![]() $(j'-1,l_*+1)$
is weakly black. Iterating this argument, we conclude that
$(j'-1,l_*+1)$
is weakly black. Iterating this argument, we conclude that
![]() $(j'',l_*+1)$
is weakly black for all
$(j'',l_*+1)$
is weakly black for all
![]() $j_* \leq j'' \leq j'$
. In particular,
$j_* \leq j'' \leq j'$
. In particular,
![]() $(j,l_*+1)$
is weakly black; since
$(j,l_*+1)$
is weakly black; since
![]() $(j,l_*)$
is black by construction of
$(j,l_*)$
is black by construction of
![]() $l_*$
, we conclude from Claim (i) that
$l_*$
, we conclude from Claim (i) that
![]() $(j,l_*+1)$
is black. But this contradicts the construction of
$(j,l_*+1)$
is black. But this contradicts the construction of
![]() $l_*$
.
$l_*$
.
Now suppose that
![]() $j' < j$
. From construction of
$j' < j$
. From construction of
![]() $l_*, j_*$
, we see that
$l_*, j_*$
, we see that
![]() $(j'+1,l_*)$
is black, hence weakly black; since
$(j'+1,l_*)$
is black, hence weakly black; since
![]() $(j',l_*+1)$
is weakly black, we conclude from Claim (iii) that
$(j',l_*+1)$
is weakly black, we conclude from Claim (iii) that
![]() $(j'+1,l_*+1)$
is weakly black. Iterating this argument, we conclude that
$(j'+1,l_*+1)$
is weakly black. Iterating this argument, we conclude that
![]() $(j'',l_*+1)$
is weakly black for all
$(j'',l_*+1)$
is weakly black for all
![]() $j' \leq j'' \leq j$
; thus in particular
$j' \leq j'' \leq j$
; thus in particular
![]() $(j,l_*+1)$
is weakly black, and we obtain a contradiction as before.
$(j,l_*+1)$
is weakly black, and we obtain a contradiction as before.
Case 3:
![]() $j' < j_*$
. Clearly this implies
$j' < j_*$
. Clearly this implies
![]() $j_*> 1$
; also, from equation (7.11), we have
$j_*> 1$
; also, from equation (7.11), we have
and
Suppose for contradiction that
![]() $(j',l')$
was black; thus
$(j',l')$
was black; thus
From equations (7.23) and (7.12) (or equation (7.13)) we thus have
If
![]() $l' \geq l_*$
, then from equations (7.22) and (7.12), we then have
$l' \geq l_*$
, then from equations (7.22) and (7.12), we then have
so
![]() $(j_*-1,l_*)$
is weakly black. By construction of
$(j_*-1,l_*)$
is weakly black. By construction of
![]() $j_*$
,
$j_*$
,
![]() $(j_*,l_*)$
is black, hence by Claim (i)
$(j_*,l_*)$
is black, hence by Claim (i)
![]() $(j_*-1,l_*)$
is black, contradicting the construction of
$(j_*-1,l_*)$
is black, contradicting the construction of
![]() $j_*$
.
$j_*$
.
Now suppose that
![]() $l' < l_*$
. From equation (7.24),
$l' < l_*$
. From equation (7.24),
![]() $(j_*-1, l')$
is weakly black. On the other hand, from equations (7.22) and (7.18) that
$(j_*-1, l')$
is weakly black. On the other hand, from equations (7.22) and (7.18) that
so
![]() $(j_*, l'+1)$
is also weakly black. By Claim (ii), this implies that
$(j_*, l'+1)$
is also weakly black. By Claim (ii), this implies that
![]() $(j_*-1, l'+1)$
is weakly black. Iterating this argument, we see that
$(j_*-1, l'+1)$
is weakly black. Iterating this argument, we see that
![]() $(j_*-1, l'')$
is weakly black for all
$(j_*-1, l'')$
is weakly black for all
![]() $l' \leq l'' \leq l_*$
, hence
$l' \leq l'' \leq l_*$
, hence
![]() $(j_*-1,l_*)$
is weakly black and we can obtain a contradiction as before. This concludes the treatment of Case 3 of Claim (*).
$(j_*-1,l_*)$
is weakly black and we can obtain a contradiction as before. This concludes the treatment of Case 3 of Claim (*).
We have now verified Claim (*) in all cases. From this claim and the construction
![]() $(j_*,l_*)$
from
$(j_*,l_*)$
from
![]() $(j,l)$
, we now see that
$(j,l)$
, we now see that
![]() $(j,l)$
must lie in
$(j,l)$
must lie in
![]() $\Delta _*$
; indeed, if
$\Delta _*$
; indeed, if
![]() $(j,l_*)$
was outside of
$(j,l_*)$
was outside of
![]() $\Delta _*$
, then one of the (necessarily black) points between
$\Delta _*$
, then one of the (necessarily black) points between
![]() $(j_*,l_*)$
and
$(j_*,l_*)$
and
![]() $(j,l_*)$
would violate Case 1 of Claim (*), and similarly if
$(j,l_*)$
would violate Case 1 of Claim (*), and similarly if
![]() $(j,l_*)$
was in
$(j,l_*)$
was in
![]() $\Delta _*$
but
$\Delta _*$
but
![]() $(j,l)$
was outside
$(j,l)$
was outside
![]() $\Delta _*$
, then one of the (necessarily black points) between
$\Delta _*$
, then one of the (necessarily black points) between
![]() $(j,l_*)$
and
$(j,l_*)$
and
![]() $(j,l)$
would again violate Case 1 of Claim (*); see Figure 4. Furthermore, for any
$(j,l)$
would again violate Case 1 of Claim (*); see Figure 4. Furthermore, for any
![]() $(j',l') \in \Delta _*$
, that
$(j',l') \in \Delta _*$
, that
![]() $l_*(j',l') = l_*$
and
$l_*(j',l') = l_*$
and
![]() $j_*(j',l') = j_*$
. In other words, we have
$j_*(j',l') = j_*$
. In other words, we have
and so the triangles
![]() $\Delta _*$
form a partition of B. By the preceding arguments, we see that these triangles lie in
$\Delta _*$
form a partition of B. By the preceding arguments, we see that these triangles lie in
![]() $[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
and are separated from each other by at least
$[\frac {n}{2} - \frac {1}{10} \log \frac {1}{\varepsilon }] \times \mathbb {Z}$
and are separated from each other by at least
![]() $\frac {1}{10} \log \frac {1}{\varepsilon }$
. This proves the lemma.
$\frac {1}{10} \log \frac {1}{\varepsilon }$
. This proves the lemma.
Remark 7.5. One can say a little bit more about the structure of the black set B; for instance, from Euler’s theorem, we see that B is periodic with respect to the vertical shift
![]() $(0, 2 \times 3^{n-1})$
(cf. Lemma 1.12), and one could use Baker’s theorem [Reference Baker2] that (among other things) establishes a Diophantine property of
$(0, 2 \times 3^{n-1})$
(cf. Lemma 1.12), and one could use Baker’s theorem [Reference Baker2] that (among other things) establishes a Diophantine property of
![]() $\frac {\log 3}{\log 2}$
in order to obtain some further control on B. However, we will not exploit any further structure of the black set in our arguments beyond what is provided by Lemma 7.4.
$\frac {\log 3}{\log 2}$
in order to obtain some further control on B. However, we will not exploit any further structure of the black set in our arguments beyond what is provided by Lemma 7.4.
7.3 Formulation in terms of holding time
We now return to the probabilistic portion of the proof of Proposition 7.3. Currently we have a finite sequence
![]() $\mathbf {b}_1,\dots ,\mathbf {b}_{\lfloor n/2\rfloor }$
of random variables that are iid copies of the sum
$\mathbf {b}_1,\dots ,\mathbf {b}_{\lfloor n/2\rfloor }$
of random variables that are iid copies of the sum
![]() $\mathbf {a}_1+\mathbf {a}_2$
of two independent copies
$\mathbf {a}_1+\mathbf {a}_2$
of two independent copies
![]() $\mathbf {a}_1,\mathbf {a}_2$
of
$\mathbf {a}_1,\mathbf {a}_2$
of
![]() $\mathbf {Geom}(2)$
. We may extend this sequence to an infinite sequence
$\mathbf {Geom}(2)$
. We may extend this sequence to an infinite sequence
![]() $\mathbf {b}_1,\mathbf {b}_2,\mathbf {b}_3,\dots $
of iid copies of
$\mathbf {b}_1,\mathbf {b}_2,\mathbf {b}_3,\dots $
of iid copies of
![]() $\mathbf {a}_1+\mathbf {a}_2$
. Recalling from definition that W is a subset of
$\mathbf {a}_1+\mathbf {a}_2$
. Recalling from definition that W is a subset of
![]() $[n/2] \times \mathbb {Z}$
, the point
$[n/2] \times \mathbb {Z}$
, the point
![]() $(j,\mathbf {b}_{[1,j]})$
can only lie in W when
$(j,\mathbf {b}_{[1,j]})$
can only lie in W when
![]() $j \in [n/2]$
. Thus the left-hand side of equation (7.10) can then be written as
$j \in [n/2]$
. Thus the left-hand side of equation (7.10) can then be written as
We now describe the random set
![]() $\{ (j,\mathbf {b}_{[1,j]}): j \in \mathbb {N}+1, \mathbf {b}_j = 3\}$
asFootnote
9
a two-dimensional renewal process (a special case of a renewal-reward process). Since the events
$\{ (j,\mathbf {b}_{[1,j]}): j \in \mathbb {N}+1, \mathbf {b}_j = 3\}$
asFootnote
9
a two-dimensional renewal process (a special case of a renewal-reward process). Since the events
![]() $\mathbf {b}_j=3$
are independent and each occur with probability
$\mathbf {b}_j=3$
are independent and each occur with probability
we see that almost surely one has
![]() $\mathbf {b}_j=3$
for at least one
$\mathbf {b}_j=3$
for at least one
![]() $j \in \mathbb {N}$
. Define the two-dimensional holding time
$j \in \mathbb {N}$
. Define the two-dimensional holding time
![]() $\mathbf {Hold} \in (\mathbb {N}+1) \times (\mathbb {N}+2)$
to be the random shift
$\mathbf {Hold} \in (\mathbb {N}+1) \times (\mathbb {N}+2)$
to be the random shift
![]() $(\mathbf {j},\mathbf {b}_{[1,\mathbf {j}]})$
, where
$(\mathbf {j},\mathbf {b}_{[1,\mathbf {j}]})$
, where
![]() $\mathbf {j}$
is the least positive integer for which
$\mathbf {j}$
is the least positive integer for which
![]() $\mathbf {b}_{\mathbf {j}} =3$
; this random variable is almost surely well defined. Note from equation (7.25) that the first component
$\mathbf {b}_{\mathbf {j}} =3$
; this random variable is almost surely well defined. Note from equation (7.25) that the first component
![]() $\mathbf {j}$
of
$\mathbf {j}$
of
![]() $\mathbf {Hold}$
has the distribution
$\mathbf {Hold}$
has the distribution
![]() $\mathbf {j} \equiv \mathbf {Geom}(4)$
. A little thought then reveals that the random set
$\mathbf {j} \equiv \mathbf {Geom}(4)$
. A little thought then reveals that the random set
has the same distribution as the random set
where
![]() $\mathbf {v}_1, \mathbf {v}_2, \dots $
are iid copies of
$\mathbf {v}_1, \mathbf {v}_2, \dots $
are iid copies of
![]() $\mathbf {Hold}$
, and we extend the summation notation in equation (1.6) to the
$\mathbf {Hold}$
, and we extend the summation notation in equation (1.6) to the
![]() $\mathbf {v}_j$
; thus, for instance,
$\mathbf {v}_j$
; thus, for instance,
![]() $\mathbf {v}_{[1,k]} := \mathbf {v}_1 + \dots + \mathbf {v}_k$
. In particular, we have
$\mathbf {v}_{[1,k]} := \mathbf {v}_1 + \dots + \mathbf {v}_k$
. In particular, we have
and so we can write the left-hand side of equation (7.10) as
note that all but finitely many of the terms in this product are equal to
![]() $1$
.
$1$
.
We now pause our analysis of equations (7.10) and (7.28) to record some basic properties about the distribution of
![]() $\mathbf {Hold}$
.
$\mathbf {Hold}$
.
Lemma 7.6 (Basic properties of holding time)
The random variable
![]() $\mathbf {Hold}$
has exponential tail (in the sense of equation (2.3)), is not supported in any coset of any proper subgroup of
$\mathbf {Hold}$
has exponential tail (in the sense of equation (2.3)), is not supported in any coset of any proper subgroup of
![]() $\mathbb {Z}^2$
and has mean
$\mathbb {Z}^2$
and has mean
![]() $(4,16)$
. In particular, the conclusion of Lemma 2.2 holds for
$(4,16)$
. In particular, the conclusion of Lemma 2.2 holds for
![]() $\mathbf {Hold}$
with
$\mathbf {Hold}$
with
![]() $\vec \mu = (4,16)$
.
$\vec \mu = (4,16)$
.
Proof. From the definition of
![]() $\mathbf {Hold}$
and equation (7.25), we see that
$\mathbf {Hold}$
and equation (7.25), we see that
![]() $\mathbf {Hold}$
is equal to
$\mathbf {Hold}$
is equal to
![]() $(1,3)$
with probability
$(1,3)$
with probability
![]() $1/4$
, and on the remaining event of probability
$1/4$
, and on the remaining event of probability
![]() $3/4$
, it has the distribution of
$3/4$
, it has the distribution of
![]() $(1,\mathbf {Pascal}') + \mathbf {Hold}'$
, where
$(1,\mathbf {Pascal}') + \mathbf {Hold}'$
, where
![]() $\mathbf {Pascal}'$
is a copy of
$\mathbf {Pascal}'$
is a copy of
![]() $\mathbf {Pascal}$
that is conditioned to the event
$\mathbf {Pascal}$
that is conditioned to the event
![]() $\mathbf {Pascal} \neq 3$
, so that
$\mathbf {Pascal} \neq 3$
, so that
for
![]() $b \in \mathbb {N}+2 \backslash \{3\}$
, and
$b \in \mathbb {N}+2 \backslash \{3\}$
, and
![]() $\mathbf {Hold}'$
is a copy of
$\mathbf {Hold}'$
is a copy of
![]() $\mathbf {Hold}$
that is independent of
$\mathbf {Hold}$
that is independent of
![]() $\mathbf {Pascal}'$
. Thus
$\mathbf {Pascal}'$
. Thus
![]() $\mathbf {Hold}$
has the distribution of
$\mathbf {Hold}$
has the distribution of
![]() $(1,3) + (1,\mathbf {b}^{\prime }_1) + \dots + (1,\mathbf {b}^{\prime }_{\mathbf {j}-1})$
, where
$(1,3) + (1,\mathbf {b}^{\prime }_1) + \dots + (1,\mathbf {b}^{\prime }_{\mathbf {j}-1})$
, where
![]() $\mathbf {b}^{\prime }_1,\mathbf {b}^{\prime }_2,\dots $
are iid copies of
$\mathbf {b}^{\prime }_1,\mathbf {b}^{\prime }_2,\dots $
are iid copies of
![]() $\mathbf {Pascal}'$
and
$\mathbf {Pascal}'$
and
![]() $\mathbf {j} \equiv \mathbf {Geom}(4)$
is independent of the
$\mathbf {j} \equiv \mathbf {Geom}(4)$
is independent of the
![]() $\mathbf {b}^{\prime }_j$
. In particular, for any
$\mathbf {b}^{\prime }_j$
. In particular, for any
![]() $k = (k_1,k_2) \in \mathbb {R}^2$
, one has from monotone convergence that
$k = (k_1,k_2) \in \mathbb {R}^2$
, one has from monotone convergence that
 $$ \begin{align} \mathbb{E} \exp( \mathbf{Hold} \cdot k ) = \sum_{j \in \mathbb{N}} \frac{1}{4} \left(\frac{3}{4}\right)^{j-1} \exp\left( (1,3) \cdot k\right) \left(\mathbb{E} \exp( (1,\mathbf{Pascal}') \cdot k) \right)^j. \end{align} $$
$$ \begin{align} \mathbb{E} \exp( \mathbf{Hold} \cdot k ) = \sum_{j \in \mathbb{N}} \frac{1}{4} \left(\frac{3}{4}\right)^{j-1} \exp\left( (1,3) \cdot k\right) \left(\mathbb{E} \exp( (1,\mathbf{Pascal}') \cdot k) \right)^j. \end{align} $$
From equation (7.29) and dominated convergence, we have
![]() $\mathbb {E} \exp ( (1,\mathbf {Pascal}') \cdot k ) < \frac {4}{3}$
for k sufficiently close to
$\mathbb {E} \exp ( (1,\mathbf {Pascal}') \cdot k ) < \frac {4}{3}$
for k sufficiently close to
![]() $0$
, which by equation (7.30) implies that
$0$
, which by equation (7.30) implies that
![]() $\mathbb {E} \exp ( \mathbf {Hold} \cdot k ) < \infty $
for k sufficiently close to zero. This gives the exponential tail property by Markov’s inequality.
$\mathbb {E} \exp ( \mathbf {Hold} \cdot k ) < \infty $
for k sufficiently close to zero. This gives the exponential tail property by Markov’s inequality.
Since
![]() $\mathbf {Hold}$
attains the value
$\mathbf {Hold}$
attains the value
![]() $(1,3)+(1,b)$
for any
$(1,3)+(1,b)$
for any
![]() $b \in \mathbb {N}+2 \backslash \{3\}$
with positive probability, as well as attaining
$b \in \mathbb {N}+2 \backslash \{3\}$
with positive probability, as well as attaining
![]() $(1,3)$
with positive probability, we see that the support of
$(1,3)$
with positive probability, we see that the support of
![]() $\mathbf {Hold}$
is not supported in any coset of any proper subgroup of
$\mathbf {Hold}$
is not supported in any coset of any proper subgroup of
![]() $\mathbb {Z}^2$
. Finally, from the description of
$\mathbb {Z}^2$
. Finally, from the description of
![]() $\mathbf {Hold}$
at the start of this proof we have
$\mathbf {Hold}$
at the start of this proof we have
also, from the definition of
![]() $\mathbf {Pascal}'$
, we have
$\mathbf {Pascal}'$
, we have
We conclude that
since
![]() $\mathbb {E} \mathbf {Pascal} = 2 \mathbb {E} \mathbf {Geom}(2) =4$
, we thus have
$\mathbb {E} \mathbf {Pascal} = 2 \mathbb {E} \mathbf {Geom}(2) =4$
, we thus have
![]() $\mathbb {E} \mathbf {Hold} = (4,16)$
as required.
$\mathbb {E} \mathbf {Hold} = (4,16)$
as required.
The following lemma allows us to control the distribution of first passage locations of renewal processes with holding times
![]() $\equiv \mathbf {Hold}$
, which will be important for us as it lets us understand how such renewal processes exit a given triangle
$\equiv \mathbf {Hold}$
, which will be important for us as it lets us understand how such renewal processes exit a given triangle
![]() $\Delta $
:
$\Delta $
:
Lemma 7.7 (Distribution of first passage location)
Let
![]() $\mathbf {v}_1,\mathbf {v}_2,\dots $
be iid copies of
$\mathbf {v}_1,\mathbf {v}_2,\dots $
be iid copies of
![]() $\mathbf {Hold}$
, and write
$\mathbf {Hold}$
, and write
![]() $\mathbf {v}_k = (\mathbf {j}_k,\mathbf {l}_k)$
. Let
$\mathbf {v}_k = (\mathbf {j}_k,\mathbf {l}_k)$
. Let
![]() $s \in \mathbb {N}$
, and define the first passage time
$s \in \mathbb {N}$
, and define the first passage time
![]() $\mathbf {k}$
to be the least positive integer such that
$\mathbf {k}$
to be the least positive integer such that
![]() $\mathbf {l}_{[1,k]}> s$
. Then for any
$\mathbf {l}_{[1,k]}> s$
. Then for any
![]() $j,l \in \mathbb {N}$
with
$j,l \in \mathbb {N}$
with
![]() $l> s$
, one has
$l> s$
, one has
 $$ \begin{align*}\mathbb{P}( \mathbf{v}_{[1,\mathbf{k}]} = (j,l) ) \ll \frac{e^{-c(l-s)}}{(1+s)^{1/2}} G_{1+s}\left( c\left(j - \frac{s}{4}\right) \right),\end{align*} $$
$$ \begin{align*}\mathbb{P}( \mathbf{v}_{[1,\mathbf{k}]} = (j,l) ) \ll \frac{e^{-c(l-s)}}{(1+s)^{1/2}} G_{1+s}\left( c\left(j - \frac{s}{4}\right) \right),\end{align*} $$
where
![]() $G_{1+s}(x) = \exp (-\frac {|x|^2}{1+s}) + \exp (-|x|)$
was the function defined in equation (2.2).
$G_{1+s}(x) = \exp (-\frac {|x|^2}{1+s}) + \exp (-|x|)$
was the function defined in equation (2.2).
Informally, this lemma asserts that as a rough first approximation one has
Proof. Note that by construction of
![]() $\mathbf {k}$
one has
$\mathbf {k}$
one has
![]() $\mathbf {l}_{[1,\mathbf {k}]} - \mathbf {l}_{\mathbf {k}} \leq s$
, so that
$\mathbf {l}_{[1,\mathbf {k}]} - \mathbf {l}_{\mathbf {k}} \leq s$
, so that
![]() $\mathbf {l}_{\mathbf {k}} \geq \mathbf {l}_{[1,\mathbf {k}]}-s$
. From the union bound, we therefore have
$\mathbf {l}_{\mathbf {k}} \geq \mathbf {l}_{[1,\mathbf {k}]}-s$
. From the union bound, we therefore have
since
![]() $\mathbf {v}_k$
has the exponential tail and is independent of
$\mathbf {v}_k$
has the exponential tail and is independent of
![]() $\mathbf {v}_1,\dots ,\mathbf {v}_{k-1}$
, we thus have
$\mathbf {v}_1,\dots ,\mathbf {v}_{k-1}$
, we thus have
 $$ \begin{align*}\mathbb{P}( \mathbf{v}_{[1,\mathbf{k}]} = (j,l) ) \ll \sum_{k \in \mathbb{N}+1} \sum_{l_k \geq l-s} \sum_{j_k \in \mathbb{N}+1} e^{- c(j_k+l_k)} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j-j_k,l-l_k) ).\end{align*} $$
$$ \begin{align*}\mathbb{P}( \mathbf{v}_{[1,\mathbf{k}]} = (j,l) ) \ll \sum_{k \in \mathbb{N}+1} \sum_{l_k \geq l-s} \sum_{j_k \in \mathbb{N}+1} e^{- c(j_k+l_k)} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j-j_k,l-l_k) ).\end{align*} $$
Writing
![]() $l_k = l - s + l^{\prime }_k$
, we then have
$l_k = l - s + l^{\prime }_k$
, we then have
 $$ \begin{align*} \mathbb{P}( \mathbf{v}_{[1,\mathbf{k}]} = (j,l) ) &\ll e^{-c(l-s)} \sum_{k \in \mathbb{N}+1} \sum_{l^{\prime}_k \in \mathbb{N}} \sum_{j_k \in \mathbb{N}+1} \\ &\quad\quad\quad e^{-c(j_k+l^{\prime}_k)} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j-j_k,s-l^{\prime}_k) ). \end{align*} $$
$$ \begin{align*} \mathbb{P}( \mathbf{v}_{[1,\mathbf{k}]} = (j,l) ) &\ll e^{-c(l-s)} \sum_{k \in \mathbb{N}+1} \sum_{l^{\prime}_k \in \mathbb{N}} \sum_{j_k \in \mathbb{N}+1} \\ &\quad\quad\quad e^{-c(j_k+l^{\prime}_k)} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j-j_k,s-l^{\prime}_k) ). \end{align*} $$
We can restrict to the region
![]() $l^{\prime }_k \leq s$
, since the summand vanishes otherwise. It now suffices to show that
$l^{\prime }_k \leq s$
, since the summand vanishes otherwise. It now suffices to show that
 $$ \begin{align} &\sum_{k \in \mathbb{N}+1} \sum_{0 \leq l_k' \leq s} \sum_{j_k \in \mathbb{N}+1} e^{- c(j_k+l^{\prime}_k)} \mathbb{P}\left( \mathbf{v}_{[1,k-1]} = (j-j_k,s-l^{\prime}_k) \right)\nonumber\\ &\quad \ll (1+s)^{-1/2} G_{1+s}\left( c \left(j - \frac{s}{4}\right) \right). \end{align} $$
$$ \begin{align} &\sum_{k \in \mathbb{N}+1} \sum_{0 \leq l_k' \leq s} \sum_{j_k \in \mathbb{N}+1} e^{- c(j_k+l^{\prime}_k)} \mathbb{P}\left( \mathbf{v}_{[1,k-1]} = (j-j_k,s-l^{\prime}_k) \right)\nonumber\\ &\quad \ll (1+s)^{-1/2} G_{1+s}\left( c \left(j - \frac{s}{4}\right) \right). \end{align} $$
This is in turn implied by
 $$ \begin{align} &\sum_{k \in \mathbb{N}+1} \sum_{0 \leq l_k' \leq s} e^{-cl^{\prime}_k} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j',s-l^{\prime}_k) ) \nonumber\\ &\quad \ll (1+s)^{-1/2} G_{1+s}\left( c\left(j' - \frac{s}{4}\right) \right) \end{align} $$
$$ \begin{align} &\sum_{k \in \mathbb{N}+1} \sum_{0 \leq l_k' \leq s} e^{-cl^{\prime}_k} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j',s-l^{\prime}_k) ) \nonumber\\ &\quad \ll (1+s)^{-1/2} G_{1+s}\left( c\left(j' - \frac{s}{4}\right) \right) \end{align} $$
for all
![]() $j' \in \mathbb {Z}$
, since equation (7.32) then follows by replacing
$j' \in \mathbb {Z}$
, since equation (7.32) then follows by replacing
![]() $j'$
by
$j'$
by
![]() $j - j_k$
, multiplying by
$j - j_k$
, multiplying by
![]() $\exp (-cj_k)$
, and summing in
$\exp (-cj_k)$
, and summing in
![]() $j_k$
(and adjusting the constants c appropriately). In a similar vein, it suffices to show that
$j_k$
(and adjusting the constants c appropriately). In a similar vein, it suffices to show that
 $$ \begin{align*}\sum_{k \in \mathbb{N}+1} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j',s') ) \ll (1+s')^{-1/2} G_{1+s'}\left( c \left(j' - \frac{s'}{4} \right) \right)\end{align*} $$
$$ \begin{align*}\sum_{k \in \mathbb{N}+1} \mathbb{P}( \mathbf{v}_{[1,k-1]} = (j',s') ) \ll (1+s')^{-1/2} G_{1+s'}\left( c \left(j' - \frac{s'}{4} \right) \right)\end{align*} $$
for all
![]() $s' \in \mathbb {N}$
, since equation (7.33) follows after setting
$s' \in \mathbb {N}$
, since equation (7.33) follows after setting
![]() $s' = s - l^{\prime }_k$
, multiplying by
$s' = s - l^{\prime }_k$
, multiplying by
![]() $\exp (-cl^{\prime }_k)$
, and summing in
$\exp (-cl^{\prime }_k)$
, and summing in
![]() $l^{\prime }_k$
(splitting into the regions
$l^{\prime }_k$
(splitting into the regions
![]() $l^{\prime }_k \leq s/2$
and
$l^{\prime }_k \leq s/2$
and
![]() $l^{\prime }_k> s/2$
if desired to simplify the calculations).
$l^{\prime }_k> s/2$
if desired to simplify the calculations).
From Lemma 7.6 and Lemma 2.2, one has
and the claim now follows from summing in k and a routine calculation (splitting for instance into the regions
![]() $16 (k-1) \in [s'/2,2s']$
,
$16 (k-1) \in [s'/2,2s']$
,
![]() $16(k-1) < s'/2$
, and
$16(k-1) < s'/2$
, and
![]() $16(k-1)>2s'$
).
$16(k-1)>2s'$
).
7.4 Recursively controlling a maximal expression
We return to the study of the left-hand side of equation (7.10), which we have expressed as equation (7.28). For any
![]() $(j,l) \in \mathbb {N}+1 \times \mathbb {Z}$
, let
$(j,l) \in \mathbb {N}+1 \times \mathbb {Z}$
, let
![]() $Q(j,l)$
denote the quantity
$Q(j,l)$
denote the quantity
then we have the recursive formula
Observe that for each
![]() $(j,l) \in \mathbb {N}+1 \times \mathbb {Z}$
, we have the conditional expectation
$(j,l) \in \mathbb {N}+1 \times \mathbb {Z}$
, we have the conditional expectation
 $$ \begin{align*}\mathbb{E}\left( \prod_{k \in \mathbb{N}+1} \exp( - \varepsilon^3 1_W(\mathbf{v}_{[1,k]}) ) | \mathbf{v}_1 = (j,l) \right) = Q(j,l)\end{align*} $$
$$ \begin{align*}\mathbb{E}\left( \prod_{k \in \mathbb{N}+1} \exp( - \varepsilon^3 1_W(\mathbf{v}_{[1,k]}) ) | \mathbf{v}_1 = (j,l) \right) = Q(j,l)\end{align*} $$
since after conditioning on
![]() $\mathbf {v}_1 = (j,l)$
, then the
$\mathbf {v}_1 = (j,l)$
, then the
![]() $\mathbf {v}_{[1,k]}$
have the same distribution as
$\mathbf {v}_{[1,k]}$
have the same distribution as
![]() $(j,l) + \mathbf {v}^{\prime }_{[1,k-1]}$
, where
$(j,l) + \mathbf {v}^{\prime }_{[1,k-1]}$
, where
![]() $\mathbf {v}^{\prime }_1,\mathbf {v}^{\prime }_2,\dots $
is another sequence of iid copies of
$\mathbf {v}^{\prime }_1,\mathbf {v}^{\prime }_2,\dots $
is another sequence of iid copies of
![]() $\mathbf {Hold}$
. Since
$\mathbf {Hold}$
. Since
![]() $\mathbf {v}_1$
has the distribution of
$\mathbf {v}_1$
has the distribution of
![]() $\mathbf {Hold}$
, we conclude from the law of total probability that
$\mathbf {Hold}$
, we conclude from the law of total probability that
From equation (7.28), we thus see that we can rewrite the desired estimate in equation (7.10) as
One can think of
![]() $Q(j,l)$
as a quantity controlling how often one encounters white points when one walks along a two-dimensional renewal process
$Q(j,l)$
as a quantity controlling how often one encounters white points when one walks along a two-dimensional renewal process
![]() $(j,l), (j,l) + \mathbf {v}_1, (j,l)+\mathbf {v}_{[1,2]}, \dots $
starting at
$(j,l), (j,l) + \mathbf {v}_1, (j,l)+\mathbf {v}_{[1,2]}, \dots $
starting at
![]() $(j,l)$
with holding times given by iid copies of
$(j,l)$
with holding times given by iid copies of
![]() $\mathbf {Hold}$
. The smaller this quantity is, the more white points one is likely to encounter. The main difficulty is thus to ensure that this renewal process is usually not trapped within the black triangles
$\mathbf {Hold}$
. The smaller this quantity is, the more white points one is likely to encounter. The main difficulty is thus to ensure that this renewal process is usually not trapped within the black triangles
![]() $\Delta $
from Lemma 7.4; as it turns out (and as may be evident from an inspection of Figure 3), the large triangles will be the most troublesome to handle (as they are so large compared to the narrow band of white points surrounding them that are provided by Lemma 7.4).
$\Delta $
from Lemma 7.4; as it turns out (and as may be evident from an inspection of Figure 3), the large triangles will be the most troublesome to handle (as they are so large compared to the narrow band of white points surrounding them that are provided by Lemma 7.4).
Suppose that we can prove a bound of the form
for all
![]() $(j,l) \in (\mathbb {N}+1) \times \mathbb {Z}$
; this is trivial for
$(j,l) \in (\mathbb {N}+1) \times \mathbb {Z}$
; this is trivial for
![]() $j \geq n/2$
but becomes increasingly non-trivial for smaller values of j. Then
$j \geq n/2$
but becomes increasingly non-trivial for smaller values of j. Then
where
![]() $\mathbf {j} \equiv \mathbf {Geom}(4)$
is the first component of
$\mathbf {j} \equiv \mathbf {Geom}(4)$
is the first component of
![]() $\mathbf {Hold}$
. As
$\mathbf {Hold}$
. As
![]() $\mathbf {Geom}(4)$
has exponential tail, we conclude equation (7.36) and hence Proposition 7.3, which then implies Propositions 7.1, 1.17 and Theorem 1.3.
$\mathbf {Geom}(4)$
has exponential tail, we conclude equation (7.36) and hence Proposition 7.3, which then implies Propositions 7.1, 1.17 and Theorem 1.3.
It remains to prove equation (7.37). Roughly speaking, we will accomplish this by a downward induction on j, or more precisely, by an upward induction on a quantity m, which is morally equivalent to
![]() $\lfloor n/2\rfloor - j$
. To make this more precise, it is convenient to introduce the quantities
$\lfloor n/2\rfloor - j$
. To make this more precise, it is convenient to introduce the quantities
![]() $Q_m$
for any
$Q_m$
for any
![]() $m \in [n/2]$
by the formula
$m \in [n/2]$
by the formula
Clearly we have
since
![]() $Q(j,l) \leq 1$
for all
$Q(j,l) \leq 1$
for all
![]() $j,l$
; this bound can be thought of as supplying the ‘base case’ for our induction). We trivially have
$j,l$
; this bound can be thought of as supplying the ‘base case’ for our induction). We trivially have
![]() $Q_m \geq Q_{m-1}$
for any
$Q_m \geq Q_{m-1}$
for any
![]() $1 \leq m \leq n/2$
. We will shortly establish the opposite inequality:
$1 \leq m \leq n/2$
. We will shortly establish the opposite inequality:
Proposition 7.8 (Monotonicity)
We have
whenever
![]() $C_{A,\varepsilon } \leq m \leq n/2$
for some sufficiently large
$C_{A,\varepsilon } \leq m \leq n/2$
for some sufficiently large
![]() $C_{A,\varepsilon }$
depending on
$C_{A,\varepsilon }$
depending on
![]() $A,\varepsilon $
.
$A,\varepsilon $
.
Assuming Proposition 7.8, we conclude from equation (7.39) and a (forward) induction on m that
![]() $Q_m \leq C_{A,\varepsilon }^A \ll _A 1$
for all
$Q_m \leq C_{A,\varepsilon }^A \ll _A 1$
for all
![]() $1 \leq m \leq n/2$
, which gives equation (7.37). This in turn implies Proposition 7.3, and hence Proposition 7.1, Proposition 1.17, and Theorem 1.3.
$1 \leq m \leq n/2$
, which gives equation (7.37). This in turn implies Proposition 7.3, and hence Proposition 7.1, Proposition 1.17, and Theorem 1.3.
It remains to establish Proposition (7.8). Let
![]() $C_{A,\varepsilon } \leq m \leq n/2$
for some sufficiently large
$C_{A,\varepsilon } \leq m \leq n/2$
for some sufficiently large
![]() $C_{A,\varepsilon }$
. It suffices to show that
$C_{A,\varepsilon }$
. It suffices to show that
whenever
![]() $j = \lfloor n/2 \rfloor - m$
and
$j = \lfloor n/2 \rfloor - m$
and
![]() $l \in \mathbb {Z}$
. Note from equation (7.38) that we immediately obtain
$l \in \mathbb {Z}$
. Note from equation (7.38) that we immediately obtain
![]() $Q(j,l) \leq m^{-A} Q_m$
, but to be able to use
$Q(j,l) \leq m^{-A} Q_m$
, but to be able to use
![]() $Q_{m-1}$
instead of
$Q_{m-1}$
instead of
![]() $Q_m$
, we will apply equation (7.35) at least once, in order to estimate
$Q_m$
, we will apply equation (7.35) at least once, in order to estimate
![]() $Q(j,l)$
in terms of other values
$Q(j,l)$
in terms of other values
![]() $Q(j',l')$
of Q with
$Q(j',l')$
of Q with
![]() $j'> j$
. This causes a degradation in the
$j'> j$
. This causes a degradation in the
![]() $m^{-A}$
term, even when m is large; to overcome this loss we need to ensure that (with high probability) the two-dimensional renewal process visits a sufficient number of white points before we use
$m^{-A}$
term, even when m is large; to overcome this loss we need to ensure that (with high probability) the two-dimensional renewal process visits a sufficient number of white points before we use
![]() $Q_{m-1}$
to bound the resulting expression. This is of course consistent with the interpretation of equation (7.10) as an assertion that the renewal process encounters plenty of white points.
$Q_{m-1}$
to bound the resulting expression. This is of course consistent with the interpretation of equation (7.10) as an assertion that the renewal process encounters plenty of white points.
We divide the proof of equation (7.41) into three cases. Let
![]() ${\mathcal T}$
be the family of triangles from Lemma 7.4.
${\mathcal T}$
be the family of triangles from Lemma 7.4.
Case 1:
![]() $(j,l) \in W$
. This is the easiest case, as one can immediately get a gain from the white point
$(j,l) \in W$
. This is the easiest case, as one can immediately get a gain from the white point
![]() $(j,l)$
. From equation (7.35), we have
$(j,l)$
. From equation (7.35), we have
For any
![]() $(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
, we have from equation (7.38) (applied with m replaced by
$(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
, we have from equation (7.38) (applied with m replaced by
![]() $m-1$
) that
$m-1$
) that
since
![]() $j+j' \geq j+1 = \lfloor n/2 \rfloor - (m-1)$
. Replacing
$j+j' \geq j+1 = \lfloor n/2 \rfloor - (m-1)$
. Replacing
![]() $(j',l')$
by
$(j',l')$
by
![]() $\mathbf {Hold}$
(so that
$\mathbf {Hold}$
(so that
![]() $j'$
has the distribution of
$j'$
has the distribution of
![]() $\mathbf {Geom}(4)$
) and taking expectations, we conclude that
$\mathbf {Geom}(4)$
) and taking expectations, we conclude that
We can bound
 $$ \begin{align} \max(m-r,1)^{-1} \leq m^{-1} \exp\left( O\left( \frac{r\log m}{m}\right ) \right) \end{align} $$
$$ \begin{align} \max(m-r,1)^{-1} \leq m^{-1} \exp\left( O\left( \frac{r\log m}{m}\right ) \right) \end{align} $$
for any
![]() $r \in \mathbb {N}+1$
; indeed this bound is trivial for
$r \in \mathbb {N}+1$
; indeed this bound is trivial for
![]() $r \geq m$
, and for
$r \geq m$
, and for
![]() $r < m$
one can use the concave nature of
$r < m$
one can use the concave nature of
![]() $x \mapsto \log (1-x)$
for
$x \mapsto \log (1-x)$
for
![]() $0 < x < 1$
to conclude that
$0 < x < 1$
to conclude that
 $$ \begin{align*}\frac{\log\left(1-\frac{r}{m}\right)}{r/m} \geq \frac{\log \left(1 - \frac{m-1}{m}\right)}{(m-1)/m}\end{align*} $$
$$ \begin{align*}\frac{\log\left(1-\frac{r}{m}\right)}{r/m} \geq \frac{\log \left(1 - \frac{m-1}{m}\right)}{(m-1)/m}\end{align*} $$
which rearranges to give the stated bound. Replacing r by
![]() $\mathbf {Geom}(4)$
and raising to the
$\mathbf {Geom}(4)$
and raising to the
![]() $A^{\mathrm {th}}$
power, we obtain
$A^{\mathrm {th}}$
power, we obtain
 $$ \begin{align*}Q(j,l) \leq \exp( - \varepsilon^3 ) m^{-A} Q_{m-1} \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \mathbf{Geom}(4) \right) \right).\end{align*} $$
$$ \begin{align*}Q(j,l) \leq \exp( - \varepsilon^3 ) m^{-A} Q_{m-1} \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \mathbf{Geom}(4) \right) \right).\end{align*} $$
For m large enough depending on
![]() $A,\varepsilon $
, we then have
$A,\varepsilon $
, we then have
which gives equation (7.41) in this case (with some room to spare).
Case 2:
![]() $(j,l) \in \Delta $
for some triangle
$(j,l) \in \Delta $
for some triangle
![]() $\Delta \in {\mathcal T}$
, and
$\Delta \in {\mathcal T}$
, and
![]() $l \geq l_\Delta - \frac {m}{\log ^2 m}$
. This case is slightly harder than the preceding one, as one has to walk randomly through the triangle
$l \geq l_\Delta - \frac {m}{\log ^2 m}$
. This case is slightly harder than the preceding one, as one has to walk randomly through the triangle
![]() $\Delta $
before one has a good chance to encounter a white point, but because this portion of the walk is relatively short, the degradation of the weight
$\Delta $
before one has a good chance to encounter a white point, but because this portion of the walk is relatively short, the degradation of the weight
![]() $m^{-A}$
during this portion will be negligible.
$m^{-A}$
during this portion will be negligible.
We turn to the details. Set
![]() $s := l_\Delta - l$
; thus
$s := l_\Delta - l$
; thus
![]() $0 \leq s \leq \frac {m}{\log ^2 m}$
. Let
$0 \leq s \leq \frac {m}{\log ^2 m}$
. Let
![]() $\mathbf {v} _1,\mathbf {v}_2,\dots $
be iid copies of
$\mathbf {v} _1,\mathbf {v}_2,\dots $
be iid copies of
![]() $\mathbf {Hold}$
, write
$\mathbf {Hold}$
, write
![]() $\mathbf {v}_k = (\mathbf {j}_k, \mathbf {l}_k)$
for each k with the usual summation notations in equation (1.6), and define the first passage time
$\mathbf {v}_k = (\mathbf {j}_k, \mathbf {l}_k)$
for each k with the usual summation notations in equation (1.6), and define the first passage time
![]() $\mathbf {k} \in \mathbb {N}+1$
to be the least positive integer such that
$\mathbf {k} \in \mathbb {N}+1$
to be the least positive integer such that
This is a finite random variable since the
![]() $\mathbf {l}_k$
are all positive integers. Heuristically,
$\mathbf {l}_k$
are all positive integers. Heuristically,
![]() $\mathbf {k}$
represents the time in which the sequence first exits the triangle
$\mathbf {k}$
represents the time in which the sequence first exits the triangle
![]() $\Delta $
, assuming that this exit occurs on the top edge of the triangle. It is in principle possible for the sequence to instead exit
$\Delta $
, assuming that this exit occurs on the top edge of the triangle. It is in principle possible for the sequence to instead exit
![]() $\Delta $
through the hypotenuse of the triangle, in which case
$\Delta $
through the hypotenuse of the triangle, in which case
![]() $\mathbf {k}$
will be somewhat larger than the first exit time; however, as we shall see below, the Chernoff bound in Lemma 7.7 can be used to show that the former scenario will occur with probability
$\mathbf {k}$
will be somewhat larger than the first exit time; however, as we shall see below, the Chernoff bound in Lemma 7.7 can be used to show that the former scenario will occur with probability
![]() $\gg 1$
, which will be sufficient for the purposes of establishing equation (7.41) in this case.
$\gg 1$
, which will be sufficient for the purposes of establishing equation (7.41) in this case.
By iterating equation (7.35) appropriately (or using equation (7.34)), we have the identity
 $$ \begin{align} Q(j,l) = \mathbb{E} \left[ \exp\left( - \varepsilon^3 \sum_{i=0}^{\mathbf{k}-1} 1_W((j,l) + \mathbf{v}_{[1,i]}) \right) Q((j,l) + \mathbf{v} _{[1,\mathbf{k}]}) \right] \end{align} $$
$$ \begin{align} Q(j,l) = \mathbb{E} \left[ \exp\left( - \varepsilon^3 \sum_{i=0}^{\mathbf{k}-1} 1_W((j,l) + \mathbf{v}_{[1,i]}) \right) Q((j,l) + \mathbf{v} _{[1,\mathbf{k}]}) \right] \end{align} $$
and hence by equation (7.38)
 $$ \begin{align*}Q(j,l) \leq Q_{m-1} \mathbb{E} \left[ \exp\left( - \frac{\varepsilon^3}{2} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}]}) \right) \max(m - \mathbf{j}_{[1,\mathbf{k}]},1)^{-A}\right]\end{align*} $$
$$ \begin{align*}Q(j,l) \leq Q_{m-1} \mathbb{E} \left[ \exp\left( - \frac{\varepsilon^3}{2} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}]}) \right) \max(m - \mathbf{j}_{[1,\mathbf{k}]},1)^{-A}\right]\end{align*} $$
which by equation (7.42) gives
 $$ \begin{align*}Q(j,l) \leq m^{-A} Q_{m-1} \mathbb{E} \exp\left( - \frac{\varepsilon^3}{2} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}]})\right) \exp\left( O\left( \frac{A \log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right)\right).\end{align*} $$
$$ \begin{align*}Q(j,l) \leq m^{-A} Q_{m-1} \mathbb{E} \exp\left( - \frac{\varepsilon^3}{2} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}]})\right) \exp\left( O\left( \frac{A \log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right)\right).\end{align*} $$
To prove equation (7.41) in this case, it thus suffices to show that
 $$ \begin{align} \mathbb{E} \exp\left( - \frac{\varepsilon^3}{2} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}]}) \right) \exp\left( O\left( \frac{A \log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right)\right) \leq 1. \end{align} $$
$$ \begin{align} \mathbb{E} \exp\left( - \frac{\varepsilon^3}{2} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}]}) \right) \exp\left( O\left( \frac{A \log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right)\right) \leq 1. \end{align} $$
Since
![]() $\exp (-\varepsilon ^3/2) \leq 1 - \varepsilon ^3/4$
, we can upper bound the left-hand side by
$\exp (-\varepsilon ^3/2) \leq 1 - \varepsilon ^3/4$
, we can upper bound the left-hand side by
 $$ \begin{align} \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right) \right) - \frac{\varepsilon^3}{4} \mathbb{P}( (j,l) + \mathbf{v} _{[1,\mathbf{k}]} \in W ). \end{align} $$
$$ \begin{align} \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right) \right) - \frac{\varepsilon^3}{4} \mathbb{P}( (j,l) + \mathbf{v} _{[1,\mathbf{k}]} \in W ). \end{align} $$
We begin by controlling the first term on the right-hand side of equation (7.47). By definition, the first passage location
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
takes values in the region
$(j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
takes values in the region
![]() $\{ (j',l') \in \mathbb {Z}^2: j'> j, l' > l_\Delta \}$
. From Lemma 7.7, we have
$\{ (j',l') \in \mathbb {Z}^2: j'> j, l' > l_\Delta \}$
. From Lemma 7.7, we have
 $$ \begin{align} \mathbb{P}( (j,l) + \mathbf{v}_{[1,\mathbf{k}]} = (j',l') ) \ll \frac{e^{-c(l'-l_\Delta)}}{(1+s)^{1/2} } G_{1+s}\left(c\left(j'-j - \frac{s}{4}\right) \right). \end{align} $$
$$ \begin{align} \mathbb{P}( (j,l) + \mathbf{v}_{[1,\mathbf{k}]} = (j',l') ) \ll \frac{e^{-c(l'-l_\Delta)}}{(1+s)^{1/2} } G_{1+s}\left(c\left(j'-j - \frac{s}{4}\right) \right). \end{align} $$
Summing in
![]() $l'$
, we conclude that
$l'$
, we conclude that
for any
![]() $j'$
; informally,
$j'$
; informally,
![]() $\mathbf {j}_{[1,\mathbf {k}]}$
is behaving like a Gaussian random variable centred at
$\mathbf {j}_{[1,\mathbf {k}]}$
is behaving like a Gaussian random variable centred at
![]() $s/4$
with standard deviation
$s/4$
with standard deviation
![]() $\asymp (1+s)^{1/2}$
. In particular, because of the hypothesis
$\asymp (1+s)^{1/2}$
. In particular, because of the hypothesis
![]() $s \leq \frac {m}{\log ^2 m}$
, we have
$s \leq \frac {m}{\log ^2 m}$
, we have
when
![]() $r> \frac {m}{\log ^2 m}$
(say). With our hypotheses
$r> \frac {m}{\log ^2 m}$
(say). With our hypotheses
![]() $s \leq \frac {m}{\log ^2 m}$
and
$s \leq \frac {m}{\log ^2 m}$
and
![]() $m \geq C_{A,\varepsilon }$
, the quantity
$m \geq C_{A,\varepsilon }$
, the quantity
![]() $\frac {A \log m}{m}$
is much smaller than
$\frac {A \log m}{m}$
is much smaller than
![]() $1$
, and by using the above bound to control the contribution when
$1$
, and by using the above bound to control the contribution when
![]() $\mathbf {j}_{[1,\mathbf {k}]}> \frac {m}{\log ^2 m}$
, we have
$\mathbf {j}_{[1,\mathbf {k}]}> \frac {m}{\log ^2 m}$
, we have
 $$ \begin{align} \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right) \right) &\leq \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \frac{m}{\log^2 m} \right) \right) + O\left( \exp\left( - c \frac{m}{\log^2 m} \right) \right)\nonumber\\ = 1 + O\left( \frac{A}{\log m} \right). \end{align} $$
$$ \begin{align} \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \mathbf{j}_{[1,\mathbf{k}]} \right) \right) &\leq \mathbb{E} \exp\left( O\left( \frac{A\log m}{m} \frac{m}{\log^2 m} \right) \right) + O\left( \exp\left( - c \frac{m}{\log^2 m} \right) \right)\nonumber\\ = 1 + O\left( \frac{A}{\log m} \right). \end{align} $$
Now we turn attention to the second term on the right-hand side of equation (7.47). Using equation (7.48) to handle all points
![]() $(j',l')$
outside the region
$(j',l')$
outside the region
![]() $l' = l_\Delta +O(1)$
and
$l' = l_\Delta +O(1)$
and
![]() $j' = j + \frac {s}{4} + O( (1+s)^{1/2} )$
, we have
$j' = j + \frac {s}{4} + O( (1+s)^{1/2} )$
, we have
for a suitable choice of implied constants in the O-notation that is independent of
![]() $\varepsilon $
(cf. equation (7.31)). On the other hand, since
$\varepsilon $
(cf. equation (7.31)). On the other hand, since
![]() $(j,l) \in \Delta $
and
$(j,l) \in \Delta $
and
![]() $s = l_\Delta - l$
, we have from equation (7.11) that
$s = l_\Delta - l$
, we have from equation (7.11) that
and thus (since
![]() $0 < \frac {1}{4} \log 9 < \log 2$
) one has
$0 < \frac {1}{4} \log 9 < \log 2$
) one has
whenever
![]() $j' = j + \frac {s}{4} + O((1+s)^{1/2})$
, with the implied constants independent of
$j' = j + \frac {s}{4} + O((1+s)^{1/2})$
, with the implied constants independent of
![]() $\varepsilon $
. We conclude that with probability
$\varepsilon $
. We conclude that with probability
![]() $\gg 1$
, the first passage location
$\gg 1$
, the first passage location
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
lies outside of
$(j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
lies outside of
![]() $\Delta $
, but at a distance
$\Delta $
, but at a distance
![]() $O(1)$
from
$O(1)$
from
![]() $\Delta $
, hence is white by Lemma 7.4. We conclude that
$\Delta $
, hence is white by Lemma 7.4. We conclude that
and equation (7.41) (and hence equation (7.46)) now follows from equations (7.47), (7.49) and (7.51) since
![]() $m \geq C_{A,\varepsilon }$
.
$m \geq C_{A,\varepsilon }$
.
Case 3:
![]() $(j,l) \in \Delta $
for some triangle
$(j,l) \in \Delta $
for some triangle
![]() $\Delta \in {\mathcal T}$
, and
$\Delta \in {\mathcal T}$
, and
![]() $l < l_\Delta - \frac {m}{\log ^2 m}$
. This is the most difficult case, as one has to walk so far before exiting
$l < l_\Delta - \frac {m}{\log ^2 m}$
. This is the most difficult case, as one has to walk so far before exiting
![]() $\Delta $
that one needs to encounter multiple white points, not just a single white point, in order to counteract the degradation of the weight
$\Delta $
that one needs to encounter multiple white points, not just a single white point, in order to counteract the degradation of the weight
![]() $m^{-A}$
. Fortunately, the number of white points one needs to encounter is
$m^{-A}$
. Fortunately, the number of white points one needs to encounter is
![]() $O_{A,\varepsilon }(1)$
, and we will be able to locate such a number of white points on average for m large enough.
$O_{A,\varepsilon }(1)$
, and we will be able to locate such a number of white points on average for m large enough.
We will need a large constant P (much larger than A or
![]() $1/\varepsilon $
, but much smaller than m) depending on
$1/\varepsilon $
, but much smaller than m) depending on
![]() $A,\varepsilon $
to be chosen later; the implied constants in the asymptotic notation below will not depend on P unless otherwise specified. As before, we set
$A,\varepsilon $
to be chosen later; the implied constants in the asymptotic notation below will not depend on P unless otherwise specified. As before, we set
![]() $s := l_\Delta - l$
, so now
$s := l_\Delta - l$
, so now
![]() $s> \frac {m}{\log ^2 m}$
. From equation (7.11), we have
$s> \frac {m}{\log ^2 m}$
. From equation (7.11), we have
, while from Lemma 7.4, one has
![]() $j_\Delta + \frac {s_\Delta }{\log 9} \leq \lfloor \frac {n}{2} \rfloor \leq j+m$
, hence
$j_\Delta + \frac {s_\Delta }{\log 9} \leq \lfloor \frac {n}{2} \rfloor \leq j+m$
, hence
We again let
![]() $\mathbf {v}_1,\mathbf {v}_2,\dots $
be iid copies of
$\mathbf {v}_1,\mathbf {v}_2,\dots $
be iid copies of
![]() $\mathbf {Hold}$
, write
$\mathbf {Hold}$
, write
![]() $\mathbf {v}_k = (\mathbf {j}_k, \mathbf {l}_k)$
for each k, and define the first passage time
$\mathbf {v}_k = (\mathbf {j}_k, \mathbf {l}_k)$
for each k, and define the first passage time
![]() $\mathbf {k} \in \mathbb {N}+1$
to be the least positive integer such that equation (7.44) holds. From equation (7.45), we have
$\mathbf {k} \in \mathbb {N}+1$
to be the least positive integer such that equation (7.44) holds. From equation (7.45), we have
Applying equation (7.35), we then have
 $$ \begin{align} Q(j,l) \leq \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \right) Q((j,l) + \mathbf{v} _{[1,\mathbf{k}+P]}). \end{align} $$
$$ \begin{align} Q(j,l) \leq \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \right) Q((j,l) + \mathbf{v} _{[1,\mathbf{k}+P]}). \end{align} $$
Applying equation (7.38) to
![]() $Q((j,l) + \mathbf {v}_{[1,\mathbf {k}+P]}) = Q(j+\mathbf {j}_{[1,\mathbf {k}+P]}, l+\mathbf {l}_{[1,\mathbf {k}+P]})$
, we have
$Q((j,l) + \mathbf {v}_{[1,\mathbf {k}+P]}) = Q(j+\mathbf {j}_{[1,\mathbf {k}+P]}, l+\mathbf {l}_{[1,\mathbf {k}+P]})$
, we have
(since
![]() $j + \mathbf {j}_{[1,\mathbf {k}+P]} \geq j+1 \geq \lfloor n/2 \rfloor - (m-1)$
). We can rearrange this inequality as
$j + \mathbf {j}_{[1,\mathbf {k}+P]} \geq j+1 \geq \lfloor n/2 \rfloor - (m-1)$
). We can rearrange this inequality as
 $$ \begin{align*}Q((j,l) + \mathbf{v}_{[1,\mathbf{k}+P]}) \leq m^{-A} Q_{m-1} \max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A};\end{align*} $$
$$ \begin{align*}Q((j,l) + \mathbf{v}_{[1,\mathbf{k}+P]}) \leq m^{-A} Q_{m-1} \max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A};\end{align*} $$
inserting this back into equation (7.53), we conclude that
 $$ \begin{align*}Q(j,l) \leq m^{-A} Q_{m-1} \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}) \right) \max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A}. \end{align*} $$
$$ \begin{align*}Q(j,l) \leq m^{-A} Q_{m-1} \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}) \right) \max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A}. \end{align*} $$
Thus, to establish equation (7.41) in this case, it suffices to show that
 $$ \begin{align} \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} )\right) \max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A} \leq 1. \end{align} $$
$$ \begin{align} \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} )\right) \max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A} \leq 1. \end{align} $$
Let us first consider the event that
![]() $\mathbf {j}_{[1,\mathbf {k}+P]} \geq 0.9 m$
. From Lemma 7.7 and the bound in equation (7.52), we have
$\mathbf {j}_{[1,\mathbf {k}+P]} \geq 0.9 m$
. From Lemma 7.7 and the bound in equation (7.52), we have
(noting that
![]() $0.8> \frac {1}{4} \frac {\log 9}{\log 2}$
) while from Lemma 2.2 (recalling that the
$0.8> \frac {1}{4} \frac {\log 9}{\log 2}$
) while from Lemma 2.2 (recalling that the
![]() $\mathbf {j}_k$
are iid copies of
$\mathbf {j}_k$
are iid copies of
![]() $\mathbf {Geom}(4)$
), we have
$\mathbf {Geom}(4)$
), we have
and thus by the triangle inequality
Thus the contribution of this case to equation (7.54) is
![]() $O_{P,A}(m^A \exp (-cm)) = O_{P,A}(\exp (-cm/2))$
. If instead we have
$O_{P,A}(m^A \exp (-cm)) = O_{P,A}(\exp (-cm/2))$
. If instead we have
![]() $\mathbf {j}_{[1,\mathbf {k}+P]} < 0.9 m$
, then
$\mathbf {j}_{[1,\mathbf {k}+P]} < 0.9 m$
, then
 $$ \begin{align*}\max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A} \leq 10^A.\end{align*} $$
$$ \begin{align*}\max\left( 1 - \frac{\mathbf{j}_{[1,\mathbf{k}+P]}}{m}, \frac{1}{m}\right)^{-A} \leq 10^A.\end{align*} $$
Since m is large compared to
![]() $A,P$
, to show equation (7.54) it thus suffices to show that
$A,P$
, to show equation (7.54) it thus suffices to show that
 $$ \begin{align} \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} )\right) \leq 10^{-A-1}. \end{align} $$
$$ \begin{align} \mathbb{E} \exp\left( - \varepsilon^3 \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} )\right) \leq 10^{-A-1}. \end{align} $$
Since the left-hand side of equation (7.55) is at most
 $$ \begin{align*}\mathbb{P}\left( \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \leq \frac{10 A}{\varepsilon^3} \right) + \exp(-10A),\end{align*} $$
$$ \begin{align*}\mathbb{P}\left( \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \leq \frac{10 A}{\varepsilon^3} \right) + \exp(-10A),\end{align*} $$
it will suffice to establish the bound
 $$ \begin{align} \mathbb{P}\left( \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \leq \frac{10 A}{\varepsilon^3} \right) \leq 10^{-A-2} \end{align} $$
$$ \begin{align} \mathbb{P}\left( \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \leq \frac{10 A}{\varepsilon^3} \right) \leq 10^{-A-2} \end{align} $$
(say).
Roughly speaking, the estimate in equation (7.56) asserts that once one exits the large triangle
![]() $\Delta $
, then one should almost always encounter at least
$\Delta $
, then one should almost always encounter at least
![]() $10A/\varepsilon ^3$
white points by a certain time
$10A/\varepsilon ^3$
white points by a certain time
![]() $P = O_{A,\varepsilon }(1)$
.
$P = O_{A,\varepsilon }(1)$
.
To prove equation (7.56), we introduce another random statistic that measures the number of triangles that one encounters on an infinite two-dimensional renewal process
![]() $(j',l'), (j',l') + \mathbf {v}_1, (j',l') + \mathbf {v} _{[1,2]},\dots $
, where
$(j',l'), (j',l') + \mathbf {v}_1, (j',l') + \mathbf {v} _{[1,2]},\dots $
, where
![]() $(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
and
$(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
and
![]() $\mathbf {v}_1,\mathbf {v}_2,\dots $
are iid copies of
$\mathbf {v}_1,\mathbf {v}_2,\dots $
are iid copies of
![]() $\mathbf {Hold}$
. (We will eventually set
$\mathbf {Hold}$
. (We will eventually set
![]() $(j',l') := (j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
, so that the above renewal process is identical in distribution to
$(j',l') := (j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
, so that the above renewal process is identical in distribution to
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
,
$(j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
,
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+1]}$
,
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+1]}$
,
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+2]}, \dots $
.)
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+2]}, \dots $
.)
Given an initial point
![]() $(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
, we recursively introduce the stopping times
$(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
, we recursively introduce the stopping times
![]() $\mathbf {t}_1 = \mathbf {t}_1(j',l'),\dots ,\mathbf {t}_{\mathbf {r}} = \mathbf {t}_{\mathbf {r}(j',l')}(j,l)$
by defining
$\mathbf {t}_1 = \mathbf {t}_1(j',l'),\dots ,\mathbf {t}_{\mathbf {r}} = \mathbf {t}_{\mathbf {r}(j',l')}(j,l)$
by defining
![]() $\mathbf {t}_1$
to be the first natural number (if it exists) for which
$\mathbf {t}_1$
to be the first natural number (if it exists) for which
![]() $(j',l') + \mathbf {v}_{[1,\mathbf {t}_1]}$
lies in a triangle
$(j',l') + \mathbf {v}_{[1,\mathbf {t}_1]}$
lies in a triangle
![]() $\mathbf {\Delta }_1 \in {\mathcal T}$
, then for each
$\mathbf {\Delta }_1 \in {\mathcal T}$
, then for each
![]() $i>1$
, defining
$i>1$
, defining
![]() $\mathbf {t}_i$
to be the first natural number (if it exists) with
$\mathbf {t}_i$
to be the first natural number (if it exists) with
![]() $l' + \mathbf {l}_{[1,\mathbf {t}_i]}> l_{\mathbf {\Delta }_{i-1}}$
and
$l' + \mathbf {l}_{[1,\mathbf {t}_i]}> l_{\mathbf {\Delta }_{i-1}}$
and
![]() $(j',l') + \mathbf {v}_{[1,\mathbf {t}_i]}$
lies in a triangle
$(j',l') + \mathbf {v}_{[1,\mathbf {t}_i]}$
lies in a triangle
![]() $\mathbf {\Delta }_i \in {\mathcal T}$
. We set
$\mathbf {\Delta }_i \in {\mathcal T}$
. We set
![]() $\mathbf {r} = \mathbf {r}(j',l')$
to be the number of stopping times that can be constructed in this fashion (thus, there are no natural numbers k with
$\mathbf {r} = \mathbf {r}(j',l')$
to be the number of stopping times that can be constructed in this fashion (thus, there are no natural numbers k with
![]() $l + \mathbf {l}_{[1,k]}> l_{\mathbf {\Delta }_{\mathbf {r}}}$
and
$l + \mathbf {l}_{[1,k]}> l_{\mathbf {\Delta }_{\mathbf {r}}}$
and
![]() $(j',l') + \mathbf {v}_{[1,k]}$
black). Note that
$(j',l') + \mathbf {v}_{[1,k]}$
black). Note that
![]() $\mathbf {r}$
is finite since the process
$\mathbf {r}$
is finite since the process
![]() $(j',l')+\mathbf {v}_{[1,k]}$
eventually exits the strip
$(j',l')+\mathbf {v}_{[1,k]}$
eventually exits the strip
![]() $[n/2] \times \mathbb {Z}$
when k is large enough, at which point it no longer encounters any black triangles.
$[n/2] \times \mathbb {Z}$
when k is large enough, at which point it no longer encounters any black triangles.
The key estimate relating
![]() $\mathbf {r}$
with the expression in equation (7.56) is then
$\mathbf {r}$
with the expression in equation (7.56) is then
Lemma 7.9 (Many triangles usually implies many white points)
Let
![]() $\mathbf {v}_1,\mathbf {v}_2,\dots $
be iid copies of
$\mathbf {v}_1,\mathbf {v}_2,\dots $
be iid copies of
![]() $\mathbf {Hold}$
. Then for any
$\mathbf {Hold}$
. Then for any
![]() $(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
and any positive integer R, we have
$(j',l') \in (\mathbb {N}+1) \times \mathbb {Z}$
and any positive integer R, we have
 $$ \begin{align} \mathbb{E} \exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j',l') + \mathbf{v}_{[1,p]}) + \varepsilon \min(\mathbf{r},R) \right) \leq \exp(\varepsilon), \end{align} $$
$$ \begin{align} \mathbb{E} \exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j',l') + \mathbf{v}_{[1,p]}) + \varepsilon \min(\mathbf{r},R) \right) \leq \exp(\varepsilon), \end{align} $$
where
![]() $0 < \varepsilon < 1/100$
is the sufficiently small absolute constant that has been in use throughout this section.
$0 < \varepsilon < 1/100$
is the sufficiently small absolute constant that has been in use throughout this section.
Informally the estimate in equation (7.57) asserts that when
![]() $\mathbf {r}$
is large (so that the renewal process
$\mathbf {r}$
is large (so that the renewal process
![]() $(j',l'), (j',l') + \mathbf {v}_1, (j',l') + \mathbf {v}_{[1,2]},\dots $
passes through many different triangles), then the quantity
$(j',l'), (j',l') + \mathbf {v}_1, (j',l') + \mathbf {v}_{[1,2]},\dots $
passes through many different triangles), then the quantity
![]() $\sum _{p=1}^{\mathbf {t}_{\min (\mathbf {r},R)}} 1_W((j',l') + \mathbf {v}_{[1,p]}$
is usually also large, implying that the same renewal process also visits many white points. This is basically due to the separation between triangles that is given by Lemma 7.4.
$\sum _{p=1}^{\mathbf {t}_{\min (\mathbf {r},R)}} 1_W((j',l') + \mathbf {v}_{[1,p]}$
is usually also large, implying that the same renewal process also visits many white points. This is basically due to the separation between triangles that is given by Lemma 7.4.
Proof. Denote the quantity on the left-hand side of equation (7.57) by
![]() $Z( (j',l'), R )$
. We induct on R. The case
$Z( (j',l'), R )$
. We induct on R. The case
![]() $R=1$
is trivial, so suppose
$R=1$
is trivial, so suppose
![]() $R \geq 2$
and that we have already established that
$R \geq 2$
and that we have already established that
for all
![]() $(j'',l'') \in (\mathbb {N}+1) \times \mathbb {Z}$
. If
$(j'',l'') \in (\mathbb {N}+1) \times \mathbb {Z}$
. If
![]() $\mathbf {r}=0$
, then we can bound
$\mathbf {r}=0$
, then we can bound
 $$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j',l') + \mathbf{v}_{[1,p]} ) + \varepsilon \min(\mathbf{r},R) \right) \leq 1.\end{align*} $$
$$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j',l') + \mathbf{v}_{[1,p]} ) + \varepsilon \min(\mathbf{r},R) \right) \leq 1.\end{align*} $$
Suppose that
![]() $\mathbf {r} \neq 0$
, so that the first stopping time
$\mathbf {r} \neq 0$
, so that the first stopping time
![]() $\mathbf {t}_1$
and triangle
$\mathbf {t}_1$
and triangle
![]() $\mathbf {\Delta }_1$
exists. Let
$\mathbf {\Delta }_1$
exists. Let
![]() $\mathbf {k}_1$
be the first natural number for which
$\mathbf {k}_1$
be the first natural number for which
![]() $l' + \mathbf {l}_{[1,\mathbf {k}_1]}> l_{\Delta _1}$
; then
$l' + \mathbf {l}_{[1,\mathbf {k}_1]}> l_{\Delta _1}$
; then
![]() $\mathbf {k}_1$
is well-defined (since we have an infinite number of
$\mathbf {k}_1$
is well-defined (since we have an infinite number of
![]() $\mathbf {l}_k$
, all of which are at least
$\mathbf {l}_k$
, all of which are at least
![]() $2$
) and
$2$
) and
![]() $\mathbf {k}_1> \mathbf {t}_1$
. The conditional expectation of
$\mathbf {k}_1> \mathbf {t}_1$
. The conditional expectation of
![]() $\exp ( - \sum _{p=1}^{\mathbf {t}_{\min (\mathbf {r},R)}} 1_W((j',l') + \mathbf {v}_{[1,p]} ) + \varepsilon \min (\mathbf {r},R))$
relative to the random variables
$\exp ( - \sum _{p=1}^{\mathbf {t}_{\min (\mathbf {r},R)}} 1_W((j',l') + \mathbf {v}_{[1,p]} ) + \varepsilon \min (\mathbf {r},R))$
relative to the random variables
![]() $\mathbf {v}_1,\dots ,\mathbf {v}_{\mathbf {k}_1}$
is equal to
$\mathbf {v}_1,\dots ,\mathbf {v}_{\mathbf {k}_1}$
is equal to
 $$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{k}_1} 1_W((j',l') + \mathbf{v}_{[1,p]} ) + \varepsilon \right) Z( 1_W((j',l') + \mathbf{v} _{[1,\mathbf{k}_1]}, R-1)\end{align*} $$
$$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{k}_1} 1_W((j',l') + \mathbf{v}_{[1,p]} ) + \varepsilon \right) Z( 1_W((j',l') + \mathbf{v} _{[1,\mathbf{k}_1]}, R-1)\end{align*} $$
which we can upper bound using the inductive hypothesis in equation (7.58) as
We thus obtain the inequality
so to close the induction it suffices to show that
Since the left-hand side is equal to
and
![]() $\varepsilon>0$
is a sufficiently small absolute constant, it will thus suffice to establish the bound
$\varepsilon>0$
is a sufficiently small absolute constant, it will thus suffice to establish the bound
For each
![]() $p \in \mathbb {N}+1$
, triangle
$p \in \mathbb {N}+1$
, triangle
![]() $\Delta _1 \in {\mathcal T}$
, and
$\Delta _1 \in {\mathcal T}$
, and
![]() $(j'',l'') \in \Delta _1$
, let
$(j'',l'') \in \Delta _1$
, let
![]() $E_{p,\Delta _1,(j'',l'')}$
denote the event that
$E_{p,\Delta _1,(j'',l'')}$
denote the event that
![]() $(j',l') + \mathbf {v}_{[1,p]} = (j'',l'')$
, and
$(j',l') + \mathbf {v}_{[1,p]} = (j'',l'')$
, and
![]() $(j',l') + \mathbf {v} _{[1,p']} \in W$
for all
$(j',l') + \mathbf {v} _{[1,p']} \in W$
for all
![]() $1 \leq p' < p$
. Observe that the event
$1 \leq p' < p$
. Observe that the event
![]() $\mathbf {r} \neq 0$
is the disjoint union of the events
$\mathbf {r} \neq 0$
is the disjoint union of the events
![]() $E_{p,\Delta _1,(j'',l'')}$
. It therefore suffices to show that
$E_{p,\Delta _1,(j'',l'')}$
. It therefore suffices to show that
We may of course assume that the event
![]() $E_{p,\Delta _1,(j'',l'')}$
occurs with non-zero probability. Conditioning to this event, we see that
$E_{p,\Delta _1,(j'',l'')}$
occurs with non-zero probability. Conditioning to this event, we see that
![]() $(j',l') + \mathbf {v}_{[1,\mathbf {k}_1]}$
has the same distribution as (the unconditioned random variable)
$(j',l') + \mathbf {v}_{[1,\mathbf {k}_1]}$
has the same distribution as (the unconditioned random variable)
![]() $(j'',l'') + \mathbf {v}_{[1,\mathbf {k}'']}$
, where the first passage time
$(j'',l'') + \mathbf {v}_{[1,\mathbf {k}'']}$
, where the first passage time
![]() $\mathbf {k}''$
is the first natural number for which
$\mathbf {k}''$
is the first natural number for which
![]() $l'' + \mathbf {l}_{[1,\mathbf {k}'']}> l_{\Delta _1}$
. By repeating the proof of equation (7.51), one has
$l'' + \mathbf {l}_{[1,\mathbf {k}'']}> l_{\Delta _1}$
. By repeating the proof of equation (7.51), one has
giving equation (7.59). This establishes the lemma.
To use this bound we need to show that the renewal process
![]() $(j,l)+\mathbf {v}_{[1,\mathbf {k}]}, (j,l) + \mathbf {v}_{[1,\mathbf{k}+1]}, (j,l) + \mathbf {v}_{[1,\mathbf {k}+2]},\dots $
passes either through many white points or through many triangles. This will be established via a probabilistic upper bound on the size
$(j,l)+\mathbf {v}_{[1,\mathbf {k}]}, (j,l) + \mathbf {v}_{[1,\mathbf{k}+1]}, (j,l) + \mathbf {v}_{[1,\mathbf {k}+2]},\dots $
passes either through many white points or through many triangles. This will be established via a probabilistic upper bound on the size
![]() $s_\Delta $
of the triangles encountered. The key lemma in this regard is
$s_\Delta $
of the triangles encountered. The key lemma in this regard is
Lemma 7.10 (Large triangles are rarely encountered shortly after a lengthy crossing)
Let
![]() $(j,l)$
be an element of a black triangle
$(j,l)$
be an element of a black triangle
![]() $\Delta $
with
$\Delta $
with
![]() $s := l_\Delta - l$
obeying
$s := l_\Delta - l$
obeying
![]() $s> \frac {m}{\log ^2 m}$
(where we recall
$s> \frac {m}{\log ^2 m}$
(where we recall
![]() $m = \lfloor n/2\rfloor - j$
), and let
$m = \lfloor n/2\rfloor - j$
), and let
![]() $\mathbf {k}$
be the first passage time associated to s defined in Lemma 7.7. Let
$\mathbf {k}$
be the first passage time associated to s defined in Lemma 7.7. Let
![]() $p \in \mathbb {N}$
and
$p \in \mathbb {N}$
and
![]() $1 \leq s' \leq m^{0.4}$
. Let
$1 \leq s' \leq m^{0.4}$
. Let
![]() $E_{p,s'}$
denote the event that
$E_{p,s'}$
denote the event that
![]() $(j,l) + \mathbf {v} _{[1,\mathbf {k}+p]}$
lies in a triangle
$(j,l) + \mathbf {v} _{[1,\mathbf {k}+p]}$
lies in a triangle
![]() $\Delta ' \in {\mathcal T}$
of size
$\Delta ' \in {\mathcal T}$
of size
![]() $s_{\Delta '} \geq s'$
. Then
$s_{\Delta '} \geq s'$
. Then
As in the rest of this section, we stress that the implied constants in our asymptotic notation are uniform in n and
![]() $\xi $
.
$\xi $
.
Proof. We can assume that
for a large constant C, since the claim is trivial otherwise.
From Lemma 7.7, we have equation (7.48) as before, so on summing in
![]() $j'$
, we have
$j'$
, we have
and thus
Similarly, from Lemma 2.2, one has
and thus
In a similar spirit, from equation (7.48) and summing in
![]() $l'$
one has
$l'$
one has
so in particular
from the upper bound on
![]() $s'$
. From Lemma 2.2, we also have
$s'$
. From Lemma 2.2, we also have
and hence
Thus, if
![]() $E'$
denotes the event that
$E'$
denotes the event that
![]() $l + \mathbf {l}_{[1,\mathbf {k}+p]} \geq l_\Delta + 2A^2 (1+p)$
or
$l + \mathbf {l}_{[1,\mathbf {k}+p]} \geq l_\Delta + 2A^2 (1+p)$
or
![]() $|\mathbf {j}_{[1,\mathbf {k}+p]} - \frac {s}{4}| \geq 2s^{0.6}$
, then
$|\mathbf {j}_{[1,\mathbf {k}+p]} - \frac {s}{4}| \geq 2s^{0.6}$
, then
We will devote the rest of the proof to establishing the complementary estimate
which together with equation (7.61) implies the lemma.
Suppose now that we are outside the event
![]() $E'$
, and that
$E'$
, and that
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies in a triangle
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies in a triangle
![]() $\Delta '$
; thus
$\Delta '$
; thus
and
thanks to equation (7.52). From equation (7.11), we then have
Suppose that the lower tip of
![]() $\Delta '$
lies well below the upper edge of
$\Delta '$
lies well below the upper edge of
![]() $\Delta $
in the sense that
$\Delta $
in the sense that
Then by equation (7.63), we can find an integer
![]() $j' = j+\mathbf {j}_{[1,\mathbf {k}+p]} + O( A^2 (1+p) )$
such that
$j' = j+\mathbf {j}_{[1,\mathbf {k}+p]} + O( A^2 (1+p) )$
such that
![]() $j' \geq j_{\Delta '}$
and
$j' \geq j_{\Delta '}$
and
In other words,
![]() $(j',l_\Delta ) \in \Delta '$
. But by equation (7.64), we have
$(j',l_\Delta ) \in \Delta '$
. But by equation (7.64), we have
From equation (7.11), we have
and hence (since
![]() $s \geq \frac {m}{\log ^2 m}$
and
$s \geq \frac {m}{\log ^2 m}$
and
![]() $\frac {1}{4} \log 9 < \log 2$
)
$\frac {1}{4} \log 9 < \log 2$
)
Thus
![]() $(j',l_\Delta ) \in \Delta $
. Thus
$(j',l_\Delta ) \in \Delta $
. Thus
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta '$
intersect, which by Lemma 7.4 forces
$\Delta '$
intersect, which by Lemma 7.4 forces
![]() $\Delta =\Delta '$
, which is absurd since
$\Delta =\Delta '$
, which is absurd since
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies in
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies in
![]() $\Delta '$
but not
$\Delta '$
but not
![]() $\Delta $
(the l coordinate is larger than
$\Delta $
(the l coordinate is larger than
![]() $l_\Delta $
). We conclude that
$l_\Delta $
). We conclude that
On the other hand, from equation (7.11), we have
hence by equation (7.63), we have
From equations (7.65), (7.66) and (7.63), we then have
 $$ \begin{align*} 0 \leq j + \mathbf{j}_{[1,\mathbf{k}+p]} - j_{\Delta'} &\leq \frac{1}{\log 9} s_{\Delta'} - \frac{\log 2}{\log 9} (l_{\Delta'} - l - \mathbf{l}_{[1,\mathbf{k}+p]}) \\ &= -\frac{\log 2}{\log 9} (l_\Delta - l - \mathbf{l}_{[1,\mathbf{k}+p]} + O(A^2(1+p)) ) \\ &= O( A^2 (1+p) ) \end{align*} $$
$$ \begin{align*} 0 \leq j + \mathbf{j}_{[1,\mathbf{k}+p]} - j_{\Delta'} &\leq \frac{1}{\log 9} s_{\Delta'} - \frac{\log 2}{\log 9} (l_{\Delta'} - l - \mathbf{l}_{[1,\mathbf{k}+p]}) \\ &= -\frac{\log 2}{\log 9} (l_\Delta - l - \mathbf{l}_{[1,\mathbf{k}+p]} + O(A^2(1+p)) ) \\ &= O( A^2 (1+p) ) \end{align*} $$
so that
Thus, outside the event
![]() $E'$
, the event that
$E'$
, the event that
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies in a triangle
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies in a triangle
![]() $\Delta '$
can only occur if
$\Delta '$
can only occur if
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies within a distance
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
lies within a distance
![]() $O(A^2(1+p))$
of the point
$O(A^2(1+p))$
of the point
![]() $(j_{\Delta '}, l_\Delta )$
.
$(j_{\Delta '}, l_\Delta )$
.
Now suppose we have two distinct triangles
![]() $\Delta ', \Delta ''$
in
$\Delta ', \Delta ''$
in
![]() ${\mathcal T}$
obeying equation (7.66), with
${\mathcal T}$
obeying equation (7.66), with
![]() $s_{\Delta '}, s_{\Delta ''} \geq s'$
with
$s_{\Delta '}, s_{\Delta ''} \geq s'$
with
![]() $j_{\Delta '} \leq j_{\Delta ''}$
. Set
$j_{\Delta '} \leq j_{\Delta ''}$
. Set
![]() $l_* := l_\Delta + \lfloor s'/2 \rfloor $
, and observe from equation (7.11) that
$l_* := l_\Delta + \lfloor s'/2 \rfloor $
, and observe from equation (7.11) that
![]() $(j_*,l_*) \in \Delta '$
whenever
$(j_*,l_*) \in \Delta '$
whenever
![]() $j_*$
lies in the interval
$j_*$
lies in the interval
and similarly
![]() $(j_*,l_*) \in \Delta ''$
whenever
$(j_*,l_*) \in \Delta ''$
whenever
By Lemma 7.4, these two intervals cannot have any integer point in common; thus
Applying equation (7.66) and the definition of
![]() $l_*$
, we conclude that
$l_*$
, we conclude that
and hence by equation (7.60)
We conclude that for the triangles
![]() $\Delta '$
in
$\Delta '$
in
![]() ${\mathcal T}$
obeying equation (7.66) with
${\mathcal T}$
obeying equation (7.66) with
![]() $s_{\Delta '} \geq s'$
, the points
$s_{\Delta '} \geq s'$
, the points
![]() $(j_{\Delta '}, l_\Delta )$
are
$(j_{\Delta '}, l_\Delta )$
are
![]() $\gg s'$
-separated. Let
$\gg s'$
-separated. Let
![]() $\Sigma $
denote the collection of such points; thus
$\Sigma $
denote the collection of such points; thus
![]() $\Sigma $
is a
$\Sigma $
is a
![]() $\gg s'$
-separated set of points, and outside of the event
$\gg s'$
-separated set of points, and outside of the event
![]() $E'$
,
$E'$
,
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
can only occur in a triangle
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
can only occur in a triangle
![]() $\Delta '$
with
$\Delta '$
with
![]() $s_{\Delta '} \geq s'$
if
$s_{\Delta '} \geq s'$
if
We conclude that
From equation (7.48), we see that
 $$ \begin{align*} &\mathbb{P}\left( (j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} = (j_{\Delta'},l_\Delta) + O( A^2(1+p) ) \right)\\ &\quad\quad\ll \frac{A^2(1+p)}{s^{1/2}} G_{1+s}\left( c \left(j_{\Delta'}-j - \frac{s}{4}\right) \right)\\ &\quad\quad\ll \frac{A^2(1+p)}{s'} \sum_{j' = j_{\Delta'} + O(s')} \frac{1}{s^{1/2}} G_{1+s}\left( c \left(j'-j - \frac{s}{4}\right) \right). \end{align*} $$
$$ \begin{align*} &\mathbb{P}\left( (j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} = (j_{\Delta'},l_\Delta) + O( A^2(1+p) ) \right)\\ &\quad\quad\ll \frac{A^2(1+p)}{s^{1/2}} G_{1+s}\left( c \left(j_{\Delta'}-j - \frac{s}{4}\right) \right)\\ &\quad\quad\ll \frac{A^2(1+p)}{s'} \sum_{j' = j_{\Delta'} + O(s')} \frac{1}{s^{1/2}} G_{1+s}\left( c \left(j'-j - \frac{s}{4}\right) \right). \end{align*} $$
Summing and using the
![]() $\gg s'$
-separated nature of
$\gg s'$
-separated nature of
![]() $\Sigma $
, we conclude that
$\Sigma $
, we conclude that
 $$ \begin{align*} \mathbb{P}\left( {\operatorname{dist}}( (j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}, \Sigma ) \ll A^2(1+p) \right) &\ll \frac{A^2(1+p)}{s'} \sum_{j' \in \mathbb{Z}} \frac{1}{s^{1/2}} G_{1+s}\left( c \left(j'-j - \frac{s}{4}\right) \right) \\ &\ll \frac{A^2(1+p)}{s'} \end{align*} $$
$$ \begin{align*} \mathbb{P}\left( {\operatorname{dist}}( (j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}, \Sigma ) \ll A^2(1+p) \right) &\ll \frac{A^2(1+p)}{s'} \sum_{j' \in \mathbb{Z}} \frac{1}{s^{1/2}} G_{1+s}\left( c \left(j'-j - \frac{s}{4}\right) \right) \\ &\ll \frac{A^2(1+p)}{s'} \end{align*} $$
and the claim in equation (7.62) follows.
From Lemma 7.10, we have
whenever
![]() $0 \leq p \leq m^{0.1}$
. Thus by the union bound, if
$0 \leq p \leq m^{0.1}$
. Thus by the union bound, if
![]() $E_*$
denotes the union of the
$E_*$
denotes the union of the
![]() $E_{p,4^A (1+p)^3}$
for
$E_{p,4^A (1+p)^3}$
for
![]() $0 \leq p \leq m^{0.1}$
, then
$0 \leq p \leq m^{0.1}$
, then
Next, we apply Lemma 7.9 with
![]() $(j',l') := (j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
to conclude that
$(j',l') := (j,l) + \mathbf {v}_{[1,\mathbf {k}]}$
to conclude that
 $$ \begin{align*}\mathbb{E} \exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} + \varepsilon \min(\mathbf{r},R) \right) \leq \exp(\varepsilon),\end{align*} $$
$$ \begin{align*}\mathbb{E} \exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} + \varepsilon \min(\mathbf{r},R) \right) \leq \exp(\varepsilon),\end{align*} $$
where now
![]() $\mathbf {r} = \mathbf {r}((j,l) + \mathbf {v}_{[1,\mathbf {k}]})$
and
$\mathbf {r} = \mathbf {r}((j,l) + \mathbf {v}_{[1,\mathbf {k}]})$
and
![]() $\mathbf {t}_i = \mathbf {t}_i((j,l) + \mathbf {v}_{[1,\mathbf {k}]})$
. If we then let
$\mathbf {t}_i = \mathbf {t}_i((j,l) + \mathbf {v}_{[1,\mathbf {k}]})$
. If we then let
![]() $F_*$
to be the event that
$F_*$
to be the event that
 $$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} + \varepsilon \min(\mathbf{r},R) \right)> 10^{A+2} \exp(\varepsilon)\end{align*} $$
$$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} + \varepsilon \min(\mathbf{r},R) \right)> 10^{A+2} \exp(\varepsilon)\end{align*} $$
then by Markov’s inequality we have
Outside of the event
![]() $F_*$
, we have
$F_*$
, we have
 $$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} + \varepsilon \min(\mathbf{r},R) \right) \ll 10^A\end{align*} $$
$$ \begin{align*}\exp\left( - \sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} + \varepsilon \min(\mathbf{r},R) \right) \ll 10^A\end{align*} $$
which implies that
 $$ \begin{align*}\sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}) \gg \varepsilon \min(\mathbf{r},R) - O( A ).\end{align*} $$
$$ \begin{align*}\sum_{p=1}^{\mathbf{t}_{\min(\mathbf{r},R)}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}) \gg \varepsilon \min(\mathbf{r},R) - O( A ).\end{align*} $$
In particular, if we set
![]() $R := \lfloor A^2 / \varepsilon ^4\rfloor $
, we have
$R := \lfloor A^2 / \varepsilon ^4\rfloor $
, we have
 $$ \begin{align} \sum_{p=1}^{\mathbf{t}_{R}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}) \gg \frac{A^2}{\varepsilon^3} \end{align} $$
$$ \begin{align} \sum_{p=1}^{\mathbf{t}_{R}} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]}) \gg \frac{A^2}{\varepsilon^3} \end{align} $$
whenever we lie outside of
![]() $F_*$
and
$F_*$
and
![]() $\mathbf {r} \geq R$
.
$\mathbf {r} \geq R$
.
Now suppose we lie outside of both
![]() $E_*$
and
$E_*$
and
![]() $F_*$
, so in particular equation (7.67) holds. To prove equation (7.56), it will now suffice to show the deterministic claim
$F_*$
, so in particular equation (7.67) holds. To prove equation (7.56), it will now suffice to show the deterministic claim
 $$ \begin{align} \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} )> \frac{10 A}{\varepsilon^3}. \end{align} $$
$$ \begin{align} \sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} )> \frac{10 A}{\varepsilon^3}. \end{align} $$
We argue by contradiction. Suppose that equation (7.68) fails; thus
 $$ \begin{align*}\sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \leq \frac{10 A}{\varepsilon^3}.\end{align*} $$
$$ \begin{align*}\sum_{p=0}^{P-1} 1_W((j,l) + \mathbf{v}_{[1,\mathbf{k}+p]} ) \leq \frac{10 A}{\varepsilon^3}.\end{align*} $$
Then the point
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
is white for at most
$(j,l) + \mathbf {v}_{[1,\mathbf {k}+p]}$
is white for at most
![]() $10 A/\varepsilon ^3$
values of
$10 A/\varepsilon ^3$
values of
![]() $0 \leq p \leq P-1$
, so in particular for P large enough there is
$0 \leq p \leq P-1$
, so in particular for P large enough there is
![]() $0 \leq p \leq 10A/\varepsilon ^3+1 = O_{A,\varepsilon }(1)$
such that
$0 \leq p \leq 10A/\varepsilon ^3+1 = O_{A,\varepsilon }(1)$
such that
![]() $(j,l) + \mathbf {v} _{[1,\mathbf {k}+p]}$
is black. By Lemma 7.4, this point lies in a triangle
$(j,l) + \mathbf {v} _{[1,\mathbf {k}+p]}$
is black. By Lemma 7.4, this point lies in a triangle
![]() $\Delta ' \in {\mathcal T}$
. As we are outside
$\Delta ' \in {\mathcal T}$
. As we are outside
![]() $E_*$
, the event
$E_*$
, the event
![]() $E_{p,4^A(1+p^3)}$
fails, so we have
$E_{p,4^A(1+p^3)}$
fails, so we have
Thus by equation (7.11), for
![]() $p'$
in the range
$p'$
in the range
we must have
![]() $l + \mathbf {l}_{[1,\mathbf {k}+p']}> l_{\Delta '}$
, hence we exit
$l + \mathbf {l}_{[1,\mathbf {k}+p']}> l_{\Delta '}$
, hence we exit
![]() $\Delta '$
(and increment the random variable
$\Delta '$
(and increment the random variable
![]() $\mathbf {r}$
). In particular, if
$\mathbf {r}$
). In particular, if
then we can find
such that
![]() $l + \mathbf {l}_{[1,\mathbf {k}+p']}> l_{\Delta '}$
and
$l + \mathbf {l}_{[1,\mathbf {k}+p']}> l_{\Delta '}$
and
![]() $(j,l) + \mathbf {v}_{[1,\mathbf {k} +p]}$
is black (and therefore lies in a new triangle
$(j,l) + \mathbf {v}_{[1,\mathbf {k} +p]}$
is black (and therefore lies in a new triangle
![]() $\Delta ''$
). Iterating this R times, we conclude (if P is sufficiently large depending on
$\Delta ''$
). Iterating this R times, we conclude (if P is sufficiently large depending on
![]() $A,\varepsilon $
) that
$A,\varepsilon $
) that
![]() $\mathbf {r} \geq R$
and that
$\mathbf {r} \geq R$
and that
![]() $\mathbf {t}_R \leq P$
. Choosing P large enough so that all the previous arguments are justified, the claim in equation (7.68) now follows from equation (7.67), giving the required contradiction. This (finally!) concludes the proof of equation (7.41), and hence Proposition 7.8. As discussed previously, this implies Propositions 7.3, 7.1, 1.17 and Theorem 1.3.
$\mathbf {t}_R \leq P$
. Choosing P large enough so that all the previous arguments are justified, the claim in equation (7.68) now follows from equation (7.67), giving the required contradiction. This (finally!) concludes the proof of equation (7.41), and hence Proposition 7.8. As discussed previously, this implies Propositions 7.3, 7.1, 1.17 and Theorem 1.3.
Acknowledgments
The author thanks Marek Biskup for useful discussions and Ben Green, Matthias Hippold, Alex Kontorovich, Alexandre Patriota, Sankeerth Rao, Mary Rees, Lior Silberman and several anonymous commenters on his blog for corrections and other comments. We are especially indebted to the anonymous referee for a careful reading and many useful suggestions.
Conflicts of interest
None.
Financial support
The author is supported by NSF grant DMS-1764034 and by a Simons Investigator Award.