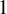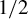1 results
Schmidt games and Cantor winning sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 71-110
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation