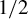1. Introduction and results
When attacking various problems in Diophantine approximation, the application of certain games has proven extremely fruitful. Many authors have appealed to Schmidt’s celebrated game [Reference Schmidt37] (e.g. [Reference Broderick, Bugeaud, Fishman, Kleinbock and Weiss10, Reference Dani, Dodson and Vickers15, Reference Einsiedler and Tseng18, Reference Färm20, Reference Fishman23, Reference Kleinbock and Weiss31, Reference Moshchevitin34, Reference Tseng39]), the absolute game [Reference McMullen33] (e.g. [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11, Reference Chaika, Cheung and Masur14, Reference Fishman, Simmons and Urbański26, Reference Haynes, Koivusalo, Walton and Sadun29, Reference Mayeda and Merrill32]), and the potential game [Reference Fishman, Simmons and Urbański26, Appendix C] (e.g. [Reference An, Ghosh, Guan and Ly3, Reference An, Guan and Kleinbock4, Reference Guan and Yu28, Reference Nesharim and Simmons35, Reference Wu40, Reference Wu41]). It is the amenable properties of the winning sets associated with games of this type that make the games such attractive tools. These properties most commonly include the following (here we use winning in a loose sense to mean winning for either the
![]() $\alpha $
game, the c potential game, or the absolute game).
$\alpha $
game, the c potential game, or the absolute game).
-
(W1) A winning set is dense within the ambient space. In
 $\mathbb {R}^N$
, winning sets are thick; that is, their intersection with any open set has Hausdorff dimension N.
$\mathbb {R}^N$
, winning sets are thick; that is, their intersection with any open set has Hausdorff dimension N. -
(W2) The intersection of a countable collection of winning sets is winning.
-
(W3) The image of a winning set under a certain type of mapping (depending on the game in question) is winning.
At the same time, many related problems in Diophantine approximation have been solved via the method of constructing certain tree-like (or ‘Cantor-type’) structures inside a Diophantine set of interest [Reference An1, Reference An2, Reference Badziahin, Pollington and Velani6–Reference Beresnevich8, Reference Davenport16, Reference Pollington and Velani36, Reference Yang42]. One of the key ingredients in the proof of a famous Schmidt conjecture in [Reference Badziahin, Pollington and Velani6] was the construction of a certain generalized Cantor set in
![]() $\mathbb {R}$
. The main ideas were formalized in a subsequent paper [Reference Badziahin and Velani7] and then in [Reference Badziahin and Harrap5], the theory of generalized Cantor sets and Cantor winning sets was finalized in the general setting of complete metric spaces and a host of further applications to problems in Diophantine approximation was given. The family of
$\mathbb {R}$
. The main ideas were formalized in a subsequent paper [Reference Badziahin and Velani7] and then in [Reference Badziahin and Harrap5], the theory of generalized Cantor sets and Cantor winning sets was finalized in the general setting of complete metric spaces and a host of further applications to problems in Diophantine approximation was given. The family of
![]() $\varepsilon $
Cantor winning sets satisfies properties (W1)–(W3).
$\varepsilon $
Cantor winning sets satisfies properties (W1)–(W3).
It is therefore very natural to investigate how these two different approaches are related, and that is precisely the intention of this paper.
1.1. Known connections
In §2, we provide a complete set of definitions for the unfamiliar reader, along with further commentary relating to the results in this and the succeeding subsection.
The main results of this paper can be summarized in Figure 1. In Figure 1, the solid arrows represent known implications, the dashed arrows represent our new results, and a crossed arrow stands for where an implication does not hold in general.

Figure 1 Main results.
The following connections are already known.
Proposition 1.1. [Reference McMullen33]
If
![]() $E \subseteq \mathbb {R}^N$
is absolute winning, then E is
$E \subseteq \mathbb {R}^N$
is absolute winning, then E is
![]() $\alpha $
winning for every
$\alpha $
winning for every
![]() $\alpha \in (0, 1/2)$
.
$\alpha \in (0, 1/2)$
.
One can actually slightly improve on this via the following folklore argument (see [Reference Guan and Yu28, Proposition 2.1] for a related observation).
Proposition 1.2. Let X be a complete metric space. If
![]() $E\subseteq X$
is winning and
$E\subseteq X$
is winning and
![]() $\alpha _0: = \sup \{\alpha :E \text { is } \alpha \text { winning}\}$
, then E is
$\alpha _0: = \sup \{\alpha :E \text { is } \alpha \text { winning}\}$
, then E is
![]() $\alpha _0$
winning.
$\alpha _0$
winning.
For the sake of completeness, we will prove this proposition in §2. Potential winning is related to absolute winning by the following proposition.
Proposition 1.3. [Reference Fishman, Simmons and Urbański26, Theorem C.8]
Let X be a complete doubling metric space. (See Definition 2.21 for the definition of doubling metric spaces.) If
![]() $E \subseteq X$
is c potential winning for every
$E \subseteq X$
is c potential winning for every
![]() $c>0$
(that is,
$c>0$
(that is,
![]() $0$
potential winning), then E is absolute winning.
$0$
potential winning), then E is absolute winning.
Meanwhile, absolute winning is related to Cantor winning in the following way.
Proposition 1.4. [Reference Badziahin and Harrap5, Theorem 12]
Absolute winning subsets of
![]() $\mathbb {R}^N$
are
$\mathbb {R}^N$
are
![]() $1$
Cantor winning.
$1$
Cantor winning.
1.2. New results
In some sense, the above statements suggest that the construction of Cantor winning sets mimics the playing of a topological game. In §3.1, we introduce a new game called the ‘Cantor game’. We prove that its associated winning sets are exactly the Cantor winning sets (cf. Theorem 3.2); to do this, we use ideas related to the potential game. This serves as a justification for the term ‘Cantor winning’.
Next, we prove a connection between Cantor winning and potential winning, and, in particular, provide a converse to Proposition 1.4.
Theorem 1.5. A set
![]() $E \subseteq \mathbb {R}^N$
is
$E \subseteq \mathbb {R}^N$
is
![]() $\varepsilon $
Cantor winning if and only if it is
$\varepsilon $
Cantor winning if and only if it is
![]() $N(1-\varepsilon )$
potential winning. In particular, E is Cantor winning if and only if E is potential winning, and if
$N(1-\varepsilon )$
potential winning. In particular, E is Cantor winning if and only if E is potential winning, and if
![]() $E\subseteq \mathbb {R}^N$
is
$E\subseteq \mathbb {R}^N$
is
![]() $1$
Cantor winning, then it is absolute winning.
$1$
Cantor winning, then it is absolute winning.
Remark 1.6. It is proved in [Reference Badziahin and Harrap5, Theorem 5.2] that hyperplane absolute winning sets (cf. §2.2 for the definition) in
![]() $\mathbb {R}^N$
are
$\mathbb {R}^N$
are
![]() ${1}/{N}$
Cantor winning; however, the converse is not true. It is possible to develop a theory of generalized Cantor sets in which the removed sets come from neighborhoods of hyperplanes and then use the hyperplane potential game (cf. [Reference Fishman, Simmons and Urbański26, Appendix C] or [Reference Nesharim and Simmons35] for the definition) to state a complete analogue of Theorem 1.5. This will not be pursued in this note.
${1}/{N}$
Cantor winning; however, the converse is not true. It is possible to develop a theory of generalized Cantor sets in which the removed sets come from neighborhoods of hyperplanes and then use the hyperplane potential game (cf. [Reference Fishman, Simmons and Urbański26, Appendix C] or [Reference Nesharim and Simmons35] for the definition) to state a complete analogue of Theorem 1.5. This will not be pursued in this note.
The connection between winning sets for Schmidt’s game and Cantor winning sets is more delicate, as demonstrated by the existence of the following counterexamples (which are given explicitly in §5).
Theorem 1.7. There is a Cantor winning set in
![]() $\mathbb {R}$
that is not winning.
$\mathbb {R}$
that is not winning.
Theorem 1.8. There is a winning set in
![]() $\mathbb {R}$
that is not Cantor winning.
$\mathbb {R}$
that is not Cantor winning.
However, a partial result connecting Cantor winning sets and winning sets when some restrictions are placed on the parameters is possible.
Theorem 1.9. Let
![]() $E\subseteq \mathbb {R}^N$
be an
$E\subseteq \mathbb {R}^N$
be an
![]() $\varepsilon $
Cantor winning set. Then for every
$\varepsilon $
Cantor winning set. Then for every
![]() $c> N(1-\varepsilon )$
, there exists
$c> N(1-\varepsilon )$
, there exists
![]() $\gamma> 0$
such that for all
$\gamma> 0$
such that for all
![]() $\alpha ,\beta> 0$
with
$\alpha ,\beta> 0$
with
![]() $\alpha < \gamma (\alpha \beta )^{c/N}$
, the set E is
$\alpha < \gamma (\alpha \beta )^{c/N}$
, the set E is
![]() $(\alpha ,\beta )$
winning.
$(\alpha ,\beta )$
winning.
Even though Cantor winning does not imply winning, the intersection of the corresponding sets has full Hausdorff dimension.
Theorem 1.10. The intersection in
![]() $\mathbb {R}^N$
of a winning set for Schmidt’s game and a Cantor winning set has Hausdorff dimension N.
$\mathbb {R}^N$
of a winning set for Schmidt’s game and a Cantor winning set has Hausdorff dimension N.
That being said, we prove a surprising result regarding subsets of the real line.
Theorem 1.11. If a set
![]() $E \subseteq \mathbb {R}$
is
$E \subseteq \mathbb {R}$
is
![]() $1/2$
winning, then it is
$1/2$
winning, then it is
![]() $1$
Cantor winning.
$1$
Cantor winning.
In view of Theorem 1.11, Propositions 1.1 and 1.2, and Theorem 1.5, we deduce the following equivalence.
Corollary 1.12. The following statements about a set
![]() $E \subseteq \mathbb {R}$
are equivalent:
$E \subseteq \mathbb {R}$
are equivalent:
-
(1) E is
 $1/2$
winning;
$1/2$
winning; -
(2) E is
 $1$
Cantor winning;
$1$
Cantor winning; -
(3) E is absolute winning.
In [Reference Beresnevich8], the notion of Cantor rich subsets of
![]() $\mathbb {R}$
was introduced. Cantor rich sets were shown to satisfy some of the desirable properties associated with winning sets, and have been applied since elsewhere [Reference Yang42]. As an application of the results in this paper, we can prove that Cantor rich and Cantor winning coincide.
$\mathbb {R}$
was introduced. Cantor rich sets were shown to satisfy some of the desirable properties associated with winning sets, and have been applied since elsewhere [Reference Yang42]. As an application of the results in this paper, we can prove that Cantor rich and Cantor winning coincide.
Theorem 1.13. A set
![]() $E\subseteq \mathbb {R}$
is Cantor rich in an interval
$E\subseteq \mathbb {R}$
is Cantor rich in an interval
![]() $B_0$
if and only if E is Cantor winning in
$B_0$
if and only if E is Cantor winning in
![]() $B_0$
.
$B_0$
.
Another way to measure how large a set is, is to consider its intersections with classes of tamed sets. In fact, proving non-empty intersection with certain classes of sets motivated the invention of the absolute game. For example, it is well known that absolute winning sets are large in the following dual sense [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11].
-
(W4) The intersection of an absolute winning set with any closed non-empty uniformly perfect set is non-empty.
We demonstrate that a similar property holds for Cantor winning sets. In fact, Cantor winning Borel sets are characterized by an analogue of property (W4).
Theorem 1.14. Let
![]() $E\subseteq \mathbb {R}^N$
. If E is
$E\subseteq \mathbb {R}^N$
. If E is
![]() $\varepsilon _0$
Cantor winning, then any
$\varepsilon _0$
Cantor winning, then any
![]() $0\leq \varepsilon <\varepsilon _0$
and
$0\leq \varepsilon <\varepsilon _0$
and
![]() $K \in \mathbb {R}^N$
which is
$K \in \mathbb {R}^N$
which is
![]() $N(1-\varepsilon )$
Ahlfors regular satisfy
$N(1-\varepsilon )$
Ahlfors regular satisfy
![]() $E\cap K\neq \emptyset $
. If E is Borel, then the converse is also true.
$E\cap K\neq \emptyset $
. If E is Borel, then the converse is also true.
Moreover, the intersection of Cantor winning sets with Ahlfors regular sets is often large in terms of Hausdorff dimension (cf. Theorem 4.7). The characterization in Theorem 1.14 makes the notion of Cantor winning sets natural from a geometric point of view.
Remark 1.15. Continuing Remark 1.6, it is also possible to characterize hyperplane absolute winning sets as sets which have a non-trivial intersection with any closed hyperplane diffuse fractal (cf. [Reference Broderick, Bugeaud, Fishman, Kleinbock and Weiss10, Definition 4.2]). This characterization is not discussed in this note.
As a typical example of a Cantor winning set, we suggest the following.
Theorem 1.16. Let
![]() $X=\{0,1\}^{\mathbb {N}}$
with the metric
$X=\{0,1\}^{\mathbb {N}}$
with the metric
![]() $d(x,y) = 2^{-v(x,y)}$
, where
$d(x,y) = 2^{-v(x,y)}$
, where
![]() $v(x,y)$
denotes the length of the longest common initial segment of x and y. Let
$v(x,y)$
denotes the length of the longest common initial segment of x and y. Let
![]() $T:X\to X$
be the left shift map. If
$T:X\to X$
be the left shift map. If
![]() $K\subseteq X$
satisfies
$K\subseteq X$
satisfies
![]() $\dim _H K < 1$
, then the set
$\dim _H K < 1$
, then the set
is
![]() $1 - \dim _H K$
Cantor winning or, equivalently,
$1 - \dim _H K$
Cantor winning or, equivalently,
![]() $\dim _H K$
potential winning.
$\dim _H K$
potential winning.
Here,
![]() $\dim _H$
stands for the Hausdorff dimension. The set E in equation (1) was first considered by Dolgopyat [Reference Dolgopyat17], who proved that
$\dim _H$
stands for the Hausdorff dimension. The set E in equation (1) was first considered by Dolgopyat [Reference Dolgopyat17], who proved that
![]() $\dim _H E=1$
. Unlike the property of having full Hausdorff dimension, the potential winning property passes automatically to subspaces (see Lemma 4.4). Hence, in particular, using the notation of Theorem 1.16, if
$\dim _H E=1$
. Unlike the property of having full Hausdorff dimension, the potential winning property passes automatically to subspaces (see Lemma 4.4). Hence, in particular, using the notation of Theorem 1.16, if
![]() $Y\subseteq X$
is a subshift of finite type and
$Y\subseteq X$
is a subshift of finite type and
![]() $K\subseteq X$
satisfies
$K\subseteq X$
satisfies
![]() $\dim _H (K\cap Y) < \dim _H Y$
, then Theorems 1.16 and 4.7 imply that
$\dim _H (K\cap Y) < \dim _H Y$
, then Theorems 1.16 and 4.7 imply that
![]() $\dim _H (E\cap Y) = \dim _H Y$
, which is exactly the content of [Reference Dolgopyat17, Theorem 1].
$\dim _H (E\cap Y) = \dim _H Y$
, which is exactly the content of [Reference Dolgopyat17, Theorem 1].
The set of all points whose orbit closure misses a given subset is considered in various contexts, such as piecewise expanding maps of the interval and Anosov diffeomorphisms on compact surfaces [Reference Dolgopyat17], certain partially hyperbolic maps [Reference Campos and Gelfert13, Reference Wu41], rational maps on the Riemann sphere [Reference Campos and Gelfert12], and
![]() $\beta $
shifts [Reference Färm and Persson21, Reference Färm, Persson and Schmeling22]. We suggest that Theorem 1.16 might be generalizable to these contexts; however, we choose to present the proof in the above prototypical example. See also [Reference Bilyk, Ma, Pipher and Spencer9] for a related problem where the rate at which the orbit is allowed to approach the subset K depends on the geometrical properties of K.
$\beta $
shifts [Reference Färm and Persson21, Reference Färm, Persson and Schmeling22]. We suggest that Theorem 1.16 might be generalizable to these contexts; however, we choose to present the proof in the above prototypical example. See also [Reference Bilyk, Ma, Pipher and Spencer9] for a related problem where the rate at which the orbit is allowed to approach the subset K depends on the geometrical properties of K.
2. Background, notation, and definitions
We formally define the concepts introduced in §1. Each of the games we describe below is played between two players, Alice and Bob, in a complete metric space
![]() $(X,\mathbf {d})$
. A ball in
$(X,\mathbf {d})$
. A ball in
![]() $B\subseteq X$
is specified by its center and radius, denoted by
$B\subseteq X$
is specified by its center and radius, denoted by
![]() $\mathrm {cent}(B)$
and
$\mathrm {cent}(B)$
and
![]() $\mathrm {rad}(B)$
, respectively.
$\mathrm {rad}(B)$
, respectively.
2.1. Schmidt’s game
Given two real parameters
![]() $\alpha ,\beta \in (0,1)$
, Schmidt’s
$\alpha ,\beta \in (0,1)$
, Schmidt’s
![]() $(\alpha , \beta )$
game begins with Bob choosing an arbitrary closed ball
$(\alpha , \beta )$
game begins with Bob choosing an arbitrary closed ball
![]() $B_0\subseteq X$
. Alice and Bob then take turns to choose a sequence of nested closed balls (Alice chooses balls
$B_0\subseteq X$
. Alice and Bob then take turns to choose a sequence of nested closed balls (Alice chooses balls
![]() $A_i$
and Bob chooses balls
$A_i$
and Bob chooses balls
![]() $B_i$
) satisfying both
$B_i$
) satisfying both
and
Since the radii of the balls tend to zero, at the end of the game, the intersection of Bob’s (or Alice’s) balls must consist of a single point. See Figure 2 for a pictorial representation of the game, in which the shaded area represents where Alice has specified Bob must play his next ball. A set
![]() $E\subseteq X$
is called
$E\subseteq X$
is called
![]() $(\alpha ,\beta )$
winning if Alice has a strategy for placing her balls that ensures
$(\alpha ,\beta )$
winning if Alice has a strategy for placing her balls that ensures
 $$ \begin{align} \bigcap_{i =0}^\infty \, B_i \subseteq E. \end{align} $$
$$ \begin{align} \bigcap_{i =0}^\infty \, B_i \subseteq E. \end{align} $$
In this case, we say that Alice wins. The
![]() $\alpha $
game is defined by allowing Bob to choose the parameter
$\alpha $
game is defined by allowing Bob to choose the parameter
![]() $\beta $
and then continuing as in the
$\beta $
and then continuing as in the
![]() $(\alpha ,\beta )$
game. We say that
$(\alpha ,\beta )$
game. We say that
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $\alpha $
winning if Alice has a winning strategy for the
$\alpha $
winning if Alice has a winning strategy for the
![]() $\alpha $
game. Note that
$\alpha $
game. Note that
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $\alpha $
winning if and only if E is
$\alpha $
winning if and only if E is
![]() $(\alpha ,\beta )$
winning for all
$(\alpha ,\beta )$
winning for all
![]() $0<\beta <1$
. Finally, Schmidt’s game is defined by allowing Alice to choose
$0<\beta <1$
. Finally, Schmidt’s game is defined by allowing Alice to choose
![]() $0<\alpha <1$
and then continuing as in the
$0<\alpha <1$
and then continuing as in the
![]() $\alpha $
game. We say
$\alpha $
game. We say
![]() $E\subseteq X$
is winning if Alice has a winning strategy for Schmidt’s game. Note that E is winning if and only if it is
$E\subseteq X$
is winning if Alice has a winning strategy for Schmidt’s game. Note that E is winning if and only if it is
![]() $\alpha $
winning for some
$\alpha $
winning for some
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.

Figure 2 Schmidt’s game.
It is easily observed that if a set E is
![]() $\alpha $
winning for some
$\alpha $
winning for some
![]() $\alpha \in (0,1)$
, then E is
$\alpha \in (0,1)$
, then E is
![]() $\alpha '$
winning for every
$\alpha '$
winning for every
![]() $\alpha ' \in (0, \alpha )$
, and that E is
$\alpha ' \in (0, \alpha )$
, and that E is
![]() $\alpha $
winning for some
$\alpha $
winning for some
![]() $\alpha \in (1/2,1)$
if and only if
$\alpha \in (1/2,1)$
if and only if
![]() $E=X$
(cf. [Reference Schmidt37], Lemmas 5 and 8, respectively); that is, the property of being
$E=X$
(cf. [Reference Schmidt37], Lemmas 5 and 8, respectively); that is, the property of being
![]() $1/2$
winning is the strongest possible for a non-trivial subset.
$1/2$
winning is the strongest possible for a non-trivial subset.
Remark 2.1. Strictly speaking, since a ball in an abstract metric space X may not necessarily possess a unique center and radius, Alice and Bob should pick successive pairs of centers and radii for their balls, satisfying certain distance inequalities that formally guarantee that the appropriate subset relations hold between the corresponding balls. However, we will assume that this nuance is accounted for in each player’s strategy.
We end the introduction of Schmidt games with the proof of the folklore Proposition 1.2.
Proof of Proposition 1.2
Fix
![]() $0 < \beta _0 < 1$
, let
$0 < \beta _0 < 1$
, let
![]() $\alpha _0$
be as in the statement. The case
$\alpha _0$
be as in the statement. The case
![]() $\alpha _0=1$
is clear. For
$\alpha _0=1$
is clear. For
![]() $\alpha _0<1$
, set
$\alpha _0<1$
, set
 $$ \begin{align} \alpha = \alpha_0\frac{1 - (\alpha_0 \beta_0)^2 - \beta_0 (1-\alpha_0)}{1 - (\alpha_0 \beta_0)^2 - \alpha_0 \beta_0 (1-\alpha_0)} < \alpha_0,\quad \alpha\beta = (\alpha_0\beta_0)^2. \end{align} $$
$$ \begin{align} \alpha = \alpha_0\frac{1 - (\alpha_0 \beta_0)^2 - \beta_0 (1-\alpha_0)}{1 - (\alpha_0 \beta_0)^2 - \alpha_0 \beta_0 (1-\alpha_0)} < \alpha_0,\quad \alpha\beta = (\alpha_0\beta_0)^2. \end{align} $$
We describe the winning strategy for Alice for the
![]() $(\alpha _0,\beta _0)$
game (Game I) based on her strategy for the
$(\alpha _0,\beta _0)$
game (Game I) based on her strategy for the
![]() $(\alpha ,\beta )$
game (Game II). It can be given as follows.
$(\alpha ,\beta )$
game (Game II). It can be given as follows.
-
(1) Whenever Bob plays a move
 $B_{2n} = B(b_{2n},\rho _{2n})$
in Game I, he correspondingly plays the move
$B_{2n} = B(b_{2n},\rho _{2n})$
in Game I, he correspondingly plays the move
 $B_n' = B(b_n',\rho _n')$
in Game II, where
$B_n' = B(b_n',\rho _n')$
in Game II, where  $$ \begin{align*} (1-\alpha)\rho_n' = (1-\alpha_0) \rho_{2n},\quad b_n' = b_{2n}. \end{align*} $$
$$ \begin{align*} (1-\alpha)\rho_n' = (1-\alpha_0) \rho_{2n},\quad b_n' = b_{2n}. \end{align*} $$
-
(2) When Alice responds to this by playing a move
 $A_{n+1}' = B(a_{n+1}',\alpha \rho _n')$
in Game II (according to her winning strategy), she correspondingly plays the move
$A_{n+1}' = B(a_{n+1}',\alpha \rho _n')$
in Game II (according to her winning strategy), she correspondingly plays the move
 $A_{2n+1} = B(a_{2n+1},\alpha _0 \rho _{2n})$
in Game I, where
$A_{2n+1} = B(a_{2n+1},\alpha _0 \rho _{2n})$
in Game I, where  $$ \begin{align*} a_{2n+1} = a_{n+1}'. \end{align*} $$
$$ \begin{align*} a_{2n+1} = a_{n+1}'. \end{align*} $$
-
(3) When Bob responds to this by playing a move
 $B_{2n+1} = B(b_{2n+1},\rho _{2n+1})$
in Game I, Alice responds by playing the move
$B_{2n+1} = B(b_{2n+1},\rho _{2n+1})$
in Game I, Alice responds by playing the move
 $A_{2n+2} = B(a_{2n+2},\alpha _0 \rho _{2n+1})$
in Game I, where This sets the stage for the next iteration.
$A_{2n+2} = B(a_{2n+2},\alpha _0 \rho _{2n+1})$
in Game I, where This sets the stage for the next iteration. $$ \begin{align*} a_{2n+2} = b_{2n+1}. \end{align*} $$
$$ \begin{align*} a_{2n+2} = b_{2n+1}. \end{align*} $$
To finish the proof, it suffices to check that all of these moves are legal. When
![]() $n=0$
, move 1 is legal because any ball can be Bob’s first move. Move 2 is legal because
$n=0$
, move 1 is legal because any ball can be Bob’s first move. Move 2 is legal because
and move 3 is legal because
![]() $\mathbf {d}(b_{2n+1},a_{2n+2}) = 0$
. When
$\mathbf {d}(b_{2n+1},a_{2n+2}) = 0$
. When
![]() $n\geq 1$
, move 1 is legal because
$n\geq 1$
, move 1 is legal because
 $$ \begin{align*} \mathbf{d}(a_n',b_n') &= \mathbf{d}(a_{2n-1},b_{2n}) \leq \mathbf{d}(a_{2n-1},b_{2n-1}) + \mathbf{d}(a_{2n},b_{2n})\\ &\leq (1-\beta_0)\alpha_0 \rho_{2n-2} + (1-\beta_0)\alpha_0(\alpha_0\beta_0) \rho_{2n-2} = (1-\beta)\alpha\rho_{n-1}'.\\[-37.3pt] \end{align*} $$
$$ \begin{align*} \mathbf{d}(a_n',b_n') &= \mathbf{d}(a_{2n-1},b_{2n}) \leq \mathbf{d}(a_{2n-1},b_{2n-1}) + \mathbf{d}(a_{2n},b_{2n})\\ &\leq (1-\beta_0)\alpha_0 \rho_{2n-2} + (1-\beta_0)\alpha_0(\alpha_0\beta_0) \rho_{2n-2} = (1-\beta)\alpha\rho_{n-1}'.\\[-37.3pt] \end{align*} $$
For details and other properties of winning sets, see Schmidt’s book [Reference Schmidt38].
2.2. The absolute game
The absolute game was introduced by McMullen in [Reference McMullen33]. It is played similarly to Schmidt’s game but instead of choosing a region where Bob must play, Alice now chooses a region where Bob must not play. To be precise, given
![]() $0<\beta <1$
, the
$0<\beta <1$
, the
![]() $\beta $
absolute game is played as follows: Bob first picks some initial ball
$\beta $
absolute game is played as follows: Bob first picks some initial ball
![]() $B_0 \subseteq X$
. Alice and Bob then take turns to place successive closed balls in such a way that
$B_0 \subseteq X$
. Alice and Bob then take turns to place successive closed balls in such a way that
subject to the conditions
See Figure 3 for a pictorial view of the game in
![]() $\mathbb R^2$
.
$\mathbb R^2$
.

Figure 3 The absolute game.
If
![]() $r_i:= \mathrm {rad}(B_i) \not \rightarrow 0$
, then we say that Alice wins by default. We say a set
$r_i:= \mathrm {rad}(B_i) \not \rightarrow 0$
, then we say that Alice wins by default. We say a set
![]() $E \subseteq X$
is
$E \subseteq X$
is
![]() $\beta $
absolute winning if Alice has a strategy which guarantees that either she wins by default or equation (3) is satisfied. In this case, we say that Alice wins. The absolute game is defined by allowing Bob to choose
$\beta $
absolute winning if Alice has a strategy which guarantees that either she wins by default or equation (3) is satisfied. In this case, we say that Alice wins. The absolute game is defined by allowing Bob to choose
![]() $0<\beta <1$
on his first turn and then continuing as in the
$0<\beta <1$
on his first turn and then continuing as in the
![]() $\beta $
absolute game. A set is called absolute winning if Alice has a winning strategy for the absolute game. Note that a set is absolute winning if and only if it is
$\beta $
absolute game. A set is called absolute winning if Alice has a winning strategy for the absolute game. Note that a set is absolute winning if and only if it is
![]() $\beta $
absolute winning for every
$\beta $
absolute winning for every
![]() $0<\beta <1$
.
$0<\beta <1$
.
A useful generalization of the absolute game was introduced in [Reference Fishman, Simmons and Urbański26, Appendix C]. Let
![]() $\mathcal {H}$
be any collection of non-empty closed subsets of X. The
$\mathcal {H}$
be any collection of non-empty closed subsets of X. The
![]() $\mathcal {H}$
absolute game is defined in a similar way to the absolute game, but Alice is now allowed to choose a neighborhood of an element
$\mathcal {H}$
absolute game is defined in a similar way to the absolute game, but Alice is now allowed to choose a neighborhood of an element
![]() $H\in \mathcal {H}$
, namely,
$H\in \mathcal {H}$
, namely,
McMullen’s absolute game is the same as the
![]() $\mathcal {H}$
absolute game when
$\mathcal {H}$
absolute game when
![]() $\mathcal {H}$
is the collection of all singletons. The first generalization of the absolute game was the k-dimensional absolute game, which is the
$\mathcal {H}$
is the collection of all singletons. The first generalization of the absolute game was the k-dimensional absolute game, which is the
![]() $\mathcal {H}$
absolute game where
$\mathcal {H}$
absolute game where
![]() $X=\mathbb {R}^N$
and
$X=\mathbb {R}^N$
and
![]() $\mathcal {H}$
is the collection of k-dimensional hyperplanes in
$\mathcal {H}$
is the collection of k-dimensional hyperplanes in
![]() $\mathbb {R}^N$
. When
$\mathbb {R}^N$
. When
![]() $k=N-1$
, the associated winning sets are often referred to by the acronym HAW, short for ‘hyperplane absolute winning’ [Reference Broderick, Bugeaud, Fishman, Kleinbock and Weiss10]. Some of the results in this note regarding the absolute game may be generalized to the context of
$k=N-1$
, the associated winning sets are often referred to by the acronym HAW, short for ‘hyperplane absolute winning’ [Reference Broderick, Bugeaud, Fishman, Kleinbock and Weiss10]. Some of the results in this note regarding the absolute game may be generalized to the context of
![]() $\mathcal {H}$
absolute game but we will not pursue this line further in the current note.
$\mathcal {H}$
absolute game but we will not pursue this line further in the current note.
Remark 2.2. These definitions deserve some justification. We do not require
![]() $0 < \beta < \tfrac 13$
as in the original definitions for
$0 < \beta < \tfrac 13$
as in the original definitions for
![]() $X=\mathbb {R}^N$
[Reference Broderick, Bugeaud, Fishman, Kleinbock and Weiss10, Reference McMullen33]. To cover those cases where Bob chooses
$X=\mathbb {R}^N$
[Reference Broderick, Bugeaud, Fishman, Kleinbock and Weiss10, Reference McMullen33]. To cover those cases where Bob chooses
![]() $\tfrac 13\leq \beta < 1$
, in which Bob might not have a legal move that satisfies equation (5) on one of his turns, we declare that Bob is losing if this happens. This gives the wanted effect when
$\tfrac 13\leq \beta < 1$
, in which Bob might not have a legal move that satisfies equation (5) on one of his turns, we declare that Bob is losing if this happens. This gives the wanted effect when
![]() $X=\mathbb {R}^N$
, but puts us in a situation that a subset of an abstract metric space might be winning because the space X is not large enough to allow Bob not to lose by default. In this situation, even the empty set might be absolute winning (cf. Remark 4.9). This situation, however, cannot occur when X is uniformly perfect (cf. §2.7).
$X=\mathbb {R}^N$
, but puts us in a situation that a subset of an abstract metric space might be winning because the space X is not large enough to allow Bob not to lose by default. In this situation, even the empty set might be absolute winning (cf. Remark 4.9). This situation, however, cannot occur when X is uniformly perfect (cf. §2.7).
Also note that it is shown in [Reference Fishman, Simmons and Urbański26, Proposition 4.5] that replacing the inequalities in equation (6) with equalities does not change the class of absolute winning sets. The reason for introducing these inequalities is to allow an easy proof of the invariance of absolute winning sets under ‘quasisymmetric maps’ (cf. [Reference McMullen33, Theorem 2.2]).
2.3. The potential game
Given two parameters
![]() $c, \beta>0$
, the
$c, \beta>0$
, the
![]() $(c,\beta )$
potential game begins with Bob picking some initial ball
$(c,\beta )$
potential game begins with Bob picking some initial ball
![]() $B_0 \subseteq X$
. On her
$B_0 \subseteq X$
. On her
![]() $(i+1)$
st turn, Alice chooses a countable collection of closed balls
$(i+1)$
st turn, Alice chooses a countable collection of closed balls
![]() $A_{i+1, k}$
, satisfying
$A_{i+1, k}$
, satisfying
By convention, we assume that a ball always has a positive radius; that is, Alice cannot choose
![]() $A_{i,k}$
to be singletons. Then, Bob on his
$A_{i,k}$
to be singletons. Then, Bob on his
![]() $(i+1)$
st turn chooses a ball
$(i+1)$
st turn chooses a ball
![]() $B_{i+1}\subseteq B_i$
satisfying
$B_{i+1}\subseteq B_i$
satisfying
![]() $\mathrm {rad}(B_{i+1}) \geq \beta \cdot \mathrm {rad}(B_i)$
. See Figure 4 for a demonstration of the playing of such a game in
$\mathrm {rad}(B_{i+1}) \geq \beta \cdot \mathrm {rad}(B_i)$
. See Figure 4 for a demonstration of the playing of such a game in
![]() $\mathbb R^2$
(in which, for simplicity, Bob’s balls do not intersect Alice’s preceding collections—however, it should be understood that this is not a necessary condition for Bob).
$\mathbb R^2$
(in which, for simplicity, Bob’s balls do not intersect Alice’s preceding collections—however, it should be understood that this is not a necessary condition for Bob).

Figure 4 The potential game.
If
or if
![]() $\mathrm {rad}(B_i) \not \rightarrow 0$
, we say that Alice wins by default.
$\mathrm {rad}(B_i) \not \rightarrow 0$
, we say that Alice wins by default.
A set
![]() $E \subseteq X$
is said to be
$E \subseteq X$
is said to be
![]() $(c, \beta )$
potential winning if Alice has a strategy guaranteeing that either she wins by default or equation (3) holds. The
$(c, \beta )$
potential winning if Alice has a strategy guaranteeing that either she wins by default or equation (3) holds. The
![]() $c_0$
potential game is defined by allowing Bob to choose in his first turn the parameters
$c_0$
potential game is defined by allowing Bob to choose in his first turn the parameters
![]() $c>c_0$
and
$c>c_0$
and
![]() $\beta>0$
, and then continue as in the
$\beta>0$
, and then continue as in the
![]() $(c,\beta )$
potential game. A set E is
$(c,\beta )$
potential game. A set E is
![]() $c_0$
potential winning if Alice has a winning strategy for E in the
$c_0$
potential winning if Alice has a winning strategy for E in the
![]() $c_0$
potential game. Note that E is
$c_0$
potential game. Note that E is
![]() $c_0$
potential winning if and only if E is
$c_0$
potential winning if and only if E is
![]() $(c, \beta )$
potential winning for every
$(c, \beta )$
potential winning for every
![]() $c> c_0$
and
$c> c_0$
and
![]() $\beta> 0$
. If X is Ahlfors
$\beta> 0$
. If X is Ahlfors
![]() $\delta $
regular for some
$\delta $
regular for some
![]() $\delta>0$
, the potential game is defined by allowing Alice to choose
$\delta>0$
, the potential game is defined by allowing Alice to choose
![]() $c_0<\delta $
and then continuing as in the
$c_0<\delta $
and then continuing as in the
![]() $c_0$
potential game, and a set E is called potential winning if Alice has a winning strategy in the potential game. Note that E is potential winning if and only if it is
$c_0$
potential game, and a set E is called potential winning if Alice has a winning strategy in the potential game. Note that E is potential winning if and only if it is
![]() $c_0$
potential winning for some
$c_0$
potential winning for some
![]() $c_0<\delta $
.
$c_0<\delta $
.
Remark 2.3. The
![]() $c_0$
potential game with
$c_0$
potential game with
![]() $c_0=0$
was introduced in [Reference Fishman, Simmons and Urbański26, Appendix C] as the potential game. In light of the connections between Cantor, absolute, and potential winning in §3.2 and the geometrical interpretation in §4, it is natural to adjust the definition that appears there to the one that appears here.
$c_0=0$
was introduced in [Reference Fishman, Simmons and Urbański26, Appendix C] as the potential game. In light of the connections between Cantor, absolute, and potential winning in §3.2 and the geometrical interpretation in §4, it is natural to adjust the definition that appears there to the one that appears here.
For the sake of completeness, we will verify properties (W1) and (W2) for potential winning sets. Property (W1) is verified for a class of Ahlfors regular spaces X in Theorem 4.7.
Proposition 2.4. Let
![]() $E_1,E_2\subseteq X$
be
$E_1,E_2\subseteq X$
be
![]() $c_1$
and
$c_1$
and
![]() $c_2$
potential winning, respectively. Then
$c_2$
potential winning, respectively. Then
![]() $E_1\cap E_2$
is
$E_1\cap E_2$
is
![]() $\max \{c_1,c_2\}$
potential winning.
$\max \{c_1,c_2\}$
potential winning.
Proof. Fix arbitrary
![]() $c>\max \{c_1,c_2\}$
and
$c>\max \{c_1,c_2\}$
and
![]() $\beta>0$
. By assumption,
$\beta>0$
. By assumption,
![]() $E_1$
and
$E_1$
and
![]() $E_2$
are both
$E_2$
are both
![]() $(c, \beta ^2)$
potential winning. Now Alice uses the following strategy to win the
$(c, \beta ^2)$
potential winning. Now Alice uses the following strategy to win the
![]() $(c,\beta )$
game on the set
$(c,\beta )$
game on the set
![]() $E_1\cap E_2$
. After Bob’s initial move
$E_1\cap E_2$
. After Bob’s initial move
![]() $B_0$
, Alice chooses the collection
$B_0$
, Alice chooses the collection
![]() $A_{1,k}$
from her
$A_{1,k}$
from her
![]() $(c,\beta ^2)$
winning strategy for the set
$(c,\beta ^2)$
winning strategy for the set
![]() $E_1$
. After Bob’s first move
$E_1$
. After Bob’s first move
![]() $B_1$
, Alice chooses the collection
$B_1$
, Alice chooses the collection
![]() $A^*_{1,k}$
from her
$A^*_{1,k}$
from her
![]() $(c,\beta ^2)$
winning strategy for the set
$(c,\beta ^2)$
winning strategy for the set
![]() $E_2$
, assuming that Bob’s initial move was
$E_2$
, assuming that Bob’s initial move was
![]() $B_1$
.
$B_1$
.
In general, after
![]() $B_{2m}$
, Alice chooses the collection
$B_{2m}$
, Alice chooses the collection
![]() $A_{m,k}$
following her
$A_{m,k}$
following her
![]() $(c,\beta ^2)$
winning strategy for the set
$(c,\beta ^2)$
winning strategy for the set
![]() $E_1$
; after
$E_1$
; after
![]() $B_{2m+1}$
, she chooses the collection
$B_{2m+1}$
, she chooses the collection
![]() $A^*_{m,k}$
following her
$A^*_{m,k}$
following her
![]() $(c,\beta ^2)$
winning strategy for the set
$(c,\beta ^2)$
winning strategy for the set
![]() $E_2$
.
$E_2$
.
It is easy to check that Alice’s moves are legal, because
The same inequality is true for the collections
![]() $A^*_{i+1,k}$
. Also, by construction, either Alice wins by default or
$A^*_{i+1,k}$
. Also, by construction, either Alice wins by default or
![]() $\bigcap _i B_i \subseteq E_1\cap E_2$
.
$\bigcap _i B_i \subseteq E_1\cap E_2$
.
2.4. The strong and the weak Schmidt games
One can define further variants of Schmidt’s original game. The strong game (introduced by McMullen in [Reference McMullen33]) coincides with Schmidt’s game except that the equalities in equation (2) are replaced by the inequalities
Similarly, we define the weak game so that Alice can choose her radii with an inequality but Bob must use equality. Obviously, every weak winning set is winning but the converse is not necessarily true (however, the weak game does not have the intersection property—see later).
One could also define a very strong game, where Alice must use equality but Bob may use inequality.
Remark 2.5. It can be shown that a set is strong winning if and only if it is very strong winning, but this fact will not be needed and hence we skip its proof.
Later in the paper, we will need the following proposition which relates the very strong winning property of a set E and the weak winning property of its complement
![]() $X\setminus E$
.
$X\setminus E$
.
Proposition 2.6. Let
![]() $E\subseteq X$
satisfy the following property: for any
$E\subseteq X$
satisfy the following property: for any
![]() $\beta \in (0,1)$
, there exists
$\beta \in (0,1)$
, there exists
![]() $\alpha>0$
such that E is
$\alpha>0$
such that E is
![]() $(\alpha ,\beta )$
very strong winning. Then
$(\alpha ,\beta )$
very strong winning. Then
![]() $X\setminus E$
is not weak winning.
$X\setminus E$
is not weak winning.
Proof. We need to show that for any
![]() $\beta>0$
, the set
$\beta>0$
, the set
![]() $X\setminus E$
is not
$X\setminus E$
is not
![]() $\beta $
weak winning. To do that, we will provide a winning strategy for Bob that ensures that
$\beta $
weak winning. To do that, we will provide a winning strategy for Bob that ensures that
![]() $\bigcap _{i=0}^\infty B_i \subseteq E$
. On his first turn, Bob chooses
$\bigcap _{i=0}^\infty B_i \subseteq E$
. On his first turn, Bob chooses
![]() $\alpha>0$
such that E is
$\alpha>0$
such that E is
![]() $(\alpha , \beta )$
very strong winning, so that he is now playing the
$(\alpha , \beta )$
very strong winning, so that he is now playing the
![]() $(\beta ,\alpha )$
weak game and chooses an arbitrary ball
$(\beta ,\alpha )$
weak game and chooses an arbitrary ball
![]() $B_0$
. In his subsequent moves, Bob follows Alice’s winning strategy for the
$B_0$
. In his subsequent moves, Bob follows Alice’s winning strategy for the
![]() $(\alpha , \beta )$
very strong game.
$(\alpha , \beta )$
very strong game.
2.5. Cantor winning
For the sake of clarity, we introduce a specialization of the framework presented in [Reference Badziahin and Harrap5], tailored to suit our needs. We first define the notion of a ‘splitting structure’ on X. This is in some sense the minimal amount of structure the metric space needs to allow the construction of generalized Cantor sets (cf. [Reference Badziahin and Harrap5]). Denote by
![]() $\mathcal {B}(X)$
the set of all closed balls. We assume that by definition, to specify a closed ball, it is necessary to specify its center and radius. Note that this means that in some cases, two distinct balls may be set-theoretically equal in the sense of containing the same points (see also Remark 2.1) in X and by
$\mathcal {B}(X)$
the set of all closed balls. We assume that by definition, to specify a closed ball, it is necessary to specify its center and radius. Note that this means that in some cases, two distinct balls may be set-theoretically equal in the sense of containing the same points (see also Remark 2.1) in X and by
![]() $\mathcal {P}(\mathcal {B}(X))$
the set of all subsets of
$\mathcal {P}(\mathcal {B}(X))$
the set of all subsets of
![]() $\mathcal {B}(X)$
. A splitting structure is a quadruple
$\mathcal {B}(X)$
. A splitting structure is a quadruple
![]() $(X,\mathcal {S}, U,f)$
, where:
$(X,\mathcal {S}, U,f)$
, where:
-
•
 $U\subseteq \mathbb {N}$
is an infinite multiplicatively closed set such that if
$U\subseteq \mathbb {N}$
is an infinite multiplicatively closed set such that if
 $u,v\in U$
and
$u,v\in U$
and
 $u\mid v$
, then
$u\mid v$
, then
 $v/u\in U$
;
$v/u\in U$
; -
•
 $f: U\to \mathbb {N}$
is a totally multiplicative function;
$f: U\to \mathbb {N}$
is a totally multiplicative function; -
•
 $\mathcal {S}\;:\mathcal {B}(X)\times U \to \mathcal P(\mathcal {B}(X))$
is a map defined in such a way that for every ball
$\mathcal {S}\;:\mathcal {B}(X)\times U \to \mathcal P(\mathcal {B}(X))$
is a map defined in such a way that for every ball
 $B\in \mathcal {B}(X)$
and
$B\in \mathcal {B}(X)$
and
 $u\in U$
, the set
$u\in U$
, the set
 $\mathcal {S}(B,u)$
consists solely of balls
$\mathcal {S}(B,u)$
consists solely of balls
 $S\subseteq B$
of radius
$S\subseteq B$
of radius
 $\mathrm {rad}(B)/u$
.
$\mathrm {rad}(B)/u$
.
Additionally, we require all these objects to be linked by the following properties:
-
(S1)
 $\#\mathcal {S}(B,u) = f(u)$
(in fact, one can make the definition of a splitting structure slightly more general by removing the function f out of it and replacing condition (S1) with
$\#\mathcal {S}(B,u) = f(u)$
(in fact, one can make the definition of a splitting structure slightly more general by removing the function f out of it and replacing condition (S1) with-
(S1’)
 $\#\mathcal {S}(B,u)$
is finite.
$\#\mathcal {S}(B,u)$
is finite.
In other words, one can let
 $\#\mathcal {S}(B,u)$
vary with respect to B. In this case, instead of the function
$\#\mathcal {S}(B,u)$
vary with respect to B. In this case, instead of the function
 $f(u)$
, we define
$f(u)$
, we define
 $f(B,u):=\#\mathcal {S}(B,u)$
. An enthusiastic reader can verify that in this more general setting, all the results of this paper are still satisfied after minor straightforward adjustments have been made. However, for convenience, we stick with the notation from [Reference Badziahin and Harrap5]);
$f(B,u):=\#\mathcal {S}(B,u)$
. An enthusiastic reader can verify that in this more general setting, all the results of this paper are still satisfied after minor straightforward adjustments have been made. However, for convenience, we stick with the notation from [Reference Badziahin and Harrap5]); -
-
(S2) if
 $S_1,S_2\in \mathcal {S}(B,u)$
and
$S_1,S_2\in \mathcal {S}(B,u)$
and
 $S_1\neq S_2$
, then
$S_1\neq S_2$
, then
 $S_1$
and
$S_1$
and
 $S_2$
may only intersect on the boundary, that is, the distance between their centers must be at least
$S_2$
may only intersect on the boundary, that is, the distance between their centers must be at least
 $\mathrm {rad}(S_1) + \mathrm {rad}(S_2) = 2\mathrm {rad}(B)/u$
;
$\mathrm {rad}(S_1) + \mathrm {rad}(S_2) = 2\mathrm {rad}(B)/u$
; -
(S3) for all
 $u,v\in U$
,
$u,v\in U$
,  $$ \begin{align*} \mathcal{S}(B,uv) = \bigcup_{S \,\in \,\mathcal{S}(B,u)} \mathcal{S}(S,v). \end{align*} $$
$$ \begin{align*} \mathcal{S}(B,uv) = \bigcup_{S \,\in \,\mathcal{S}(B,u)} \mathcal{S}(S,v). \end{align*} $$
Broadly speaking, the set U determines the set of possible ratios of radii of balls in the successive levels of the upcoming Cantor set construction. For any fixed
![]() $B \in \mathcal {B}(X)$
, the function f tells us how many balls inside B of a fixed radius we may choose as candidates for the next level in the Cantor set construction, and the sets
$B \in \mathcal {B}(X)$
, the function f tells us how many balls inside B of a fixed radius we may choose as candidates for the next level in the Cantor set construction, and the sets
![]() $\mathcal {S}(B, u)$
describe the position of these candidate balls.
$\mathcal {S}(B, u)$
describe the position of these candidate balls.
If
![]() $f \equiv 1$
, we say the splitting structure
$f \equiv 1$
, we say the splitting structure
![]() $(X,\mathcal {S}, U,f)$
is trivial. Otherwise, fix a sequence
$(X,\mathcal {S}, U,f)$
is trivial. Otherwise, fix a sequence
![]() $(u_i)_{i\in \mathbb {N}}$
with
$(u_i)_{i\in \mathbb {N}}$
with
![]() $u_i\in U$
such that
$u_i\in U$
such that
![]() $u_i\mid u_{i+1}$
and
$u_i\mid u_{i+1}$
and
![]() $u_i\underset {i\to \infty }{\longrightarrow } \infty $
. Then, one can show [Reference Badziahin and Harrap5, Theorem 2.1] that for any
$u_i\underset {i\to \infty }{\longrightarrow } \infty $
. Then, one can show [Reference Badziahin and Harrap5, Theorem 2.1] that for any
![]() $B_0 \in \mathcal {B}(X)$
, the limit set
$B_0 \in \mathcal {B}(X)$
, the limit set
 $$ \begin{align*} A_\infty(B_0):= \bigcap_{i=1}^\infty \: \bigcup_{B\, \in\, \mathcal{S}(B,u_i)} B \end{align*} $$
$$ \begin{align*} A_\infty(B_0):= \bigcap_{i=1}^\infty \: \bigcup_{B\, \in\, \mathcal{S}(B,u_i)} B \end{align*} $$
is compact and independent of the choice of sequence
![]() $(u_i)_{i\in \mathbb {N}}$
.
$(u_i)_{i\in \mathbb {N}}$
.
Example 2.7. The standard splitting structure on
![]() $X=\mathbb {R}^N$
is with the metric that comes from the sup norm:
$X=\mathbb {R}^N$
is with the metric that comes from the sup norm:
![]() $\mathbf {d}(x,y):=\|x-y\|_\infty $
. The collection of splittings
$\mathbf {d}(x,y):=\|x-y\|_\infty $
. The collection of splittings
![]() $\mathcal {S}(B,u)$
of any closed ball B according to the integer
$\mathcal {S}(B,u)$
of any closed ball B according to the integer
![]() $u\in U = \mathbb {N}$
, into
$u\in U = \mathbb {N}$
, into
![]() $f(u)=u^N$
parts, is defined as follows: cut B into
$f(u)=u^N$
parts, is defined as follows: cut B into
![]() $u^N$
equal square boxes whose edges have length u times less than the edges length of B. One can check that
$u^N$
equal square boxes whose edges have length u times less than the edges length of B. One can check that
![]() $(\mathbb {R}^N,\mathcal {S}, \mathbb {N}, f)$
satisfies properties (S1)–(S3) and is the unique splitting structure for
$(\mathbb {R}^N,\mathcal {S}, \mathbb {N}, f)$
satisfies properties (S1)–(S3) and is the unique splitting structure for
![]() $(\mathbb {R}^N, \mathbf {d})$
with
$(\mathbb {R}^N, \mathbf {d})$
with
![]() $U=\mathbb {N}$
such that
$U=\mathbb {N}$
such that
![]() $A_\infty (B) = B$
for every
$A_\infty (B) = B$
for every
![]() $B\in \mathcal {B}(X)$
.
$B\in \mathcal {B}(X)$
.
In a similar manner, the standard splitting structure on
![]() $\{0,1\}^{\mathbb {N}}$
is with the standard metric
$\{0,1\}^{\mathbb {N}}$
is with the standard metric
![]() $\mathbf {d}(x,y):=2^{-\min \{i\geq 0: x_i\neq y_i\}}$
,
$\mathbf {d}(x,y):=2^{-\min \{i\geq 0: x_i\neq y_i\}}$
,
![]() $U=\{2^i: i\geq 0\}$
,
$U=\{2^i: i\geq 0\}$
,
![]() $f(u)=u$
, and
$f(u)=u$
, and
where for any
![]() $x\in X$
and
$x\in X$
and
![]() $n\geq 0$
, we define
$n\geq 0$
, we define
![]() $[x_1,\ldots ,x_n]:=\{y: y_k=x_k \textrm { for all} 1\leq k\leq n\}= B(x,2^{-n})$
to be the cylinder with prequel
$[x_1,\ldots ,x_n]:=\{y: y_k=x_k \textrm { for all} 1\leq k\leq n\}= B(x,2^{-n})$
to be the cylinder with prequel
![]() $(x_1,\ldots ,x_n)$
, thought of as a ball of radius
$(x_1,\ldots ,x_n)$
, thought of as a ball of radius
![]() $2^{-n}$
(the choice of center is arbitrary).
$2^{-n}$
(the choice of center is arbitrary).
For any collection
![]() $\mathcal {B} \subseteq \mathcal P(\mathcal {B}(X))$
of balls and for any
$\mathcal {B} \subseteq \mathcal P(\mathcal {B}(X))$
of balls and for any
![]() $R\in U$
, we will write
$R\in U$
, we will write
 $$ \begin{align*} \frac{1}{R} \mathcal{A}:= \bigcup_{A \in \mathcal{A}} \mathcal{S}(A, R). \end{align*} $$
$$ \begin{align*} \frac{1}{R} \mathcal{A}:= \bigcup_{A \in \mathcal{A}} \mathcal{S}(A, R). \end{align*} $$
Of course, for higher powers of R, we can write
![]() $1/{R^{n}} \mathcal {A} = 1/{R}(\cdots (1/{R}\mathcal {A})\cdots )$
.
$1/{R^{n}} \mathcal {A} = 1/{R}(\cdots (1/{R}\mathcal {A})\cdots )$
.
We can now recall the definition of generalized Cantor sets. Fix some closed ball
![]() $B_0 \subseteq X$
and some
$B_0 \subseteq X$
and some
![]() $R \in U$
, and let
$R \in U$
, and let
be a two-parameter sequence of non-negative real numbers. Define
![]() $\mathcal {B}_0:=\{B_0\}$
. We start by considering the set
$\mathcal {B}_0:=\{B_0\}$
. We start by considering the set
![]() $1/{R} \mathcal {B}_0$
. The first step in the construction of a generalized Cantor set involves the removal of a collection
$1/{R} \mathcal {B}_0$
. The first step in the construction of a generalized Cantor set involves the removal of a collection
![]() $\mathcal {A}_{0,0} $
of at most
$\mathcal {A}_{0,0} $
of at most
![]() $r_{0,0}$
balls from
$r_{0,0}$
balls from
![]() $1/{R}\mathcal {B}_0$
. We label the surviving collection as
$1/{R}\mathcal {B}_0$
. We label the surviving collection as
![]() $\mathcal {B}_1$
. Note that we do not specify here the removed balls, we just give an upper bound for their number. In general, for a fixed
$\mathcal {B}_1$
. Note that we do not specify here the removed balls, we just give an upper bound for their number. In general, for a fixed
![]() $n\geqslant 0$
, given the collection
$n\geqslant 0$
, given the collection
![]() $\mathcal {B}_n$
, we construct a nested collection
$\mathcal {B}_n$
, we construct a nested collection
![]() $\mathcal {B}_{n+1}$
as follows: let
$\mathcal {B}_{n+1}$
as follows: let
 $$ \begin{align} \mathcal{B}_{n+1}: = \bigg(\frac{1}{R} \mathcal{B}_n\bigg) \setminus \bigcup_{m=0}^n \mathcal{A}_{m,n} \quad \text{where } \mathcal{A}_{m,n} \subseteq \frac{1}{R^{n-m+1}} \mathcal{B}_m \quad (0 \leq m \leq n) \end{align} $$
$$ \begin{align} \mathcal{B}_{n+1}: = \bigg(\frac{1}{R} \mathcal{B}_n\bigg) \setminus \bigcup_{m=0}^n \mathcal{A}_{m,n} \quad \text{where } \mathcal{A}_{m,n} \subseteq \frac{1}{R^{n-m+1}} \mathcal{B}_m \quad (0 \leq m \leq n) \end{align} $$
are collections of removed balls satisfying for every
![]() $B \in \mathcal {B}_m$
, the inequality
$B \in \mathcal {B}_m$
, the inequality
For a pictorial demonstration in
![]() $\mathbb R^2$
of such a construction, see Figure 5, in which boxes removed in the current step are colored red.
$\mathbb R^2$
of such a construction, see Figure 5, in which boxes removed in the current step are colored red.

Figure 5 Construction of a Cantor winning set.
Define the limit set of such a construction to be
and denote it by
![]() $\mathcal {K}(B_0, R,\mathbf {r})$
. Note that the triple
$\mathcal {K}(B_0, R,\mathbf {r})$
. Note that the triple
![]() $(B_0,R,\mathbf {r})$
does not uniquely determine
$(B_0,R,\mathbf {r})$
does not uniquely determine
![]() $\mathcal {K}(B_0,R,\mathbf {r})$
as there is a large degree of freedom in the sets of balls
$\mathcal {K}(B_0,R,\mathbf {r})$
as there is a large degree of freedom in the sets of balls
![]() $\mathcal {A}_{m,n}$
removed in the construction procedure. We say a set
$\mathcal {A}_{m,n}$
removed in the construction procedure. We say a set
![]() $\mathcal {K}$
is a generalized Cantor set if it can be constructed by the procedure described above for some triple
$\mathcal {K}$
is a generalized Cantor set if it can be constructed by the procedure described above for some triple
![]() $(B_0,R,\mathbf {r})$
. In this case, we may refer to
$(B_0,R,\mathbf {r})$
. In this case, we may refer to
![]() $\mathcal {K}$
as being
$\mathcal {K}$
as being
![]() $(B_0,R,\mathbf {r})$
Cantor if we wish to make such a triple explicit and write
$(B_0,R,\mathbf {r})$
Cantor if we wish to make such a triple explicit and write
![]() $\mathcal {K}=\mathcal {K}(B_0,R,\mathbf {r})$
.
$\mathcal {K}=\mathcal {K}(B_0,R,\mathbf {r})$
.
Example 2.8. In the case that
![]() $r_{m,n}=0$
for every
$r_{m,n}=0$
for every
![]() $m < n$
, we refer to a
$m < n$
, we refer to a
![]() $(B_0,R,\mathbf {r})$
Cantor set as a local Cantor set and denote it simply by
$(B_0,R,\mathbf {r})$
Cantor set as a local Cantor set and denote it simply by
![]() $\mathcal {K}(B_0,R, \{r_n\})$
, where
$\mathcal {K}(B_0,R, \{r_n\})$
, where
![]() $r_n:=r_{n,n}$
. The simplest class of local Cantor sets occurs when the sequence
$r_n:=r_{n,n}$
. The simplest class of local Cantor sets occurs when the sequence
![]() $\{r_n\}$
is taken to be constant; that is,
$\{r_n\}$
is taken to be constant; that is,
![]() $r_n:=r$
. Such
$r_n:=r$
. Such
![]() $(B_0,R, r)$
Cantor sets are well studied and their measure theoretic properties are well known.
$(B_0,R, r)$
Cantor sets are well studied and their measure theoretic properties are well known.
Example 2.9. The middle-third Cantor set
![]() $\mathcal {K}$
is an
$\mathcal {K}$
is an
![]() $(I,3,1)$
Cantor set in
$(I,3,1)$
Cantor set in
![]() $\mathbb {R}$
, and
$\mathbb {R}$
, and
![]() $\mathcal {K}^2$
is a
$\mathcal {K}^2$
is a
![]() $(I^2,3,5)$
Cantor set in
$(I^2,3,5)$
Cantor set in
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
Definition 2.10. Fix a ball
![]() $B_0 \subseteq X$
. Given a parameter
$B_0 \subseteq X$
. Given a parameter
![]() $\varepsilon _0 \in (0,1]$
, we say a set
$\varepsilon _0 \in (0,1]$
, we say a set
![]() $E \subseteq X$
is
$E \subseteq X$
is
![]() $\varepsilon _0$
Cantor winning on
$\varepsilon _0$
Cantor winning on
![]() $B_0$
(with respect to the splitting structure
$B_0$
(with respect to the splitting structure
![]() $(X, \mathcal {S}, U, f)$
) if for every
$(X, \mathcal {S}, U, f)$
) if for every
![]() $0<\varepsilon <\varepsilon _0$
, there exists
$0<\varepsilon <\varepsilon _0$
, there exists
![]() $R_\varepsilon \in U$
such that for every
$R_\varepsilon \in U$
such that for every
![]() $R_\varepsilon \leq R\in U$
, the set E contains a
$R_\varepsilon \leq R\in U$
, the set E contains a
![]() $(B_0,R,\mathbf {r})$
Cantor set satisfying
$(B_0,R,\mathbf {r})$
Cantor set satisfying
If a set
![]() $E \subseteq X$
is
$E \subseteq X$
is
![]() $\varepsilon _0$
Cantor winning on
$\varepsilon _0$
Cantor winning on
![]() $B_0$
for every ball
$B_0$
for every ball
![]() $B_0\subseteq X$
, then we say E is
$B_0\subseteq X$
, then we say E is
![]() $\varepsilon _0$
Cantor winning, and simply that E is Cantor winning if it is
$\varepsilon _0$
Cantor winning, and simply that E is Cantor winning if it is
![]() $\varepsilon _0$
Cantor winning for some
$\varepsilon _0$
Cantor winning for some
![]() $\varepsilon _0 \in (0,1]$
.
$\varepsilon _0 \in (0,1]$
.
It is obvious that if a set is
![]() $\varepsilon _0$
Cantor winning, then it is also
$\varepsilon _0$
Cantor winning, then it is also
![]() $\varepsilon $
Cantor winning for any
$\varepsilon $
Cantor winning for any
![]() $\varepsilon \in (0, \varepsilon _0)$
. In particular, the property of being
$\varepsilon \in (0, \varepsilon _0)$
. In particular, the property of being
![]() $1$
Cantor winning is the strongest possible Cantor winning property.
$1$
Cantor winning is the strongest possible Cantor winning property.
Remark 2.11. As for the generalized Cantor sets, whenever we mention Cantor winning sets not in the context of a splitting structure, we will refer to a standard splitting structure. In particular, this applies to all theorems in §1.2 where the standard splitting structure in
![]() $\mathbb {R}^N$
is considered. Some of those results remain true in a more general context of complete metric spaces.
$\mathbb {R}^N$
is considered. Some of those results remain true in a more general context of complete metric spaces.
2.6. Cantor rich
The class of Cantor rich subsets of
![]() $\mathbb {R}$
was introduced in [Reference Beresnevich8]. As was noted in [Reference Badziahin and Harrap5], this notion can be generalized to the context of metric spaces endowed with a splitting structure.
$\mathbb {R}$
was introduced in [Reference Beresnevich8]. As was noted in [Reference Badziahin and Harrap5], this notion can be generalized to the context of metric spaces endowed with a splitting structure.
Definition 2.12. Let
![]() $M\geq 4$
be a real number and
$M\geq 4$
be a real number and
![]() $B_0$
be a ball in X. A set
$B_0$
be a ball in X. A set
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $(B_{0},M)$
Cantor rich if for every R such that
$(B_{0},M)$
Cantor rich if for every R such that
and
![]() $0 < y < 1$
, E contains a
$0 < y < 1$
, E contains a
![]() $(B_{0},R,\mathbf {r})$
Cantor set, where
$(B_{0},R,\mathbf {r})$
Cantor set, where
![]() $\mathbf {r} = (r_{m,n})_{0\leq m\leq n}$
is a two-parameter sequence satisfying
$\mathbf {r} = (r_{m,n})_{0\leq m\leq n}$
is a two-parameter sequence satisfying
 $$ \begin{align*} \sum_{m=0}^{n}\bigg(\frac{4}{f(R)}\bigg)^{n-m+1}r_{m,n}\leq y\quad\text{for every }n\geq0. \end{align*} $$
$$ \begin{align*} \sum_{m=0}^{n}\bigg(\frac{4}{f(R)}\bigg)^{n-m+1}r_{m,n}\leq y\quad\text{for every }n\geq0. \end{align*} $$
Here, E is Cantor rich in
![]() $B_{0}$
if it is
$B_{0}$
if it is
![]() $(B_{0},M)$
Cantor rich in
$(B_{0},M)$
Cantor rich in
![]() $B_{0}$
for some
$B_{0}$
for some
![]() $M\geq 4$
, and E is Cantor rich if it is Cantor rich in some
$M\geq 4$
, and E is Cantor rich if it is Cantor rich in some
![]() $B_{0}$
.
$B_{0}$
.
Note that, following [Reference Beresnevich8], Cantor rich sets are Cantor rich in some ball, while Cantor winning sets are Cantor winning in every ball. Also note that unlike in [Reference Beresnevich8], the inequality in equation (12) is strict. This enables a clearer correspondence with the parameter
![]() $\varepsilon _0$
in Definition 2.10 (cf. Corollary 3.11).
$\varepsilon _0$
in Definition 2.10 (cf. Corollary 3.11).
2.7. Diffuse sets and doubling spaces
Schmidt’s game was originally played on a complete metric space. However, to conclude that winning sets have properties such as large Hausdorff dimension, certain assumptions on the underlying space are required. The first time that large intersection with certain subspaces of
![]() $\mathbb {R}^n$
was proved using Schmidt’s game was in [Reference Fishman24]. Later, it was realized in [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11] that, more generally, some spaces form a natural playground for the absolute game. The following notion generalizes the definition of a diffuse set in
$\mathbb {R}^n$
was proved using Schmidt’s game was in [Reference Fishman24]. Later, it was realized in [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11] that, more generally, some spaces form a natural playground for the absolute game. The following notion generalizes the definition of a diffuse set in
![]() $\mathbb {R}^n$
as appeared in [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11].
$\mathbb {R}^n$
as appeared in [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11].
Definition 2.13. For
![]() $0<\beta <1$
, a closed set
$0<\beta <1$
, a closed set
![]() $K\subseteq X$
is
$K\subseteq X$
is
![]() $\beta $
diffuse if there exists
$\beta $
diffuse if there exists
![]() $r_{0}>0$
such that for every
$r_{0}>0$
such that for every
![]() $x\in K$
,
$x\in K$
,
![]() $y\in X$
and
$y\in X$
and
![]() $0<r\leq r_{0}$
, we have
$0<r\leq r_{0}$
, we have
If K is
![]() $\beta $
diffuse for some
$\beta $
diffuse for some
![]() $\beta $
, then we say it is diffuse.
$\beta $
, then we say it is diffuse.
The condition in equation (13) is satisfied if and only if there exists
![]() $z\in K$
such that
$z\in K$
such that
The definition of diffuse sets is designed so that the
![]() $\beta $
absolute game on a
$\beta $
absolute game on a
![]() $\beta $
diffuse metric space cannot end after finitely many steps (as long as the first ball of Bob is small enough). So, if Alice plays the game in such way that she is able to force the outcome to lie in the target set, then the reason for her victory is her strategy and not the limitations of the space in which the game is played.
$\beta $
diffuse metric space cannot end after finitely many steps (as long as the first ball of Bob is small enough). So, if Alice plays the game in such way that she is able to force the outcome to lie in the target set, then the reason for her victory is her strategy and not the limitations of the space in which the game is played.
Remark 2.14. In the definition that appears in [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11], sets as in Definition 2.13 are called
![]() $0$
-dimensionally diffuse. Moreover, equation (13) is replaced by
$0$
-dimensionally diffuse. Moreover, equation (13) is replaced by
Note that
for
![]() $\beta '={\beta }/({2+\beta })$
and
$\beta '={\beta }/({2+\beta })$
and
![]() $\rho =(1+{\beta }/{2})r$
, so both equations (13) and (14) give rise to the same class of diffuse sets. We will use equations (13) and (14) interchangeably without further notice.
$\rho =(1+{\beta }/{2})r$
, so both equations (13) and (14) give rise to the same class of diffuse sets. We will use equations (13) and (14) interchangeably without further notice.
A more standard definition that is equivalent to diffuseness (see [Reference Fishman, Simmons and Urbański26, Lemma 4.3]) is the following.
Definition 2.15. For
![]() $0<c<1$
, a closed set
$0<c<1$
, a closed set
![]() $K\subseteq X$
is c uniformly perfect if there exists
$K\subseteq X$
is c uniformly perfect if there exists
![]() $r_{0}>0$
such that for every
$r_{0}>0$
such that for every
![]() $x\in K$
and
$x\in K$
and
![]() $0<r\leq r_{0}$
, we have
$0<r\leq r_{0}$
, we have
If K is c uniformly perfect for some c, then we say it is uniformly perfect.
Being diffuse is equivalent to having no singletons as microsets [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11, Lemma 4.4]. Instead of expanding the discussion on microsets, we refer the interested reader to [Reference Furstenberg27], and mention that Ahlfors regular sets are diffuse. In the other direction, diffuse sets support Ahlfors regular measures (see Proposition 2.18). We will now give the relevant definitions and provide the results which support the statements above.
Definition 2.16. A Borel measure
![]() $\mu $
on X is called Ahlfors regular if there exist
$\mu $
on X is called Ahlfors regular if there exist
![]() $C,\delta ,r_{0}>0$
such that every x in the support of
$C,\delta ,r_{0}>0$
such that every x in the support of
![]() $\mu $
and
$\mu $
and
![]() $0<r\leq r_{0}$
satisfy
$0<r\leq r_{0}$
satisfy
In this case, we call
![]() $\delta $
the dimension of
$\delta $
the dimension of
![]() $\mu $
and say that
$\mu $
and say that
![]() $\mu $
is Ahlfors regular of dimension
$\mu $
is Ahlfors regular of dimension
![]() $\delta $
.
$\delta $
.
We say that a closed set
![]() $K\subseteq X$
is Ahlfors regular if it is the support of an Ahlfors regular measure. More exactly,
$K\subseteq X$
is Ahlfors regular if it is the support of an Ahlfors regular measure. More exactly,
![]() $K\subseteq X$
is
$K\subseteq X$
is
![]() $\delta $
Ahlfors regular if it is the support of an Ahlfors regular measure of dimension
$\delta $
Ahlfors regular if it is the support of an Ahlfors regular measure of dimension
![]() $\delta $
. This terminology gives rise to a dimensional property of K.
$\delta $
. This terminology gives rise to a dimensional property of K.
Definition 2.17. The Ahlfors regularity dimension of
![]() $K\subseteq X$
is
$K\subseteq X$
is
Note that it is a direct consequence of the mass distribution principle (see [Reference Falconer19]) that
![]() $\dim _R K\leq \dim _H K$
, where
$\dim _R K\leq \dim _H K$
, where
![]() $\dim _H K$
stands for the Hausdorff dimension of K.
$\dim _H K$
stands for the Hausdorff dimension of K.
Proposition 2.18. A diffuse set
![]() $K\subseteq X$
satisfies
$K\subseteq X$
satisfies
![]() $\dim _R K>0$
. Conversely, if
$\dim _R K>0$
. Conversely, if
![]() $\dim _R K> 0$
, then K contains a diffuse set.
$\dim _R K> 0$
, then K contains a diffuse set.
Proof. Suppose K is
![]() $\beta $
diffuse; then every ball in K of radius
$\beta $
diffuse; then every ball in K of radius
![]() $\rho $
contains two disjoint balls of radius
$\rho $
contains two disjoint balls of radius
![]() $\beta \rho $
. Construct a Cantor set by recursively replacing every ball of radius
$\beta \rho $
. Construct a Cantor set by recursively replacing every ball of radius
![]() $\rho $
with two disjoint subballs of radius
$\rho $
with two disjoint subballs of radius
![]() $\beta \rho $
. Standard calculations show that this Cantor set is Ahlfors regular of dimension
$\beta \rho $
. Standard calculations show that this Cantor set is Ahlfors regular of dimension
![]() $({\log 2})/({-\log \beta })> 0$
, so
$({\log 2})/({-\log \beta })> 0$
, so
![]() $\dim _R K> 0$
.
$\dim _R K> 0$
.
Suppose
![]() $\dim _R K> 0$
; then K contains an Ahlfors regular subset of positive dimension, which is diffuse (cf. e.g. [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11, Lemma 5.1]).
$\dim _R K> 0$
; then K contains an Ahlfors regular subset of positive dimension, which is diffuse (cf. e.g. [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11, Lemma 5.1]).
The following property of Ahlfors regular sets will be used later in the paper.
Proposition 2.19. If
![]() $(X,\mu )$
is
$(X,\mu )$
is
![]() $\delta $
Ahlfors regular, then there exists
$\delta $
Ahlfors regular, then there exists
![]() $c>0$
such that for any ball
$c>0$
such that for any ball
![]() $B\subseteq X$
and any
$B\subseteq X$
and any
![]() $\alpha <1$
, there exist at least
$\alpha <1$
, there exist at least
![]() $c\alpha ^{-\delta }$
balls
$c\alpha ^{-\delta }$
balls
![]() $B_i=B(x_i,\alpha \cdot \mathrm {rad}(B))\subseteq B (i\in \{1,\ldots , I\}, I\geqslant c\alpha ^{-\delta })$
such that
$B_i=B(x_i,\alpha \cdot \mathrm {rad}(B))\subseteq B (i\in \{1,\ldots , I\}, I\geqslant c\alpha ^{-\delta })$
such that
![]() $\mathbf {d} (x_i,x_j)\geqslant 3\alpha \cdot \mathrm {rad}(B)$
for any
$\mathbf {d} (x_i,x_j)\geqslant 3\alpha \cdot \mathrm {rad}(B)$
for any
![]() $1\leqslant i\neq j\leqslant I$
.
$1\leqslant i\neq j\leqslant I$
.
Proof. It is enough to prove the proposition for all
![]() $\alpha \leq 1/2$
. Let
$\alpha \leq 1/2$
. Let
![]() $B'$
be a ball with the same center as B, but with radius
$B'$
be a ball with the same center as B, but with radius
![]() $(1-\alpha )\mathrm {rad}(B)$
, and let
$(1-\alpha )\mathrm {rad}(B)$
, and let
![]() $D\subseteq X$
be an arbitrary ball of radius
$D\subseteq X$
be an arbitrary ball of radius
![]() $\mathrm {rad}(D) = 3\alpha \cdot \mathrm {rad}(B)$
. Then
$\mathrm {rad}(D) = 3\alpha \cdot \mathrm {rad}(B)$
. Then
 $$ \begin{align*} \mu (D)\leqslant C\cdot (3\alpha)^\delta (\mathrm{rad}(B))^\delta \leqslant C^2\cdot \bigg(\frac{3\alpha}{1-\alpha}\bigg)^\delta \mu (B') \leq C_1 \alpha^\delta \mu (B'). \end{align*} $$
$$ \begin{align*} \mu (D)\leqslant C\cdot (3\alpha)^\delta (\mathrm{rad}(B))^\delta \leqslant C^2\cdot \bigg(\frac{3\alpha}{1-\alpha}\bigg)^\delta \mu (B') \leq C_1 \alpha^\delta \mu (B'). \end{align*} $$
Therefore, for any k balls
![]() $D_i$
of radius
$D_i$
of radius
![]() $3\alpha \cdot \mathrm {rad}(B)$
with
$3\alpha \cdot \mathrm {rad}(B)$
with
![]() $k<C_1^{-1} \alpha ^{-\delta }$
, there exists another ball D whose center lies inside
$k<C_1^{-1} \alpha ^{-\delta }$
, there exists another ball D whose center lies inside
![]() $B'\backslash \bigcup _{i=1}^k D_i$
. Hence, there are at least
$B'\backslash \bigcup _{i=1}^k D_i$
. Hence, there are at least
![]() $I = \lceil C_1^{-1} \alpha ^{-\delta }\rceil $
balls
$I = \lceil C_1^{-1} \alpha ^{-\delta }\rceil $
balls
![]() $D_i$
such that their centers lie inside
$D_i$
such that their centers lie inside
![]() $B'$
and are distanced by at least
$B'$
and are distanced by at least
![]() $3 \alpha \cdot \mathrm {rad}(B)$
from each other. For each
$3 \alpha \cdot \mathrm {rad}(B)$
from each other. For each
![]() $1 \leq i \leq I$
, let
$1 \leq i \leq I$
, let
![]() $B_i$
be a ball with the same center as of
$B_i$
be a ball with the same center as of
![]() $D_i$
but with the radius
$D_i$
but with the radius
![]() $\alpha \cdot \mathrm {rad}(B)$
. Clearly, the balls
$\alpha \cdot \mathrm {rad}(B)$
. Clearly, the balls
![]() $B_i$
satisfy all the conditions of the proposition, where
$B_i$
satisfy all the conditions of the proposition, where
![]() $c>0$
is chosen to ensure the inequality
$c>0$
is chosen to ensure the inequality
for all
![]() $\alpha \in [0,1]$
.
$\alpha \in [0,1]$
.
Although winning sets are usually dense, the large dimension property (W1) for some types of winning sets depends on the space X being large enough. For example, absolute winning sets may be empty if the Ahlfors regularity dimension is zero (cf. Remark 4.9). Various conditions are introduced in this context; for example, see [Reference Schmidt37, §11] and [Reference Fishman24, Theorem 3.1]. More recently, the following condition was introduced in [Reference Badziahin and Harrap5].
-
(S4) There exists an absolute constant
 $C(X)$
such that any ball
$C(X)$
such that any ball
 $B \in \mathcal {B}(X)$
cannot intersect more than
$B \in \mathcal {B}(X)$
cannot intersect more than
 $C(X)$
disjoint open balls of the same radius as B.
$C(X)$
disjoint open balls of the same radius as B.
Proposition 2.20. [Reference Badziahin and Harrap5, Corollary to Theorem 4.1]
Let X be a complete metric space and let
![]() $(X,\mathcal {S}, U,f)$
be a splitting structure. If X satisfies (S4), then for any
$(X,\mathcal {S}, U,f)$
be a splitting structure. If X satisfies (S4), then for any
![]() $B \in \mathcal {B}(X)$
and any Cantor winning set
$B \in \mathcal {B}(X)$
and any Cantor winning set
![]() $E\subseteq X$
, we have
$E\subseteq X$
, we have
Condition (S4) is similar to the following definition.
Definition 2.21. A metric space X is doubling if there exists a constant
![]() $N\in \mathbb {N}$
such that for every
$N\in \mathbb {N}$
such that for every
![]() $r>0$
, every ball of radius
$r>0$
, every ball of radius
![]() $2 r$
can be covered by a collection of at most N balls of radius r.
$2 r$
can be covered by a collection of at most N balls of radius r.
Doubling spaces satisfy condition (S4), but the converse does not hold. For example, in an ultrametric space, any two non-disjoint balls of the same radius are set-theoretically equal. So an ultrametric space satisfies condition (S4) with
![]() $C=1$
, but is not necessarily doubling. As shown in [Reference Badziahin and Harrap5], the space X needs to satisfy condition (S4) for Cantor winning sets in X to satisfy the large dimension condition (W1) and large intersection condition (W2), and if X is doubling, then Cantor winning sets satisfy condition (W3) with respect to bi-Lipschitz homeomorphisms of X. This makes doubling spaces a natural setting for generalized Cantor sets, and it is under this condition that many of the results of the next section hold.
$C=1$
, but is not necessarily doubling. As shown in [Reference Badziahin and Harrap5], the space X needs to satisfy condition (S4) for Cantor winning sets in X to satisfy the large dimension condition (W1) and large intersection condition (W2), and if X is doubling, then Cantor winning sets satisfy condition (W3) with respect to bi-Lipschitz homeomorphisms of X. This makes doubling spaces a natural setting for generalized Cantor sets, and it is under this condition that many of the results of the next section hold.
3. Connections
3.1. The Cantor game
To facilitate a more natural exposition, we introduce a new game. The ‘Cantor game’ described below is similar to the games described earlier. The main difference is that this game is designed to be played on a metric space endowed with a splitting structure. Our nomenclature is so chosen because (as we shall demonstrate) under natural conditions, the winning sets for this game are precisely the Cantor winning sets defined in Definition 2.10.
Let X be a complete metric space and let
![]() $(X,\mathcal {S}, U,f)$
be a splitting structure. Given
$(X,\mathcal {S}, U,f)$
be a splitting structure. Given
![]() $\varepsilon \in (0,1]$
, the
$\varepsilon \in (0,1]$
, the
![]() $\varepsilon $
Cantor game is defined as follows: Bob starts by choosing an integer
$\varepsilon $
Cantor game is defined as follows: Bob starts by choosing an integer
![]() $2\leq R\in U$
and a closed ball
$2\leq R\in U$
and a closed ball
![]() $B_0\subseteq X$
. For any
$B_0\subseteq X$
. For any
![]() $i\geq 0$
, given Bob’s ith choice
$i\geq 0$
, given Bob’s ith choice
![]() $B_i$
, Alice chooses a collection
$B_i$
, Alice chooses a collection
![]() $\mathcal {A}_{i+1}\subseteq {1}/{R}\{B_i\}$
satisfying
$\mathcal {A}_{i+1}\subseteq {1}/{R}\{B_i\}$
satisfying
Given
![]() $\mathcal {A}_{i+1}$
, Bob chooses a ball
$\mathcal {A}_{i+1}$
, Bob chooses a ball
![]() $B_{i+1}\in {1}/{R}\{B_i\}\setminus \mathcal {A}_{i+1}$
, and the game continues. We say that
$B_{i+1}\in {1}/{R}\{B_i\}\setminus \mathcal {A}_{i+1}$
, and the game continues. We say that
![]() $E\subseteq X$
is winning for the
$E\subseteq X$
is winning for the
![]() $\varepsilon $
Cantor game if Alice has a strategy which guarantees that equation (3) is satisfied. The Cantor game is defined by allowing Alice first to choose
$\varepsilon $
Cantor game if Alice has a strategy which guarantees that equation (3) is satisfied. The Cantor game is defined by allowing Alice first to choose
![]() $\varepsilon \in (0,1]$
and then continuing as in the
$\varepsilon \in (0,1]$
and then continuing as in the
![]() $\varepsilon $
Cantor game. We say that E is winning for the Cantor game if Alice has a winning strategy for the Cantor game. Note that E is winning for the Cantor game if and only if it is winning for the
$\varepsilon $
Cantor game. We say that E is winning for the Cantor game if Alice has a winning strategy for the Cantor game. Note that E is winning for the Cantor game if and only if it is winning for the
![]() $\varepsilon $
Cantor game for some
$\varepsilon $
Cantor game for some
![]() $\varepsilon \in (0,1]$
. We say that E is winning for the
$\varepsilon \in (0,1]$
. We say that E is winning for the
![]() $\varepsilon $
Cantor game on
$\varepsilon $
Cantor game on
![]() $B_0$
if Alice has a winning strategy in the
$B_0$
if Alice has a winning strategy in the
![]() $\varepsilon $
Cantor game given that Bob’s first ball is
$\varepsilon $
Cantor game given that Bob’s first ball is
![]() $B_0$
.
$B_0$
.
Remark 3.1. A version of the Cantor game may be played in metric spaces with no prescribed splitting structure. Given
![]() $c\geq 0$
and
$c\geq 0$
and
![]() $0<\beta <1$
, Bob will choose a sequence of decreasing balls with radii that shrink at rate
$0<\beta <1$
, Bob will choose a sequence of decreasing balls with radii that shrink at rate
![]() $\beta $
, while Alice will remove a collection of at most
$\beta $
, while Alice will remove a collection of at most
![]() $\beta ^{-c}$
closed balls of radius
$\beta ^{-c}$
closed balls of radius
![]() $\beta r$
where r is the radius of Bob’s previous choice, instead of just one such ball as in the absolute game. When
$\beta r$
where r is the radius of Bob’s previous choice, instead of just one such ball as in the absolute game. When
![]() $c=0$
, this game coincides with the absolute game.
$c=0$
, this game coincides with the absolute game.
It is clear that winning sets for the Cantor game contain Cantor winning sets. Indeed, by the construction, for any
![]() $R\in U$
, a winning set for the
$R\in U$
, a winning set for the
![]() $\varepsilon $
Cantor game on
$\varepsilon $
Cantor game on
![]() $B_0$
contains a
$B_0$
contains a
![]() $(B_0, R, f(R)^{1-\varepsilon })$
Cantor set which comprises all Bob’s possible moves while playing against a fixed winning strategy of Alice. Therefore, it is
$(B_0, R, f(R)^{1-\varepsilon })$
Cantor set which comprises all Bob’s possible moves while playing against a fixed winning strategy of Alice. Therefore, it is
![]() $\varepsilon $
Cantor winning on
$\varepsilon $
Cantor winning on
![]() $B_0$
. We show that the converse is also true.
$B_0$
. We show that the converse is also true.
Theorem 3.2. Let
![]() $E\subseteq X$
. Let
$E\subseteq X$
. Let
![]() $B_{0}\subseteq X$
be a closed ball and
$B_{0}\subseteq X$
be a closed ball and
![]() $0<\varepsilon _0\leq 1$
. If E is
$0<\varepsilon _0\leq 1$
. If E is
![]() $\varepsilon _0$
Cantor winning on
$\varepsilon _0$
Cantor winning on
![]() $B_0$
, then E is winning for the
$B_0$
, then E is winning for the
![]() $\varepsilon _0$
Cantor game on
$\varepsilon _0$
Cantor game on
![]() $B_0$
.
$B_0$
.
Proof. We will define a winning strategy for Alice. Fix
![]() $R\geq 2$
and let
$R\geq 2$
and let
![]() $\delta \geq 0$
be chosen so that
$\delta \geq 0$
be chosen so that
![]() $f(R) = R^\delta $
. Choose
$f(R) = R^\delta $
. Choose
![]() $0<\eta <\varepsilon _0$
so small that
$0<\eta <\varepsilon _0$
so small that
 $$ \begin{align*} \frac{R^{\delta(1-\varepsilon_0 + \eta)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1} < 1. \end{align*} $$
$$ \begin{align*} \frac{R^{\delta(1-\varepsilon_0 + \eta)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1} < 1. \end{align*} $$
Set
and let
![]() $R_{\varepsilon _1}$
be as in Definition 2.10. Then, for any
$R_{\varepsilon _1}$
be as in Definition 2.10. Then, for any
![]() $\ell $
such that
$\ell $
such that
![]() $R^\ell \geq R_{\varepsilon _1}$
, since
$R^\ell \geq R_{\varepsilon _1}$
, since
![]() $f(R^\ell )=f(R)^\ell =R^{\delta \ell }$
, there exists a
$f(R^\ell )=f(R)^\ell =R^{\delta \ell }$
, there exists a
![]() $(B_{0},R^\ell ,(R^{(n-m+1)\ell \delta (1-\varepsilon _1)})_{0\leq m\leq n})$
Cantor set in E. Let
$(B_{0},R^\ell ,(R^{(n-m+1)\ell \delta (1-\varepsilon _1)})_{0\leq m\leq n})$
Cantor set in E. Let
![]() $\ell $
be large enough so that
$\ell $
be large enough so that
![]() $R^{\ell }\geq R_{\varepsilon _1}$
,
$R^{\ell }\geq R_{\varepsilon _1}$
,
 $$ \begin{align} \bigg(\frac{R^{\delta(1-\varepsilon_2)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^\ell<\frac{1}{2}, \end{align} $$
$$ \begin{align} \bigg(\frac{R^{\delta(1-\varepsilon_2)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^\ell<\frac{1}{2}, \end{align} $$
and
Such a value exists because of the choice of
![]() $\eta $
.
$\eta $
.
Choose a
![]() $(B_{0},R^{\ell },(R^{(n-m+1)\ell \delta (1-\varepsilon _1)})_{0\leq m\leq n})$
Cantor set in E. Let
$(B_{0},R^{\ell },(R^{(n-m+1)\ell \delta (1-\varepsilon _1)})_{0\leq m\leq n})$
Cantor set in E. Let
![]() $\mathcal {A}=\{ \mathcal {A}_{m,n}\} _{0\leq m\leq n}$
be the removed balls, so that
$\mathcal {A}=\{ \mathcal {A}_{m,n}\} _{0\leq m\leq n}$
be the removed balls, so that
![]() $\mathcal {B}_{n+1}=({1}/{R^{\ell }})\mathcal {B}_{n}\setminus \bigcup _{m=0}^{n}\mathcal {A}_{m,n}$
for all
$\mathcal {B}_{n+1}=({1}/{R^{\ell }})\mathcal {B}_{n}\setminus \bigcup _{m=0}^{n}\mathcal {A}_{m,n}$
for all
![]() $n\geq 0$
, where
$n\geq 0$
, where
![]() $\mathcal {B}_{0}=\{ B_{0}\} $
.
$\mathcal {B}_{0}=\{ B_{0}\} $
.
Define a winning strategy for Alice in the
![]() $\varepsilon _0$
Cantor game as follows. For each
$\varepsilon _0$
Cantor game as follows. For each
![]() $i\geq 0$
, define a potential function on balls:
$i\geq 0$
, define a potential function on balls:
 $$ \begin{align} \varphi_{i}(B)=\sum_{m=0}^{\lfloor i/\ell\rfloor }\sum_{n=m}^{\infty}\#\{ A\in\mathcal{A}_{m,n}: A\cap B \text{ has non-empty interior}\} R^{-(n+1)\ell\delta(1 - \varepsilon_2)}. \end{align} $$
$$ \begin{align} \varphi_{i}(B)=\sum_{m=0}^{\lfloor i/\ell\rfloor }\sum_{n=m}^{\infty}\#\{ A\in\mathcal{A}_{m,n}: A\cap B \text{ has non-empty interior}\} R^{-(n+1)\ell\delta(1 - \varepsilon_2)}. \end{align} $$
Given Bob’s ith move
![]() $B_i$
, Alice’s strategy is to choose the subcollection
$B_i$
, Alice’s strategy is to choose the subcollection
![]() $\mathcal {A}_{i+1} \subseteq {1}/{R}\{B_i\}$
consisting of the
$\mathcal {A}_{i+1} \subseteq {1}/{R}\{B_i\}$
consisting of the
![]() $\lfloor R^{\delta (1-\varepsilon _0)} \rfloor $
balls with the largest corresponding values of
$\lfloor R^{\delta (1-\varepsilon _0)} \rfloor $
balls with the largest corresponding values of
![]() $\varphi _{i+1}$
. We will show that this is a winning strategy for Alice. Assume Bob chose the sequence of balls
$\varphi _{i+1}$
. We will show that this is a winning strategy for Alice. Assume Bob chose the sequence of balls
![]() $\{B_i\}_{i=0}^\infty $
on his turns, while Alice responded according to the above strategy. It is enough to prove that for every
$\{B_i\}_{i=0}^\infty $
on his turns, while Alice responded according to the above strategy. It is enough to prove that for every
![]() $i\geq 0$
,
$i\geq 0$
,
Indeed, this inequality would imply that
![]() $B_{i\ell }$
does not intersect any of the balls from
$B_{i\ell }$
does not intersect any of the balls from
![]() $\mathcal {A}_{m,n}$
with
$\mathcal {A}_{m,n}$
with
![]() $n<i$
except at the boundary, which implies that
$n<i$
except at the boundary, which implies that
![]() $B_{i\ell }\in \mathcal {B}_i$
.
$B_{i\ell }\in \mathcal {B}_i$
.
Fix
![]() $i\geq 0$
such that equation (21) holds. For every
$i\geq 0$
such that equation (21) holds. For every
![]() $0\leq j\leq \ell -1$
, note that
$0\leq j\leq \ell -1$
, note that
![]() $\lfloor ({i\ell +j})/({\ell })\rfloor = i$
, so by the induction hypothesis in equation (21), we get
$\lfloor ({i\ell +j})/({\ell })\rfloor = i$
, so by the induction hypothesis in equation (21), we get
Therefore, for any
![]() $n\geq m \geq 0$
, if
$n\geq m \geq 0$
, if
![]() $A\in \mathcal {A}_{m,n}$
is such that
$A\in \mathcal {A}_{m,n}$
is such that
![]() $A\cap B_{i\ell +j+1}$
has non-empty interior, then necessarily
$A\cap B_{i\ell +j+1}$
has non-empty interior, then necessarily
![]() $n+1> i$
, and thus by condition (S2), we have
$n+1> i$
, and thus by condition (S2), we have
![]() $A \subseteq B_{i\ell +j+1}$
. So
$A \subseteq B_{i\ell +j+1}$
. So
 $$ \begin{align} \sum_{A\in\frac{1}{R}\{B_{i\ell+j}\}}\varphi_{i\ell+j}(A)=\varphi_{i\ell+j}(B_{i\ell+ j}), \end{align} $$
$$ \begin{align} \sum_{A\in\frac{1}{R}\{B_{i\ell+j}\}}\varphi_{i\ell+j}(A)=\varphi_{i\ell+j}(B_{i\ell+ j}), \end{align} $$
and the definition of Alice’s strategy yields
for every
![]() $0\leq j\leq l-1$
. Indeed, there are at least
$0\leq j\leq l-1$
. Indeed, there are at least
![]() $\lfloor R^{\delta (1-\varepsilon _0)}\rfloor $
balls A, chosen by Alice in her turn, with
$\lfloor R^{\delta (1-\varepsilon _0)}\rfloor $
balls A, chosen by Alice in her turn, with
![]() $\varphi _{i\ell +j}(A)\geqslant \varphi _{i\ell +j}(B_{i\ell +j+1})$
. Therefore, if equation (23) fails for some ball
$\varphi _{i\ell +j}(A)\geqslant \varphi _{i\ell +j}(B_{i\ell +j+1})$
. Therefore, if equation (23) fails for some ball
![]() $B_{i\ell +j+1}$
, we have
$B_{i\ell +j+1}$
, we have
 $$ \begin{align*} \varphi_{i\ell+j}(B_{i\ell+j+1}) + \sum_{A\text{ chosen by Alice}} \varphi_{i\ell+j}(A)> \varphi_{i\ell+j}(B_{i\ell+j}) \end{align*} $$
$$ \begin{align*} \varphi_{i\ell+j}(B_{i\ell+j+1}) + \sum_{A\text{ chosen by Alice}} \varphi_{i\ell+j}(A)> \varphi_{i\ell+j}(B_{i\ell+j}) \end{align*} $$
which contradicts equation (22).
To estimate
![]() $\varphi _{(i+1)\ell }(B_{(i+1)\ell })$
, we need to additionally consider the potential coming from the sets
$\varphi _{(i+1)\ell }(B_{(i+1)\ell })$
, we need to additionally consider the potential coming from the sets
![]() $(\mathcal {A}_{i+1,n})_{n\geqslant i+1}$
. Clearly, for any
$(\mathcal {A}_{i+1,n})_{n\geqslant i+1}$
. Clearly, for any
![]() $A\in \mathcal {A}_{i+1,n}$
, the condition that
$A\in \mathcal {A}_{i+1,n}$
, the condition that
![]() $A\cap B_{(i+1)\ell }$
has non-empty interior is equivalent to the inclusion
$A\cap B_{(i+1)\ell }$
has non-empty interior is equivalent to the inclusion
![]() $A\subseteq B_{(i+1)\ell }$
. Hence, we have
$A\subseteq B_{(i+1)\ell }$
. Hence, we have
 $$ \begin{align*} \varphi_{(i+1)\ell}(B_{(i+1)\ell}) \leq & \bigg(\frac{1}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}\varphi_{i\ell}(B_{i\ell}) \\ & + \sum_{n=i+1}^{\infty}\#\{ A\in\mathcal{A}_{i+1,n}: A\subseteq B_{(i+1)\ell}\} R^{-(n+1)\ell\delta(1-\varepsilon_2)}. \end{align*} $$
$$ \begin{align*} \varphi_{(i+1)\ell}(B_{(i+1)\ell}) \leq & \bigg(\frac{1}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}\varphi_{i\ell}(B_{i\ell}) \\ & + \sum_{n=i+1}^{\infty}\#\{ A\in\mathcal{A}_{i+1,n}: A\subseteq B_{(i+1)\ell}\} R^{-(n+1)\ell\delta(1-\varepsilon_2)}. \end{align*} $$
Since
![]() $\#\{ A\in \mathcal {A}_{m,n}: A\subseteq B_{m\ell }\} \leq R^{(n-m+1)\ell \delta (1-\varepsilon _1)}$
for any
$\#\{ A\in \mathcal {A}_{m,n}: A\subseteq B_{m\ell }\} \leq R^{(n-m+1)\ell \delta (1-\varepsilon _1)}$
for any
![]() $n\geq m\geq 0$
, by equations (16), (17), and (21), we get
$n\geq m\geq 0$
, by equations (16), (17), and (21), we get
 $$ \begin{align*} \varphi_{(i+1)\ell}(B_{(i+1)\ell}) & \leq \bigg(\frac{1}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}R^{-i\ell\delta(1-\varepsilon_2)}+\sum_{n=i+1}^{\infty}R^{(n-i)\ell\delta(1-\varepsilon_1)}R^{-(n+1)\ell\delta(1-\varepsilon_2)}\\ & = \bigg(\frac{R^{\delta(1-\varepsilon_2)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}R^{-(i+1)\ell\delta(1-\varepsilon_2)}+\sum_{n=1}^{\infty}R^{-n\ell\delta({\eta}/{2})}R^{-(i+1)\ell\delta(1-\varepsilon_2)}\\ & = \bigg(\bigg(\frac{R^{\delta(1-\varepsilon_2)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}+\frac{R^{-\ell\delta({\eta}/{2})}}{1-R^{-\ell\delta({\eta}/{2})}}\bigg)R^{-(i+1)\ell\delta(1-\varepsilon_2)}. \end{align*} $$
$$ \begin{align*} \varphi_{(i+1)\ell}(B_{(i+1)\ell}) & \leq \bigg(\frac{1}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}R^{-i\ell\delta(1-\varepsilon_2)}+\sum_{n=i+1}^{\infty}R^{(n-i)\ell\delta(1-\varepsilon_1)}R^{-(n+1)\ell\delta(1-\varepsilon_2)}\\ & = \bigg(\frac{R^{\delta(1-\varepsilon_2)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}R^{-(i+1)\ell\delta(1-\varepsilon_2)}+\sum_{n=1}^{\infty}R^{-n\ell\delta({\eta}/{2})}R^{-(i+1)\ell\delta(1-\varepsilon_2)}\\ & = \bigg(\bigg(\frac{R^{\delta(1-\varepsilon_2)}}{\lfloor R^{\delta(1-\varepsilon_0)}\rfloor+1}\bigg)^{\ell}+\frac{R^{-\ell\delta({\eta}/{2})}}{1-R^{-\ell\delta({\eta}/{2})}}\bigg)R^{-(i+1)\ell\delta(1-\varepsilon_2)}. \end{align*} $$
By equations (18) and (19), we get
which is what we need to complete the induction.
Theorem 3.2 can be rephrased in terms of local Cantor sets (cf. Example 2.8).
Corollary 3.3. Let
![]() $E\subseteq X$
. Let
$E\subseteq X$
. Let
![]() $B_0\subseteq X$
be a closed ball and
$B_0\subseteq X$
be a closed ball and
![]() $0<\varepsilon \leqslant 1$
. If E is
$0<\varepsilon \leqslant 1$
. If E is
![]() $\varepsilon $
Cantor winning on
$\varepsilon $
Cantor winning on
![]() $B_0$
, then for any
$B_0$
, then for any
![]() $R\geqslant 2$
, it contains a
$R\geqslant 2$
, it contains a
![]() $(B_0,R,f(R)^{1-\varepsilon })$
Cantor set.
$(B_0,R,f(R)^{1-\varepsilon })$
Cantor set.
Corollary 3.3 means that in Definition 2.10, it is enough to use local Cantor sets. This will be useful in the proof of Theorem 1.13.
For the sake of completeness, let us define a version of the Cantor game called the ‘Cantor potential game’. Its name is justified via the analogy with the potential game and the key role that potential functions, like the one in equation (20), play in the proof above that relates it to the Cantor game.
Given
![]() $\varepsilon _0\in (0,1]$
, the
$\varepsilon _0\in (0,1]$
, the
![]() $\varepsilon _0$
Cantor potential game is defined as follows: Bob starts by choosing
$\varepsilon _0$
Cantor potential game is defined as follows: Bob starts by choosing
![]() $0<\varepsilon <\varepsilon _0$
and Alice replies by choosing
$0<\varepsilon <\varepsilon _0$
and Alice replies by choosing
![]() $R_\varepsilon \geq 2$
. Then Bob chooses an integer
$R_\varepsilon \geq 2$
. Then Bob chooses an integer
![]() $R\geq R_\varepsilon $
and a closed ball
$R\geq R_\varepsilon $
and a closed ball
![]() $B_0\subseteq X$
. For any
$B_0\subseteq X$
. For any
![]() $i\geq 0$
, given Bob’s ith choice
$i\geq 0$
, given Bob’s ith choice
![]() $B_i$
, Alice chooses collections
$B_i$
, Alice chooses collections
![]() $\{\mathcal {A}_{i+1,k}\}_{k=0}^\infty $
such that
$\{\mathcal {A}_{i+1,k}\}_{k=0}^\infty $
such that
![]() $\mathcal {A}_{i+1,k}\subseteq {1}/{R}^k\{B_i\}$
and
$\mathcal {A}_{i+1,k}\subseteq {1}/{R}^k\{B_i\}$
and
for all
![]() $k\geq 0$
. Given
$k\geq 0$
. Given
![]() $\{\mathcal {A}_{i+1,k}\}_{k=0}^\infty $
, Bob chooses a ball
$\{\mathcal {A}_{i+1,k}\}_{k=0}^\infty $
, Bob chooses a ball
![]() $B_{i+1}\in {1}/{R}\{B_i\}\setminus \bigcup _{k=0}^{i}\mathcal {A}_{i+1-k,k}$
(if there is no such ball, we say that Alice wins by default). We say that
$B_{i+1}\in {1}/{R}\{B_i\}\setminus \bigcup _{k=0}^{i}\mathcal {A}_{i+1-k,k}$
(if there is no such ball, we say that Alice wins by default). We say that
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $\varepsilon $
Cantor potential winning if Alice has a strategy which guarantees that either she wins by default or equation (3) is satisfied. The Cantor potential game is defined by allowing Alice first to choose
$\varepsilon $
Cantor potential winning if Alice has a strategy which guarantees that either she wins by default or equation (3) is satisfied. The Cantor potential game is defined by allowing Alice first to choose
![]() $\varepsilon _0\in (0,1]$
and then continuing as in the
$\varepsilon _0\in (0,1]$
and then continuing as in the
![]() $\varepsilon _0$
Cantor potential game.
$\varepsilon _0$
Cantor potential game.
By definition,
![]() $\varepsilon _0$
Cantor winning is the same as
$\varepsilon _0$
Cantor winning is the same as
![]() $\varepsilon _0$
Cantor potential winning. Moreover, there is a natural way to pass between the collections that define a Cantor winning set to the winning strategy in the Cantor potential game. Indeed, if
$\varepsilon _0$
Cantor potential winning. Moreover, there is a natural way to pass between the collections that define a Cantor winning set to the winning strategy in the Cantor potential game. Indeed, if
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $\varepsilon _0$
Cantor winning in
$\varepsilon _0$
Cantor winning in
![]() $B_0$
given by the collections
$B_0$
given by the collections
![]() $\mathcal {B}_n$
and
$\mathcal {B}_n$
and
![]() $\mathcal {A}_{m,n}$
for any
$\mathcal {A}_{m,n}$
for any
![]() $n\geq 0$
and any
$n\geq 0$
and any
![]() $0\leq m\leq n$
, then a winning strategy for Alice for the
$0\leq m\leq n$
, then a winning strategy for Alice for the
![]() $\varepsilon _0$
Cantor potential game may be given by
$\varepsilon _0$
Cantor potential game may be given by
![]() $\mathcal {A}^{\prime }_{i+1,k} = \mathcal {A}_{i+1,k+i+1}(B_i)$
where
$\mathcal {A}^{\prime }_{i+1,k} = \mathcal {A}_{i+1,k+i+1}(B_i)$
where
![]() $B_i$
is Bob’s ith move. In the other direction, let
$B_i$
is Bob’s ith move. In the other direction, let
![]() $\mathcal {A}'$
denote a winning strategy for Alice for the
$\mathcal {A}'$
denote a winning strategy for Alice for the
![]() $\varepsilon _0$
Cantor potential game on
$\varepsilon _0$
Cantor potential game on
![]() $B_0$
for E, that is, if B is the ith move of Bob, denote by
$B_0$
for E, that is, if B is the ith move of Bob, denote by
![]() $\mathcal {A}^{\prime }_{i+1,k}(B_i)$
Alice’s
$\mathcal {A}^{\prime }_{i+1,k}(B_i)$
Alice’s
![]() $i+1$
st move according to this winning strategy. Define the collections
$i+1$
st move according to this winning strategy. Define the collections
![]() $\mathcal {B}_n$
for
$\mathcal {B}_n$
for
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\{\mathcal {A}_{m,n}\}_{0\leq m \leq n}$
for
$\{\mathcal {A}_{m,n}\}_{0\leq m \leq n}$
for
![]() $n\geq 1$
by recursion as follows:
$n\geq 1$
by recursion as follows:
![]() $\mathcal {B}_0=\{B_0\}$
,
$\mathcal {B}_0=\{B_0\}$
,
for every
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $0\leq m\leq n$
, and define
$0\leq m\leq n$
, and define
![]() $\mathcal {B}_n$
as usual via equation (10). Since
$\mathcal {B}_n$
as usual via equation (10). Since
![]() $\mathcal {A}'$
is a winning strategy, it implies that the limit set as in equation (11) is contained in E. Theorem 3.2 may then be reinterpreted as saying that the winning sets for the
$\mathcal {A}'$
is a winning strategy, it implies that the limit set as in equation (11) is contained in E. Theorem 3.2 may then be reinterpreted as saying that the winning sets for the
![]() $\varepsilon $
Cantor potential game are the same as the winning sets for the
$\varepsilon $
Cantor potential game are the same as the winning sets for the
![]() $\varepsilon $
Cantor game.
$\varepsilon $
Cantor game.
3.2. Cantor, absolute, and potential winning
We prove Theorem 1.5 as a special case of a more general result connecting potential winning sets with Cantor winning sets, corresponding to the standard splitting structure on
![]() $\mathbb {R}^N$
.
$\mathbb {R}^N$
.
Theorem 3.4. Let
![]() $(X,\mathcal {S},U,f)$
be a splitting structure on a doubling metric space X, fix
$(X,\mathcal {S},U,f)$
be a splitting structure on a doubling metric space X, fix
![]() $B_0\in \mathcal {B}(X)$
, and denote
$B_0\in \mathcal {B}(X)$
, and denote
Fix
![]() $\varepsilon _0 \in (0,1] $
and let
$\varepsilon _0 \in (0,1] $
and let
![]() $c_0 = \delta (1 - \varepsilon _0)$
. Then a set
$c_0 = \delta (1 - \varepsilon _0)$
. Then a set
![]() $E\subseteq A_\infty (B_0)$
is
$E\subseteq A_\infty (B_0)$
is
![]() $\varepsilon _0$
Cantor winning on
$\varepsilon _0$
Cantor winning on
![]() $B_0$
with respect to
$B_0$
with respect to
![]() $(X,\mathcal {S},U,f)$
if and only if E is
$(X,\mathcal {S},U,f)$
if and only if E is
![]() $c_0$
potential winning on
$c_0$
potential winning on
![]() $A_\infty (B_0)$
.
$A_\infty (B_0)$
.
In particular, E is Cantor winning on
![]() $B_0$
if and only if E is potential winning on
$B_0$
if and only if E is potential winning on
![]() $A_\infty (B_0)$
.
$A_\infty (B_0)$
.
Since potential winning is defined on metric spaces without using a splitting structure, we get the following observation.
Corollary 3.5. Cantor winning in a doubling metric space X is independent of the choice of splitting structure, provided that the limit set
![]() $A_\infty (B)$
is fixed.
$A_\infty (B)$
is fixed.
A combination of Proposition 1.3 and Theorem 3.4 yields the following corollary.
Corollary 3.6. Assume a complete metric space X is doubling and is endowed with a non-trivial splitting structure
![]() $(X,\mathcal {S},U,f)$
, and let
$(X,\mathcal {S},U,f)$
, and let
![]() $B_0 \in \mathcal {B}(X)$
. Then, a set
$B_0 \in \mathcal {B}(X)$
. Then, a set
![]() $E \subseteq X$
is
$E \subseteq X$
is
![]() $1$
Cantor winning on
$1$
Cantor winning on
![]() $B_0$
if and only if E is absolute winning on
$B_0$
if and only if E is absolute winning on
![]() $A_\infty (B_0)$
. In particular, for any splitting structure such that
$A_\infty (B_0)$
. In particular, for any splitting structure such that
![]() $B=A_\infty (B)$
for every ball B, a set
$B=A_\infty (B)$
for every ball B, a set
![]() $E \subseteq X$
is
$E \subseteq X$
is
![]() $1$
Cantor winning if and only if E is absolute winning.
$1$
Cantor winning if and only if E is absolute winning.
Remark 3.7. The statements in [Reference Badziahin and Harrap5, §7] immediately provide us with applications of Corollary 3.6. In particular, various sets from [Reference Badziahin and Harrap5, Theorems 14 and 15] are in fact absolutely winning.
We now prove Theorem 3.4.
Proof of forward direction
Since X is doubling, we may assume that
![]() $f(u) = u^{\delta }$
for every
$f(u) = u^{\delta }$
for every
![]() $u\in U$
(cf. [Reference Badziahin and Harrap5, Corollary 1]). Suppose that E is
$u\in U$
(cf. [Reference Badziahin and Harrap5, Corollary 1]). Suppose that E is
![]() $\varepsilon _0$
Cantor winning, and fix
$\varepsilon _0$
Cantor winning, and fix
![]() $\beta> 0$
,
$\beta> 0$
,
![]() $c> c_0$
, and
$c> c_0$
, and
![]() $\rho _0> 0$
. Fix
$\rho _0> 0$
. Fix
![]() $0 < \varepsilon < \varepsilon _0$
such that
$0 < \varepsilon < \varepsilon _0$
such that
![]() $\delta (1 - \varepsilon ) \in (c_0,c)$
. Fix large
$\delta (1 - \varepsilon ) \in (c_0,c)$
. Fix large
![]() $R\in U$
. Its precise value will be determined later. Potentially, R may depend on
$R\in U$
. Its precise value will be determined later. Potentially, R may depend on
![]() $\varepsilon $
,
$\varepsilon $
,
![]() $\beta $
, c, and
$\beta $
, c, and
![]() $\rho _0$
, and, in particular, it satisfies
$\rho _0$
, and, in particular, it satisfies
![]() $R \geq \max (R_\varepsilon ,1/\beta )$
and
$R \geq \max (R_\varepsilon ,1/\beta )$
and
![]() $R^{\delta (1-\varepsilon )-c}<\tfrac 12$
. Then by the definition of Cantor winning, E contains some
$R^{\delta (1-\varepsilon )-c}<\tfrac 12$
. Then by the definition of Cantor winning, E contains some
![]() $(B_0,R,\mathbf {r})$
Cantor set
$(B_0,R,\mathbf {r})$
Cantor set
![]() $\mathcal {K}$
, where
$\mathcal {K}$
, where
We now describe a strategy for Alice to win the
![]() $(c,\beta )$
potential game on
$(c,\beta )$
potential game on
![]() $A_\infty (B_0)$
, assuming that Bob’s starting move has radius
$A_\infty (B_0)$
, assuming that Bob’s starting move has radius
![]() $\rho _0$
. Recall that for any
$\rho _0$
. Recall that for any
![]() $B\in \mathcal {B}_m$
,
$B\in \mathcal {B}_m$
,
Let
![]() $\rho $
denote the radius of
$\rho $
denote the radius of
![]() $B_0$
, let
$B_0$
, let
![]() $D_k$
denote Bob’s kth move (we are denoting Bob’s kth move by
$D_k$
denote Bob’s kth move (we are denoting Bob’s kth move by
![]() $D_k$
instead of
$D_k$
instead of
![]() $B_m$
so as to reserve the letters B and m for the splitting structure framework), and for each
$B_m$
so as to reserve the letters B and m for the splitting structure framework), and for each
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $m = m_k\in \mathbb {N}$
denote the unique integer such that
$m = m_k\in \mathbb {N}$
denote the unique integer such that
![]() $\beta \cdot \mathrm {rad}(D_k) < R^{-m}\rho \leq \mathrm {rad}(D_k)$
, assuming such an integer exists. If such a number does not exist, then we say that
$\beta \cdot \mathrm {rad}(D_k) < R^{-m}\rho \leq \mathrm {rad}(D_k)$
, assuming such an integer exists. If such a number does not exist, then we say that
![]() $m_k$
is undefined. Then Alice’s strategy is as follows. On turn k, if
$m_k$
is undefined. Then Alice’s strategy is as follows. On turn k, if
![]() $m_k$
is defined, then remove all elements of the set
$m_k$
is defined, then remove all elements of the set
that intersect Bob’s current choice. If
![]() $m_k$
is undefined, then delete nothing. Obviously, this strategy, if executable, will make Alice win since the intersection of Bob’s balls will satisfy
$m_k$
is undefined, then delete nothing. Obviously, this strategy, if executable, will make Alice win since the intersection of Bob’s balls will satisfy
![]() $\bigcap _{k \in \mathbb {N}}D_k \subseteq \mathcal {K} \subseteq E$
. To show that it is legal, we need to show that
$\bigcap _{k \in \mathbb {N}}D_k \subseteq \mathcal {K} \subseteq E$
. To show that it is legal, we need to show that
 $$ \begin{align} \sum_{\substack{B\in \mathcal{B}_m \\ B\cap D_k \neq \varnothing}} \sum_{n \geq m} r_{m,n} (R^{-(n + 1)}\rho)^c \leq (\beta\cdot \mathrm{rad}(D_k))^c. \end{align} $$
$$ \begin{align} \sum_{\substack{B\in \mathcal{B}_m \\ B\cap D_k \neq \varnothing}} \sum_{n \geq m} r_{m,n} (R^{-(n + 1)}\rho)^c \leq (\beta\cdot \mathrm{rad}(D_k))^c. \end{align} $$
This is because elements of
![]() $\mathcal {A}_{m,n}(B)$
all have radius
$\mathcal {A}_{m,n}(B)$
all have radius
![]() $R^{-(n + 1)}\rho $
.
$R^{-(n + 1)}\rho $
.
To estimate the sum in question, we use the fact that X is doubling. Since the elements of
![]() $\mathcal {B}_m$
have disjoint interiors and have radius
$\mathcal {B}_m$
have disjoint interiors and have radius
![]() $R^{-m} \rho \asymp _\beta \mathrm {rad}(D_k)$
, the number of them that intersect
$R^{-m} \rho \asymp _\beta \mathrm {rad}(D_k)$
, the number of them that intersect
![]() $D_k$
is bounded by a constant depending only on
$D_k$
is bounded by a constant depending only on
![]() $\beta $
. Call this constant
$\beta $
. Call this constant
![]() $C_1$
. Then the left-hand side of equation (24) is less than
$C_1$
. Then the left-hand side of equation (24) is less than
 $$ \begin{align*} &C_1 \sum_{n\geq m} R^{\delta(n - m + 1)(1 - \varepsilon)} (R^{-(n + 1)}\rho)^c\\ &\quad= C_1 (R^{-m} \rho)^c \sum_{\ell = 1}^\infty R^{\delta(1 - \varepsilon)\ell} R^{-c\ell}\\ &\quad\leqslant 2 C_1 (\mathrm{rad}(D_k))^c R^{\delta(1 - \varepsilon) - c} \quad\big(\text{since }R^{\delta(1 - \varepsilon) - c}\leqslant \tfrac12\big). \end{align*} $$
$$ \begin{align*} &C_1 \sum_{n\geq m} R^{\delta(n - m + 1)(1 - \varepsilon)} (R^{-(n + 1)}\rho)^c\\ &\quad= C_1 (R^{-m} \rho)^c \sum_{\ell = 1}^\infty R^{\delta(1 - \varepsilon)\ell} R^{-c\ell}\\ &\quad\leqslant 2 C_1 (\mathrm{rad}(D_k))^c R^{\delta(1 - \varepsilon) - c} \quad\big(\text{since }R^{\delta(1 - \varepsilon) - c}\leqslant \tfrac12\big). \end{align*} $$
By choosing R large enough so that
we guarantee that the move is legal.
Proof of backward direction
Suppose that
![]() $E \subseteq A_\infty (B_0)$
is
$E \subseteq A_\infty (B_0)$
is
![]() $c_0$
potential winning and fix
$c_0$
potential winning and fix
![]() $0 < \varepsilon < \varepsilon _0$
. Let
$0 < \varepsilon < \varepsilon _0$
. Let
![]() $R_\varepsilon = 2$
and fix
$R_\varepsilon = 2$
and fix
![]() $R\in U$
such that
$R\in U$
such that
![]() $R\geq R_\varepsilon $
. Fix a large integer
$R\geq R_\varepsilon $
. Fix a large integer
![]() $q\in \mathbb {N}$
to be determined, and let
$q\in \mathbb {N}$
to be determined, and let
![]() $\beta = 1/R^q$
and
$\beta = 1/R^q$
and
![]() $c = \delta (1 - \varepsilon )$
. Then E is
$c = \delta (1 - \varepsilon )$
. Then E is
![]() $(c,\beta )$
potential winning. Now for each
$(c,\beta )$
potential winning. Now for each
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $B\in \mathcal {B}_{qk}$
, let
$B\in \mathcal {B}_{qk}$
, let
![]() $\mathcal {A}(B)$
denote the collection of sets that Alice deletes in response to Bob’s kth move
$\mathcal {A}(B)$
denote the collection of sets that Alice deletes in response to Bob’s kth move
![]() $B_k=B$
, assuming that it has been preceded by the moves
$B_k=B$
, assuming that it has been preceded by the moves
![]() $B_0,B_1,\ldots ,B_{k-1}$
satisfying
$B_0,B_1,\ldots ,B_{k-1}$
satisfying
![]() $B_{i + 1}\in \mathcal {S}(B_i,R^q)$
for all
$B_{i + 1}\in \mathcal {S}(B_i,R^q)$
for all
![]() $i = 0,\ldots ,k - 1$
. (It is necessary to specify the history to uniquely identify Alice’s response because unlike the other variants of Schmidt’s game, the potential game is not a positional game (see §3.4 and [Reference Schmidt37, Theorem 7]). This is because the regions that were deleted at previous stages of the game affect the overall situation and therefore may affect Alice’s strategy.) Since Alice’s strategy is winning, we must have
$i = 0,\ldots ,k - 1$
. (It is necessary to specify the history to uniquely identify Alice’s response because unlike the other variants of Schmidt’s game, the potential game is not a positional game (see §3.4 and [Reference Schmidt37, Theorem 7]). This is because the regions that were deleted at previous stages of the game affect the overall situation and therefore may affect Alice’s strategy.) Since Alice’s strategy is winning, we must have
 $$ \begin{align*} E\supseteq A_\infty(B_0) \setminus \bigcup_{k\in\mathbb{N}} \bigcup_{B\in \mathcal{B}_{qk}} \bigcup_{A\in \mathcal{A}(B)} A. \end{align*} $$
$$ \begin{align*} E\supseteq A_\infty(B_0) \setminus \bigcup_{k\in\mathbb{N}} \bigcup_{B\in \mathcal{B}_{qk}} \bigcup_{A\in \mathcal{A}(B)} A. \end{align*} $$
Indeed, for every point on the right-hand side, there is some strategy that Bob can use to force the outcome to equal that point (and also not lose by default). So to complete the proof, it suffices to show that the right-hand side contains a
![]() $(B_0,R,\mathbf {r})$
Cantor set, where
$(B_0,R,\mathbf {r})$
Cantor set, where
For each
![]() $m = qk \leq n$
and
$m = qk \leq n$
and
![]() $B\in \mathcal {B}_m$
, let
$B\in \mathcal {B}_m$
, let
![]() $\mathcal {C}(n)$
be the collection of elements of
$\mathcal {C}(n)$
be the collection of elements of
![]() $\mathcal {A}(B)$
whose radius is between
$\mathcal {A}(B)$
whose radius is between
![]() $R^{-n}\rho $
and
$R^{-n}\rho $
and
![]() $R^{-(n + 1)}\rho $
, where
$R^{-(n + 1)}\rho $
, where
![]() $\rho $
is the radius of
$\rho $
is the radius of
![]() $B_0$
. Define
$B_0$
. Define
By equation (7) and the definition of
![]() $\mathcal {C}(n)$
, we have
$\mathcal {C}(n)$
, we have
 $$ \begin{align*} \sum_{C\in\mathcal{C}(n)} (R^{-(n+1)}\rho)^c \leq (\beta R^{-m}\rho)^c; \end{align*} $$
$$ \begin{align*} \sum_{C\in\mathcal{C}(n)} (R^{-(n+1)}\rho)^c \leq (\beta R^{-m}\rho)^c; \end{align*} $$
that is,
This implies that for
![]() $m>n$
, we get
$m>n$
, we get
![]() $\#\mathcal {C}(n)<1$
, that is,
$\#\mathcal {C}(n)<1$
, that is,
![]() $\mathcal {C}(n) = \emptyset $
and, in turn,
$\mathcal {C}(n) = \emptyset $
and, in turn,
![]() $\mathcal {A}_{m,n} (B) = \emptyset $
. Now we construct a Cantor set
$\mathcal {A}_{m,n} (B) = \emptyset $
. Now we construct a Cantor set
![]() $\mathcal {K}\in E$
by removing the collections
$\mathcal {K}\in E$
by removing the collections
![]() $\mathcal {A}_{m,n}(B)$
(
$\mathcal {A}_{m,n}(B)$
(
![]() $m\leq n$
,
$m\leq n$
,
![]() $B\in \mathcal {B}_m$
). Then to complete the proof, we just need to show that
$B\in \mathcal {B}_m$
). Then to complete the proof, we just need to show that
for every
![]() $B\in \mathcal {B}_m$
. By the doubling property, each element of
$B\in \mathcal {B}_m$
. By the doubling property, each element of
![]() $\mathcal {C}(n)$
intersects a bounded number of elements of
$\mathcal {C}(n)$
intersects a bounded number of elements of
![]() $\mathcal {S}(B,R^{n - m + 1})$
. Thus,
$\mathcal {S}(B,R^{n - m + 1})$
. Thus,
for some constant
![]() $C_3> 0$
depending on R. By letting
$C_3> 0$
depending on R. By letting
![]() $\beta $
be sufficiently small (that is, letting q be sufficiently large), we can get
$\beta $
be sufficiently small (that is, letting q be sufficiently large), we can get
![]() $C_3 \beta ^c \leq 1$
and therefore
$C_3 \beta ^c \leq 1$
and therefore
which completes the proof.
Finally, we briefly mention how the second statement of Theorem 1.5 follows from the first statement. If E is 1 Cantor winning then, by the first part of the theorem, it is c potential winning for any
![]() $c>0$
. The statement follows as an immediate corollary of Proposition 1.3.
$c>0$
. The statement follows as an immediate corollary of Proposition 1.3.
3.3. Schmidt’s winning and Cantor winning
We now move our attention to the links between Schmidt’s original game and generalized Cantor set constructions. Thanks to Theorem 3.4, in
![]() $\delta $
Ahlfors regular spaces, we can treat the notions of Cantor winning sets and potential winning sets as interchangeable. The latter notion will be more convenient in this section. We prove Theorem 1.9 as a special case of a more general result.
$\delta $
Ahlfors regular spaces, we can treat the notions of Cantor winning sets and potential winning sets as interchangeable. The latter notion will be more convenient in this section. We prove Theorem 1.9 as a special case of a more general result.
Theorem 3.8. Let X be a
![]() $\delta $
Ahlfors regular space and let
$\delta $
Ahlfors regular space and let
![]() $E\subseteq X$
be a
$E\subseteq X$
be a
![]() $c_0$
potential winning set. Then for all
$c_0$
potential winning set. Then for all
![]() $c> c_0$
, there exists
$c> c_0$
, there exists
![]() $\gamma> 0$
such that for all
$\gamma> 0$
such that for all
![]() $\alpha ,\beta> 0$
with
$\alpha ,\beta> 0$
with
![]() $\alpha < \gamma (\alpha \beta )^{c/\delta }$
, the set E is
$\alpha < \gamma (\alpha \beta )^{c/\delta }$
, the set E is
![]() $(\alpha ,\beta )$
very strong winning.
$(\alpha ,\beta )$
very strong winning.
To see that Theorem 1.9 follows from Theorem 3.8, notice that
![]() $\mathbb {R}^N$
is N Ahlfors regular, and that very strong
$\mathbb {R}^N$
is N Ahlfors regular, and that very strong
![]() $(\alpha ,\beta )$
winning sets are
$(\alpha ,\beta )$
winning sets are
![]() $(\alpha ,\beta )$
winning. When E is
$(\alpha ,\beta )$
winning. When E is
![]() $\varepsilon $
Cantor winning, the desired statement follows upon taking
$\varepsilon $
Cantor winning, the desired statement follows upon taking
![]() $c_0=N(1-\varepsilon )$
in the above. The reader may wish to compare the following proof with the proof of Theorem 3.2.
$c_0=N(1-\varepsilon )$
in the above. The reader may wish to compare the following proof with the proof of Theorem 3.2.
Proof. Consider a strategy for Alice to win the
![]() $(c,\widetilde \beta )$
potential game for the set E, where
$(c,\widetilde \beta )$
potential game for the set E, where
![]() $\widetilde \beta = (\alpha \beta )^q$
for some large
$\widetilde \beta = (\alpha \beta )^q$
for some large
![]() $q\in \mathbb {N}$
. We want to show that Alice has a winning strategy in the
$q\in \mathbb {N}$
. We want to show that Alice has a winning strategy in the
![]() $(\alpha ,\beta )$
very strong game. Given any sequence of Bob’s choices in the
$(\alpha ,\beta )$
very strong game. Given any sequence of Bob’s choices in the
![]() $(\alpha ,\beta )$
game, say
$(\alpha ,\beta )$
game, say
![]() $B_0,\ldots ,B_{qk}$
, we can consider the corresponding sequence of choices in the
$B_0,\ldots ,B_{qk}$
, we can consider the corresponding sequence of choices in the
![]() $(c,\widetilde \beta )$
potential game which correspond to Bob choosing the balls
$(c,\widetilde \beta )$
potential game which correspond to Bob choosing the balls
![]() $B_0,B_q,\ldots ,B_{qk}$
. Alice’s response to this sequence of moves is to delete a collection
$B_0,B_q,\ldots ,B_{qk}$
. Alice’s response to this sequence of moves is to delete a collection
![]() $\mathcal {A}(B_{qk})$
. Now Alice’s corresponding response in the
$\mathcal {A}(B_{qk})$
. Now Alice’s corresponding response in the
![]() $(\alpha ,\beta )$
very strong game will be: if Bob has made the sequence of moves
$(\alpha ,\beta )$
very strong game will be: if Bob has made the sequence of moves
![]() $B_0,\ldots ,B_m$
, then she will choose her ball
$B_0,\ldots ,B_m$
, then she will choose her ball
![]() $A_{m+1} \subseteq B_m$
so as to minimize the value at
$A_{m+1} \subseteq B_m$
so as to minimize the value at
![]() $A_{m+1}$
of the potential function
$A_{m+1}$
of the potential function
 $$ \begin{align*} \varphi_m(A) := \sum_{\substack{k\in\mathbb{N} \\ qk \leq m}} \sum_{\substack{C\in\mathcal{A}(B_{qk}) \\ C\cap A \neq \varnothing}} \mathrm{diam}^c(C). \end{align*} $$
$$ \begin{align*} \varphi_m(A) := \sum_{\substack{k\in\mathbb{N} \\ qk \leq m}} \sum_{\substack{C\in\mathcal{A}(B_{qk}) \\ C\cap A \neq \varnothing}} \mathrm{diam}^c(C). \end{align*} $$
We will now prove by induction that the inequality
holds for all m, where
![]() $\varepsilon> 0$
will be chosen later (small but independent of
$\varepsilon> 0$
will be chosen later (small but independent of
![]() $\widetilde \beta $
). Suppose that it holds for some m and let
$\widetilde \beta $
). Suppose that it holds for some m and let
![]() $B_{m + 1}$
be Bob’s next move. Define
$B_{m + 1}$
be Bob’s next move. Define
![]() $r = \alpha \cdot \mathrm {rad}(B_{m+1})\geqslant \alpha ^2\beta \cdot \mathrm {rad}(B_m)$
. By Proposition 2.19, there exists a set
$r = \alpha \cdot \mathrm {rad}(B_{m+1})\geqslant \alpha ^2\beta \cdot \mathrm {rad}(B_m)$
. By Proposition 2.19, there exists a set
which satisfies the following conditions:
![]() $I = \#\mathcal {D} \gg \alpha ^{-\delta }$
, and for any distinct values
$I = \#\mathcal {D} \gg \alpha ^{-\delta }$
, and for any distinct values
![]() $1\leqslant i\neq j\leqslant I$
, one has
$1\leqslant i\neq j\leqslant I$
, one has
![]() $d(x_i,x_j)\geqslant 3r$
, i.e. all balls in
$d(x_i,x_j)\geqslant 3r$
, i.e. all balls in
![]() $\mathcal {D}$
are separated by distances of at least r.
$\mathcal {D}$
are separated by distances of at least r.
By the induction hypothesis, for all
![]() $C\in \bigcup _{qk\leq m} \mathcal {A}(B_{qk})$
such that
$C\in \bigcup _{qk\leq m} \mathcal {A}(B_{qk})$
such that
![]() $C\cap A_{m+1} \neq \emptyset $
, we have
$C\cap A_{m+1} \neq \emptyset $
, we have
![]() $\mathrm {diam}(C) \leq \varepsilon \cdot \mathrm {rad}(B_m)$
. So by letting
$\mathrm {diam}(C) \leq \varepsilon \cdot \mathrm {rad}(B_m)$
. So by letting
![]() $\varepsilon $
be small enough (that is,
$\varepsilon $
be small enough (that is,
![]() $\varepsilon \leq \alpha ^2\beta $
), we can guarantee that all balls in
$\varepsilon \leq \alpha ^2\beta $
), we can guarantee that all balls in
![]() $\mathcal {D}$
make disjoint contributions to
$\mathcal {D}$
make disjoint contributions to
![]() $\varphi _m(A_{m+1})$
. In other words,
$\varphi _m(A_{m+1})$
. In other words,
By choosing
![]() $A_{m + 2}$
to be the ball from
$A_{m + 2}$
to be the ball from
![]() $\mathcal {D}$
which minimizes the function
$\mathcal {D}$
which minimizes the function
![]() $\varphi _m$
, we get
$\varphi _m$
, we get
By choosing
![]() $\gamma $
small enough, the inequality
$\gamma $
small enough, the inequality
![]() $\alpha < \gamma (\alpha \beta )^{c/\delta }$
implies that
$\alpha < \gamma (\alpha \beta )^{c/\delta }$
implies that
Note that for the base of induction,
![]() $m=-1$
, the last estimate is straightforward, since
$m=-1$
, the last estimate is straightforward, since
![]() $\varphi _m(A) = 0$
for all balls A, and we can set
$\varphi _m(A) = 0$
for all balls A, and we can set
![]() $A_0=B_0$
.
$A_0=B_0$
.
When we consider
![]() $\varphi _{m+1}(A_{m+2})$
, there may be a new term coming from a new collection
$\varphi _{m+1}(A_{m+2})$
, there may be a new term coming from a new collection
![]() $\mathcal {A}(B_{m + 1})$
. By the definition of a
$\mathcal {A}(B_{m + 1})$
. By the definition of a
![]() $(c,\widetilde \beta )$
potential game, that term is at most
$(c,\widetilde \beta )$
potential game, that term is at most
![]() $(\widetilde \beta \cdot \mathrm {rad}(B_{m+1}))^c$
, and thus by choosing q large enough, we can guarantee that
$(\widetilde \beta \cdot \mathrm {rad}(B_{m+1}))^c$
, and thus by choosing q large enough, we can guarantee that
This finishes the induction.
Since Alice followed the winning strategy for
![]() $(c,\widetilde \beta )$
potential game, we have either
$(c,\widetilde \beta )$
potential game, we have either
 $$ \begin{align*} \bigcap_{k=1}^\infty B_{kq} \subseteq E\quad\text{or}\quad \bigcap_{k=1}^\infty B_{kq} \subseteq \bigcup_{k=1}^\infty \bigcup_{A\in\mathcal{A}(B_{kq})} A. \end{align*} $$
$$ \begin{align*} \bigcap_{k=1}^\infty B_{kq} \subseteq E\quad\text{or}\quad \bigcap_{k=1}^\infty B_{kq} \subseteq \bigcup_{k=1}^\infty \bigcup_{A\in\mathcal{A}(B_{kq})} A. \end{align*} $$
To finish the proof of the theorem, we need to show that the second inclusion is impossible. If we assume the contrary, then there exists
![]() $A\in \mathcal {A}(B_{kq})$
for some k such that every ball
$A\in \mathcal {A}(B_{kq})$
for some k such that every ball
![]() $B_m$
and, in turn, every ball
$B_m$
and, in turn, every ball
![]() $A_m$
has non-empty intersection with A. However, in that case, we have
$A_m$
has non-empty intersection with A. However, in that case, we have
![]() $\varphi _m(A_{m+1}) \geq \mathrm {diam}^c(A)$
, which contradicts the fact that
$\varphi _m(A_{m+1}) \geq \mathrm {diam}^c(A)$
, which contradicts the fact that
![]() $\varphi _m(A_{m+1}) \to 0$
as
$\varphi _m(A_{m+1}) \to 0$
as
![]() $m\to \infty $
.
$m\to \infty $
.
As a corollary of Theorem 3.8, we get a general form of Theorem 1.10.
Corollary 3.9. In an Ahlfors regular space, the intersection of a weak winning set and a potential winning set has full Hausdorff dimension.
Proof. Let
![]() $E\subseteq X$
be a
$E\subseteq X$
be a
![]() $c_0$
potential winning set for some
$c_0$
potential winning set for some
![]() $c_0<\delta $
. Fix
$c_0<\delta $
. Fix
![]() $c_0 < c < \delta $
. By Theorem 3.8, there exists
$c_0 < c < \delta $
. By Theorem 3.8, there exists
![]() $\gamma> 0$
such that for all
$\gamma> 0$
such that for all
![]() $\alpha ,\beta>0$
with
$\alpha ,\beta>0$
with
![]() $\alpha < \gamma (\alpha \beta )^{c/\delta }$
, E is
$\alpha < \gamma (\alpha \beta )^{c/\delta }$
, E is
![]() $(\alpha ,\beta )$
very strong winning. In particular, for all
$(\alpha ,\beta )$
very strong winning. In particular, for all
![]() $\beta> 0$
, there exists
$\beta> 0$
, there exists
![]() $\alpha> 0$
such that E is
$\alpha> 0$
such that E is
![]() $(\alpha ,\beta )$
very strong winning. Hence, we can apply Proposition 2.6 which says that
$(\alpha ,\beta )$
very strong winning. Hence, we can apply Proposition 2.6 which says that
![]() $X\setminus E$
is not weak winning (and thus does not contain a weak winning set). So every potential winning set intersects every weak winning set non-trivially.
$X\setminus E$
is not weak winning (and thus does not contain a weak winning set). So every potential winning set intersects every weak winning set non-trivially.
Now by contradiction, suppose that T is a weak winning set such that
![]() ${\dim _H}(E\cap T) < \delta $
. This implies that for any
${\dim _H}(E\cap T) < \delta $
. This implies that for any
![]() $c \in ({\dim _H}(E\cap T), \delta )$
and for any
$c \in ({\dim _H}(E\cap T), \delta )$
and for any
![]() $\varepsilon>0$
, one can construct a cover of
$\varepsilon>0$
, one can construct a cover of
![]() $E\cap T$
by a countable collection
$E\cap T$
by a countable collection
![]() $(A_i)_{i\in \mathbb {N}}$
of balls such that
$(A_i)_{i\in \mathbb {N}}$
of balls such that
 $$ \begin{align*} \sum_{i=1}^\infty \mathrm{diam}^c(A_i) <\varepsilon. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^\infty \mathrm{diam}^c(A_i) <\varepsilon. \end{align*} $$
In other words, this cover can be chosen by Alice in a single move of the c potential game, so
![]() $X\setminus (E\cap T)$
is potential winning. So by the intersection property of potential winning sets,
$X\setminus (E\cap T)$
is potential winning. So by the intersection property of potential winning sets,
![]() $E\setminus T = E\cap (X\setminus (E\cap T))$
is potential winning. However, then
$E\setminus T = E\cap (X\setminus (E\cap T))$
is potential winning. However, then
![]() $X\setminus T$
is a potential winning set whose complement is weak winning, contradicting what we have just shown.
$X\setminus T$
is a potential winning set whose complement is weak winning, contradicting what we have just shown.
3.4. Proof of Theorem 1.11
In this section, we prove that
![]() $1/2$
winning implies absolute winning for subsets of the real line. The same notation, terminology, and observations as in [Reference Schmidt37] are employed. Recall that
$1/2$
winning implies absolute winning for subsets of the real line. The same notation, terminology, and observations as in [Reference Schmidt37] are employed. Recall that
![]() $\mathcal {B}(\mathbb {R})$
stands for the set of all closed intervals in
$\mathcal {B}(\mathbb {R})$
stands for the set of all closed intervals in
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
In Schmidt’s
![]() $(\alpha , \beta )$
game, the method Alice uses to determine where to play her intervals
$(\alpha , \beta )$
game, the method Alice uses to determine where to play her intervals
![]() $A_i$
is called a strategy. Formally, a strategy
$A_i$
is called a strategy. Formally, a strategy
![]() $F:=\{f_1, f_2, \ldots \}$
is a sequence of functions
$F:=\{f_1, f_2, \ldots \}$
is a sequence of functions
![]() $f_i: \mathcal {B}(\mathbb {R})^i \rightarrow \mathcal {B}(\mathbb {R})$
satisfying
$f_i: \mathcal {B}(\mathbb {R})^i \rightarrow \mathcal {B}(\mathbb {R})$
satisfying
![]() $\mathrm {rad}(f_i(B_0, B_1, \ldots , B_{i-1})) = \alpha \cdot \mathrm {rad}(B_{i-1})$
and
$\mathrm {rad}(f_i(B_0, B_1, \ldots , B_{i-1})) = \alpha \cdot \mathrm {rad}(B_{i-1})$
and
![]() $f_i(B_0, B_1, \ldots , B_{i-1}) \subseteq B_{i-1}$
. A set E is a winning set for the
$f_i(B_0, B_1, \ldots , B_{i-1}) \subseteq B_{i-1}$
. A set E is a winning set for the
![]() $(\alpha , \beta )$
game if and only if there exists a strategy determining where Alice should place her intervals
$(\alpha , \beta )$
game if and only if there exists a strategy determining where Alice should place her intervals
![]() $A_{i}:=f_i(B_0, B_1, \ldots , B_{i-1})$
, so that however Bob chooses his intervals
$A_{i}:=f_i(B_0, B_1, \ldots , B_{i-1})$
, so that however Bob chooses his intervals
![]() $B_{i} \subseteq A_{i}$
, the intersection point
$B_{i} \subseteq A_{i}$
, the intersection point
![]() $\bigcap _{i} B_i$
lies in E. Such a strategy is referred to as a winning strategy (for E). Schmidt [Reference Schmidt37, Theorem
$\bigcap _{i} B_i$
lies in E. Such a strategy is referred to as a winning strategy (for E). Schmidt [Reference Schmidt37, Theorem
![]() $7$
] observed that the existence of a winning strategy guarantees the existence of a positional winning strategy; that is, a winning strategy for which the placement of a given interval by Alice needs only to depend upon the position of Bob’s immediately preceding interval, not on the entirety of the game so far. To be precise, a winning strategy
$7$
] observed that the existence of a winning strategy guarantees the existence of a positional winning strategy; that is, a winning strategy for which the placement of a given interval by Alice needs only to depend upon the position of Bob’s immediately preceding interval, not on the entirety of the game so far. To be precise, a winning strategy
![]() $F:=(f_1, f_2, \ldots )$
is positional if there is a function
$F:=(f_1, f_2, \ldots )$
is positional if there is a function
![]() $f_0: \mathcal {B}(X) \rightarrow \mathcal {B}(\mathbb {R})$
such that each function
$f_0: \mathcal {B}(X) \rightarrow \mathcal {B}(\mathbb {R})$
such that each function
![]() $f_i \in F$
satisfies
$f_i \in F$
satisfies
![]() $f_i(B_0, \ldots , B_{i-1})=f_0(B_{i-1})$
. Employing a positional strategy will not give us any real advantage in the proof that follows; however, it will allow us to simplify our notation somewhat. Without confusion, we will write
$f_i(B_0, \ldots , B_{i-1})=f_0(B_{i-1})$
. Employing a positional strategy will not give us any real advantage in the proof that follows; however, it will allow us to simplify our notation somewhat. Without confusion, we will write
![]() $A_i=F(B_{i-1}) = f_0(B_{i-1})$
where F is a given positional winning strategy for Alice and
$A_i=F(B_{i-1}) = f_0(B_{i-1})$
where F is a given positional winning strategy for Alice and
![]() $f_0$
is the function witnessing F’s positionality.
$f_0$
is the function witnessing F’s positionality.
We refer to a sequence
![]() $\{B_0, B_1, \ldots \}$
of intervals as an F-chain if it consists of the moves Bob has made during the playing out of an
$\{B_0, B_1, \ldots \}$
of intervals as an F-chain if it consists of the moves Bob has made during the playing out of an
![]() $(\alpha , \beta )$
game with target set E in which Alice has followed the winning strategy F. By definition, we must have
$(\alpha , \beta )$
game with target set E in which Alice has followed the winning strategy F. By definition, we must have
![]() $\bigcap _{i} B_i \, \subseteq E$
. Furthermore, we say a finite sequence
$\bigcap _{i} B_i \, \subseteq E$
. Furthermore, we say a finite sequence
![]() $\{B_0, \ldots B_{n-1}\}$
is an
$\{B_0, \ldots B_{n-1}\}$
is an
![]() $F_n$
-chain if there exist
$F_n$
-chain if there exist
![]() $B_{n}, B_{n+1}, \ldots $
for which the infinite sequence
$B_{n}, B_{n+1}, \ldots $
for which the infinite sequence
![]() $\{B_0, \ldots B_{n-1}, B_{n}, B_{n+1} \ldots \}$
is an F-chain. One can readily verify (see [Reference Schmidt37, Lemma
$\{B_0, \ldots B_{n-1}, B_{n}, B_{n+1} \ldots \}$
is an F-chain. One can readily verify (see [Reference Schmidt37, Lemma
![]() $1$
]) that if
$1$
]) that if
![]() $\{B_0, B_1, \ldots \}$
is a sequence of intervals such that for every
$\{B_0, B_1, \ldots \}$
is a sequence of intervals such that for every
![]() $n \in \mathbb {N}$
, the finite sequence
$n \in \mathbb {N}$
, the finite sequence
![]() $\{B_0, B_1, \ldots B_{n-1}\}$
is an
$\{B_0, B_1, \ldots B_{n-1}\}$
is an
![]() $F_n$
-chain, then
$F_n$
-chain, then
![]() $\{B_0, B_1, \ldots \}$
is an F-chain.
$\{B_0, B_1, \ldots \}$
is an F-chain.
Outline of the strategy. We begin with some interval
![]() $b_0 \subseteq \mathbb {R}$
of length
$b_0 \subseteq \mathbb {R}$
of length
![]() $2\cdot \mathrm {rad}(b_0)$
, some
$2\cdot \mathrm {rad}(b_0)$
, some
![]() $\varepsilon \in (0, 1)$
, some R sufficiently large, and a
$\varepsilon \in (0, 1)$
, some R sufficiently large, and a
![]() $1/2$
winning set
$1/2$
winning set
![]() $E \subseteq \mathbb {R}$
. Fix
$E \subseteq \mathbb {R}$
. Fix
![]() $\alpha =1/2$
and
$\alpha =1/2$
and
![]() $\beta =2/R$
, so that
$\beta =2/R$
, so that
![]() $\alpha \beta = 1/R$
. We will construct for every
$\alpha \beta = 1/R$
. We will construct for every
![]() $R \geq 10^{1/(1-\varepsilon )}$
, a local
$R \geq 10^{1/(1-\varepsilon )}$
, a local
![]() $(b_0, R, 10)$
Cantor set
$(b_0, R, 10)$
Cantor set
![]() $\mathcal {K}$
lying inside E. This is sufficient to prove that E is
$\mathcal {K}$
lying inside E. This is sufficient to prove that E is
![]() $1$
Cantor winning.
$1$
Cantor winning.
By assumption, the set E is
![]() $(1/2, 2/R)$
winning; thus, there exists a positional winning strategy F such that however we choose to place Bob’s intervals
$(1/2, 2/R)$
winning; thus, there exists a positional winning strategy F such that however we choose to place Bob’s intervals
![]() $B_i$
in the game, the placement of Alice’s subsequent intervals
$B_i$
in the game, the placement of Alice’s subsequent intervals
![]() $A_i=F(B_{i-1})$
guarantees that the unique element of
$A_i=F(B_{i-1})$
guarantees that the unique element of
![]() $\bigcap _i B_i$
will fall inside E. We will, in a sense, play as Bob in many simultaneous
$\bigcap _i B_i$
will fall inside E. We will, in a sense, play as Bob in many simultaneous
![]() $(1/2, 2/R)$
games, each of which Alice will win by following her prescribed strategy F.
$(1/2, 2/R)$
games, each of which Alice will win by following her prescribed strategy F.
Our procedure is as follows. The construction of the local Cantor set
![]() $\mathcal {K}$
comprises the construction of subcollections
$\mathcal {K}$
comprises the construction of subcollections
![]() $\mathcal {B}_n$
of intervals in
$\mathcal {B}_n$
of intervals in
![]() $1/{R}^n \mathcal {B}_0$
for each
$1/{R}^n \mathcal {B}_0$
for each
![]() $n \in \mathbb {N}$
, where
$n \in \mathbb {N}$
, where
![]() $\mathcal {B}_0:=\{ b_0\}$
. Construction will be carried out iteratively in such a way that for any interval
$\mathcal {B}_0:=\{ b_0\}$
. Construction will be carried out iteratively in such a way that for any interval
![]() $b \in \mathcal {B}_n$
, there exists an
$b \in \mathcal {B}_n$
, there exists an
![]() $F_n$
-chain
$F_n$
-chain
![]() $\{B_0, B_1, \ldots , B_{n-1}\}$
satisfying
$\{B_0, B_1, \ldots , B_{n-1}\}$
satisfying
![]() $b \subseteq B_{n-1}$
. Moreover, for each ancestor
$b \subseteq B_{n-1}$
. Moreover, for each ancestor
![]() $b'$
of b (that is, the unique interval
$b'$
of b (that is, the unique interval
![]() $b' \in \mathcal {B}_k$
with
$b' \in \mathcal {B}_k$
with
![]() $b \subseteq b'$
, for some given
$b \subseteq b'$
, for some given
![]() $0 \leq k < n$
), the subsequence
$0 \leq k < n$
), the subsequence
![]() $\{B_0, B_1, \ldots , B_{k-1}\} $
will coincide with the
$\{B_0, B_1, \ldots , B_{k-1}\} $
will coincide with the
![]() $F_k$
-chain constructed for
$F_k$
-chain constructed for
![]() $b'$
satisfying
$b'$
satisfying
![]() $b' \subseteq B_{k-1}$
from the earlier inductive steps. We write
$b' \subseteq B_{k-1}$
from the earlier inductive steps. We write
![]() $B_n(b)$
if the dependence of the interval
$B_n(b)$
if the dependence of the interval
![]() $B_n$
on an interval b is not clear from context. In view of the previous discussion, upon completion of the iterative procedure, it follows that for any sequence of intervals
$B_n$
on an interval b is not clear from context. In view of the previous discussion, upon completion of the iterative procedure, it follows that for any sequence of intervals
![]() $\{b_i\}_{i \in \mathbb {N}}$
with
$\{b_i\}_{i \in \mathbb {N}}$
with
![]() $b_i \in \mathcal {B}_i$
, the associated sequence
$b_i \in \mathcal {B}_i$
, the associated sequence
![]() $\{B_0, B_1, \ldots \}$
must be an F-chain satisfying
$\{B_0, B_1, \ldots \}$
must be an F-chain satisfying
![]() $b_i \subseteq B_{i-1}$
. In this way, for every point
$b_i \subseteq B_{i-1}$
. In this way, for every point
![]() $\mathbf {x}$
in the Cantor set
$\mathbf {x}$
in the Cantor set
![]() $\mathcal {K}$
, we will establish the existence of an F-chain
$\mathcal {K}$
, we will establish the existence of an F-chain
![]() $\{B_0, B_1, \ldots \}$
for which
$\{B_0, B_1, \ldots \}$
for which
![]() $\{\mathbf {x}\}= \bigcap _{i}B_i$
; namely, we may simply choose the F-chain associated with a sequence of intervals
$\{\mathbf {x}\}= \bigcap _{i}B_i$
; namely, we may simply choose the F-chain associated with a sequence of intervals
![]() $\{b_i\}_{i \in \mathbb {N}}$
with
$\{b_i\}_{i \in \mathbb {N}}$
with
![]() $b_i \in \mathcal {B}_i$
satisfying
$b_i \in \mathcal {B}_i$
satisfying
![]() $\bigcap _{i \in \mathbb {N}}b_i=\{\mathbf {x}\}$
. It follows that
$\bigcap _{i \in \mathbb {N}}b_i=\{\mathbf {x}\}$
. It follows that
![]() $\mathbf x$
must fall within E and, since
$\mathbf x$
must fall within E and, since
![]() $\mathbf {x}\in \mathcal {K}$
was arbitrary, that
$\mathbf {x}\in \mathcal {K}$
was arbitrary, that
![]() $\mathcal {K} \subseteq E$
as required.
$\mathcal {K} \subseteq E$
as required.
We begin the first step of the inductive process. Given
![]() $\mathcal {B}_0=\{b_0\}$
, the idea is to construct the collection
$\mathcal {B}_0=\{b_0\}$
, the idea is to construct the collection
![]() $\mathcal {B}_1 \subseteq 1/R \mathcal {B}_0$
in such a way that for every
$\mathcal {B}_1 \subseteq 1/R \mathcal {B}_0$
in such a way that for every
![]() $b \in \mathcal {B}_1$
, there exists a place Bob may play his first interval
$b \in \mathcal {B}_1$
, there exists a place Bob may play his first interval
![]() $B_0$
in a
$B_0$
in a
![]() $(1/2, 2/R)$
game so that Alice’s first interval
$(1/2, 2/R)$
game so that Alice’s first interval
![]() $A_1:=F(B_0)$
(as specified by the winning strategy F) contains b; that is, we construct
$A_1:=F(B_0)$
(as specified by the winning strategy F) contains b; that is, we construct
![]() $\mathcal {B}_1$
so that for every
$\mathcal {B}_1$
so that for every
![]() $b \in \mathcal {B}_1$
, there exists an
$b \in \mathcal {B}_1$
, there exists an
![]() $F_1$
-chain
$F_1$
-chain
![]() $\{ B_0 \}$
satisfying
$\{ B_0 \}$
satisfying
![]() $b \subseteq A_1 := F(B_0)$
. For technical reasons, in practice, we will ensure the stronger condition that
$b \subseteq A_1 := F(B_0)$
. For technical reasons, in practice, we will ensure the stronger condition that
![]() $b \subseteq (1-2/R)A_1$
, where
$b \subseteq (1-2/R)A_1$
, where
![]() $\kappa B$
denotes the interval with the same center as B but with radius multiplied by
$\kappa B$
denotes the interval with the same center as B but with radius multiplied by
![]() $\kappa $
.
$\kappa $
.
Recall that for his opening move in a
![]() $(1/2, 2/R)$
game, Bob may choose any interval in
$(1/2, 2/R)$
game, Bob may choose any interval in
![]() $\mathbb {R}$
. In particular, he may choose any interval of radius
$\mathbb {R}$
. In particular, he may choose any interval of radius
![]() $2 \cdot \mathrm {rad}(b_0)$
with center lying in
$2 \cdot \mathrm {rad}(b_0)$
with center lying in
![]() $b_0$
, therefore covering
$b_0$
, therefore covering
![]() $b_0$
. Let
$b_0$
. Let
![]() $\mathcal {W}_1(b_0) \subseteq \mathcal {B}(\mathbb {R})$
be the set of all ‘winning’ intervals for Alice (as prescribed by the winning strategy F) corresponding to any opening interval of this kind that Bob might choose to begin the game with; that is, let
$\mathcal {W}_1(b_0) \subseteq \mathcal {B}(\mathbb {R})$
be the set of all ‘winning’ intervals for Alice (as prescribed by the winning strategy F) corresponding to any opening interval of this kind that Bob might choose to begin the game with; that is, let
Note that this set could either be uncountable or, since for each
![]() $A \in \mathcal {W}_1(b_0)$
, we have
$A \in \mathcal {W}_1(b_0)$
, we have
![]() $\mathrm {rad} (A)=\alpha \cdot (2\cdot \mathrm {rad}(b_0)) = \mathrm {rad}(b_0)$
, it could simply coincide with the singleton
$\mathrm {rad} (A)=\alpha \cdot (2\cdot \mathrm {rad}(b_0)) = \mathrm {rad}(b_0)$
, it could simply coincide with the singleton
![]() $\mathcal {B}_0$
. Moreover, since
$\mathcal {B}_0$
. Moreover, since
![]() $\alpha =1/2$
, we must have for every interval B that
$\alpha =1/2$
, we must have for every interval B that
![]() $\mathrm {cent}(B)$
is contained in
$\mathrm {cent}(B)$
is contained in
![]() $F(B)$
, and so
$F(B)$
, and so
![]() $\mathcal {W}_1(b_0)$
is a cover of
$\mathcal {W}_1(b_0)$
is a cover of
![]() $b_0$
. This property is unique to the case
$b_0$
. This property is unique to the case
![]() $\alpha =1/2$
.
$\alpha =1/2$
.
Lemma 3.10. Let
![]() $b \in \mathcal {B}(\mathbb {R})$
be any closed interval and let
$b \in \mathcal {B}(\mathbb {R})$
be any closed interval and let
![]() $\mathcal {W} \subseteq \mathcal {B}(\mathbb {R})$
be a cover of b by closed intervals of radius
$\mathcal {W} \subseteq \mathcal {B}(\mathbb {R})$
be a cover of b by closed intervals of radius
![]() $\mathrm {rad}(b)$
. Then, for any strictly positive
$\mathrm {rad}(b)$
. Then, for any strictly positive
![]() $\varepsilon < \mathrm {rad}(b)$
, there exists a subset
$\varepsilon < \mathrm {rad}(b)$
, there exists a subset
![]() $\mathcal W^\ast (\varepsilon ) \subseteq \mathcal {W}$
of cardinality at most two that covers b except for an open interval of length at most
$\mathcal W^\ast (\varepsilon ) \subseteq \mathcal {W}$
of cardinality at most two that covers b except for an open interval of length at most
![]() $\varepsilon $
.
$\varepsilon $
.
Proof of Lemma 3.10
Fix n such that
![]() $n^{-1} \mathrm {rad}(b) \leq \varepsilon $
, and let
$n^{-1} \mathrm {rad}(b) \leq \varepsilon $
, and let
![]() $\mathrm {cent}(b) - \mathrm {rad}(b) = x_0,\ \ldots ,\ x_n = \mathrm {cent}(b) + \mathrm {rad}(b)$
be an evenly spaced sequence of points starting and ending at the two endpoints of b. For each
$\mathrm {cent}(b) - \mathrm {rad}(b) = x_0,\ \ldots ,\ x_n = \mathrm {cent}(b) + \mathrm {rad}(b)$
be an evenly spaced sequence of points starting and ending at the two endpoints of b. For each
![]() $i=0,\ldots ,n$
, let
$i=0,\ldots ,n$
, let
![]() $W_i$
be an interval in
$W_i$
be an interval in
![]() $\mathcal {W}$
containing
$\mathcal {W}$
containing
![]() $x_i$
. Now let j be the smallest integer such that
$x_i$
. Now let j be the smallest integer such that
![]() $x_n\in W_j$
. If
$x_n\in W_j$
. If
![]() $j=0$
, then
$j=0$
, then
![]() $W_0 = b$
and we are done. Otherwise, since
$W_0 = b$
and we are done. Otherwise, since
![]() $x_n\notin W_{j-1}$
, we have
$x_n\notin W_{j-1}$
, we have
![]() $x_0\in W_{j-1}$
and thus
$x_0\in W_{j-1}$
and thus
![]() $[x_0,x_{j-1}] \subseteq W_{j-1}$
, whereas
$[x_0,x_{j-1}] \subseteq W_{j-1}$
, whereas
![]() $[x_j,x_n] \subseteq W_j$
. Thus, the intervals
$[x_j,x_n] \subseteq W_j$
. Thus, the intervals
![]() $W_{j-1}$
and
$W_{j-1}$
and
![]() $W_j$
cover b except for the interval
$W_j$
cover b except for the interval
![]() $(x_{j-1},x_j)$
, which is of length at most
$(x_{j-1},x_j)$
, which is of length at most
![]() $\varepsilon $
.
$\varepsilon $
.
We continue the proof of Theorem 1.11. Take
![]() $b=b_0$
,
$b=b_0$
,
![]() $\varepsilon =\mathrm {rad}(b_0)/R$
, and
$\varepsilon =\mathrm {rad}(b_0)/R$
, and
![]() $\mathcal {W}= \mathcal {W}_1$
in Lemma 3.10. Then there exists a subcollection
$\mathcal {W}= \mathcal {W}_1$
in Lemma 3.10. Then there exists a subcollection
![]() $\mathcal {W}_1^\ast :=\{A_1^L, A_1^R\}$
of
$\mathcal {W}_1^\ast :=\{A_1^L, A_1^R\}$
of
![]() $\mathcal {W}_1$
of cardinality at most two covering
$\mathcal {W}_1$
of cardinality at most two covering
![]() $b_0$
except for an open interval
$b_0$
except for an open interval
![]() $I(b_0)$
of length at most
$I(b_0)$
of length at most
![]() $\mathrm {rad}(b)/R$
. It is possible that
$\mathrm {rad}(b)/R$
. It is possible that
![]() $I(b_0)$
is empty. If
$I(b_0)$
is empty. If
![]() $\mathcal {W}_1^\ast $
contains only one interval, say
$\mathcal {W}_1^\ast $
contains only one interval, say
![]() $\mathcal {W}_1^\ast = \{ b'\}$
, then set
$\mathcal {W}_1^\ast = \{ b'\}$
, then set
![]() $A_1^L=A_1^R=b'$
. Let
$A_1^L=A_1^R=b'$
. Let
![]() $B_0^L$
and
$B_0^L$
and
![]() $B_0^R$
be two choices for Bob’s opening move with centers in
$B_0^R$
be two choices for Bob’s opening move with centers in
![]() $b_0$
that satisfy
$b_0$
that satisfy
![]() $A_1^L=F(B_0^L)$
and
$A_1^L=F(B_0^L)$
and
![]() $A_1^R=F(B_0^R)$
; such choices exist by the definition of
$A_1^R=F(B_0^R)$
; such choices exist by the definition of
![]() $\mathcal {W}_1$
. If we had
$\mathcal {W}_1$
. If we had
![]() $A_1^L=A_1^R$
, then assume
$A_1^L=A_1^R$
, then assume
![]() $B_0^L=B_0^R$
.
$B_0^L=B_0^R$
.
We now discard the ‘bad’ intervals that will not appear in the generalized Cantor set
![]() $\mathcal {K}$
. Let
$\mathcal {K}$
. Let
 $$ \begin{align*}\mathbf{Bad}_1:= \bigg\{b' \in \frac{1}{R}\mathcal{B}_0: b'\cap I(b_0) \neq \emptyset\;\text{or}\; b' \not\subseteq ( (1-2/R)A_1^L \cup (1-2/R)A_1^R ) \bigg\}. \end{align*} $$
$$ \begin{align*}\mathbf{Bad}_1:= \bigg\{b' \in \frac{1}{R}\mathcal{B}_0: b'\cap I(b_0) \neq \emptyset\;\text{or}\; b' \not\subseteq ( (1-2/R)A_1^L \cup (1-2/R)A_1^R ) \bigg\}. \end{align*} $$
Since any interval of length
![]() $\mathrm {rad}(b_0)/R$
may intersect at most two intervals from
$\mathrm {rad}(b_0)/R$
may intersect at most two intervals from
![]() ${1}/{R}\mathcal {B}_0$
, and there are at most five intervals (of length at most
${1}/{R}\mathcal {B}_0$
, and there are at most five intervals (of length at most
![]() $\mathrm {rad}(b_0)/R$
) that need to be intersected by
$\mathrm {rad}(b_0)/R$
) that need to be intersected by
![]() $b'$
for it to be in
$b'$
for it to be in
![]() $\mathbf {Bad}_1$
, it is immediate that
$\mathbf {Bad}_1$
, it is immediate that
![]() $\#\mathbf {Bad}_1 \leq 10$
. It follows that
$\#\mathbf {Bad}_1 \leq 10$
. It follows that
![]() $\mathcal {B}_1:= {1}/{R}\mathcal {B}_0 \setminus \mathbf {Bad}_1$
satisfies the required conditions for our generalized Cantor set. For each
$\mathcal {B}_1:= {1}/{R}\mathcal {B}_0 \setminus \mathbf {Bad}_1$
satisfies the required conditions for our generalized Cantor set. For each
![]() $b \in \mathcal {B}_1$
, we associate one of the
$b \in \mathcal {B}_1$
, we associate one of the
![]() $F_1$
-chains
$F_1$
-chains
![]() $\{ B_0^L \}$
or
$\{ B_0^L \}$
or
![]() $\{ B_0^R \}$
, depending on whether b is a subset of
$\{ B_0^R \}$
, depending on whether b is a subset of
![]() $A_1^L$
or
$A_1^L$
or
![]() $A_1^R$
, respectively. If b lies in both
$A_1^R$
, respectively. If b lies in both
![]() $A_1^L$
and
$A_1^L$
and
![]() $A_1^R$
(which is possible if
$A_1^R$
(which is possible if
![]() $I(b_0)$
was empty), then we will assign as a precedent whichever of the intervals
$I(b_0)$
was empty), then we will assign as a precedent whichever of the intervals
![]() $B_0^L$
or
$B_0^L$
or
![]() $B_0^R$
has the ‘leftmost’ center. This completes the first step of the inductive construction process.
$B_0^R$
has the ‘leftmost’ center. This completes the first step of the inductive construction process.
Assume now that we have constructed the collection
![]() $\mathcal {B}_i$
so that for each
$\mathcal {B}_i$
so that for each
![]() $b \in \mathcal {B}_i$
, we have an
$b \in \mathcal {B}_i$
, we have an
![]() $F_i$
-chain
$F_i$
-chain
![]() $\{B_0, \ldots , B_{i-1} \}$
with
$\{B_0, \ldots , B_{i-1} \}$
with
![]() $\mathrm {rad}(B_{i-1})=2R \cdot \mathrm {rad}(b)$
and
$\mathrm {rad}(B_{i-1})=2R \cdot \mathrm {rad}(b)$
and
![]() $b \subseteq (1-2/R)F(B_{i-1})$
. We outline the procedure to construct the subsequent collection
$b \subseteq (1-2/R)F(B_{i-1})$
. We outline the procedure to construct the subsequent collection
![]() $\mathcal {B}_{i+1}$
and the corresponding
$\mathcal {B}_{i+1}$
and the corresponding
![]() $F_{i+1}$
-chains.
$F_{i+1}$
-chains.
Fix
![]() $b \in \mathcal {B}_i$
with associated
$b \in \mathcal {B}_i$
with associated
![]() $F_i$
-chain
$F_i$
-chain
![]() $\{B_0, \ldots , B_{i-1} \}$
. Assume Alice has just played her ith move
$\{B_0, \ldots , B_{i-1} \}$
. Assume Alice has just played her ith move
![]() $A_i:=F(B_{i-1})$
, an interval of radius
$A_i:=F(B_{i-1})$
, an interval of radius
![]() $R \cdot \mathrm {rad}(b)$
, in a
$R \cdot \mathrm {rad}(b)$
, in a
![]() $(1/2, 2/R)$
game corresponding to this
$(1/2, 2/R)$
game corresponding to this
![]() $F_i$
-chain. Bob may then choose any interval of radius
$F_i$
-chain. Bob may then choose any interval of radius
![]() $2 \cdot \mathrm {rad}(b)$
inside
$2 \cdot \mathrm {rad}(b)$
inside
![]() $A_i$
. Since
$A_i$
. Since
![]() $b \subseteq (1-2/R)A_i$
, Bob is free to choose as
$b \subseteq (1-2/R)A_i$
, Bob is free to choose as
![]() $B_i$
any interval of radius
$B_i$
any interval of radius
![]() $2 \cdot \mathrm {rad}(b)$
centered in b; every such choice
$2 \cdot \mathrm {rad}(b)$
centered in b; every such choice
![]() $b'$
will constitute a legal move since
$b'$
will constitute a legal move since
![]() $\mathrm {rad}(b')=2/R \mathrm {rad}(A_i)$
and
$\mathrm {rad}(b')=2/R \mathrm {rad}(A_i)$
and
![]() $b \subseteq (1-2/R)A_i$
together imply
$b \subseteq (1-2/R)A_i$
together imply
![]() $b' \subseteq A_i$
. In particular, the collection
$b' \subseteq A_i$
. In particular, the collection
is a cover of b and consists of candidate ‘winning’ moves that could be played by Alice after any legal move
![]() $B_i$
(with center in b) played by Bob. As before, we apply Lemma 3.10 to find a subset of
$B_i$
(with center in b) played by Bob. As before, we apply Lemma 3.10 to find a subset of
![]() $\mathcal {W}_{i+1}(b)$
of cardinality at most two that covers b except for an open subinterval
$\mathcal {W}_{i+1}(b)$
of cardinality at most two that covers b except for an open subinterval
![]() $I(b)$
of length at most
$I(b)$
of length at most
![]() $\mathrm {rad}(b)/R$
. If the subcover contains two intervals, denote them by
$\mathrm {rad}(b)/R$
. If the subcover contains two intervals, denote them by
![]() $A_{i+1}^L(b)$
and
$A_{i+1}^L(b)$
and
![]() $A_{i+1}^R(b)$
; otherwise, if the subcover consists of a single ball
$A_{i+1}^R(b)$
; otherwise, if the subcover consists of a single ball
![]() $b'$
, then let
$b'$
, then let
![]() $A_{i+1}^L(b)=A_{i+1}^R(b)=b'$
. Denote by
$A_{i+1}^L(b)=A_{i+1}^R(b)=b'$
. Denote by
![]() $B_{i}^L(b)$
and
$B_{i}^L(b)$
and
![]() $B_{i}^R(b)$
some choice of intervals centered in b for which
$B_{i}^R(b)$
some choice of intervals centered in b for which
![]() $A_{i+1}^L(b)=F(B_{i}^L(b))$
and
$A_{i+1}^L(b)=F(B_{i}^L(b))$
and
![]() $A_{i+1}^R(b)=F(B_{i}^R(b))$
, respectively. Define
$A_{i+1}^R(b)=F(B_{i}^R(b))$
, respectively. Define
 $$ \begin{align*}\mathbf{Bad}_{i+1}(b):= \bigg\{&b' \in \frac{1}{R}\{b\}: b'\cap I(b) \neq \emptyset\;\text{or}\; b'\\ &\not\subseteq ( (1-2/R)A_{i+1}^L(b) \cup (1-2/R)A_{i+1}^R(b) ) \bigg\} \end{align*} $$
$$ \begin{align*}\mathbf{Bad}_{i+1}(b):= \bigg\{&b' \in \frac{1}{R}\{b\}: b'\cap I(b) \neq \emptyset\;\text{or}\; b'\\ &\not\subseteq ( (1-2/R)A_{i+1}^L(b) \cup (1-2/R)A_{i+1}^R(b) ) \bigg\} \end{align*} $$
and let
![]() $\mathcal {B}_{i+1}(b):= {1}/{R}\{b\} \setminus \mathbf {Bad}_{i+1}(b)$
. By the same arguments as before, it is clear that
$\mathcal {B}_{i+1}(b):= {1}/{R}\{b\} \setminus \mathbf {Bad}_{i+1}(b)$
. By the same arguments as before, it is clear that
![]() $\#\mathbf {Bad}_{i+1}(b) \leq 10$
for each
$\#\mathbf {Bad}_{i+1}(b) \leq 10$
for each
![]() $b \in \mathcal {B}_i$
.
$b \in \mathcal {B}_i$
.
Finally, for each
![]() $b' \in \mathcal {B}_{i+1}(b)$
, we assign the
$b' \in \mathcal {B}_{i+1}(b)$
, we assign the
![]() $F_{i+1}$
-chain
$F_{i+1}$
-chain
![]() $\{B_0, \ldots , B_{i-1}, B_{i}^L(b) \}$
or
$\{B_0, \ldots , B_{i-1}, B_{i}^L(b) \}$
or
![]() $\{B_0, \ldots , B_{i-1}, B_{i}^R(b_i) \}$
depending on whether
$\{B_0, \ldots , B_{i-1}, B_{i}^R(b_i) \}$
depending on whether
![]() $b'$
lies in
$b'$
lies in
![]() $A_{i+1}^L(b_i)$
or
$A_{i+1}^L(b_i)$
or
![]() $A_{i+1}^R(b_i)$
, respectively. Again, if
$A_{i+1}^R(b_i)$
, respectively. Again, if
![]() $I(b)$
was empty and b was contained in both
$I(b)$
was empty and b was contained in both
![]() $A_{i+1}^L(b)$
and
$A_{i+1}^L(b)$
and
![]() $A_{i+1}^R(b)$
, then we choose whichever of
$A_{i+1}^R(b)$
, then we choose whichever of
![]() $B_{i}^L(b)$
and
$B_{i}^L(b)$
and
![]() $B_{i}^R(b)$
has the leftmost center as a convention.
$B_{i}^R(b)$
has the leftmost center as a convention.
Upon setting
 $$ \begin{align*}\mathcal{B}_{i+1}:= \bigcup_{b \in \mathcal{B}_i}\mathcal{B}_{i+1}(b),\end{align*} $$
$$ \begin{align*}\mathcal{B}_{i+1}:= \bigcup_{b \in \mathcal{B}_i}\mathcal{B}_{i+1}(b),\end{align*} $$
we see that the conditions of our generalized Cantor set
![]() $\mathcal {K}(b_0,R,10)$
are satisfied. This completes the inductive procedure.
$\mathcal {K}(b_0,R,10)$
are satisfied. This completes the inductive procedure.
3.5. Cantor rich and Cantor winning
In this section, we prove the following statement which implies Theorem 1.13.
Theorem 3.11. Let
![]() $(X,\mathcal {S},U,f)$
be a splitting structure, let
$(X,\mathcal {S},U,f)$
be a splitting structure, let
![]() $B_0\subseteq X$
be any ball, and let
$B_0\subseteq X$
be any ball, and let
![]() $\varepsilon>0$
be a real number. If
$\varepsilon>0$
be a real number. If
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $\varepsilon $
Cantor winning in
$\varepsilon $
Cantor winning in
![]() $B_0$
, then it is
$B_0$
, then it is
![]() $(B_0,M)$
Cantor rich with
$(B_0,M)$
Cantor rich with
Conversely, assume that X is doubling and let
![]() $M\geqslant 4$
be a real number. If E is
$M\geqslant 4$
be a real number. If E is
![]() $(B_0,M)$
Cantor rich, then it is
$(B_0,M)$
Cantor rich, then it is
![]() $\varepsilon $
Cantor winning in
$\varepsilon $
Cantor winning in
![]() $B_0$
, for any
$B_0$
, for any
![]() $\varepsilon $
for which there exists
$\varepsilon $
for which there exists
![]() $R\in U$
such that
$R\in U$
such that
In particular, if
![]() $X=\mathbb {R}$
with the standard splitting structure, then E is M Cantor rich if and only if it is
$X=\mathbb {R}$
with the standard splitting structure, then E is M Cantor rich if and only if it is
![]() $\varepsilon $
Cantor winning with
$\varepsilon $
Cantor winning with
 $$ \begin{align*} \varepsilon = \log_4 \bigg(\frac{1}{\lfloor M\rfloor +1}\bigg). \end{align*} $$
$$ \begin{align*} \varepsilon = \log_4 \bigg(\frac{1}{\lfloor M\rfloor +1}\bigg). \end{align*} $$
Proof. Assume E is
![]() $\varepsilon $
Cantor winning in
$\varepsilon $
Cantor winning in
![]() $B_0$
. Then, by Corollary 3.3, for every
$B_0$
. Then, by Corollary 3.3, for every
![]() $2\leq R\in U$
, there exists a
$2\leq R\in U$
, there exists a
![]() $(B_{0},R,f(R)^{1-\varepsilon })$
Cantor set contained in E. Fix an integer R such that
$(B_{0},R,f(R)^{1-\varepsilon })$
Cantor set contained in E. Fix an integer R such that
![]() $f(R)>M$
and a real number
$f(R)>M$
and a real number
![]() $y>0$
. Since
$y>0$
. Since
![]() ${4}/{f(R)}^{\varepsilon }<1$
, we can choose
${4}/{f(R)}^{\varepsilon }<1$
, we can choose
![]() $\ell>0$
such that
$\ell>0$
such that
![]() ${4}/{f(R)}\cdot ({4}/{f(R)}^{\varepsilon })^{\ell }<y$
. Consider a
${4}/{f(R)}\cdot ({4}/{f(R)}^{\varepsilon })^{\ell }<y$
. Consider a
![]() $(B_{0},R^{\ell },f(R)^{\ell (1-\varepsilon )})$
Cantor set contained in E and denote its Cantor sequence by
$(B_{0},R^{\ell },f(R)^{\ell (1-\varepsilon )})$
Cantor set contained in E and denote its Cantor sequence by
![]() $\{ \mathcal {B}_{n}\} _{n=0}^{\infty }$
. Define another Cantor sequence
$\{ \mathcal {B}_{n}\} _{n=0}^{\infty }$
. Define another Cantor sequence
![]() $\{ \mathcal {B}_{n}'\} _{n=0}^{\infty }$
by setting
$\{ \mathcal {B}_{n}'\} _{n=0}^{\infty }$
by setting
![]() $\mathcal {B}^{\prime }_{\ell k}=\mathcal {B}_{k}$
for all
$\mathcal {B}^{\prime }_{\ell k}=\mathcal {B}_{k}$
for all
![]() $k\geq 0$
and
$k\geq 0$
and
![]() $\mathcal {B}_{n}'={1}/{R}\mathcal {B}_{n-1}$
whenever
$\mathcal {B}_{n}'={1}/{R}\mathcal {B}_{n-1}$
whenever
![]() $n\neq \ell k$
. Then the limit set
$n\neq \ell k$
. Then the limit set
 $$ \begin{align*} \bigcap_{n=1}^\infty \bigcup_{B\in \mathcal{B}_{n}'} B \end{align*} $$
$$ \begin{align*} \bigcap_{n=1}^\infty \bigcup_{B\in \mathcal{B}_{n}'} B \end{align*} $$
is a
![]() $(B_{0},R,(r_{m,n})_{0\leq m\leq n})$
generalized Cantor set, with
$(B_{0},R,(r_{m,n})_{0\leq m\leq n})$
generalized Cantor set, with
![]() $r_{\ell (k-1), \ell k}=f(R)^{\ell (1-\varepsilon )}$
for all
$r_{\ell (k-1), \ell k}=f(R)^{\ell (1-\varepsilon )}$
for all
![]() $k\geq 0$
, and
$k\geq 0$
, and
![]() $r_{m,n}=0$
for all other pairs. Then, for any
$r_{m,n}=0$
for all other pairs. Then, for any
![]() $k>0$
and
$k>0$
and
![]() $n = \ell k$
, we get
$n = \ell k$
, we get
 $$ \begin{align*} \sum_{m=0}^{\ell k}\bigg(\frac{4}{f(R)}\bigg)^{\ell k-m +1}r_{m,\ell k}=\bigg(\frac{4}{f(R)}\bigg)^{\ell+1}f(R)^{\ell(1-\varepsilon)}=\frac{4}{f(R)}\cdot \bigg(\frac{4}{f(R)^{\varepsilon}}\bigg)^{\ell}<y. \end{align*} $$
$$ \begin{align*} \sum_{m=0}^{\ell k}\bigg(\frac{4}{f(R)}\bigg)^{\ell k-m +1}r_{m,\ell k}=\bigg(\frac{4}{f(R)}\bigg)^{\ell+1}f(R)^{\ell(1-\varepsilon)}=\frac{4}{f(R)}\cdot \bigg(\frac{4}{f(R)^{\varepsilon}}\bigg)^{\ell}<y. \end{align*} $$
For every
![]() $n\neq \ell k$
, we have
$n\neq \ell k$
, we have
 $$ \begin{align*} \sum_{m=0}^{n}\bigg(\frac{4}{f(R)}\bigg)^{n-m+1}r_{m,n}=0<y. \end{align*} $$
$$ \begin{align*} \sum_{m=0}^{n}\bigg(\frac{4}{f(R)}\bigg)^{n-m+1}r_{m,n}=0<y. \end{align*} $$
For the other direction, suppose that E is
![]() $(B_0,M)$
Cantor rich. Let
$(B_0,M)$
Cantor rich. Let
![]() $c_0 = \delta (1-\varepsilon )$
. By Theorem 3.4, it is enough to show that E is
$c_0 = \delta (1-\varepsilon )$
. By Theorem 3.4, it is enough to show that E is
![]() $c_0$
potential winning in
$c_0$
potential winning in
![]() $B_0$
. We argue as in the proof of Theorem 3.4. Choose R such that
$B_0$
. We argue as in the proof of Theorem 3.4. Choose R such that
![]() $M < f(R) \leq 4^{1/\varepsilon }$
and fix any
$M < f(R) \leq 4^{1/\varepsilon }$
and fix any
![]() $0 < \beta \leq {1}/{R}$
,
$0 < \beta \leq {1}/{R}$
,
![]() $c> c_0$
. Fix a small enough
$c> c_0$
. Fix a small enough
![]() $y>0$
whose precise value will be determined later. By the definition of Cantor rich, E contains some
$y>0$
whose precise value will be determined later. By the definition of Cantor rich, E contains some
![]() $(B_0,R,\mathbf {r})$
Cantor set
$(B_0,R,\mathbf {r})$
Cantor set
![]() $\mathcal {K}$
, where
$\mathcal {K}$
, where
![]() $\mathbf {r}$
satisfies
$\mathbf {r}$
satisfies
 $$ \begin{align*} \sum_{m=0}^{n} \bigg(\frac{4}{f(R)}\bigg)^{n-m+1}r_{m,n} < y \end{align*} $$
$$ \begin{align*} \sum_{m=0}^{n} \bigg(\frac{4}{f(R)}\bigg)^{n-m+1}r_{m,n} < y \end{align*} $$
for every
![]() $n\in \mathbb {N}$
. In particular, for every
$n\in \mathbb {N}$
. In particular, for every
![]() $m,n\in \mathbb {N}$
, we have
$m,n\in \mathbb {N}$
, we have
 $$ \begin{align*} r_{m,n} < y\bigg(\frac{f(R)}{4}\bigg)^{n-m+1} \leq yR^{(n-m+1)c_0}. \end{align*} $$
$$ \begin{align*} r_{m,n} < y\bigg(\frac{f(R)}{4}\bigg)^{n-m+1} \leq yR^{(n-m+1)c_0}. \end{align*} $$
We now describe a strategy for Alice to win the
![]() $(c,\beta )$
potential game on
$(c,\beta )$
potential game on
![]() $A_\infty (B_0)$
. As in the proof of Theorem 3.4, let
$A_\infty (B_0)$
. As in the proof of Theorem 3.4, let
![]() $\rho $
denote the radius of
$\rho $
denote the radius of
![]() $B_0$
, let
$B_0$
, let
![]() $D_k$
denote Bob’s kth move, and for each
$D_k$
denote Bob’s kth move, and for each
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $m = m_k\in \mathbb {N}$
denote an integer such that
$m = m_k\in \mathbb {N}$
denote an integer such that
![]() $\beta \cdot \mathrm {rad}(D_k) < R^{-m}\rho \leq \mathrm {rad}(D_k)$
. The inequality
$\beta \cdot \mathrm {rad}(D_k) < R^{-m}\rho \leq \mathrm {rad}(D_k)$
. The inequality
![]() $\beta \leqslant 1/R$
ensures that such m exists. Then Alice’s strategy is as follows: on turn k, remove all elements of the set
$\beta \leqslant 1/R$
ensures that such m exists. Then Alice’s strategy is as follows: on turn k, remove all elements of the set
that intersect Bob’s current choice. This strategy, if executable, will make Alice win since the intersection of Bob’s balls will satisfy
![]() $\bigcap _{k \in \mathbb {N}}D_k \subseteq \mathcal {K} \subseteq E$
. To show that it is legal, we need to show that
$\bigcap _{k \in \mathbb {N}}D_k \subseteq \mathcal {K} \subseteq E$
. To show that it is legal, we need to show that
 $$ \begin{align} \sum_{\substack{B\in \mathcal{B}_m \\ B\cap D_k \neq \varnothing}} \sum_{n \geq m} r_{m,n} (R^{-(n + 1)}\rho)^c \leq (\beta\cdot \mathrm{rad}(D_k))^c. \end{align} $$
$$ \begin{align} \sum_{\substack{B\in \mathcal{B}_m \\ B\cap D_k \neq \varnothing}} \sum_{n \geq m} r_{m,n} (R^{-(n + 1)}\rho)^c \leq (\beta\cdot \mathrm{rad}(D_k))^c. \end{align} $$
This is enough because elements of
![]() $\mathcal {A}_{m,n}(B)$
all have radius
$\mathcal {A}_{m,n}(B)$
all have radius
![]() $R^{-(n + 1)}\rho $
. Since the elements of
$R^{-(n + 1)}\rho $
. Since the elements of
![]() $\mathcal {B}_m$
are disjoint and have radius
$\mathcal {B}_m$
are disjoint and have radius
![]() $R^{-m} \rho \asymp _\beta \mathrm {rad}(D_k)$
, the number of them that intersect
$R^{-m} \rho \asymp _\beta \mathrm {rad}(D_k)$
, the number of them that intersect
![]() $D_k$
is bounded by a constant depending only on
$D_k$
is bounded by a constant depending only on
![]() $\beta $
. Call this constant
$\beta $
. Call this constant
![]() $C_1$
. Then the left-hand side of equation (26) is less than
$C_1$
. Then the left-hand side of equation (26) is less than
 $$ \begin{align*} C_1 \sum_{n\geq m} yR^{(n - m + 1)c_0} \bigg(R^{-(n + 1)}\rho\bigg)^c &= C_1 (R^{-m} \rho)^c y\sum_{\ell = 1}^\infty R^{(c_0 - c)\ell}\\ &\leqslant C_1(\mathrm{rad}(D_k))^c\frac{R^{(c_0 - c)}}{1 - R^{(c_0 - c)}} y. \end{align*} $$
$$ \begin{align*} C_1 \sum_{n\geq m} yR^{(n - m + 1)c_0} \bigg(R^{-(n + 1)}\rho\bigg)^c &= C_1 (R^{-m} \rho)^c y\sum_{\ell = 1}^\infty R^{(c_0 - c)\ell}\\ &\leqslant C_1(\mathrm{rad}(D_k))^c\frac{R^{(c_0 - c)}}{1 - R^{(c_0 - c)}} y. \end{align*} $$
By choosing y so that
 $$ \begin{align*} y < \frac{\beta^c (1 - R^{(c_0 - c)})}{C_1R^{(c_0 - c)}}, \end{align*} $$
$$ \begin{align*} y < \frac{\beta^c (1 - R^{(c_0 - c)})}{C_1R^{(c_0 - c)}}, \end{align*} $$
we guarantee that the move is legal.
4. Intersection with fractals
The concept of winning sets gives a notion of largeness which is orthogonal to both category and measure. It was first noticed in [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11] that absolute winning subsets of
![]() $\mathbb {R}^N$
are also large in a dual sense: they intersect every non-empty diffuse set. The Cantor and the potential games, together with the definition of the Ahlfors regularity dimension, allow us to quantify this observation. Based on the Borel determinacy property for Schmidt games [Reference Fishman, Ly and Simmons25], we also prove a partial converse.
$\mathbb {R}^N$
are also large in a dual sense: they intersect every non-empty diffuse set. The Cantor and the potential games, together with the definition of the Ahlfors regularity dimension, allow us to quantify this observation. Based on the Borel determinacy property for Schmidt games [Reference Fishman, Ly and Simmons25], we also prove a partial converse.
Theorem 4.1. If
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $c_0$
potential winning, then
$c_0$
potential winning, then
![]() $E\cap K\neq \emptyset $
for every closed set
$E\cap K\neq \emptyset $
for every closed set
![]() $K\subseteq ~X$
with
$K\subseteq ~X$
with
![]() $\dim _R K> c_0$
. If E is Borel, then the converse holds.
$\dim _R K> c_0$
. If E is Borel, then the converse holds.
Combining this with Propositions 2.18 and 1.3 yields the following corollary.
Corollary 4.2. If
![]() $E\subseteq X$
is Borel and
$E\subseteq X$
is Borel and
![]() $E\cap K\neq \emptyset $
for any diffuse set K, then E is absolute winning.
$E\cap K\neq \emptyset $
for any diffuse set K, then E is absolute winning.
Remark 4.3. One can check that Theorem 1.14 follows from Theorem 4.1 together with Theorem 3.4. Indeed, by Theorem 3.4, the set
![]() $E\in \mathbb {R}^N$
is
$E\in \mathbb {R}^N$
is
![]() $\varepsilon _0$
Cantor winning if and only if it is
$\varepsilon _0$
Cantor winning if and only if it is
![]() $c_0$
potential winning for
$c_0$
potential winning for
![]() $c_0 = N(1-\varepsilon _0)$
. Then, Theorem 1.14 is a straightforward corollary of Theorem 4.1.
$c_0 = N(1-\varepsilon _0)$
. Then, Theorem 1.14 is a straightforward corollary of Theorem 4.1.
We will need the following observation regarding the potential game.
Lemma 4.4. Let X be a complete metric space,
![]() $K\subseteq X$
a closed subset, and let
$K\subseteq X$
a closed subset, and let
![]() $c>0$
. If
$c>0$
. If
![]() $E\subseteq X$
is c potential winning in X, then
$E\subseteq X$
is c potential winning in X, then
![]() $E\cap K$
is c potential winning in K.
$E\cap K$
is c potential winning in K.
Proof. Assume
![]() $c'>c$
and
$c'>c$
and
![]() $\beta>0$
, and fix a winning strategy for Alice on E for the
$\beta>0$
, and fix a winning strategy for Alice on E for the
![]() $(c',\beta )$
potential game on X. Define a winning strategy for Alice on
$(c',\beta )$
potential game on X. Define a winning strategy for Alice on
![]() $E\cap K$
for the
$E\cap K$
for the
![]() $(c',3\beta )$
potential game on K as follows. Assume
$(c',3\beta )$
potential game on K as follows. Assume
![]() $i\geq 0$
and that
$i\geq 0$
and that
![]() $B_i=B(x_i,r_i)\subseteq K$
with
$B_i=B(x_i,r_i)\subseteq K$
with
![]() $x_i\in K$
is chosen by Bob in his ith move. Consider the ball with the same center and radius in X, and apply the winning strategy of Alice on X to get a collection of balls
$x_i\in K$
is chosen by Bob in his ith move. Consider the ball with the same center and radius in X, and apply the winning strategy of Alice on X to get a collection of balls
![]() $\mathcal {A}_{i+1}$
. For every
$\mathcal {A}_{i+1}$
. For every
![]() $A\in \mathcal {A}_i$
for which
$A\in \mathcal {A}_i$
for which
![]() $A\cap K\neq \varnothing $
, fix a point
$A\cap K\neq \varnothing $
, fix a point
![]() $z(A)\in A\cap K$
. The triangle inequality implies that
$z(A)\in A\cap K$
. The triangle inequality implies that
![]() $A\cap K\subseteq B(z(A),3\mathrm {rad}(A))$
for every
$A\cap K\subseteq B(z(A),3\mathrm {rad}(A))$
for every
![]() $A\in \mathcal {A}_{i+1}$
. For the game in K, Alice will choose the collection of balls in K defined by
$A\in \mathcal {A}_{i+1}$
. For the game in K, Alice will choose the collection of balls in K defined by
On one hand,
 $$ \begin{align*} \sum_{A\in\mathcal{A}^{\prime}_{i+1}} \mathrm{rad}(A)^{c'} \leq 3^{c'}\sum_{A\in\mathcal{A}_{i+1}} \mathrm{rad}(A)^{c'} < 3^{c'}(\beta\cdot\mathrm{rad}(B_i))^{c'} = (3\beta\cdot\mathrm{rad}(B_i))^{c'} \end{align*} $$
$$ \begin{align*} \sum_{A\in\mathcal{A}^{\prime}_{i+1}} \mathrm{rad}(A)^{c'} \leq 3^{c'}\sum_{A\in\mathcal{A}_{i+1}} \mathrm{rad}(A)^{c'} < 3^{c'}(\beta\cdot\mathrm{rad}(B_i))^{c'} = (3\beta\cdot\mathrm{rad}(B_i))^{c'} \end{align*} $$
and, therefore, this move is legal. On the other hand,
 $$ \begin{align*} \bigcup_{A\in\mathcal{A}_{i+1}}A\cap K\subseteq\bigcup_{A\in\mathcal{A}^{\prime}_{i+1}}A. \end{align*} $$
$$ \begin{align*} \bigcup_{A\in\mathcal{A}_{i+1}}A\cap K\subseteq\bigcup_{A\in\mathcal{A}^{\prime}_{i+1}}A. \end{align*} $$
Since K is closed, applying this strategy for every i guarantees that, if
![]() $\mathrm {rad}(B_i)\to 0$
, then either
$\mathrm {rad}(B_i)\to 0$
, then either
 $$ \begin{align*} \bigcap_{i=0}^\infty B_i\subseteq E\cap K \end{align*} $$
$$ \begin{align*} \bigcap_{i=0}^\infty B_i\subseteq E\cap K \end{align*} $$
or
 $$ \begin{align*} \bigcap_{i=0}^\infty B_i\subseteq \bigcup_{i=1}^\infty\bigcup_{A\in\mathcal{A}^{\prime}_i}A. \end{align*} $$
$$ \begin{align*} \bigcap_{i=0}^\infty B_i\subseteq \bigcup_{i=1}^\infty\bigcup_{A\in\mathcal{A}^{\prime}_i}A. \end{align*} $$
This shows that
![]() $E\cap K$
is
$E\cap K$
is
![]() $(c',3\beta )$
potential winning for every
$(c',3\beta )$
potential winning for every
![]() $c'>c$
and
$c'>c$
and
![]() $\beta>0$
, and hence, it is c potential winning.
$\beta>0$
, and hence, it is c potential winning.
Proof of Theorem 4.1
Assume that
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $c_0$
potential winning and let
$c_0$
potential winning and let
![]() $K\subseteq X$
be a c Ahlfors regular set with
$K\subseteq X$
be a c Ahlfors regular set with
![]() $c>c_0$
. Lemma 4.4 implies that
$c>c_0$
. Lemma 4.4 implies that
![]() $E\cap K$
is winning for the
$E\cap K$
is winning for the
![]() $c_0$
potential game restricted to K. Therefore, by Theorem 3.8,
$c_0$
potential game restricted to K. Therefore, by Theorem 3.8,
![]() $E\cap K$
contains an
$E\cap K$
contains an
![]() $(\alpha , \beta )$
winning set for certain pairs
$(\alpha , \beta )$
winning set for certain pairs
![]() $(\alpha ,\beta )$
and hence it is non-empty.
$(\alpha ,\beta )$
and hence it is non-empty.
For the converse, assume E is Borel, and that E is not
![]() $c_0$
potential winning. By the Borel determinacy theorem [Reference Fishman, Ly and Simmons25, Theorem 3.1], Bob has a winning strategy to make sure the
$c_0$
potential winning. By the Borel determinacy theorem [Reference Fishman, Ly and Simmons25, Theorem 3.1], Bob has a winning strategy to make sure the
![]() $c_0$
potential game ends in
$c_0$
potential game ends in
![]() $X\setminus E$
. (In fact, [Reference Fishman, Ly and Simmons25, Theorem 3.1] does not deal with potential games. However, its proof can be easily modified to cover them. In the notation of that paper, it is clear from the definition of who wins the potential game that there exists a Borel set
$X\setminus E$
. (In fact, [Reference Fishman, Ly and Simmons25, Theorem 3.1] does not deal with potential games. However, its proof can be easily modified to cover them. In the notation of that paper, it is clear from the definition of who wins the potential game that there exists a Borel set
![]() $A\subseteq Z\times X$
such that if
$A\subseteq Z\times X$
such that if
![]() $\omega \in E_\Gamma $
is a play of the game, then
$\omega \in E_\Gamma $
is a play of the game, then
![]() $\omega $
is a win for Alice if and only if either
$\omega $
is a win for Alice if and only if either
![]() $\omega \notin Z$
or
$\omega \notin Z$
or
![]() $(\omega ,\iota (\omega )) \in B$
. Combining with [Reference Fishman, Ly and Simmons25, Lemma 3.3] shows that the set of plays of the game that result in a win for Alice is Borel.) Fix this strategy and let
$(\omega ,\iota (\omega )) \in B$
. Combining with [Reference Fishman, Ly and Simmons25, Lemma 3.3] shows that the set of plays of the game that result in a win for Alice is Borel.) Fix this strategy and let
![]() $\beta> 0$
and
$\beta> 0$
and
![]() $c> c_0$
be Bob’s choices according to this strategy. We will show that
$c> c_0$
be Bob’s choices according to this strategy. We will show that
![]() $X\setminus E$
contains Ahlfors regular sets of dimension arbitrarily close to c.
$X\setminus E$
contains Ahlfors regular sets of dimension arbitrarily close to c.
Fix a small number
![]() $\gamma> 0$
. Denote by
$\gamma> 0$
. Denote by
![]() $\mathcal {A}_{i+1}$
the collection of balls chosen by Alice in response to Bob’s ith move
$\mathcal {A}_{i+1}$
the collection of balls chosen by Alice in response to Bob’s ith move
![]() $B_i$
. We will consider strategies for Alice where she only chooses non-empty collections on some turns, namely
$B_i$
. We will consider strategies for Alice where she only chooses non-empty collections on some turns, namely
![]() $\mathcal {A}_{i+1}\neq \emptyset $
only if
$\mathcal {A}_{i+1}\neq \emptyset $
only if
Such turns
![]() $i = i(n)$
will be called good turns. If
$i = i(n)$
will be called good turns. If
![]() $B_0,\ldots ,B_{i(n)}$
versus
$B_0,\ldots ,B_{i(n)}$
versus
![]() $\mathcal {A}_1,\ldots ,\mathcal {A}_{i(n)+1}$
is a history of the game, then we let
$\mathcal {A}_1,\ldots ,\mathcal {A}_{i(n)+1}$
is a history of the game, then we let
![]() $f(\mathcal {A}_{i(n)+1})$
denote the next ball that Bob plays on a good turn if the game continues with Bob playing his winning strategy and Alice playing dummy moves (that is, choosing the empty collection), that is,
$f(\mathcal {A}_{i(n)+1})$
denote the next ball that Bob plays on a good turn if the game continues with Bob playing his winning strategy and Alice playing dummy moves (that is, choosing the empty collection), that is,
![]() $f(\mathcal {A}_{i(n)+1}):= B_{i(n+1)}$
. Next, we let
$f(\mathcal {A}_{i(n)+1}):= B_{i(n+1)}$
. Next, we let
 $$ \begin{align*} N = \bigg\lfloor \bigg(\frac{\beta^2}{3\gamma}\bigg)^c \bigg\rfloor. \end{align*} $$
$$ \begin{align*} N = \bigg\lfloor \bigg(\frac{\beta^2}{3\gamma}\bigg)^c \bigg\rfloor. \end{align*} $$
If
![]() $B_0,\ldots ,B_{i(n)}$
versus
$B_0,\ldots ,B_{i(n)}$
versus
![]() $\mathcal {A}_1,\ldots ,\mathcal {A}_{i(n)}$
is a history of the game, then we define a sequence of balls
$\mathcal {A}_1,\ldots ,\mathcal {A}_{i(n)}$
is a history of the game, then we define a sequence of balls
![]() $( g_k(B_{i(n)}) )_{k = 1}^N$
by recursion: we let
$( g_k(B_{i(n)}) )_{k = 1}^N$
by recursion: we let
![]() $g_1(B_{i(n)}):= f(\emptyset )$
, and if
$g_1(B_{i(n)}):= f(\emptyset )$
, and if
![]() $g_1,\ldots ,g_{k-1}$
are defined for some
$g_1,\ldots ,g_{k-1}$
are defined for some
![]() $k\geq 1$
, then we let
$k\geq 1$
, then we let
Here,
![]() $\mathcal N(A,d)$
denotes the d-neighborhood of a set A, that is,
$\mathcal N(A,d)$
denotes the d-neighborhood of a set A, that is,
![]() $\mathcal N(A,d):=\{x\in X: \mathbf {d}(A,x)\leqslant d\}$
. We will show later (using the definition of N) that it is legal for Alice to play the collection appearing in the right-hand side, and hence the right-hand side is well defined. Note that since
$\mathcal N(A,d):=\{x\in X: \mathbf {d}(A,x)\leqslant d\}$
. We will show later (using the definition of N) that it is legal for Alice to play the collection appearing in the right-hand side, and hence the right-hand side is well defined. Note that since
![]() $B_{i(n)}$
is the nth good turn in the history
$B_{i(n)}$
is the nth good turn in the history
![]() $B_0,\ldots ,B_{i(n)}$
versus
$B_0,\ldots ,B_{i(n)}$
versus
![]() $\mathcal {A}_1,\ldots ,\mathcal {A}_{i(n)}$
, for each
$\mathcal {A}_1,\ldots ,\mathcal {A}_{i(n)}$
, for each
![]() $k=1,\ldots ,N$
,
$k=1,\ldots ,N$
,
![]() $g_k(B_{i(n)})$
is the
$g_k(B_{i(n)})$
is the
![]() $(n+1)$
st good turn in its corresponding history. We call these balls the children of
$(n+1)$
st good turn in its corresponding history. We call these balls the children of
![]() $B_{i(n)}$
. The children of
$B_{i(n)}$
. The children of
![]() $B_{i(n)}$
are disjoint, because if
$B_{i(n)}$
are disjoint, because if
![]() $g_j(B_{i(n)}) \cap g_k(B_{i(n)}) \neq \emptyset $
for some
$g_j(B_{i(n)}) \cap g_k(B_{i(n)}) \neq \emptyset $
for some
![]() $j,k$
with
$j,k$
with
![]() $j < k$
, then
$j < k$
, then
![]() $g_k(B_{i(n)}) \subseteq \mathcal N(g_j(B_{i(n)}),\gamma ^{n+1} \mathrm {diam}(B_0))$
, and thus Alice wins by default in the game in which Bob played his winning strategy ending in move
$g_k(B_{i(n)}) \subseteq \mathcal N(g_j(B_{i(n)}),\gamma ^{n+1} \mathrm {diam}(B_0))$
, and thus Alice wins by default in the game in which Bob played his winning strategy ending in move
![]() $g_k(B_{i(n)})$
, which is a contradiction.
$g_k(B_{i(n)})$
, which is a contradiction.
Now construct a Cantor set
![]() $\mathcal {K}$
as follows: let
$\mathcal {K}$
as follows: let
![]() $\mathcal {B}_0 = \{B_0\}$
, and if
$\mathcal {B}_0 = \{B_0\}$
, and if
![]() $\mathcal {B}_n$
is defined, then let
$\mathcal {B}_n$
is defined, then let
![]() $\mathcal {B}_{n+1}$
be the collection of children of elements of
$\mathcal {B}_{n+1}$
be the collection of children of elements of
![]() $\mathcal {B}_n$
according to the above construction. Note that
$\mathcal {B}_n$
according to the above construction. Note that
![]() $\mathcal {B}_n$
consists of moves for Bob that are the nth good turns with respect to their corresponding histories and, in particular,
$\mathcal {B}_n$
consists of moves for Bob that are the nth good turns with respect to their corresponding histories and, in particular,
![]() $\beta \gamma ^n\mathrm {rad}(B_0) < \mathrm {rad}(B) \leq \gamma ^n \mathrm {rad}(B_0)$
for all
$\beta \gamma ^n\mathrm {rad}(B_0) < \mathrm {rad}(B) \leq \gamma ^n \mathrm {rad}(B_0)$
for all
![]() $B\in \mathcal {B}_n$
. Finally, let
$B\in \mathcal {B}_n$
. Finally, let
![]() $\mathcal {K} = \bigcap _{n\in \mathbb {N}} \bigcup _{B\in \mathcal {B}_n} B$
. Any element of
$\mathcal {K} = \bigcap _{n\in \mathbb {N}} \bigcup _{B\in \mathcal {B}_n} B$
. Any element of
![]() $\mathcal {K}$
is the outcome of some game in which Bob played his winning strategy, so
$\mathcal {K}$
is the outcome of some game in which Bob played his winning strategy, so
![]() $\mathcal {K}\subseteq X\setminus E$
. Moreover, from the construction of
$\mathcal {K}\subseteq X\setminus E$
. Moreover, from the construction of
![]() $\mathcal {K}$
, it is clear that
$\mathcal {K}$
, it is clear that
![]() $\mathcal {K}$
is Ahlfors regular of dimension
$\mathcal {K}$
is Ahlfors regular of dimension
![]() $({\log N})/({-\log \gamma })$
. From the definition of N, we see that this dimension tends to c as
$({\log N})/({-\log \gamma })$
. From the definition of N, we see that this dimension tends to c as
![]() $\gamma \to 0$
.
$\gamma \to 0$
.
To complete the proof, we need to show that it is legal for Alice to play the collection
for any
![]() $k\leq N$
. Indeed, the cost of this collection is
$k\leq N$
. Indeed, the cost of this collection is
 $$ \begin{align*} \sum_{j=1}^{k-1} (\mathrm{rad}(g_j(B_{i(n)})) + \gamma^{n+1} \mathrm{diam}(B_j))^c &\leq N (3\gamma^{n+1} \mathrm{rad}(B_0))^c \\ \leq (\beta^2 \gamma^n \mathrm{rad}(B_0))^c &\leq (\beta \cdot \mathrm{rad}(B_{i(n)}))^c.\\[-35pt] \end{align*} $$
$$ \begin{align*} \sum_{j=1}^{k-1} (\mathrm{rad}(g_j(B_{i(n)})) + \gamma^{n+1} \mathrm{diam}(B_j))^c &\leq N (3\gamma^{n+1} \mathrm{rad}(B_0))^c \\ \leq (\beta^2 \gamma^n \mathrm{rad}(B_0))^c &\leq (\beta \cdot \mathrm{rad}(B_{i(n)}))^c.\\[-35pt] \end{align*} $$
Remark 4.5. A similar characterization is possible in the generality of
![]() $\mathcal {H}$
potential games.
$\mathcal {H}$
potential games.
In fact, potential winning sets not only have non-empty intersection with Ahlfors regular sets, but the intersection has full Hausdorff dimension. To prove this, let us first prove the following.
Proposition 4.6. If
![]() ${\dim _H}(E) \leq c_0$
, then
${\dim _H}(E) \leq c_0$
, then
![]() $X\setminus E$
is
$X\setminus E$
is
![]() $c_0$
potential winning.
$c_0$
potential winning.
Proof. Fix
![]() $\beta> 0$
,
$\beta> 0$
,
![]() $c> c_0$
, and
$c> c_0$
, and
![]() $r_0> 0$
. Since the c-dimensional Hausdorff measure of E is zero, there exists a cover
$r_0> 0$
. Since the c-dimensional Hausdorff measure of E is zero, there exists a cover
![]() $\mathcal {C}$
of E such that
$\mathcal {C}$
of E such that
Thus, if Bob’s first ball has radius
![]() $r_0$
, then Alice can legally remove the collection
$r_0$
, then Alice can legally remove the collection
![]() $\mathcal {C}$
, thus deleting the entire set E on her first turn.
$\mathcal {C}$
, thus deleting the entire set E on her first turn.
Theorem 4.7. If
![]() $c_0 < \delta =\dim _R X$
, then every
$c_0 < \delta =\dim _R X$
, then every
![]() $c_0$
potential winning set in X has Hausdorff dimension
$c_0$
potential winning set in X has Hausdorff dimension
![]() $\delta $
.
$\delta $
.
Proof. By contradiction, suppose that
![]() $E\subseteq X$
is
$E\subseteq X$
is
![]() $c_0$
potential winning but
$c_0$
potential winning but
![]() $c_1 := {\dim _H}(E) < \delta $
. Then by Proposition 4.6,
$c_1 := {\dim _H}(E) < \delta $
. Then by Proposition 4.6,
![]() $X\setminus E$
is
$X\setminus E$
is
![]() $c_1$
potential winning, so by the intersection property (W2) (see Proposition 2.4), the empty set
$c_1$
potential winning, so by the intersection property (W2) (see Proposition 2.4), the empty set
![]() $\emptyset $
is
$\emptyset $
is
![]() $c_2$
potential winning, where
$c_2$
potential winning, where
![]() $c_2 = \max (c_0,c_1) < \delta $
. However, then by Theorem 3.8, the empty set
$c_2 = \max (c_0,c_1) < \delta $
. However, then by Theorem 3.8, the empty set
![]() $\emptyset $
is
$\emptyset $
is
![]() $(\alpha ,\beta )$
winning for some
$(\alpha ,\beta )$
winning for some
![]() $\alpha ,\beta> 0$
, which is a contradiction.
$\alpha ,\beta> 0$
, which is a contradiction.
Theorem 4.7 may be seen as a quantitative version of the full dimension intersection property of absolute winning sets [Reference Broderick, Fishman, Kleinbock, Reich and Weiss11, Corollary 5.4].
Remark 4.8. In view of Theorem 3.4, if a complete doubling metric space admits a splitting structure
![]() $(X,\mathcal {S},U,f)$
such that
$(X,\mathcal {S},U,f)$
such that
![]() $B=A_\infty (B)$
for every ball B, then the notions of Cantor winning and potential winning sets are equivalent. However, not every metric space X admits such a splitting structure. Indeed, spaces with splitting structures satisfying condition (S4) must have dimensions of the form
$B=A_\infty (B)$
for every ball B, then the notions of Cantor winning and potential winning sets are equivalent. However, not every metric space X admits such a splitting structure. Indeed, spaces with splitting structures satisfying condition (S4) must have dimensions of the form
![]() $({\log n})/({\log m})$
(
$({\log n})/({\log m})$
(
![]() $m,n\in \mathbb {N}$
) (cf. [Reference Badziahin and Harrap5, Theorem 3]), whereas one can construct a complete doubling metric space of arbitrary Hausdorff dimension. In that sense, the notion of potential winning sets is strictly more general than the notion of Cantor winning sets.
$m,n\in \mathbb {N}$
) (cf. [Reference Badziahin and Harrap5, Theorem 3]), whereas one can construct a complete doubling metric space of arbitrary Hausdorff dimension. In that sense, the notion of potential winning sets is strictly more general than the notion of Cantor winning sets.
Remark 4.9. In the above proof, we needed to be careful due to the fact that
![]() $c_0$
potential winning sets are not automatically non-empty (as the winning sets for Schmidt’s game are); indeed, by Proposition 4.6, the empty set is
$c_0$
potential winning sets are not automatically non-empty (as the winning sets for Schmidt’s game are); indeed, by Proposition 4.6, the empty set is
![]() ${\dim _H}(X)$
potential winning.
${\dim _H}(X)$
potential winning.
Lastly, the same observation that is used to prove Proposition 4.6 may be used to prove Theorem 1.16.
Proof of Theorem 1.16
Recall that every closed ball in X of radius
![]() $\leq 1$
is of the form
$\leq 1$
is of the form
whenever
![]() $x\in X$
and
$x\in X$
and
![]() $2^{-n}\leq r < 2^{-n+1}$
. Note that X is 1 Ahlfors regular so it is enough to prove that the exceptional set defined in equation (1), that is,
$2^{-n}\leq r < 2^{-n+1}$
. Note that X is 1 Ahlfors regular so it is enough to prove that the exceptional set defined in equation (1), that is,
is
![]() $\dim _H K$
potential winning. We now define a winning strategy for Alice. Assume Bob chooses
$\dim _H K$
potential winning. We now define a winning strategy for Alice. Assume Bob chooses
![]() $0<\beta <1$
and
$0<\beta <1$
and
![]() $c> \dim _H K$
. Without loss of generality, assume that
$c> \dim _H K$
. Without loss of generality, assume that
![]() $B_0=X$
and
$B_0=X$
and
![]() $r_0=1$
. Then there exists a unique positive integer
$r_0=1$
. Then there exists a unique positive integer
![]() $\ell $
such that
$\ell $
such that
Since
![]() $\dim _H K < c$
, we may choose a collection of open balls
$\dim _H K < c$
, we may choose a collection of open balls
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
![]() $K\subseteq \bigcup _{C\in \mathcal {C}}C$
and
$K\subseteq \bigcup _{C\in \mathcal {C}}C$
and
Let
![]() $\{B_i\}_{i=0}^\infty $
denote any sequence of balls that are chosen by Bob which satisfy
$\{B_i\}_{i=0}^\infty $
denote any sequence of balls that are chosen by Bob which satisfy
![]() $2^{-(i+2)\ell }\leq \mathrm {rad}(B_i) < 2^{-(i+1)\ell }$
. If this sequence is not infinite, then Alice wins by default. By abuse of notation, we will think of
$2^{-(i+2)\ell }\leq \mathrm {rad}(B_i) < 2^{-(i+1)\ell }$
. If this sequence is not infinite, then Alice wins by default. By abuse of notation, we will think of
![]() $B_i$
as Bob’s ith choice, and it will be sufficient to define Alice’s reaction to these moves. On her
$B_i$
as Bob’s ith choice, and it will be sufficient to define Alice’s reaction to these moves. On her
![]() $(i+1)$
st move, Alice will remove the collection
$(i+1)$
st move, Alice will remove the collection
 $$ \begin{align} \mathcal{A}_{i+1}= \bigcup_{j=0}^{\ell-1} \{C : C\in T^{-(i\ell+j)}\mathcal{C} \textrm{ and } C\cap B_i \neq \emptyset\}. \end{align} $$
$$ \begin{align} \mathcal{A}_{i+1}= \bigcup_{j=0}^{\ell-1} \{C : C\in T^{-(i\ell+j)}\mathcal{C} \textrm{ and } C\cap B_i \neq \emptyset\}. \end{align} $$
Here,
![]() $T^{-j} \mathcal {C}$
denotes the set of all images of elements of
$T^{-j} \mathcal {C}$
denotes the set of all images of elements of
![]() $\mathcal {C}$
under the inverse branches of
$\mathcal {C}$
under the inverse branches of
![]() $T^j$
.
$T^j$
.
Note that if Alice still does not win by default, that is, if equation (8) is not satisfied, then necessarily
 $$ \begin{align*} \bigcap_{i=0}^\infty B_i\subseteq \bigg\{x\in X: \{T^i x: i\geq0\}\subseteq X\setminus \bigcup_{C\in\mathcal{C}}C \bigg\} \subseteq E. \end{align*} $$
$$ \begin{align*} \bigcap_{i=0}^\infty B_i\subseteq \bigg\{x\in X: \{T^i x: i\geq0\}\subseteq X\setminus \bigcup_{C\in\mathcal{C}}C \bigg\} \subseteq E. \end{align*} $$
Therefore, we are done once we show that the collection in equation (28) is a legal move for Alice, that is, that it satisfies equation (7). First, for any
![]() $C\in \mathcal {C}$
and
$C\in \mathcal {C}$
and
![]() $j = 0,\ldots ,\ell -1$
, we have that
$j = 0,\ldots ,\ell -1$
, we have that
![]() $T^{-(i\ell +j)}(\{C\})$
is a collection of balls of radius
$T^{-(i\ell +j)}(\{C\})$
is a collection of balls of radius
![]() $2^{-(i\ell +j)}\mathrm {rad}(C)$
, pairwise separated by distances of at least
$2^{-(i\ell +j)}\mathrm {rad}(C)$
, pairwise separated by distances of at least
![]() $2^{-(i\ell +j)} \geq 2^{-i\ell - \ell }$
. Since
$2^{-(i\ell +j)} \geq 2^{-i\ell - \ell }$
. Since
![]() $\mathrm {rad}(B_i) < 2^{-i\ell -\ell }$
, at most one of them intersects
$\mathrm {rad}(B_i) < 2^{-i\ell -\ell }$
, at most one of them intersects
![]() $B_i$
. Therefore,
$B_i$
. Therefore,
 $$ \begin{align*} \sum_{C\in\mathcal{A}_{i+1}} \mathrm{rad}(C)^c \leq \sum_{j=0}^{\ell-1} \sum_{C\in\mathcal{C}}(2^{-(i\ell+j)}\cdot\mathrm{rad}(C))^c \leq \ell 2^{2c\ell} \sum_{C\in\mathcal{C}}\mathrm{rad}(C)^c\cdot \mathrm{rad}(B_i)^c, \end{align*} $$
$$ \begin{align*} \sum_{C\in\mathcal{A}_{i+1}} \mathrm{rad}(C)^c \leq \sum_{j=0}^{\ell-1} \sum_{C\in\mathcal{C}}(2^{-(i\ell+j)}\cdot\mathrm{rad}(C))^c \leq \ell 2^{2c\ell} \sum_{C\in\mathcal{C}}\mathrm{rad}(C)^c\cdot \mathrm{rad}(B_i)^c, \end{align*} $$
which is smaller than
![]() $(\beta \cdot \mathrm {rad}(B_i))^c$
by equation (27).
$(\beta \cdot \mathrm {rad}(B_i))^c$
by equation (27).
5. Counterexamples
The original papers of Schmidt [Reference Schmidt37, Theorem 5] and McMullen [Reference McMullen33] provide examples of sets that are winning (respectively, strong winning) but not absolute winning. We provide two additional counterexamples.
5.1. Cantor winning but not winning
We give an explicit example of a set which is potential winning in
![]() $\mathbb {R}$
(or equivalently, by Theorem 1.5, is Cantor winning), but is not winning. In fact, we will prove more by showing that the set in question is not weak winning (see §2.4).
$\mathbb {R}$
(or equivalently, by Theorem 1.5, is Cantor winning), but is not winning. In fact, we will prove more by showing that the set in question is not weak winning (see §2.4).
Proof of Theorem 1.7
By an iterated function system on
![]() $\mathbb {R}$
, or IFS, we mean a finite collection
$\mathbb {R}$
, or IFS, we mean a finite collection
![]() $\{f_i\;:\mathbb {R}\to \mathbb {R}\}$
,
$\{f_i\;:\mathbb {R}\to \mathbb {R}\}$
,
![]() $i = 1,2,\ldots , N,$
of contracting similarities. By the limit set of the IFS, we mean the unique compact set S which is equal to the union of its images
$i = 1,2,\ldots , N,$
of contracting similarities. By the limit set of the IFS, we mean the unique compact set S which is equal to the union of its images
![]() $f_i(S)$
under the elements of the IFS. We call an IFS on
$f_i(S)$
under the elements of the IFS. We call an IFS on
![]() $\mathbb R$
rational if its elements all preserve the set of rationals. Note that there are only countably many rational IFS.
$\mathbb R$
rational if its elements all preserve the set of rationals. Note that there are only countably many rational IFS.
Let
![]() $E \subseteq \mathbb {R}$
be the complement of the union of the limit sets of all rational IFS whose limit sets have Hausdorff dimension
$E \subseteq \mathbb {R}$
be the complement of the union of the limit sets of all rational IFS whose limit sets have Hausdorff dimension
![]() $\leq 1/2$
. We will show that E is not winning for Schmidt’s game. However, since
$\leq 1/2$
. We will show that E is not winning for Schmidt’s game. However, since
![]() $\dim (\mathbb {R} \setminus E) = 1/2 < 1$
, it follows from Proposition 4.6 that E is
$\dim (\mathbb {R} \setminus E) = 1/2 < 1$
, it follows from Proposition 4.6 that E is
![]() $1/2$
potential winning.
$1/2$
potential winning.
Fix
![]() $\alpha> 0$
and let
$\alpha> 0$
and let
![]() $\beta> 0$
be a small number, to be determined later. We will show that Alice cannot win the weak
$\beta> 0$
be a small number, to be determined later. We will show that Alice cannot win the weak
![]() $(\alpha , \beta )$
game. Let I be a rational interval contained in Alice’s first move, whose length is at least half of the length of Alice’s first move. Without loss of generality, suppose that
$(\alpha , \beta )$
game. Let I be a rational interval contained in Alice’s first move, whose length is at least half of the length of Alice’s first move. Without loss of generality, suppose that
![]() $I = [-1, 1]$
. Let
$I = [-1, 1]$
. Let
![]() $\unicode{x3bb} < 1$
be a rational number large enough so that
$\unicode{x3bb} < 1$
be a rational number large enough so that
![]() $\unicode{x3bb} + \unicode{x3bb} \alpha \geq 1$
, and let
$\unicode{x3bb} + \unicode{x3bb} \alpha \geq 1$
, and let
![]() $\gamma> 0$
be a rational number small enough so that
$\gamma> 0$
be a rational number small enough so that
Consider the IFS on the interval I consisting of the following three contractions:
and note that the condition in equation (29) guarantees that the dimension of the limit set of this IFS is at most
![]() $1/2$
(see, for example, [Reference Hutchinson30, §5.3, Theorem 1]). Bob’s strategy is as follows: on any given turn k, if Alice just made the move
$1/2$
(see, for example, [Reference Hutchinson30, §5.3, Theorem 1]). Bob’s strategy is as follows: on any given turn k, if Alice just made the move
![]() $A_k$
, then find the largest interval
$A_k$
, then find the largest interval
![]() $J_k \subseteq A_k$
which can be written as the image of I under a composition of elements of the IFS, and select the unique ball
$J_k \subseteq A_k$
which can be written as the image of I under a composition of elements of the IFS, and select the unique ball
![]() $B_k$
of radius
$B_k$
of radius
![]() $\beta \cdot \mathrm {rad}(A_{k})$
whose center is the midpoint of this interval. We will show by induction that
$\beta \cdot \mathrm {rad}(A_{k})$
whose center is the midpoint of this interval. We will show by induction that
![]() $B_k \subseteq J_k$
, thus proving that this choice is legal. Indeed, suppose that this holds for k. By ‘blowing up the picture’ using inverse images of the elements of the IFS, we may without loss of generality suppose that
$B_k \subseteq J_k$
, thus proving that this choice is legal. Indeed, suppose that this holds for k. By ‘blowing up the picture’ using inverse images of the elements of the IFS, we may without loss of generality suppose that
![]() $J_k = I$
. Then we have
$J_k = I$
. Then we have
![]() $B_k = [-r, r]$
, where
$B_k = [-r, r]$
, where
![]() $r = \mathrm {rad}(B_k) \leq 1$
. By ‘blowing up the picture’ further using an iterate of the inverse image of the contraction
$r = \mathrm {rad}(B_k) \leq 1$
. By ‘blowing up the picture’ further using an iterate of the inverse image of the contraction
![]() $u_0$
, we may assume without loss of generality that
$u_0$
, we may assume without loss of generality that
![]() $r> \unicode{x3bb} $
. Then Alice’s next choice
$r> \unicode{x3bb} $
. Then Alice’s next choice
![]() $A_{k+1}$
is an interval of length at least
$A_{k+1}$
is an interval of length at least
![]() $2\unicode{x3bb} \alpha $
contained in
$2\unicode{x3bb} \alpha $
contained in
![]() $[-1, 1]$
. However, the set
$[-1, 1]$
. However, the set
![]() $\{\pm \unicode{x3bb} ^q: q = 1, 2, \ldots , N \}$
intersects every interval of length
$\{\pm \unicode{x3bb} ^q: q = 1, 2, \ldots , N \}$
intersects every interval of length
![]() $1 - \unicode{x3bb} $
contained in
$1 - \unicode{x3bb} $
contained in
![]() $[-1, 1]$
, where N is a large constant. Since
$[-1, 1]$
, where N is a large constant. Since
![]() $\unicode{x3bb} \alpha \geq 1-\unicode{x3bb} $
by assumption, there exist
$\unicode{x3bb} \alpha \geq 1-\unicode{x3bb} $
by assumption, there exist
![]() $q \in \{1, \ldots , N\}$
and
$q \in \{1, \ldots , N\}$
and
![]() $\varepsilon \in \{-1,1\}$
such that
$\varepsilon \in \{-1,1\}$
such that
![]() $\varepsilon \unicode{x3bb} ^q \in \tfrac 12 A_{k+1}$
. However, then
$\varepsilon \unicode{x3bb} ^q \in \tfrac 12 A_{k+1}$
. However, then
![]() $J = u^q_0u_{\varepsilon }(I)$
is an interval coming from a cylinder in the IFS construction which intersects
$J = u^q_0u_{\varepsilon }(I)$
is an interval coming from a cylinder in the IFS construction which intersects
![]() $\tfrac 12 A_{k+1}$
, and whose length is
$\tfrac 12 A_{k+1}$
, and whose length is
![]() $2\gamma \unicode{x3bb} ^q \in [2\unicode{x3bb} ^N\gamma , 2\unicode{x3bb} \gamma ]$
. By choosing
$2\gamma \unicode{x3bb} ^q \in [2\unicode{x3bb} ^N\gamma , 2\unicode{x3bb} \gamma ]$
. By choosing
![]() $\gamma \leq \tfrac 14\alpha $
, we can guarantee that the length of J satisfies
$\gamma \leq \tfrac 14\alpha $
, we can guarantee that the length of J satisfies
![]() $2\mathrm {rad}(J) \leq \tfrac 12\unicode{x3bb} \alpha \leq \tfrac 12 \mathrm {rad}(A_{k+1})$
. Combining with the fact that
$2\mathrm {rad}(J) \leq \tfrac 12\unicode{x3bb} \alpha \leq \tfrac 12 \mathrm {rad}(A_{k+1})$
. Combining with the fact that
![]() $J\cap \tfrac 12 A_{k+1} \neq \emptyset $
shows that
$J\cap \tfrac 12 A_{k+1} \neq \emptyset $
shows that
![]() $J\subseteq A_{k+1}$
. So then by the definition of
$J\subseteq A_{k+1}$
. So then by the definition of
![]() $J_{k+1}$
, we have
$J_{k+1}$
, we have
![]() $2\mathrm {rad}(J_{k+1}) \geq 2\mathrm {rad}(J) \geq 2\unicode{x3bb} ^N\gamma $
, and thus by letting
$2\mathrm {rad}(J_{k+1}) \geq 2\mathrm {rad}(J) \geq 2\unicode{x3bb} ^N\gamma $
, and thus by letting
![]() $\beta = \unicode{x3bb} ^N\gamma $
, we get
$\beta = \unicode{x3bb} ^N\gamma $
, we get
![]() $B_{k+1} \subseteq J_{k+1}$
, completing the induction step.
$B_{k+1} \subseteq J_{k+1}$
, completing the induction step.
5.2. Winning but not Cantor winning
Finally, we will show that there exists a set in
![]() $\mathbb {R}$
which is winning, but is not potential winning (or equivalently, by Theorem 1.5, Cantor winning).
$\mathbb {R}$
which is winning, but is not potential winning (or equivalently, by Theorem 1.5, Cantor winning).
Remark 5.1. The above statement remains true if ‘winning’ is replaced by ‘weak winning’, but the resulting statement is weaker and so we prove the original (stronger) statement instead. We will however need the weak
![]() $(\alpha ,\beta )$
game in the proof. It appears that this is a non-trivial application of the weak game.
$(\alpha ,\beta )$
game in the proof. It appears that this is a non-trivial application of the weak game.
By Corollary 3.9, it suffices to show that there exists a winning set E whose complement is weak winning. Note that this also shows that the weak game does not have the intersection property (W2), since E and its complement are both weak winning, but their intersection is empty, and the empty set is not weak winning. We will use the result below as a substitute for the intersection property.
Definition 5.2. A set E is finitely weak winning if Alice can play the weak game so as to guarantee that after finitely many moves, her ball
![]() $A_n$
is a subset of E.
$A_n$
is a subset of E.
Lemma 5.3. The intersection of countably many finitely weak
![]() $\alpha $
winning sets is weak
$\alpha $
winning sets is weak
![]() $\alpha $
winning.
$\alpha $
winning.
Proof. Let
![]() $(E_n)_{n\in \mathbb {N}}$
be a countable collection of finitely weak
$(E_n)_{n\in \mathbb {N}}$
be a countable collection of finitely weak
![]() $\alpha $
winning sets. Alice can use the following strategy to ensure that
$\alpha $
winning sets. Alice can use the following strategy to ensure that
![]() $\bigcap _{m=0}^\infty B_m$
lies inside
$\bigcap _{m=0}^\infty B_m$
lies inside
![]() $\bigcap _{n=0}^\infty E_n$
. She starts by following the strategy to ensure that
$\bigcap _{n=0}^\infty E_n$
. She starts by following the strategy to ensure that
![]() $A_{m_1} \subseteq E_1$
. After that, she starts playing the weak winning game for the set
$A_{m_1} \subseteq E_1$
. After that, she starts playing the weak winning game for the set
![]() $E_2$
, assuming that Bob’s initial move is
$E_2$
, assuming that Bob’s initial move is
![]() $B_{m_1}$
. Therefore, she can ensure that
$B_{m_1}$
. Therefore, she can ensure that
![]() $A_{m_1+m_2} \subseteq E_1\cap E_2$
. Then she switches her strategy to
$A_{m_1+m_2} \subseteq E_1\cap E_2$
. Then she switches her strategy to
![]() $E_3$
and so on.
$E_3$
and so on.
Finally, we have that for any N,
 $$ \begin{align*} \bigcap_{m=1}^\infty A_m \subseteq A_{\sum_{k=1}^N m_k}\subseteq \bigcap_{n=1}^N E_n. \end{align*} $$
$$ \begin{align*} \bigcap_{m=1}^\infty A_m \subseteq A_{\sum_{k=1}^N m_k}\subseteq \bigcap_{n=1}^N E_n. \end{align*} $$
By letting N tend to infinity, we prove the lemma.
In what follows, the intersection of countably many finitely weak
![]() $\alpha $
-winning sets will be called
$\alpha $
-winning sets will be called
![]() $\sigma $
finitely weak
$\sigma $
finitely weak
![]() $\alpha $
-winning.
$\alpha $
-winning.
Proof of Theorem 1.8
Throughout this proof, we let
![]() $Z = \{0,1\}$
and we let
$Z = \{0,1\}$
and we let
![]() $\pi $
denote the coding map for the binary expansion, so that
$\pi $
denote the coding map for the binary expansion, so that
![]() $\pi :Z^{\mathbb {N}}\to [0,1]$
.
$\pi :Z^{\mathbb {N}}\to [0,1]$
.
Definition 5.4. A Bohr set is a set of the form
where
![]() $\gamma ,\delta> 0$
.
$\gamma ,\delta> 0$
.
For each
![]() $\omega = (\omega _n)_{n\in \mathbb {N}}\in Z^{\mathbb {N}}$
, we let
$\omega = (\omega _n)_{n\in \mathbb {N}}\in Z^{\mathbb {N}}$
, we let
![]() $E(\omega ) = \{n\in \mathbb {N} : \omega _n = 1\}$
.
$E(\omega ) = \{n\in \mathbb {N} : \omega _n = 1\}$
.
We now define the set
![]() $E \subseteq \mathbb {R}$
:
$E \subseteq \mathbb {R}$
:
 $$ \begin{align*} E_0: &= \mathbb{Z} + \{\pi(\omega) : \omega\in Z^{\mathbb{N}},\; E(\omega)\text{ contains a Bohr set}\}\\ E: &= \bigcup_{r\in \mathbb{Q}} r E_0. \end{align*} $$
$$ \begin{align*} E_0: &= \mathbb{Z} + \{\pi(\omega) : \omega\in Z^{\mathbb{N}},\; E(\omega)\text{ contains a Bohr set}\}\\ E: &= \bigcup_{r\in \mathbb{Q}} r E_0. \end{align*} $$
We claim that E is
![]() $1/3$
winning, but that its complement is weak
$1/3$
winning, but that its complement is weak
![]() $1/3$
winning.
$1/3$
winning.
Fix
![]() $1/4<\alpha < 1/3$
and
$1/4<\alpha < 1/3$
and
![]() $\beta ,\rho _0> 0$
. We show that Alice has a strategy to win the
$\beta ,\rho _0> 0$
. We show that Alice has a strategy to win the
![]() $(\alpha ,\beta )$
Schmidt game assuming that Bob has chosen a ball of radius
$(\alpha ,\beta )$
Schmidt game assuming that Bob has chosen a ball of radius
![]() $\rho _0$
with his first move. Choose
$\rho _0$
with his first move. Choose
![]() $0 < r\in \mathbb {Q}$
so that
$0 < r\in \mathbb {Q}$
so that
![]() $3 < 2\rho _0/r < \alpha ^{-1}$
, and consider the set
$3 < 2\rho _0/r < \alpha ^{-1}$
, and consider the set
The bounds on
![]() $\alpha $
guarantee that the values
$\alpha $
guarantee that the values
![]() $m_n$
for all
$m_n$
for all
![]() $n\in A$
are distinct. By taking logarithms and rearranging the expression for the set A, we get
$n\in A$
are distinct. By taking logarithms and rearranging the expression for the set A, we get
 $$ \begin{align*} n\in A &\Leftrightarrow \text{ there exists } m \;\; \log 3 <(n+1)\log 2 + m\log(\alpha\beta) + \log(\rho_0/r) < \log (\alpha^{-1})\\ &\Leftrightarrow n \frac{\log 2}{-\log(\alpha\beta)} \in \bigg( \frac{\log ({3}/{2\rho_0/r})}{-\log(\alpha\beta)} , \frac{\log ({\alpha^{-1}}/{2\rho_0/r})}{-\log(\alpha\beta)} \bigg) \text{ mod 1}. \end{align*} $$
$$ \begin{align*} n\in A &\Leftrightarrow \text{ there exists } m \;\; \log 3 <(n+1)\log 2 + m\log(\alpha\beta) + \log(\rho_0/r) < \log (\alpha^{-1})\\ &\Leftrightarrow n \frac{\log 2}{-\log(\alpha\beta)} \in \bigg( \frac{\log ({3}/{2\rho_0/r})}{-\log(\alpha\beta)} , \frac{\log ({\alpha^{-1}}/{2\rho_0/r})}{-\log(\alpha\beta)} \bigg) \text{ mod 1}. \end{align*} $$
Since the interval on the right-hand side contains 0, this implies that A contains a Bohr set.
Now fix
![]() $n\in A$
and let
$n\in A$
and let
![]() $m = m_n \in \mathbb {N}$
be the corresponding value. On the mth turn, Bob’s interval
$m = m_n \in \mathbb {N}$
be the corresponding value. On the mth turn, Bob’s interval
![]() $B_m$
is of length
$B_m$
is of length
![]() $2(\alpha \beta )^m \rho _0 \geq 3\cdot 2^{-n} r$
, so if we subdivide
$2(\alpha \beta )^m \rho _0 \geq 3\cdot 2^{-n} r$
, so if we subdivide
![]() $\mathbb {R}$
into intervals of length
$\mathbb {R}$
into intervals of length
![]() $2^{-n} r$
, then
$2^{-n} r$
, then
![]() $B_m$
must contain at least two of them. Since Alice’s next interval is of length
$B_m$
must contain at least two of them. Since Alice’s next interval is of length
![]() $2\alpha (\alpha \beta )^m \rho _0 \leq 2^{-n} r$
, this means that Alice can choose a subinterval of either one of these intervals on her turn. So Alice can control the nth binary digit of
$2\alpha (\alpha \beta )^m \rho _0 \leq 2^{-n} r$
, this means that Alice can choose a subinterval of either one of these intervals on her turn. So Alice can control the nth binary digit of
![]() $x/r$
, where x is the outcome of the game, and, in particular, she can set the nth digit to
$x/r$
, where x is the outcome of the game, and, in particular, she can set the nth digit to
![]() $1$
. Since every value m corresponds to only one value
$1$
. Since every value m corresponds to only one value
![]() $n\in A$
, Alice can set all of the digits of
$n\in A$
, Alice can set all of the digits of
![]() $x/r$
whose indices are in A to
$x/r$
whose indices are in A to
![]() $1$
. This means that
$1$
. This means that
![]() $x/r\in E_0$
and thus
$x/r\in E_0$
and thus
![]() $x\in E$
, so Alice can force the outcome of the game to lie in E. So by Proposition 1.2, E is
$x\in E$
, so Alice can force the outcome of the game to lie in E. So by Proposition 1.2, E is
![]() $1/3$
winning.
$1/3$
winning.
Now if we show that
![]() $\mathbb {R}\setminus E_0$
is
$\mathbb {R}\setminus E_0$
is
![]() $\sigma $
finitely weak
$\sigma $
finitely weak
![]() $1/3$
winning, then by symmetry,
$1/3$
winning, then by symmetry,
![]() $\mathbb {R}\setminus rE_0$
is
$\mathbb {R}\setminus rE_0$
is
![]() $\sigma $
finitely weak
$\sigma $
finitely weak
![]() $1/3$
winning for all
$1/3$
winning for all
![]() $r> 0$
, and since the intersection of countably many
$r> 0$
, and since the intersection of countably many
![]() $\sigma $
finitely weak
$\sigma $
finitely weak
![]() $1/3$
winning sets is
$1/3$
winning sets is
![]() $\sigma $
finitely weak
$\sigma $
finitely weak
![]() $1/3$
winning, it follows that
$1/3$
winning, it follows that
![]() $\mathbb {R}\setminus E$
is
$\mathbb {R}\setminus E$
is
![]() $\sigma $
finitely weak
$\sigma $
finitely weak
![]() $1/3$
winning. By symmetry, it suffices to consider the case
$1/3$
winning. By symmetry, it suffices to consider the case
![]() $r=1$
. To prove that
$r=1$
. To prove that
![]() $\mathbb {R}\setminus E_0$
is indeed
$\mathbb {R}\setminus E_0$
is indeed
![]() $\sigma $
finitely weak
$\sigma $
finitely weak
![]() $1/3$
winning, we will use the following lemma.
$1/3$
winning, we will use the following lemma.
Lemma 5.5. Fix
![]() $0 < \alpha < 1/3$
and
$0 < \alpha < 1/3$
and
![]() $\beta> 0$
. Then there exists
$\beta> 0$
. Then there exists
![]() $N\in \mathbb {N}$
such that for any
$N\in \mathbb {N}$
such that for any
![]() $\rho _0> 0$
, there exists
$\rho _0> 0$
, there exists
![]() $a_1(\rho _0)$
so that for any sequence of integers
$a_1(\rho _0)$
so that for any sequence of integers
![]() $(a_k)_{1\leqslant k\leqslant M}$
with
$(a_k)_{1\leqslant k\leqslant M}$
with
Alice has a strategy in the finite weak
![]() $(\alpha ,\beta )$
game to control the digits indexed by the integers
$(\alpha ,\beta )$
game to control the digits indexed by the integers
![]() $(a_k)_{1\leqslant k\leqslant M}$
.
$(a_k)_{1\leqslant k\leqslant M}$
.
Proof of Lemma 5.5
Suppose that Bob has just played a move of radius
![]() $\rho $
. Then Alice can play any radius between
$\rho $
. Then Alice can play any radius between
![]() $\alpha \rho $
and
$\alpha \rho $
and
![]() $\rho $
, forcing Bob to play a predetermined radius between
$\rho $
, forcing Bob to play a predetermined radius between
![]() $\alpha \beta \rho $
and
$\alpha \beta \rho $
and
![]() $\beta \rho $
. After iterating n times, Alice can force Bob to play a ball of any given radius between
$\beta \rho $
. After iterating n times, Alice can force Bob to play a ball of any given radius between
![]() $\alpha ^n \beta ^n \rho $
and
$\alpha ^n \beta ^n \rho $
and
![]() $\beta ^n\rho $
. Since
$\beta ^n\rho $
. Since
![]() $\alpha ^n < \beta $
for sufficiently large n, there exists
$\alpha ^n < \beta $
for sufficiently large n, there exists
![]() $\gamma> 0$
such that Alice can force Bob to play a ball of any prescribed radius
$\gamma> 0$
such that Alice can force Bob to play a ball of any prescribed radius
![]() $\leq \gamma \rho $
(after a sufficient number of turns depending on the radius). Now Alice uses the following strategy: for each
$\leq \gamma \rho $
(after a sufficient number of turns depending on the radius). Now Alice uses the following strategy: for each
![]() $k = 1,\ldots ,M$
, first force Bob to play a ball whose radius is
$k = 1,\ldots ,M$
, first force Bob to play a ball whose radius is
![]() $3 \cdot 2^{-a_k}$
, and then respond to Bob’s choice in a way such that the
$3 \cdot 2^{-a_k}$
, and then respond to Bob’s choice in a way such that the
![]() $a_k$
th digit of the outcome is guaranteed (this is possible by the argument from the previous proof). Forcing Bob to play these radii is possible as long as
$a_k$
th digit of the outcome is guaranteed (this is possible by the argument from the previous proof). Forcing Bob to play these radii is possible as long as
![]() $3\cdot 2^{-a_1} \leq \gamma \rho _0$
and
$3\cdot 2^{-a_1} \leq \gamma \rho _0$
and
![]() $3\cdot 2^{-a_{k+1}} \leq \gamma \alpha 3 \cdot 2^{-a_k}$
for all k. By equation (30), the latter statement is true as long as N and
$3\cdot 2^{-a_{k+1}} \leq \gamma \alpha 3 \cdot 2^{-a_k}$
for all k. By equation (30), the latter statement is true as long as N and
![]() $a_1(\rho _0)$
are sufficiently large.
$a_1(\rho _0)$
are sufficiently large.
To continue the proof of Theorem 1.8, fix
![]() $0 < \alpha < 1/3$
and
$0 < \alpha < 1/3$
and
![]() $\beta> 0$
, and let
$\beta> 0$
, and let
![]() $N\in \mathbb {N}$
be as in Lemma 5.5. Then we get the following.
$N\in \mathbb {N}$
be as in Lemma 5.5. Then we get the following.
-
• For all
 $k\in \mathbb {N}$
, the set is finitely weak winning, where
$k\in \mathbb {N}$
, the set is finitely weak winning, where $$ \begin{align*} A_k:= \mathbb{Z} + \{\pi(\omega) : T(\omega) \text{ contains an arithmetic progression of length } k \text{ and gap size } N\} \end{align*} $$
$$ \begin{align*} A_k:= \mathbb{Z} + \{\pi(\omega) : T(\omega) \text{ contains an arithmetic progression of length } k \text{ and gap size } N\} \end{align*} $$
 $T(\omega ) := \mathbb {N}\setminus E(\omega ) = \{n\in \mathbb {N}: \omega _n=0\}$
.
$T(\omega ) := \mathbb {N}\setminus E(\omega ) = \{n\in \mathbb {N}: \omega _n=0\}$
.
-
• For all
 $q,i\in \mathbb {N}$
, the set is finitely weak winning.
$q,i\in \mathbb {N}$
, the set is finitely weak winning. $$ \begin{align*} A_{q,i} := \mathbb{Z} + \{\pi(\omega) : T(\omega) \cap (q\mathbb{N} + i) \neq \emptyset\} \end{align*} $$
$$ \begin{align*} A_{q,i} := \mathbb{Z} + \{\pi(\omega) : T(\omega) \cap (q\mathbb{N} + i) \neq \emptyset\} \end{align*} $$
So the intersection
 $$ \begin{align*} A = \bigcap_k A_k \cap \bigcap_{q,i} A_{q,i} \end{align*} $$
$$ \begin{align*} A = \bigcap_k A_k \cap \bigcap_{q,i} A_{q,i} \end{align*} $$
is
![]() $\sigma $
finitely weak winning. To finish the proof, we need to show that
$\sigma $
finitely weak winning. To finish the proof, we need to show that
![]() $\mathbb {R}\setminus E_0 \supseteq A$
. Indeed, fix
$\mathbb {R}\setminus E_0 \supseteq A$
. Indeed, fix
![]() $n + \pi (\omega ) \in A$
. Then
$n + \pi (\omega ) \in A$
. Then
![]() $T(\omega )$
contains arbitrarily long arithmetic progressions of gap size N, and intersects every infinite arithmetic progression non-trivially.
$T(\omega )$
contains arbitrarily long arithmetic progressions of gap size N, and intersects every infinite arithmetic progression non-trivially.
Now let
![]() $A(\gamma ,\delta )$
be a Bohr set, and we will show that
$A(\gamma ,\delta )$
be a Bohr set, and we will show that
![]() $A(\gamma ,\delta )$
intersects
$A(\gamma ,\delta )$
intersects
![]() $T(\omega )$
non-trivially. First suppose that
$T(\omega )$
non-trivially. First suppose that
![]() $\gamma $
is irrational. Then so is
$\gamma $
is irrational. Then so is
![]() $N\gamma $
, so by the minimality of irrational rotations, there exists M such that the finite sequence
$N\gamma $
, so by the minimality of irrational rotations, there exists M such that the finite sequence
![]() $0,N\gamma ,\ldots ,MN\gamma $
is
$0,N\gamma ,\ldots ,MN\gamma $
is
![]() $\delta $
-dense in
$\delta $
-dense in
![]() $\mathbb {R}/\mathbb {Z}$
. Now let
$\mathbb {R}/\mathbb {Z}$
. Now let
![]() $n,n+N,\ldots ,n+MN$
be an arithmetic progression of length M and gap size N contained in
$n,n+N,\ldots ,n+MN$
be an arithmetic progression of length M and gap size N contained in
![]() $T(\omega )$
. Then
$T(\omega )$
. Then
![]() $n\gamma ,n\gamma + N\gamma ,\ldots ,n\gamma + MN\gamma $
is also
$n\gamma ,n\gamma + N\gamma ,\ldots ,n\gamma + MN\gamma $
is also
![]() $\delta $
-dense in
$\delta $
-dense in
![]() $\mathbb {R}/\mathbb {Z}$
and, in particular, must contain an element of
$\mathbb {R}/\mathbb {Z}$
and, in particular, must contain an element of
![]() $(-\delta ,\delta )$
. So
$(-\delta ,\delta )$
. So
![]() $(n+iN)\gamma \in (-\delta ,\delta )$
mod 1 for some
$(n+iN)\gamma \in (-\delta ,\delta )$
mod 1 for some
![]() $i = 0,\ldots ,M$
. However, then
$i = 0,\ldots ,M$
. However, then
![]() $n+iN \in A(\gamma ,\delta ) \cap T(\omega )$
.
$n+iN \in A(\gamma ,\delta ) \cap T(\omega )$
.
Alternatively, suppose that
![]() $\gamma $
is rational, say
$\gamma $
is rational, say
![]() $\gamma = p/q$
. Then
$\gamma = p/q$
. Then
![]() $A(\gamma ,\delta )$
contains the infinite arithmetic progression
$A(\gamma ,\delta )$
contains the infinite arithmetic progression
![]() $q\mathbb {N}$
, which by assumption intersects
$q\mathbb {N}$
, which by assumption intersects
![]() $T(\omega )$
non-trivially.
$T(\omega )$
non-trivially.
Thus, every Bohr set intersects
![]() $T(\omega )$
non-trivially, so
$T(\omega )$
non-trivially, so
![]() $E(\omega )$
does not contain any Bohr set, that is,
$E(\omega )$
does not contain any Bohr set, that is,
![]() $n + \pi (\omega ) \notin E_0$
. So
$n + \pi (\omega ) \notin E_0$
. So
![]() $A \subseteq \mathbb {R}\setminus E_0$
, completing the proof.
$A \subseteq \mathbb {R}\setminus E_0$
, completing the proof.
Acknowledgements
E.N. and D.S. were supported by EPSRC Programme Grant: EP/J018260/1. E.N. wishes to thank Dmitry Dolgopyat for suggesting to use games to prove [Reference Dolgopyat17, Theorem 1] during the 2016 ‘Dimension and Dynamics’ semester at ICERM.