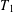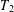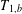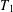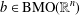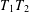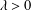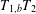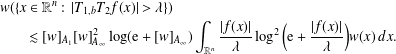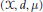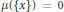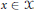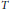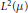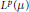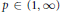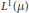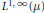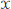Let 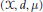 $\left( \text{ }\!\!\chi\!\!\text{ ,}\,d,\,\mu \right)$ be a separable metric measure space satisfying the known upper doubling condition, the geometrical doubling condition, and the non-atomic condition that
$\left( \text{ }\!\!\chi\!\!\text{ ,}\,d,\,\mu \right)$ be a separable metric measure space satisfying the known upper doubling condition, the geometrical doubling condition, and the non-atomic condition that 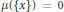 $\mu \left( \left\{ x \right\} \right)\,=\,0$ for all
$\mu \left( \left\{ x \right\} \right)\,=\,0$ for all 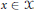 $x\,\in \,\text{ }\!\!\chi\!\!\text{ }$. In this paper, we show that the boundedness of a Calderón–Zygmund operator
$x\,\in \,\text{ }\!\!\chi\!\!\text{ }$. In this paper, we show that the boundedness of a Calderón–Zygmund operator 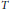 $T$ on
$T$ on 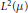 ${{L}^{2}}\left( \mu \right)$ is equivalent to that of
${{L}^{2}}\left( \mu \right)$ is equivalent to that of 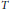 $T$ on
$T$ on 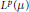 ${{L}^{p}}\left( \mu \right)$ for some
${{L}^{p}}\left( \mu \right)$ for some 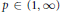 $p\,\in \,\left( 1,\,\infty \right)$, and that of
$p\,\in \,\left( 1,\,\infty \right)$, and that of 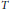 $T$ from
$T$ from 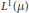 ${{L}^{1}}\left( \mu \right)$ to
${{L}^{1}}\left( \mu \right)$ to 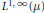 ${{L}^{1,\,\infty }}\left( \mu \right)$. As an application, we prove that if
${{L}^{1,\,\infty }}\left( \mu \right)$. As an application, we prove that if 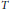 $T$ is a Calderón–Zygmund operator bounded on
$T$ is a Calderón–Zygmund operator bounded on 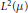 ${{L}^{2}}\left( \mu \right)$, then its maximal operator is bounded on
${{L}^{2}}\left( \mu \right)$, then its maximal operator is bounded on 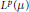 ${{L}^{p}}\left( \mu \right)$ for all
${{L}^{p}}\left( \mu \right)$ for all 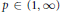 $p\,\in \,\left( 1,\,\infty \right)$ and from the space of all complex-valued Borel measures on
$p\,\in \,\left( 1,\,\infty \right)$ and from the space of all complex-valued Borel measures on 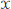 $\text{ }\!\!\chi\!\!\text{ }$ to
$\text{ }\!\!\chi\!\!\text{ }$ to 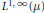 ${{L}^{1,\,\infty }}\left( \mu \right)$. All these results generalize the corresponding results of Nazarov et al. on metric spaces with measures satisfying the so-called polynomial growth condition.
${{L}^{1,\,\infty }}\left( \mu \right)$. All these results generalize the corresponding results of Nazarov et al. on metric spaces with measures satisfying the so-called polynomial growth condition.