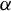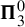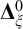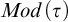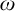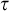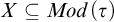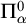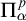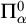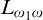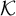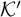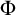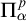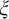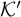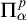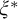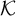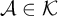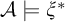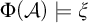We study the descriptive complexity of sets of points defined by restricting the statistical behaviour of their orbits in dynamical systems on Polish spaces. Particular examples of such sets are the sets of generic points of invariant Borel probability measures, but we also consider much more general sets (for example, 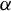$\alpha $-Birkhoff regular sets and the irregular set appearing in the multifractal analysis of ergodic averages of a continuous real-valued function). We show that many of these sets are Borel in general, and all these are Borel when we assume that our space is compact. We provide examples of these sets being non-Borel, properly placed at the first level of the projective hierarchy (they are complete analytic or co-analytic). This proves that the compactness assumption is, in some cases, necessary to obtain Borelness. When these sets are Borel, we measure their descriptive complexity using the Borel hierarchy. We show that the sets of interest are located at most at the third level of the hierarchy. We also use a modified version of the specification property to show that these sets are properly located at the third level of the hierarchy for many dynamical systems. To demonstrate that the specification property is a sufficient, but not necessary, condition for maximal descriptive complexity of a set of generic points, we provide an example of a compact minimal system with an invariant measure whose set of generic points is 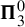$\boldsymbol {\Pi }^0_3$-complete.

We present the true stages machinery and illustrate its applications to descriptive set theory. We use this machinery to provide new proofs of the Hausdorff–Kuratowski and Wadge theorems on the structure of $\mathbf {\Delta }^0_\xi $, Louveau and Saint Raymond’s separation theorem, and Louveau’s separation theorem.

We prove an effective version of the Lopez-Escobar theorem for continuous domains. Let $Mod(\tau )$ be the set of countable structures with universe $\omega $ in vocabulary $\tau $ topologized by the Scott topology. We show that an invariant set $X\subseteq Mod(\tau )$ is $\Pi ^0_\alpha $ in the Borel hierarchy of this topology if and only if it is definable by a $\Pi ^p_\alpha $-formula, a positive $\Pi ^0_\alpha $ formula in the infinitary logic $L_{\omega _1\omega }$. As a corollary of this result we obtain a new pullback theorem for positive computable embeddings: Let $\mathcal {K}$ be positively computably embeddable in $\mathcal {K}'$ by $\Phi $, then for every $\Pi ^p_\alpha $ formula $\xi $ in the vocabulary of $\mathcal {K}'$ there is a $\Pi ^p_\alpha $ formula $\xi ^{*}$ in the vocabulary of $\mathcal {K}$ such that for all $\mathcal {A}\in \mathcal {K}$, $\mathcal {A}\models \xi ^{*}$ if and only if $\Phi (\mathcal {A})\models \xi $. We use this to obtain new results on the possibility of positive computable embeddings into the class of linear orderings.

The Wadge hierarchy was originally defined and studied only in the Baire space (and some other zero-dimensional spaces). Here we extend the Wadge hierarchy of Borel sets to arbitrary topological spaces by providing a set-theoretic definition of all its levels. We show that our extension behaves well in second countable spaces and especially in quasi-Polish spaces. In particular, all levels are preserved by continuous open surjections between second countable spaces which implies e.g., several Hausdorff–Kuratowski (HK)-type theorems in quasi-Polish spaces. In fact, many results hold not only for the Wadge hierarchy of sets but also for its extension to Borel functions from a space to a countable better quasiorder Q.