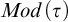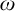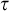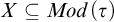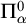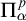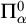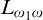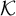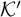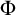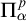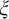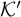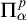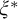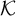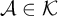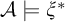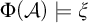1 Introduction
A common theme in the study of countable mathematical structures is that isomorphism invariant properties have syntactic characterizations. Examples of this phenomenon are the existence of Scott sentences for countable structures [Reference Scott30], the Lopez-Escobar theorem, which says that every invariant Borel subset in the space of countable structures is definable in the infinitary logic
![]() $L_{\omega _1\omega }$
[Reference Lopez-Escobar24], or that a relation on a structure that is
$L_{\omega _1\omega }$
[Reference Lopez-Escobar24], or that a relation on a structure that is
![]() $\Sigma ^0_\alpha $
in every copy is definable by a computable
$\Sigma ^0_\alpha $
in every copy is definable by a computable
![]() $\Sigma ^0_\alpha $
$\Sigma ^0_\alpha $
![]() $L_{\omega _1\omega }$
-formula [Reference Ash, Knight, Manasse and Slaman2, Reference Chisholm10].
$L_{\omega _1\omega }$
-formula [Reference Ash, Knight, Manasse and Slaman2, Reference Chisholm10].
Definability in the logic
![]() $L_{\omega _1\omega }$
is closely related to Turing reducibility. The base case of [Reference Ash, Knight, Manasse and Slaman2, Reference Chisholm10] tells us that a relation is definable by a computable
$L_{\omega _1\omega }$
is closely related to Turing reducibility. The base case of [Reference Ash, Knight, Manasse and Slaman2, Reference Chisholm10] tells us that a relation is definable by a computable
![]() $\Sigma ^0_1$
formula and a computable
$\Sigma ^0_1$
formula and a computable
![]() $\Pi ^0_1$
formula if and only if it is computable in every copy. Similarly, evaluating whether a computable infinitary
$\Pi ^0_1$
formula if and only if it is computable in every copy. Similarly, evaluating whether a computable infinitary
![]() $\Sigma ^0_\alpha $
formula holds of a structure
$\Sigma ^0_\alpha $
formula holds of a structure
![]() $\mathcal {A}$
is c.e. in the
$\mathcal {A}$
is c.e. in the
![]() $\alpha $
th Turing jump of
$\alpha $
th Turing jump of
![]() $\mathcal {A}$
, and hence deciding membership of computable structures in
$\mathcal {A}$
, and hence deciding membership of computable structures in
![]() $\Sigma ^0_\alpha $
sets is
$\Sigma ^0_\alpha $
sets is
![]() $\Sigma ^0_\alpha $
. Another fact that makes this connection is that the space of countable
$\Sigma ^0_\alpha $
. Another fact that makes this connection is that the space of countable
![]() $\tau $
-structures with universe
$\tau $
-structures with universe
![]() $\omega $
,
$\omega $
,
![]() $Mod(\tau )$
, can be viewed as a closed subspace of Cantor space
$Mod(\tau )$
, can be viewed as a closed subspace of Cantor space
![]() $\mathcal C$
. It is well known that continuous functions
$\mathcal C$
. It is well known that continuous functions
![]() $\mathcal C\to \mathcal C$
are X-computable operators relative to some
$\mathcal C\to \mathcal C$
are X-computable operators relative to some
![]() $X\in 2^\omega $
, and thus Turing computable operators correspond to the effectively continuous functions.
$X\in 2^\omega $
, and thus Turing computable operators correspond to the effectively continuous functions.
Being a powerful tool to study algorithmic properties, Turing reducibility is not well suited to deal with partial objects, such as c.e. sets, partial functions, and partial structures. Enumeration reducibility was introduced by Friedberg and Rogers [Reference Friedberg and Rogers15] as a generalization of relative computability intended to deal with partial objects. Namely,
![]() $X\subseteq \omega $
is enumeration reducible to
$X\subseteq \omega $
is enumeration reducible to
![]() $Y\subseteq \omega $
,
$Y\subseteq \omega $
,
![]() $X\leq _e Y$
, if every enumeration of Y computes an enumeration of X. Given the explained above relationship between definability and Turing computability, one wonders whether a similar relationship can be established between definability and enumeration reducibility. To establish such a correspondence, throughout the paper we will treat structures as partial objects given by their positive diagrams. For a structure
$X\leq _e Y$
, if every enumeration of Y computes an enumeration of X. Given the explained above relationship between definability and Turing computability, one wonders whether a similar relationship can be established between definability and enumeration reducibility. To establish such a correspondence, throughout the paper we will treat structures as partial objects given by their positive diagrams. For a structure
![]() $\mathcal {A}$
in a relational vocabulary
$\mathcal {A}$
in a relational vocabulary
![]() $\tau $
its positive diagram is the set
$\tau $
its positive diagram is the set
![]() $\bigoplus _{R_i\in \tau } R_i^{\mathcal {A}}$
.
$\bigoplus _{R_i\in \tau } R_i^{\mathcal {A}}$
.
Algorithmic properties of structures given by their positive diagrams have been studied for a long time, as this kind of presentation has deep connections to results in algebra and theoretical computer science. The formal general definition of positive (or c.e.) structures was given by Mal’cev [Reference Mal’cev25]. From an algebraic point of view, many finitely presented algebras are naturally positive but lack a computable presentation [Reference Boone5, Reference Markov26, Reference Novikov28]. An extensive overview of results on positive (c.e.) structures from the twentieth century can be found in [Reference Selivanov31]. Later c.e. structures were studied by Harizanov and co-authors [Reference Cenzer, Harizanov and Remmel8, Reference Cenzer, Harizanov and Remmel9, Reference Dimitrov and Harizanov14]. In a recent survey [Reference Khoussainov21] Khoussainov summarizes more results on c.e. structures and suggests new questions, relating the study of c.e. structures to the theory of equivalence relations. Further recent results about c.e. structures could be found, e.g., in [Reference Gavruskin, Jain, Khoussainov and Stephan17, Reference Godziszewski, Hamkins, Kennedy and Queiroz18].
The approach that applies enumeration reducibility to study computational properties of structures goes back to Soskov [Reference Soskov34, Reference Soskov, Baleva, Chatzidakis, Koepke and Pohlers35] who adapted notions studied in computable structure theory to enumeration reducibility. Assuming that a structure is given by its positive diagram, one may ask questions similar to the ones in classic computable structure theory but with respect to enumeration reducibility. For example, Richter introduced the notion of the Turing degree spectrum of a structure, the set of Turing degrees of its isomorphic copies [Reference Richter29]. The first and one of the fundamental results in this area of Knight is a dichotomy [Reference Knight22]. If a structure is automorphically non-trivial, its degree spectrum is upwards closed. Otherwise, it is a singleton. This dichotomy disappears in the analogue of this notion for enumeration reducibility—enumeration degree spectra. The enumeration degree spectrum of a structure is the set of degrees of enumerations of its positive diagram [Reference Soskov34]. Soskov’s work on this notion exposed deep theory and contributed to the study of Turing degree spectra (see [Reference Soskova and Soskova36] for a survey). In [Reference Csima, MacLean and Rossegger12] r.i.p.e. relations, relations that are enumerable from the positive diagrams of all isomorphic copies of a given structure, were studied. The main results show that a relation is r.i.p.e. if and only if it is definable by a positive computable
![]() $\Sigma ^0_1$
infinitary formula, and that positive enumerable functors—a reducibility between structures introduced in [Reference Csima, Rossegger and Yu13]—have a syntactic equivalent in a version of interpretability using
$\Sigma ^0_1$
infinitary formula, and that positive enumerable functors—a reducibility between structures introduced in [Reference Csima, Rossegger and Yu13]—have a syntactic equivalent in a version of interpretability using
![]() $\Sigma ^p_1$
formulas.
$\Sigma ^p_1$
formulas.
In this article, we establish another relationship between definability by positive infinitary formulas and enumeration reducibility. Our main result is an effective version of the Lopez-Escobar theorem that establishes a connection between the Borel hierarchy on the Scott topology on the space of countable structures and a hierarchy of positive
![]() $L_{\omega _1\omega }$
-formulas. Let
$L_{\omega _1\omega }$
-formulas. Let
![]() $(Mod(\tau ), \preceq )$
be the set of countable structures in the relational language
$(Mod(\tau ), \preceq )$
be the set of countable structures in the relational language
![]() $\tau $
with universe
$\tau $
with universe
![]() $\omega $
, where
$\omega $
, where
![]() $\preceq $
is the substructure ordering on
$\preceq $
is the substructure ordering on
![]() $Mod(\tau )$
. This ordering gives rise to a topology, the Scott topology with basic open sets the superstructures of
$Mod(\tau )$
. This ordering gives rise to a topology, the Scott topology with basic open sets the superstructures of
![]() $\tau $
-finite structures. It is not a Polish space but an
$\tau $
-finite structures. It is not a Polish space but an
![]() $\omega $
-continuous domain and allows the definition of a Borel hierarchy. Selivanov [Reference Selivanov33] showed that the Borel sets in this topology equal the Borel sets under the usual Polish topology on
$\omega $
-continuous domain and allows the definition of a Borel hierarchy. Selivanov [Reference Selivanov33] showed that the Borel sets in this topology equal the Borel sets under the usual Polish topology on
![]() $Mod(\tau )$
and, thus, one gets Lopez-Escobar’s theorem for the Scott topology for free. However, the Borel hierarchies on this spaces differ and we will prove a stronger version of this theorem, matching the Borel complexity with the complexity of defining formulas. We show that a set is
$Mod(\tau )$
and, thus, one gets Lopez-Escobar’s theorem for the Scott topology for free. However, the Borel hierarchies on this spaces differ and we will prove a stronger version of this theorem, matching the Borel complexity with the complexity of defining formulas. We show that a set is
![]() $\Pi ^0_\alpha $
in the effective Borel hierarchy on the Scott topology if and only if it is definable by a computable
$\Pi ^0_\alpha $
in the effective Borel hierarchy on the Scott topology if and only if it is definable by a computable
![]() $\Pi ^p_\alpha $
formula (Theorem 3.12). The p in
$\Pi ^p_\alpha $
formula (Theorem 3.12). The p in
![]() $\Pi ^p_\alpha $
stands for positive; the
$\Pi ^p_\alpha $
stands for positive; the
![]() $\Pi ^p_\alpha $
formulas are a subset of the classical
$\Pi ^p_\alpha $
formulas are a subset of the classical
![]() $\Pi ^0_\alpha $
formulas in the logic
$\Pi ^0_\alpha $
formulas in the logic
![]() $L_{\omega _1\omega }$
with the use of negations restricted. Vanden Boom [Reference Vanden Boom4] showed the analogue of our theorem in the classical setting. The bold-face version is a corollary of Vaught’s proof of the Lopez-Escobar theorem [Reference Vaught37]. We will prove our version of the Lopez-Escobar theorem using a notion of forcing which can be seen as an amalgamation of the forcing used in Vanden Boom’s proof and a forcing used by Soskov [Reference Soskov34].
$L_{\omega _1\omega }$
with the use of negations restricted. Vanden Boom [Reference Vanden Boom4] showed the analogue of our theorem in the classical setting. The bold-face version is a corollary of Vaught’s proof of the Lopez-Escobar theorem [Reference Vaught37]. We will prove our version of the Lopez-Escobar theorem using a notion of forcing which can be seen as an amalgamation of the forcing used in Vanden Boom’s proof and a forcing used by Soskov [Reference Soskov34].
As Turing computable operators are to Polish spaces, enumeration operators are to the Scott topology. Enumeration operators can be viewed as functions mapping subsets of
![]() $\omega $
to subsets of
$\omega $
to subsets of
![]() $\omega $
and thus as functions from
$\omega $
and thus as functions from
![]() $2^\omega $
to
$2^\omega $
to
![]() $2^\omega $
. While we have only defined the Scott topology on
$2^\omega $
. While we have only defined the Scott topology on
![]() $Mod(\tau )$
, there is a similar topology on
$Mod(\tau )$
, there is a similar topology on
![]() $2^\omega $
where the basic open sets are the supersets of finite sets. Enumeration operators correspond to effective Scott continuous functions from
$2^\omega $
where the basic open sets are the supersets of finite sets. Enumeration operators correspond to effective Scott continuous functions from
![]() $2^\omega $
to
$2^\omega $
to
![]() $2^\omega $
. As in the classical case, we can view the Scott topology on
$2^\omega $
. As in the classical case, we can view the Scott topology on
![]() $Mod(\tau )$
as a subspace of the Scott topology on
$Mod(\tau )$
as a subspace of the Scott topology on
![]() $2^{\omega }$
. We use this fact to obtain a new pullback theorem for computable embeddings. A computable embedding between two classes
$2^{\omega }$
. We use this fact to obtain a new pullback theorem for computable embeddings. A computable embedding between two classes
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\mathcal {K}'$
is an enumeration operator
$\mathcal {K}'$
is an enumeration operator
![]() $\Phi $
such that for
$\Phi $
such that for
![]() $\mathcal {A}\in \mathcal {K}$
,
$\mathcal {A}\in \mathcal {K}$
,
![]() $\Phi (\mathcal {A})\in K'$
, and
$\Phi (\mathcal {A})\in K'$
, and
![]() $\mathcal {A}\cong \mathcal {B}$
if and only if
$\mathcal {A}\cong \mathcal {B}$
if and only if
![]() $\Phi (\mathcal {A})\cong \Phi (\mathcal {B})$
[Reference Calvert, Cummins, Knight and Miller7]. Our pullback theorem says that for
$\Phi (\mathcal {A})\cong \Phi (\mathcal {B})$
[Reference Calvert, Cummins, Knight and Miller7]. Our pullback theorem says that for
![]() $\xi $
a
$\xi $
a
![]() $\Pi ^p_\alpha $
formula in the vocabulary of
$\Pi ^p_\alpha $
formula in the vocabulary of
![]() $\mathcal {K}'$
, there is
$\mathcal {K}'$
, there is
![]() $\xi ^{*}$
, a
$\xi ^{*}$
, a
![]() $\Pi ^p_\alpha $
formula in the vocabulary of
$\Pi ^p_\alpha $
formula in the vocabulary of
![]() $\mathcal {K}$
such that for all
$\mathcal {K}$
such that for all
![]() $\mathcal {A}\in \mathcal {K}$
,
$\mathcal {A}\in \mathcal {K}$
,
![]() $\mathcal {A}\models \xi ^{*}$
if and only if
$\mathcal {A}\models \xi ^{*}$
if and only if
![]() $\Phi (\mathcal {A})\models \xi $
(Theorem 4.5).
$\Phi (\mathcal {A})\models \xi $
(Theorem 4.5).
Computable embeddings and their classical analogue, Turing computable embeddings [Reference Knight, Miller and Vanden Boom23], have been heavily studied in computable structure theory over the last decade. One question that has seen interest is to find a dividing line between these two types of reducibilities [Reference Bazhenov, Ganchev and Vatev3, Reference Calvert, Cummins, Knight and Miller7, Reference Chisholm, Knight and Miller11, Reference Kalimullin19, Reference Kalimullin20]: What properties must classes of structures
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\mathcal {K}'$
have so that there is a Turing computable embedding from
$\mathcal {K}'$
have so that there is a Turing computable embedding from
![]() $\mathcal {K}$
to
$\mathcal {K}$
to
![]() $\mathcal {K}'$
but no computable embedding? Our pullback theorem is a useful tool for investigations of this kind. To demonstrate this we study classes
$\mathcal {K}'$
but no computable embedding? Our pullback theorem is a useful tool for investigations of this kind. To demonstrate this we study classes
![]() $\mathcal {K}$
and their sister classes
$\mathcal {K}$
and their sister classes
![]() $\tilde {\mathcal {K}}$
where
$\tilde {\mathcal {K}}$
where
![]() $\tilde {\mathcal {A}}$
is obtained from
$\tilde {\mathcal {A}}$
is obtained from
![]() $\mathcal {A}$
by introducing an infinite equivalence relation E on
$\mathcal {A}$
by introducing an infinite equivalence relation E on
![]() $\omega $
where all equivalence classes are infinite such that
$\omega $
where all equivalence classes are infinite such that
![]() $\tilde {\mathcal {A}}/E\cong \mathcal {A}$
. We continue work of Ganchev, Kalimullin, and Vatev [Reference Ganchev, Kalimullin and Vatev16] and study when we can have a computable embedding from
$\tilde {\mathcal {A}}/E\cong \mathcal {A}$
. We continue work of Ganchev, Kalimullin, and Vatev [Reference Ganchev, Kalimullin and Vatev16] and study when we can have a computable embedding from
![]() $\tilde {\mathcal {K}}$
into
$\tilde {\mathcal {K}}$
into
![]() $\mathcal {K}$
. We show that for
$\mathcal {K}$
. We show that for
![]() $\mathcal {L}$
the class of linear orderings, any two structures in
$\mathcal {L}$
the class of linear orderings, any two structures in
![]() $\tilde {\mathcal {L}}$
satisfy the same
$\tilde {\mathcal {L}}$
satisfy the same
![]() $\Sigma _2^p$
sentences. Thus, if
$\Sigma _2^p$
sentences. Thus, if
![]() $\mathcal {K}\subseteq \mathcal {L}$
, and the orderings in
$\mathcal {K}\subseteq \mathcal {L}$
, and the orderings in
![]() $\mathcal {K}$
are distinguishable by
$\mathcal {K}$
are distinguishable by
![]() $\Sigma ^p_2$
sentences, we cannot have a computable embedding
$\Sigma ^p_2$
sentences, we cannot have a computable embedding
![]() $\tilde {\mathcal {K}} \to \mathcal {K}$
. Using this we show that there is no embedding from
$\tilde {\mathcal {K}} \to \mathcal {K}$
. Using this we show that there is no embedding from
![]() $\{\tilde {\omega },\tilde {\omega }^{*}\}$
to
$\{\tilde {\omega },\tilde {\omega }^{*}\}$
to
![]() $\{\omega ,\omega ^{*}\}$
, answering a question of Kalimullin (Theorem 5.6).
$\{\omega ,\omega ^{*}\}$
, answering a question of Kalimullin (Theorem 5.6).
2 Preliminaries
2.1 Scott topology
Let
![]() $(P,\leq )$
be a partial order. A set
$(P,\leq )$
be a partial order. A set
![]() $D\subseteq P$
is directed if
$D\subseteq P$
is directed if
![]() $D\neq \emptyset $
and for all
$D\neq \emptyset $
and for all
![]() $a,b\in D$
, there is
$a,b\in D$
, there is
![]() $d\in D$
with
$d\in D$
with
![]() $a\leq d$
and
$a\leq d$
and
![]() $b\leq d$
. A partial order P is a directed complete partial order (dcpo) if every directed
$b\leq d$
. A partial order P is a directed complete partial order (dcpo) if every directed
![]() $D\subseteq P$
has a supremum
$D\subseteq P$
has a supremum
![]() $\sup D$
in P. A set U is Scott open if U is an upper set, i.e.,
$\sup D$
in P. A set U is Scott open if U is an upper set, i.e.,
![]() $x\in U$
and
$x\in U$
and
![]() $x\leq y\implies y\in U$
, and for every directed set D with
$x\leq y\implies y\in U$
, and for every directed set D with
![]() $\sup D\in U$
we have that
$\sup D\in U$
we have that
![]() $D\cap U\neq \emptyset $
. The Scott open sets of P form a topology on P, the Scott topology.
$D\cap U\neq \emptyset $
. The Scott open sets of P form a topology on P, the Scott topology.
Notice that the Scott topology on any partial ordered set that contains a chain of size larger than
![]() $2$
is not Hausdorff. To see this just note that for all
$2$
is not Hausdorff. To see this just note that for all
![]() $x,y\in P$
if
$x,y\in P$
if
![]() $x\leq y$
then every Scott open set containing x contains y. So, in particular, it is not Polish.
$x\leq y$
then every Scott open set containing x contains y. So, in particular, it is not Polish.
As an example of such a space consider the Scott topology on
![]() $2^\omega $
equipped with the dcpo given by
$2^\omega $
equipped with the dcpo given by
![]() $f\subseteq g$
if
$f\subseteq g$
if
![]() $f(i)=1 \implies g(i)=1$
. It has a natural countable basis given by the basic open sets
$f(i)=1 \implies g(i)=1$
. It has a natural countable basis given by the basic open sets
The Scott topology on
![]() $2^\omega $
is what is commonly referred to as an
$2^\omega $
is what is commonly referred to as an
![]() $\omega $
-continuous domain. In fact it is an
$\omega $
-continuous domain. In fact it is an
![]() $\omega $
-algebraic domain and thus a quasi-Polish space [Reference de Brecht6]. The spaces we consider in this paper will be closed subspaces of the Scott topology on
$\omega $
-algebraic domain and thus a quasi-Polish space [Reference de Brecht6]. The spaces we consider in this paper will be closed subspaces of the Scott topology on
![]() $2^\omega $
.
$2^\omega $
.
Let
![]() $\tau $
be a countable relational vocabulary containing
$\tau $
be a countable relational vocabulary containing
![]() $=$
and
$=$
and
![]() $\neq $
. Denote by
$\neq $
. Denote by
![]() $Mod(\tau )$
the set of countable
$Mod(\tau )$
the set of countable
![]() $\tau $
-structures with universe
$\tau $
-structures with universe
![]() $\omega $
. Similarly, if
$\omega $
. Similarly, if
![]() $\xi $
is a
$\xi $
is a
![]() $\tau $
-formula, denote by
$\tau $
-formula, denote by
![]() $Mod(\xi )$
the set of models of
$Mod(\xi )$
the set of models of
![]() $\xi $
. There is a natural dcpo on
$\xi $
. There is a natural dcpo on
![]() $Mod(\tau )$
given by
$Mod(\tau )$
given by
For the sake of readability we will refer to the Scott topology on
![]() $(Mod(\tau ),\preceq )$
simply as the Scott topology on
$(Mod(\tau ),\preceq )$
simply as the Scott topology on
![]() $Mod(\tau )$
. It might seem odd to the reader that we include both
$Mod(\tau )$
. It might seem odd to the reader that we include both
![]() $=$
and
$=$
and
![]() $\neq $
in the vocabulary. The reason for this is that we want to identify the Scott open subsets of
$\neq $
in the vocabulary. The reason for this is that we want to identify the Scott open subsets of
![]() $Mod(\tau )$
with subsets that are definable by existential formulas without negation. If
$Mod(\tau )$
with subsets that are definable by existential formulas without negation. If
![]() $\neq $
is not in the vocabulary, then this is generally not possible for the emptyset. With
$\neq $
is not in the vocabulary, then this is generally not possible for the emptyset. With
![]() $\neq $
in the vocabulary we can always define the emptyset by the formula
$\neq $
in the vocabulary we can always define the emptyset by the formula
![]() $\exists x\; x\neq x$
regardless of other properties of
$\exists x\; x\neq x$
regardless of other properties of
![]() $\tau $
.
$\tau $
.
In order to use tools from computability theory, it is convenient to represent
![]() $\mathcal {A}\in Mod(\tau )$
by their atomicFootnote
1
diagram—the infinite binary string
$\mathcal {A}\in Mod(\tau )$
by their atomicFootnote
1
diagram—the infinite binary string
 $$\begin{align*}D_{\mathcal{A}}(n)=\begin{cases} 1, & \text{if }\mathcal{A} \models \xi^{at}_n [x_i\to i], \\ 0, & \text{otherwise,}\end{cases}\end{align*}$$
$$\begin{align*}D_{\mathcal{A}}(n)=\begin{cases} 1, & \text{if }\mathcal{A} \models \xi^{at}_n [x_i\to i], \\ 0, & \text{otherwise,}\end{cases}\end{align*}$$
where
![]() $\xi ^{at}_n$
is the
$\xi ^{at}_n$
is the
![]() $n^{th}$
formula in an effective enumeration of all atomic
$n^{th}$
formula in an effective enumeration of all atomic
![]() $\tau $
-formulas with free variables a subset of
$\tau $
-formulas with free variables a subset of
![]() $\{x_0,\dots ,x_n\}$
. Notice that this representation gives a homeomorphism between
$\{x_0,\dots ,x_n\}$
. Notice that this representation gives a homeomorphism between
![]() $(Mod(\tau ),\preceq )$
and the closed subset of
$(Mod(\tau ),\preceq )$
and the closed subset of
![]() $(2^{\omega },\subseteq )$
given by
$(2^{\omega },\subseteq )$
given by
 $$\begin{align*}\bigcap_{n\in \{\ulcorner{x_i=x_j}\urcorner:i\neq j\in\omega\}} 2^\omega\setminus{O_{n}}\ \cap\ \bigcap_{n\in\{\ulcorner{x_i\neq x_i}\urcorner:i\in\omega\}} 2^\omega\setminus{O_n}.\end{align*}$$
$$\begin{align*}\bigcap_{n\in \{\ulcorner{x_i=x_j}\urcorner:i\neq j\in\omega\}} 2^\omega\setminus{O_{n}}\ \cap\ \bigcap_{n\in\{\ulcorner{x_i\neq x_i}\urcorner:i\in\omega\}} 2^\omega\setminus{O_n}.\end{align*}$$
Notice that the Scott topology on
![]() $Mod(\tau )$
is homeomorphic to the subspace topology on this space. By the same idea we can view natural classes of structures such as linear orderings as closed subspaces of
$Mod(\tau )$
is homeomorphic to the subspace topology on this space. By the same idea we can view natural classes of structures such as linear orderings as closed subspaces of
![]() $2^\omega $
.
$2^\omega $
.
2.2 The Borel hierarchy for non-metrizable spaces
The Borel sets of a Polish space bear a natural structure in terms of the Borel hierarchy. This is witnessed by the fact that the
![]() $\pmb\Sigma ^0_2$
sets are precisely the
$\pmb\Sigma ^0_2$
sets are precisely the
![]() $F_\sigma $
subsets and the
$F_\sigma $
subsets and the
![]() $\pmb\Pi ^0_2$
sets coincide with the
$\pmb\Pi ^0_2$
sets coincide with the
![]() $G_\delta $
subsets of the space. In non-Hausdorff spaces we cannot find this correspondence in general. It is common for non-Hausdorff spaces to have open sets that are not
$G_\delta $
subsets of the space. In non-Hausdorff spaces we cannot find this correspondence in general. It is common for non-Hausdorff spaces to have open sets that are not
![]() $F_\sigma $
(i.e., countable unions of closed sets) and closed sets that are not
$F_\sigma $
(i.e., countable unions of closed sets) and closed sets that are not
![]() $G_\delta $
(i.e., countable intersections of open sets). One example of this phenomenon is the Sierpiński space, which has
$G_\delta $
(i.e., countable intersections of open sets). One example of this phenomenon is the Sierpiński space, which has
![]() $\{\bot ,\top \}$
as underlying set and the singleton
$\{\bot ,\top \}$
as underlying set and the singleton
![]() $\{\top \}$
open but not closed. This implies that the classical definition of the Borel hierarchy, which defines level
$\{\top \}$
open but not closed. This implies that the classical definition of the Borel hierarchy, which defines level
![]() $\pmb\Sigma ^0_2$
as the
$\pmb\Sigma ^0_2$
as the
![]() $F_\sigma $
-sets and
$F_\sigma $
-sets and
![]() $\pmb\Pi ^0_2$
as the
$\pmb\Pi ^0_2$
as the
![]() $G_\delta $
-sets, is not appropriate in the general setting.
$G_\delta $
-sets, is not appropriate in the general setting.
Definition 2.1 [Reference Selivanov33].
Let
![]() $(X,\tau )$
be a topological space. For each countable ordinal
$(X,\tau )$
be a topological space. For each countable ordinal
![]() $\alpha \geq 1$
we define
$\alpha \geq 1$
we define
![]() $\pmb\Sigma ^0_\alpha (X,\tau )$
inductively as follows.
$\pmb\Sigma ^0_\alpha (X,\tau )$
inductively as follows.
-
(1)
 $\pmb\Sigma ^0_1(X,\tau ) = \tau $
.
$\pmb\Sigma ^0_1(X,\tau ) = \tau $
. -
(2) For
 $\alpha> 1$
,
$\alpha> 1$
,
 $\pmb\Sigma ^0_\alpha (X,\tau )$
is the set of all subsets A of X which can be expressed in the form where for each i,
$\pmb\Sigma ^0_\alpha (X,\tau )$
is the set of all subsets A of X which can be expressed in the form where for each i, $$\begin{align*}A = \bigcup_{i\in\omega}B_i \setminus B^{\prime}_i,\end{align*}$$
$$\begin{align*}A = \bigcup_{i\in\omega}B_i \setminus B^{\prime}_i,\end{align*}$$
 $B_i$
and
$B_i$
and
 $B^{\prime }_i$
are in
$B^{\prime }_i$
are in
 $\pmb\Sigma ^0_{\beta _i}(X,\tau )$
for some
$\pmb\Sigma ^0_{\beta _i}(X,\tau )$
for some
 $\beta _i < \alpha $
.
$\beta _i < \alpha $
.
We define
![]() $\pmb\Pi ^0_\alpha (X,\tau ) = \{X \setminus A \mid A \in \pmb\Sigma ^0_\alpha (X,\tau )\}$
and
$\pmb\Pi ^0_\alpha (X,\tau ) = \{X \setminus A \mid A \in \pmb\Sigma ^0_\alpha (X,\tau )\}$
and
![]() $\pmb\Delta ^0_\alpha (X,\tau ) = \pmb\Sigma ^0_\alpha (X,\tau ) \cap \pmb\Pi ^0_\alpha (X,\tau )$
. Finally, we define
$\pmb\Delta ^0_\alpha (X,\tau ) = \pmb\Sigma ^0_\alpha (X,\tau ) \cap \pmb\Pi ^0_\alpha (X,\tau )$
. Finally, we define
![]() $\mathbf {B}(X,\tau ) = \bigcup _{\alpha <\omega _1} \pmb\Sigma ^0_\alpha (X,\tau )$
to be the Borel subsets of
$\mathbf {B}(X,\tau ) = \bigcup _{\alpha <\omega _1} \pmb\Sigma ^0_\alpha (X,\tau )$
to be the Borel subsets of
![]() $(X,\tau )$
.
$(X,\tau )$
.
The definition above is equivalent to the classical definition of the Borel hierarchy on metrizable spaces, but differs in general. Selivanov has investigated this hierarchy in a series of papers [Reference Selivanov32, Reference Selivanov33], with an emphasis on applications to
![]() $\omega $
-continuous domains. He shows (Proposition 5.3 in [Reference Selivanov32]) that the classical Borel hierarchy on Cantor space differs from the new Borel hierarchy on the Scott space at finite levels and coincides at infinite levels.
$\omega $
-continuous domains. He shows (Proposition 5.3 in [Reference Selivanov32]) that the classical Borel hierarchy on Cantor space differs from the new Borel hierarchy on the Scott space at finite levels and coincides at infinite levels.
2.3 A hierarchy of positive infinitary formulas
In the classical setting the Lopez-Escobar theorem establishes a correspondence between subsets of
![]() $Mod(\tau )$
defined by sentences in the infinitary logic
$Mod(\tau )$
defined by sentences in the infinitary logic
![]() $L_{\omega _1\omega }$
and the Borel sets. Our theorem relates the Borel sets in the Scott topology with subsets defined by positive infinitary sentences defined below. See [Reference Ash and Knight1] for an in-depth treatment of infinitary logic that goes in hand with the developments in this section.
$L_{\omega _1\omega }$
and the Borel sets. Our theorem relates the Borel sets in the Scott topology with subsets defined by positive infinitary sentences defined below. See [Reference Ash and Knight1] for an in-depth treatment of infinitary logic that goes in hand with the developments in this section.
Definition 2.2. Fix a countable vocabulary
![]() $\tau $
. For every
$\tau $
. For every
![]() $\alpha <\omega _1$
define the sets of
$\alpha <\omega _1$
define the sets of
![]() $\Sigma ^p_\alpha $
and
$\Sigma ^p_\alpha $
and
![]() $\Pi ^p_\alpha $
$\Pi ^p_\alpha $
![]() $\tau $
-formulas inductively as follows.
$\tau $
-formulas inductively as follows.
-
• Let
 $\alpha = 0$
. Then:
$\alpha = 0$
. Then:-
– the
 $\Sigma ^p_0$
formulas are the finite conjunctions of atomic
$\Sigma ^p_0$
formulas are the finite conjunctions of atomic
 $\tau $
-formulas.
$\tau $
-formulas. -
– the
 $\Pi ^p_0$
formulas are the finite disjunctions of negations of atomic
$\Pi ^p_0$
formulas are the finite disjunctions of negations of atomic
 $\tau $
-formulas.
$\tau $
-formulas.
-
-
• Let
 $\alpha = 1$
. Then:
$\alpha = 1$
. Then:-
–
 $\varphi (\bar {u})$
is a
$\varphi (\bar {u})$
is a
 $\Sigma ^p_1$
formula if it has the form where for each
$\Sigma ^p_1$
formula if it has the form where for each
 $i \in I$
,
$i \in I$
,
 $\psi _i(\bar {u},\bar {x}_i)$
is a
$\psi _i(\bar {u},\bar {x}_i)$
is a
 $\Sigma ^p_0$
formula, I is countable.
$\Sigma ^p_0$
formula, I is countable.
-
–
 $\varphi (\bar {u})$
is a
$\varphi (\bar {u})$
is a
 $\Pi ^p_1$
formula if it has the form where for each
$\Pi ^p_1$
formula if it has the form where for each
 $i \in I$
,
$i \in I$
,
 $\psi _i(\bar {u},\bar {x}_i)$
is a
$\psi _i(\bar {u},\bar {x}_i)$
is a
 $\Pi ^p_0$
formula, I is countable.
$\Pi ^p_0$
formula, I is countable.
-
-
• Let
 $\alpha \geq 2$
. Then:
$\alpha \geq 2$
. Then:-
–
 $\varphi (\bar {u})$
is
$\varphi (\bar {u})$
is
 $\Sigma ^p_{\alpha }$
formula if it has the form where for each
$\Sigma ^p_{\alpha }$
formula if it has the form where for each
 $i \in I$
,
$i \in I$
,
 $\xi _i(\bar {u},\bar {x}_i)$
is a
$\xi _i(\bar {u},\bar {x}_i)$
is a
 $\Sigma ^p_{\beta _i}$
formula and
$\Sigma ^p_{\beta _i}$
formula and
 $\psi _i(\bar {u},\bar {x}_i)$
is a
$\psi _i(\bar {u},\bar {x}_i)$
is a
 $\Pi ^p_{\beta _i}$
formula, for some
$\Pi ^p_{\beta _i}$
formula, for some
 $\beta _i < \alpha $
and I countable.
$\beta _i < \alpha $
and I countable.
-
–
 $\varphi (\bar {u})$
is
$\varphi (\bar {u})$
is
 $\Pi ^p_{\alpha }$
formula if it has the form where for each
$\Pi ^p_{\alpha }$
formula if it has the form where for each
 $i \in I$
,
$i \in I$
,
 $\xi _i(\bar {u},\bar {x}_i)$
is a
$\xi _i(\bar {u},\bar {x}_i)$
is a
 $\Sigma ^p_{\beta _i}$
formula and
$\Sigma ^p_{\beta _i}$
formula and
 $\psi _i(\bar {u},\bar {x}_i)$
is a
$\psi _i(\bar {u},\bar {x}_i)$
is a
 $\Pi ^p_{\beta _i}$
formula, for some
$\Pi ^p_{\beta _i}$
formula, for some
 $\beta _i < \alpha $
and I countable.
$\beta _i < \alpha $
and I countable.
-
The set of positive infinitary formulas,
![]() $L^p_{\omega _1\omega }$
, is the smallest subset of
$L^p_{\omega _1\omega }$
, is the smallest subset of
![]() $L_{\omega _1\omega }$
closed under logical equivalence containing all
$L_{\omega _1\omega }$
closed under logical equivalence containing all
![]() $\Pi ^p_\alpha $
formulas for
$\Pi ^p_\alpha $
formulas for
![]() $\alpha <\omega _1$
.
$\alpha <\omega _1$
.
It is not hard to see that every
![]() $L_{\omega _1\omega }$
formula is logically equivalent to an
$L_{\omega _1\omega }$
formula is logically equivalent to an
![]() $L^p_{\omega _1\omega }$
-formula and that these two sets are thus equivalent. However, as should be evident from the definition, the hierarchies differ at finite levels.
$L^p_{\omega _1\omega }$
-formula and that these two sets are thus equivalent. However, as should be evident from the definition, the hierarchies differ at finite levels.
We say that a formula is in normal form if it is
![]() $\Sigma ^p_\alpha $
or
$\Sigma ^p_\alpha $
or
![]() $\Pi ^p_\alpha $
for some
$\Pi ^p_\alpha $
for some
![]() $\alpha <\omega _1$
. An easy transfinite induction shows that every
$\alpha <\omega _1$
. An easy transfinite induction shows that every
![]() $L_{\omega _1\omega }$
formula is equivalent to a formula in a normal form.
$L_{\omega _1\omega }$
formula is equivalent to a formula in a normal form.
Consider a
![]() $\Sigma ^p_1$
formula
$\Sigma ^p_1$
formula ![]() in a computable vocabulary
in a computable vocabulary
![]() $\tau $
. We can fix an injective computable enumeration of the conjunctions of atomic
$\tau $
. We can fix an injective computable enumeration of the conjunctions of atomic
![]() $\tau $
-formulas and assume without loss of generality that
$\tau $
-formulas and assume without loss of generality that
![]() $i=\ulcorner {\psi _i}\urcorner $
is the index of
$i=\ulcorner {\psi _i}\urcorner $
is the index of
![]() $\psi _i$
in this enumeration. Let
$\psi _i$
in this enumeration. Let
![]() $X\subseteq \omega $
such that I is X-c.e., then we say that
$X\subseteq \omega $
such that I is X-c.e., then we say that
![]() $\xi $
is an X-computable
$\xi $
is an X-computable
![]() $\Sigma ^p_1$
formula, or short,
$\Sigma ^p_1$
formula, or short,
![]() $\xi \in {\Sigma ^{p}_{1}{}^{,X}}$
. We will denote the set of
$\xi \in {\Sigma ^{p}_{1}{}^{,X}}$
. We will denote the set of
![]() $\Sigma ^p_1$
formulas such that I is c.e., as the
$\Sigma ^p_1$
formulas such that I is c.e., as the
![]() $\Sigma ^{pc}_1$
formulas, where c stands for computable.
$\Sigma ^{pc}_1$
formulas, where c stands for computable.
We could intuitively generalize the above definition to arbitrary X-computable
![]() $\alpha $
and X-computable
$\alpha $
and X-computable
![]() $\Pi ^p_\alpha $
formulas by demanding that all the index sets I are X-c.e. However, doing this formally requires some care. Let us give the formal definition for computable
$\Pi ^p_\alpha $
formulas by demanding that all the index sets I are X-c.e. However, doing this formally requires some care. Let us give the formal definition for computable
![]() $\Sigma ^p_\alpha $
and
$\Sigma ^p_\alpha $
and
![]() $\Pi ^p_\alpha $
. It should be obvious that this definition relativizes.
$\Pi ^p_\alpha $
. It should be obvious that this definition relativizes.
Definition 2.3. For
![]() $a \in \mathcal {O}$
, we define the index sets
$a \in \mathcal {O}$
, we define the index sets
![]() $S^\Sigma _a$
and
$S^\Sigma _a$
and
![]() $S^\Pi _a$
as follows:
$S^\Pi _a$
as follows:
-
• Let
 $|a|_{\mathcal {O}} = 0$
and
$|a|_{\mathcal {O}} = 0$
and
 $S^\Sigma _1 = \{\ulcorner {\varphi }\urcorner \mid \varphi \text { a finitary conjunction of atomic } \tau \text {-formulas}\}.$
$S^\Sigma _1 = \{\ulcorner {\varphi }\urcorner \mid \varphi \text { a finitary conjunction of atomic } \tau \text {-formulas}\}.$
-
• Let
 $|a|_{\mathcal {O}}> 0$
. Then:
$|a|_{\mathcal {O}}> 0$
. Then:-
–
 $S^\Sigma _{a} = \{\langle {\Sigma ,a,\overline {x},e}\rangle \mid \overline {x} \text { is a tuple of variables, } e \in \omega \}$
,
$S^\Sigma _{a} = \{\langle {\Sigma ,a,\overline {x},e}\rangle \mid \overline {x} \text { is a tuple of variables, } e \in \omega \}$
, -
–
 $S^\Pi _{a} = \{\langle {\Pi ,a,\overline {x},e}\rangle \mid \overline {x} \text { is a tuple of variables, } e \in \omega \}$
.
$S^\Pi _{a} = \{\langle {\Pi ,a,\overline {x},e}\rangle \mid \overline {x} \text { is a tuple of variables, } e \in \omega \}$
.
-
We define the positive infinitary formula
![]() $\varphi _i(\overline {u})$
with index i as follows.
$\varphi _i(\overline {u})$
with index i as follows.
-
• Let
 $|a|_{\mathcal {O}} = 0$
. If
$|a|_{\mathcal {O}} = 0$
. If
 $i \in S^\Sigma _1$
, then
$i \in S^\Sigma _1$
, then
 $\varphi _i(\overline {u})$
is the
$\varphi _i(\overline {u})$
is the
 $\tau $
-formula with Gödel number i.
$\tau $
-formula with Gödel number i. -
• Let
 $|a|_{\mathcal {O}} = 1$
. Then:
$|a|_{\mathcal {O}} = 1$
. Then:-
– If
 $i \in S^\Sigma _a$
, then
$i \in S^\Sigma _a$
, then
 $i = \langle {\Sigma ,a,\overline {u},e}\rangle $
, for some tuple
$i = \langle {\Sigma ,a,\overline {u},e}\rangle $
, for some tuple
 $\overline {u}$
and index e, and
$\overline {u}$
and index e, and
 $\varphi _i(\overline {u})$
is the disjunction of formulas
$\varphi _i(\overline {u})$
is the disjunction of formulas
 $(\exists \overline {x})\xi _j(\overline {u},\overline {x})$
, where
$(\exists \overline {x})\xi _j(\overline {u},\overline {x})$
, where
 $j \in W_e \cap S^\Sigma _1$
.
$j \in W_e \cap S^\Sigma _1$
. -
– If
 $i \in S^\Pi _a$
, then
$i \in S^\Pi _a$
, then
 $i = \langle {\Pi ,a,\overline {u},e}\rangle $
, for some tuple
$i = \langle {\Pi ,a,\overline {u},e}\rangle $
, for some tuple
 $\overline {u}$
and index e, and
$\overline {u}$
and index e, and
 $\varphi _i(\overline {u})$
is the conjunction of formulas
$\varphi _i(\overline {u})$
is the conjunction of formulas
 $(\forall \overline {x})\neg \xi _j(\overline {u},\overline {x})$
, where
$(\forall \overline {x})\neg \xi _j(\overline {u},\overline {x})$
, where
 $j \in W_e \cap S^\Sigma _1$
.
$j \in W_e \cap S^\Sigma _1$
.
-
-
• Let
 $|a|_{\mathcal {O}} \geq 2$
. Then:
$|a|_{\mathcal {O}} \geq 2$
. Then:-
– If
 $i \in S^\Sigma _a$
, then
$i \in S^\Sigma _a$
, then
 $i = \langle {\Sigma ,a,\overline {u},e}\rangle $
, for some tuple
$i = \langle {\Sigma ,a,\overline {u},e}\rangle $
, for some tuple
 $\overline {u}$
and index e, and
$\overline {u}$
and index e, and
 $\varphi _i(\overline {u})$
is the disjunction of formulas
$\varphi _i(\overline {u})$
is the disjunction of formulas
 $(\exists \overline {x})[\xi _\ell (\overline {u},\overline {x}) \land \psi _r(\overline {u},\overline {x})]$
, where
$(\exists \overline {x})[\xi _\ell (\overline {u},\overline {x}) \land \psi _r(\overline {u},\overline {x})]$
, where
 $\langle {\ell ,r}\rangle \in W_e$
and
$\langle {\ell ,r}\rangle \in W_e$
and
 $\ell \in S^\Sigma _b$
and
$\ell \in S^\Sigma _b$
and
 $r \in S^\Pi _b$
, for some
$r \in S^\Pi _b$
, for some
 $b <_{\mathcal {O}} a$
with
$b <_{\mathcal {O}} a$
with
 $|b|_{\mathcal {O}}> 0$
. Moreover, the third components of the indices
$|b|_{\mathcal {O}}> 0$
. Moreover, the third components of the indices
 $\ell $
and r are the tuple
$\ell $
and r are the tuple
 $(\overline {u},\overline {x})$
.
$(\overline {u},\overline {x})$
. -
– If
 $i \in S^\Pi _a$
, then
$i \in S^\Pi _a$
, then
 $i = \langle {\Pi ,a,\overline {u},e}\rangle $
, for some tuple
$i = \langle {\Pi ,a,\overline {u},e}\rangle $
, for some tuple
 $\overline {u}$
and index e, and
$\overline {u}$
and index e, and
 $\varphi _i(\overline {u})$
is the conjunction of formulas
$\varphi _i(\overline {u})$
is the conjunction of formulas
 $(\forall \overline {x})[\xi _\ell (\overline {u},\overline {x}) \lor \psi _r(\overline {u},\overline {x})]$
, where
$(\forall \overline {x})[\xi _\ell (\overline {u},\overline {x}) \lor \psi _r(\overline {u},\overline {x})]$
, where
 $\langle {\ell ,r}\rangle \in W_e$
and
$\langle {\ell ,r}\rangle \in W_e$
and
 $\ell \in S^\Sigma _b$
and
$\ell \in S^\Sigma _b$
and
 $r \in S^\Pi _b$
, for some
$r \in S^\Pi _b$
, for some
 $b <_{\mathcal {O}} a$
with
$b <_{\mathcal {O}} a$
with
 $|b|_{\mathcal {O}}> 0$
. Moreover, the third components of the indices
$|b|_{\mathcal {O}}> 0$
. Moreover, the third components of the indices
 $\ell $
and r are the tuple
$\ell $
and r are the tuple
 $(\overline {u},\overline {x})$
.
$(\overline {u},\overline {x})$
.
-
If
![]() $i\in S_a^\Sigma $
(
$i\in S_a^\Sigma $
(
![]() $S_a^\Pi $
) with
$S_a^\Pi $
) with
![]() $|a|=\alpha $
, then
$|a|=\alpha $
, then
![]() $\varphi _i\in \Sigma ^{pc}_\alpha $
(
$\varphi _i\in \Sigma ^{pc}_\alpha $
(
![]() $\Pi ^{pc}_\alpha $
). A formula
$\Pi ^{pc}_\alpha $
). A formula
![]() $\xi $
is a computable positive infinitary formula if
$\xi $
is a computable positive infinitary formula if
![]() $\xi \in L_{c\omega }^p=\bigcup _{\alpha <\omega _1^{\mathrm CK}} \Sigma _\alpha ^{pc}\cup \Pi _\alpha ^{pc}$
.
$\xi \in L_{c\omega }^p=\bigcup _{\alpha <\omega _1^{\mathrm CK}} \Sigma _\alpha ^{pc}\cup \Pi _\alpha ^{pc}$
.
Definition 2.3 can be relativized to arbitrary
![]() $X\subseteq \omega $
by replacing occurrences of
$X\subseteq \omega $
by replacing occurrences of
![]() $\mathcal O$
and
$\mathcal O$
and
![]() $W_e$
with
$W_e$
with
![]() $\mathcal O^X$
and
$\mathcal O^X$
and
![]() $W_e^X$
. This allows us to obtain
$W_e^X$
. This allows us to obtain
![]() ${\Sigma ^{p}_{\alpha }{}^{,X}}$
and
${\Sigma ^{p}_{\alpha }{}^{,X}}$
and
![]() ${\Pi ^{p}_{\alpha }{}^{,X}}$
formulas. As every
${\Pi ^{p}_{\alpha }{}^{,X}}$
formulas. As every
![]() $L^p_{\omega _1\omega }$
formula
$L^p_{\omega _1\omega }$
formula
![]() $\varphi $
is
$\varphi $
is
![]() $\Pi ^p_\alpha $
for some countable ordinal
$\Pi ^p_\alpha $
for some countable ordinal
![]() $\alpha $
,
$\alpha $
,
![]() $\varphi $
is
$\varphi $
is
![]() ${\Pi ^{p}_{\alpha }{}^{,X}}$
for X the computable join of the index sets in the definition of
${\Pi ^{p}_{\alpha }{}^{,X}}$
for X the computable join of the index sets in the definition of
![]() $\varphi $
and a set Y with
$\varphi $
and a set Y with
![]() $\alpha < \omega _1^Y$
. Hence, a formula is
$\alpha < \omega _1^Y$
. Hence, a formula is
![]() $\Pi ^p_\alpha $
if and only if it is
$\Pi ^p_\alpha $
if and only if it is
![]() ${\Pi ^{p}_{\alpha }{}^{,X}}$
for some
${\Pi ^{p}_{\alpha }{}^{,X}}$
for some
![]() $X\subseteq \omega $
.
$X\subseteq \omega $
.
Definition 2.4. We define
![]() $neg(\varphi )$
following the definition of
$neg(\varphi )$
following the definition of
![]() $\varphi $
.
$\varphi $
.
-
• Let
 $\alpha = 0$
.
$\alpha = 0$
.-
– If
 $\varphi $
is
$\varphi $
is
 $\Sigma ^p_0$
, i.e.,
$\Sigma ^p_0$
, i.e.,
 $\varphi $
is a conjunction over some finite set I of the atomic formulas
$\varphi $
is a conjunction over some finite set I of the atomic formulas
 $\varphi ^{at}_i$
, where
$\varphi ^{at}_i$
, where
 $i \in I$
, then
$i \in I$
, then
 $neg(\varphi )$
is the finite disjunction over the same finite set I of
$neg(\varphi )$
is the finite disjunction over the same finite set I of
 $\neg \varphi ^{at}_i$
, where
$\neg \varphi ^{at}_i$
, where
 $i \in I$
.
$i \in I$
. -
– If
 $\varphi $
is
$\varphi $
is
 $\Pi ^p_0$
, i.e.,
$\Pi ^p_0$
, i.e.,
 $\varphi $
is a disjunction over some finite set I of
$\varphi $
is a disjunction over some finite set I of
 $\neg \varphi ^{at}_i$
, where
$\neg \varphi ^{at}_i$
, where
 $i \in I$
, then
$i \in I$
, then
 $neg(\varphi )$
is the conjunction over the same finite set I of
$neg(\varphi )$
is the conjunction over the same finite set I of
 $\varphi ^{at}_i$
, where
$\varphi ^{at}_i$
, where
 $i \in I$
.
$i \in I$
.
-
-
• Let
 $\alpha = 1$
.
$\alpha = 1$
.-
– If
 $\varphi $
is
$\varphi $
is
 $\Sigma ^p_1$
, i.e.,
$\Sigma ^p_1$
, i.e.,
 $\varphi $
is an infinitary disjunction over a set of formulas of the form
$\varphi $
is an infinitary disjunction over a set of formulas of the form
 $\exists \bar {x} \psi $
, then
$\exists \bar {x} \psi $
, then
 $neg(\varphi )$
is an infinitary conjunction over the same set of the formulas
$neg(\varphi )$
is an infinitary conjunction over the same set of the formulas
 $\forall \bar {x} neg(\psi )$
.
$\forall \bar {x} neg(\psi )$
. -
– If
 $\varphi $
is
$\varphi $
is
 $\Pi ^p_1$
, i.e.,
$\Pi ^p_1$
, i.e.,
 $\varphi $
is an infinitary conjunction over a set of formulas of the form
$\varphi $
is an infinitary conjunction over a set of formulas of the form
 $\forall \bar {x} \psi $
, then
$\forall \bar {x} \psi $
, then
 $neg(\varphi )$
is an infinitary disjunction over the same set of the formulas
$neg(\varphi )$
is an infinitary disjunction over the same set of the formulas
 $\exists \bar {x} neg(\psi )$
.
$\exists \bar {x} neg(\psi )$
.
-
-
• Let
 $\alpha \geq 2$
.
$\alpha \geq 2$
.-
– If
 $\varphi $
is
$\varphi $
is
 $\Sigma ^p_{\alpha }$
formula, i.e.,
$\Sigma ^p_{\alpha }$
formula, i.e.,
 $\varphi $
is an infinitary disjunction over a set of formulas of the form
$\varphi $
is an infinitary disjunction over a set of formulas of the form
 $\exists \bar {x}(\xi \land \psi )$
, then
$\exists \bar {x}(\xi \land \psi )$
, then
 $neg(\varphi )$
is an infinitary conjunction over the same set of the formulas
$neg(\varphi )$
is an infinitary conjunction over the same set of the formulas
 $\forall \bar {x}(neg(\xi ) \lor neg(\psi ))$
.
$\forall \bar {x}(neg(\xi ) \lor neg(\psi ))$
. -
– If
 $\varphi $
is
$\varphi $
is
 $\Pi ^p_{\alpha }$
formula, i.e.,
$\Pi ^p_{\alpha }$
formula, i.e.,
 $\varphi $
is an infinitary conjunction over a set of formulas of the form
$\varphi $
is an infinitary conjunction over a set of formulas of the form
 $\forall \bar {x}(\xi \lor \psi )$
, then
$\forall \bar {x}(\xi \lor \psi )$
, then
 $neg(\varphi )$
is an infinitary disjunction over the same set of the formulas
$neg(\varphi )$
is an infinitary disjunction over the same set of the formulas
 $\exists \bar {x}(neg(\xi ) \land neg(\psi ))$
.
$\exists \bar {x}(neg(\xi ) \land neg(\psi ))$
.
-
If
![]() $\xi $
is not in normal form and thus not in
$\xi $
is not in normal form and thus not in
![]() $\Sigma ^p_\alpha $
or
$\Sigma ^p_\alpha $
or
![]() $\Pi ^p_\alpha $
for any
$\Pi ^p_\alpha $
for any
![]() $\alpha <\omega _1$
, then we can find a formula in normal form
$\alpha <\omega _1$
, then we can find a formula in normal form
![]() $\psi $
such that
$\psi $
such that
![]() $\psi \equiv \xi $
and let
$\psi \equiv \xi $
and let
![]() $neg(\xi )=neg(\psi )$
.
$neg(\xi )=neg(\psi )$
.
The above definition makes the proof of the following proposition self-evident.
Proposition 2.5. For any
![]() $L^p_{\omega _1\omega }$
formula
$L^p_{\omega _1\omega }$
formula
![]() $\varphi $
,
$\varphi $
,
![]() $neg(neg(\varphi )) \equiv \varphi $
. Furthermore, if
$neg(neg(\varphi )) \equiv \varphi $
. Furthermore, if
![]() $\varphi \in \Pi ^{pc}_\alpha $
, then
$\varphi \in \Pi ^{pc}_\alpha $
, then
![]() $neg(\varphi )\in \Sigma ^{pc}_\alpha $
and
$neg(\varphi )\in \Sigma ^{pc}_\alpha $
and
![]() $neg(neg(\varphi ))=\varphi $
.
$neg(neg(\varphi ))=\varphi $
.
Following [Reference Montalbán27, Chapter V.4], consider
![]() $L^p_{\omega _1\omega }$
formulas in the language of arithmetic with one extra unary relation symbol D, to represent the diagram of the structure, which we treat as a second-order variable. This means that we allow atomic formulas of the form
$L^p_{\omega _1\omega }$
formulas in the language of arithmetic with one extra unary relation symbol D, to represent the diagram of the structure, which we treat as a second-order variable. This means that we allow atomic formulas of the form
![]() $D(x)$
. We will refer to these formulas as
$D(x)$
. We will refer to these formulas as
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formulas. We can now talk about
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formulas. We can now talk about
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
definable subsets of
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
definable subsets of
![]() $2^{\omega }$
(or
$2^{\omega }$
(or
![]() $\text {Mod}(\tau )$
) in the standard model of arithmetic. A set of natural numbers A is
$\text {Mod}(\tau )$
) in the standard model of arithmetic. A set of natural numbers A is
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-definable if there is an
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-definable if there is an
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\xi $
such that
$\xi $
such that
![]() $(\mathbb {N},A)\models \xi $
where
$(\mathbb {N},A)\models \xi $
where
![]() $\mathbb {N}$
is the standard model of arithmetic. By identifying elements of
$\mathbb {N}$
is the standard model of arithmetic. By identifying elements of
![]() $2^{\omega }$
and
$2^{\omega }$
and
![]() $\text {Mod}(\tau )$
as characteristic functions of sets we get the notion of definability for these elements. Furthermore, it is not hard to see that within this model every
$\text {Mod}(\tau )$
as characteristic functions of sets we get the notion of definability for these elements. Furthermore, it is not hard to see that within this model every
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula is equivalent to an
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula is equivalent to an
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula without quantifiers, and that this quantifier elimination can be done without increasing the complexity of the formula. To see this, simply note that we can replace formulas of the form
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula without quantifiers, and that this quantifier elimination can be done without increasing the complexity of the formula. To see this, simply note that we can replace formulas of the form
![]() $\exists x \xi (x)$
by
$\exists x \xi (x)$
by ![]() and formulas of the form
and formulas of the form
![]() $\forall x \xi (x)$
by
$\forall x \xi (x)$
by ![]() where
where
![]() $\mathbf n$
is the formal term for n in
$\mathbf n$
is the formal term for n in
![]() $\mathbb {N}$
. Notice that the atomic subformulas of a quantifier-free
$\mathbb {N}$
. Notice that the atomic subformulas of a quantifier-free
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula are either
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula are either
![]() $D(\mathbf n)$
,
$D(\mathbf n)$
,
![]() $\top $
, or
$\top $
, or
![]() $\bot $
. We will refer to
$\bot $
. We will refer to
![]() $\Sigma ^p_\alpha $
formulas of this form as
$\Sigma ^p_\alpha $
formulas of this form as
![]() $\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formulas and to
$\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formulas and to
![]() $\Pi ^p_\alpha $
formulas as
$\Pi ^p_\alpha $
formulas as
![]() $\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formulas.
$\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formulas.
Proposition 2.6. For all non-zero
![]() $\alpha < \omega _1$
,
$\alpha < \omega _1$
,
-
(1)
 $\pmb\Sigma ^0_\alpha (2^\omega )=Mod(\mathbb {N}\mbox {-}\Sigma ^p_\alpha )=\left \{\{ X\in 2^\omega : (\mathbb N,X)\models \xi \}:\xi \in \mathbb {N}\mbox {-}\Sigma ^p_\alpha \right \},$
$\pmb\Sigma ^0_\alpha (2^\omega )=Mod(\mathbb {N}\mbox {-}\Sigma ^p_\alpha )=\left \{\{ X\in 2^\omega : (\mathbb N,X)\models \xi \}:\xi \in \mathbb {N}\mbox {-}\Sigma ^p_\alpha \right \},$
-
(2)
 $\pmb\Pi ^0_\alpha (2^\omega )=Mod(\mathbb {N}\mbox {-}\Pi ^p_\alpha )=\left \{\{ X\in 2^\omega : (\mathbb N,X)\models \xi \}:\xi \in \mathbb {N}\mbox {-}\Pi ^p_\alpha \right \}.$
$\pmb\Pi ^0_\alpha (2^\omega )=Mod(\mathbb {N}\mbox {-}\Pi ^p_\alpha )=\left \{\{ X\in 2^\omega : (\mathbb N,X)\models \xi \}:\xi \in \mathbb {N}\mbox {-}\Pi ^p_\alpha \right \}.$
Proof The proof is by induction on
![]() $\alpha $
. By our comments in the above paragraph we may assume that
$\alpha $
. By our comments in the above paragraph we may assume that
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formulas are quantifier-free and all atomic subformulas are of the form
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formulas are quantifier-free and all atomic subformulas are of the form
![]() $\top $
,
$\top $
,
![]() $\bot $
, or
$\bot $
, or
![]() $D(\mathbf n)$
for some
$D(\mathbf n)$
for some
![]() $n\in \omega $
. If
$n\in \omega $
. If
![]() $\xi \in \mathbb {N}\mbox {-}\Sigma ^p_{0}$
contains the subformula
$\xi \in \mathbb {N}\mbox {-}\Sigma ^p_{0}$
contains the subformula
![]() $\bot $
, then
$\bot $
, then
![]() $Mod(\xi )=\emptyset $
and if
$Mod(\xi )=\emptyset $
and if
![]() $\xi =\top $
, then
$\xi =\top $
, then
![]() $Mod(\xi )=2^\omega $
. Otherwise, the corresponding open set
$Mod(\xi )=2^\omega $
. Otherwise, the corresponding open set
![]() $X_\xi $
is
$X_\xi $
is
![]() $\bigcap _{n\in \omega : D(\mathbf n)\in sf(\xi )} O_n$
, where by
$\bigcap _{n\in \omega : D(\mathbf n)\in sf(\xi )} O_n$
, where by
![]() $sf(\xi )$
we denote the subformulas of
$sf(\xi )$
we denote the subformulas of
![]() $\xi $
.
$\xi $
.
If
![]() $\xi \in \mathbb {N}\mbox {-}\Sigma ^p_1$
, i.e.,
$\xi \in \mathbb {N}\mbox {-}\Sigma ^p_1$
, i.e., ![]() with
with
![]() $\psi _i\in \mathbb {N}\mbox {-}\Sigma _0^p$
, then
$\psi _i\in \mathbb {N}\mbox {-}\Sigma _0^p$
, then
![]() $Mod(\xi )=X_\xi =\bigcup _{i\in I} X_{\psi _i}\in \pmb\Sigma ^0_1$
. If
$Mod(\xi )=X_\xi =\bigcup _{i\in I} X_{\psi _i}\in \pmb\Sigma ^0_1$
. If
![]() $\xi \in \mathbb {N}\mbox {-}\Pi _1^p$
, then
$\xi \in \mathbb {N}\mbox {-}\Pi _1^p$
, then
![]() $\xi =neg(\psi )$
and
$\xi =neg(\psi )$
and
![]() $Mod(\xi )=Mod(neg(\psi ))=2^\omega \setminus {X_\psi }\in \pmb\Pi ^0_1$
. On the other hand, if
$Mod(\xi )=Mod(neg(\psi ))=2^\omega \setminus {X_\psi }\in \pmb\Pi ^0_1$
. On the other hand, if
![]() $B\in \pmb\Sigma ^0_1$
, i.e.,
$B\in \pmb\Sigma ^0_1$
, i.e.,
![]() $B=\bigcup _{i\in I}\bigcap _{n\leq N_i} O_{n}$
, then let
$B=\bigcup _{i\in I}\bigcap _{n\leq N_i} O_{n}$
, then let ![]() . If
. If
![]() $B\in \pmb\Pi ^0_1$
, then
$B\in \pmb\Pi ^0_1$
, then
![]() $2^\omega \setminus {B}\in \pmb\Sigma ^0_1$
,
$2^\omega \setminus {B}\in \pmb\Sigma ^0_1$
,
![]() $neg(\xi _{2^\omega \setminus {B}})\in \mathbb {N}\mbox {-}\Pi ^{p}_1$
and
$neg(\xi _{2^\omega \setminus {B}})\in \mathbb {N}\mbox {-}\Pi ^{p}_1$
and
![]() $B=Mod(neg(\xi _{2^\omega \setminus {B}}))$
.
$B=Mod(neg(\xi _{2^\omega \setminus {B}}))$
.
Assume that for all
![]() $\beta <\alpha $
and all
$\beta <\alpha $
and all
![]() $\mathbb {N}\mbox {-}\Sigma _\beta ^p$
formulas
$\mathbb {N}\mbox {-}\Sigma _\beta ^p$
formulas
![]() $\xi $
, there is a
$\xi $
, there is a
![]() $\pmb\Sigma ^0_\beta $
set
$\pmb\Sigma ^0_\beta $
set
![]() $X_\xi $
such that
$X_\xi $
such that
![]() $Mod(\xi )=X_\xi $
. Let
$Mod(\xi )=X_\xi $
. Let
![]() $\xi \in \mathbb {N}\mbox {-}\Sigma ^p_\alpha $
, i.e.,
$\xi \in \mathbb {N}\mbox {-}\Sigma ^p_\alpha $
, i.e., ![]() for
for
![]() $\psi _i,\theta _i\in \mathbb {N}\mbox {-}\Sigma ^p_{\beta _i}$
with
$\psi _i,\theta _i\in \mathbb {N}\mbox {-}\Sigma ^p_{\beta _i}$
with
![]() $\beta _i<\alpha $
. Then
$\beta _i<\alpha $
. Then
![]() $Mod(\xi )=\bigcup _{i\in I} X_{\psi _i}\setminus X_{\theta _i}=X_\xi \in \pmb\Sigma ^0_\alpha $
. If
$Mod(\xi )=\bigcup _{i\in I} X_{\psi _i}\setminus X_{\theta _i}=X_\xi \in \pmb\Sigma ^0_\alpha $
. If
![]() $\xi \in \mathbb {N}\mbox {-}\Pi ^p_\alpha $
, then
$\xi \in \mathbb {N}\mbox {-}\Pi ^p_\alpha $
, then
![]() $\xi =neg(\psi )$
for
$\xi =neg(\psi )$
for
![]() $\psi \in \Sigma ^p_\alpha $
and
$\psi \in \Sigma ^p_\alpha $
and
![]() $Mod(\xi )=Mod(neg(\psi ))=2^\omega \setminus {X_\psi }\in \pmb\Pi ^0_\alpha $
.
$Mod(\xi )=Mod(neg(\psi ))=2^\omega \setminus {X_\psi }\in \pmb\Pi ^0_\alpha $
.
Suppose that for all
![]() $\beta <\alpha $
and all
$\beta <\alpha $
and all
![]() $\pmb\Sigma ^0_\beta $
sets B, there is an
$\pmb\Sigma ^0_\beta $
sets B, there is an
![]() $\mathbb {N}\mbox {-}\Sigma ^{p}_\beta $
formula
$\mathbb {N}\mbox {-}\Sigma ^{p}_\beta $
formula
![]() $\xi _B$
such that
$\xi _B$
such that
![]() $Mod(\xi _B)=B$
. Assume that
$Mod(\xi _B)=B$
. Assume that
![]() $B\in \pmb\Sigma ^0_\alpha $
, i.e.,
$B\in \pmb\Sigma ^0_\alpha $
, i.e.,
![]() $B=\bigcup _{i\in I} B_i\setminus B_i'$
with
$B=\bigcup _{i\in I} B_i\setminus B_i'$
with
![]() $B_i,B_i'\in \pmb\Sigma ^0_{\beta _i}$
for
$B_i,B_i'\in \pmb\Sigma ^0_{\beta _i}$
for
![]() $\beta _i<\alpha $
. Then
$\beta _i<\alpha $
. Then ![]() and
and
![]() $Mod(\xi _B)=B$
. At last, let
$Mod(\xi _B)=B$
. At last, let
![]() $B\in \pmb\Pi ^0_\alpha $
, then
$B\in \pmb\Pi ^0_\alpha $
, then
![]() $2^\omega \setminus {B}\in \pmb\Sigma ^0_\alpha $
,
$2^\omega \setminus {B}\in \pmb\Sigma ^0_\alpha $
,
![]() $neg(\xi _{2^\omega \setminus {B}})\in \mathbb {N}\mbox {-}\Pi ^p_\alpha $
and
$neg(\xi _{2^\omega \setminus {B}})\in \mathbb {N}\mbox {-}\Pi ^p_\alpha $
and
![]() $Mod(neg(\xi _{2^\omega \setminus {B}}))=B$
.
$Mod(neg(\xi _{2^\omega \setminus {B}}))=B$
.
2.4 The effective Borel hierarchy
As we have discussed after Definition 2.3, every positive infinitary formula is computable relative to some oracle X. Proposition 2.6 associates to every Borel set a positive infinitary formula
![]() $\xi $
in the language of arithmetic with an additional unary relation symbol. This motivates the following definition of the effectively Borel hierarchy on
$\xi $
in the language of arithmetic with an additional unary relation symbol. This motivates the following definition of the effectively Borel hierarchy on
![]() $2^\omega $
and through this on
$2^\omega $
and through this on
![]() $Mod(\tau )$
for a given computable vocabulary
$Mod(\tau )$
for a given computable vocabulary
![]() $\tau $
.
$\tau $
.
Definition 2.7. Let
![]() $X\subseteq 2^\omega $
and
$X\subseteq 2^\omega $
and
![]() $Y\subseteq \omega $
.
$Y\subseteq \omega $
.
-
•
 $X\in \Sigma ^0_\alpha (Y)$
if there is a
$X\in \Sigma ^0_\alpha (Y)$
if there is a
 $\Sigma ^{p,Y}_\alpha $
$\Sigma ^{p,Y}_\alpha $
 $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-formula
 $\varphi $
such that
$\varphi $
such that
 $X=\{D:(\mathbb N,D)\models \varphi \}$
. A
$X=\{D:(\mathbb N,D)\models \varphi \}$
. A
 $\Sigma ^{p,Y}_\alpha $
index for
$\Sigma ^{p,Y}_\alpha $
index for
 $\varphi $
is a Y-computable index for X.
$\varphi $
is a Y-computable index for X. -
•
 $X\in \Pi ^0_\alpha (Y)$
if there is a
$X\in \Pi ^0_\alpha (Y)$
if there is a
 $\Pi ^{p,Y}_\alpha $
$\Pi ^{p,Y}_\alpha $
 $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-formula
 $\varphi $
such that
$\varphi $
such that
 $X=\{D:(\mathbb N,D)\models \varphi \}$
. A
$X=\{D:(\mathbb N,D)\models \varphi \}$
. A
 $\Pi ^{p,Y}_\alpha $
index for
$\Pi ^{p,Y}_\alpha $
index for
 $\varphi $
is a Y-computable index for X.
$\varphi $
is a Y-computable index for X.
Furthermore, X is effectively
![]() $\pmb\Sigma ^0_\alpha $
, or
$\pmb\Sigma ^0_\alpha $
, or
![]() $X\in \Sigma ^0_\alpha $
, if
$X\in \Sigma ^0_\alpha $
, if
![]() $X\in \Sigma ^0_\alpha (\emptyset )$
. Likewise, X is effectively
$X\in \Sigma ^0_\alpha (\emptyset )$
. Likewise, X is effectively
![]() $\pmb\Pi ^0_\alpha $
, or
$\pmb\Pi ^0_\alpha $
, or
![]() $X\in \Pi ^0_\alpha $
, if
$X\in \Pi ^0_\alpha $
, if
![]() $X\in \Pi ^0_\alpha (\emptyset )$
.
$X\in \Pi ^0_\alpha (\emptyset )$
.
3 The Lopez-Escobar theorem for positive infinitary formulas
The main goal of this section is to give a forcing proof of the Lopez-Escobar theorem and its related corollaries. The definition of our forcing relation is similar to the forcing relation in [Reference Soskov34], but our presentation of the forcing and the forcing poset are closer to [Reference Montalbán27].
Our forcing poset is the space of presentations of a fixed structure
![]() $\mathcal {A}$
. We produce a generic element
$\mathcal {A}$
. We produce a generic element
![]() $\mathcal G\cong \mathcal {A}$
that decides membership of the Borel sets on
$\mathcal G\cong \mathcal {A}$
that decides membership of the Borel sets on
![]() $\mathcal {A}$
. We represent the Borel sets by their
$\mathcal {A}$
. We represent the Borel sets by their
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formulas using the correspondence established in Proposition 2.6. Formally our forcing poset
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formulas using the correspondence established in Proposition 2.6. Formally our forcing poset
![]() $\mathcal P$
is the set of finite permutations of the natural numbers. We will build a generic enumeration g and let our generic proposition
$\mathcal P$
is the set of finite permutations of the natural numbers. We will build a generic enumeration g and let our generic proposition
![]() $\mathcal G=g^{-1}(\mathcal {A})$
. Let us start by defining our forcing relation.
$\mathcal G=g^{-1}(\mathcal {A})$
. Let us start by defining our forcing relation.
Definition 3.1 (Forcing relation).
Fix a countable structure
![]() $\mathcal {A}$
in a countable vocabulary and let
$\mathcal {A}$
in a countable vocabulary and let
![]() $\mathcal P$
be the set of all finite permutations of A, which by our assumption is
$\mathcal P$
be the set of all finite permutations of A, which by our assumption is
![]() $\omega $
. For a forcing condition
$\omega $
. For a forcing condition
![]() $p\in \mathcal P$
define the forcing relation
$p\in \mathcal P$
define the forcing relation
![]() $\Vdash _{\mathcal {A}}$
inductively for all
$\Vdash _{\mathcal {A}}$
inductively for all
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-formulas
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
-formulas
![]() $\varphi $
in normal form as follows.
$\varphi $
in normal form as follows.
-
(atom1)
 $p \Vdash _{\mathcal {A}} \top $
and
$p \Vdash _{\mathcal {A}} \top $
and
 $p \not \Vdash _{\mathcal {A}} \bot .$
$p \not \Vdash _{\mathcal {A}} \bot .$
-
(atom2)
 $p \Vdash _{\mathcal {A}} D(n)$
if
$p \Vdash _{\mathcal {A}} D(n)$
if
 $\mathcal {A} \models \xi ^{at}_n[x_i \mapsto p_i].$
$\mathcal {A} \models \xi ^{at}_n[x_i \mapsto p_i].$
-
(ℕ-Σ0 p ) If
 $\varphi =D(n_0) \land \cdots \land D(n_{k})$
, then
$\varphi =D(n_0) \land \cdots \land D(n_{k})$
, then
 $p \Vdash _{\mathcal {A}} \varphi $
if
$p \Vdash _{\mathcal {A}} \varphi $
if
 $p \Vdash _{\mathcal {A}} D(n_i)$
for all
$p \Vdash _{\mathcal {A}} D(n_i)$
for all
 $i \leq k$
.
$i \leq k$
. -
(ℕ-Σ1 p ) If
 , where
, where
 $\xi _i$
are
$\xi _i$
are
 $\mathbb {N}\mbox {-}\Sigma ^p_0$
formulas, then
$\mathbb {N}\mbox {-}\Sigma ^p_0$
formulas, then
 $p \Vdash _{\mathcal {A}} \varphi $
if for some
$p \Vdash _{\mathcal {A}} \varphi $
if for some
 $i \in I$
,
$i \in I$
,
 $p \Vdash _{\mathcal {A}} \xi _i$
.
$p \Vdash _{\mathcal {A}} \xi _i$
. -
(ℕ-Σ>1 p ) If
 , where for each
, where for each
 $i \in I$
,
$i \in I$
,
 $\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_{\beta _i}$
and
$\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_{\beta _i}$
and
 $\theta _i\in \mathbb {N}\mbox {-}\Pi ^p_{\beta _i}$
for some
$\theta _i\in \mathbb {N}\mbox {-}\Pi ^p_{\beta _i}$
for some
 $\beta _i>0$
, then
$\beta _i>0$
, then
 $p \Vdash _{\mathcal {A}} \varphi $
if
$p \Vdash _{\mathcal {A}} \varphi $
if
 $p \Vdash _{\mathcal {A}} \xi _i$
and
$p \Vdash _{\mathcal {A}} \xi _i$
and
 $p \Vdash _{\mathcal {A}} \theta _i$
for some
$p \Vdash _{\mathcal {A}} \theta _i$
for some
 $i \in I$
.
$i \in I$
. -
(ℕ-Π α p ) If
 $\varphi $
is an
$\varphi $
is an
 $\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula, for any
$\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula, for any
 $\alpha \geq 0$
, then
$\alpha \geq 0$
, then
 $p \Vdash _{\mathcal {A}} \varphi $
if for all
$p \Vdash _{\mathcal {A}} \varphi $
if for all
 $q \supseteq p$
,
$q \supseteq p$
,
 $q \not \Vdash _{\mathcal {A}} neg(\varphi )$
.
$q \not \Vdash _{\mathcal {A}} neg(\varphi )$
.
There is a subtle point to the definition of (atom2). If
![]() $\xi _n^{at}$
contains a variable symbol
$\xi _n^{at}$
contains a variable symbol
![]() $x_i$
with
$x_i$
with
![]() $i\geq |p|$
, then we regard
$i\geq |p|$
, then we regard
![]() $\xi _n^{at}[x_i\mapsto p_i]$
as false in
$\xi _n^{at}[x_i\mapsto p_i]$
as false in
![]() $\mathcal {A}$
and thus
$\mathcal {A}$
and thus
![]() $p\not \Vdash _{\mathcal {A}} D(n)$
in this case.
$p\not \Vdash _{\mathcal {A}} D(n)$
in this case.
Lemma 3.2 (Extension).
For any
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
and forcing condition p, if
$\varphi $
and forcing condition p, if
![]() $p \Vdash _{\mathcal {A}} \varphi $
and
$p \Vdash _{\mathcal {A}} \varphi $
and
![]() $p \subseteq q$
, then
$p \subseteq q$
, then
![]() $q \Vdash _{\mathcal {A}} \varphi $
.
$q \Vdash _{\mathcal {A}} \varphi $
.
Proof Straightforward induction on
![]() $\varphi $
.
$\varphi $
.
Lemma 3.3 (Consistency).
For any
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
and any forcing condition p, it is not the case that
$\varphi $
and any forcing condition p, it is not the case that
![]() $p \Vdash _{\mathcal {A}} \varphi $
and
$p \Vdash _{\mathcal {A}} \varphi $
and
![]() $p \Vdash _{\mathcal {A}} neg(\varphi )$
.
$p \Vdash _{\mathcal {A}} neg(\varphi )$
.
Proof Towards a contradiction, assume that for some
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
and some forcing condition p,
$\varphi $
and some forcing condition p,
![]() $p \Vdash _{\mathcal {A}} \varphi $
and
$p \Vdash _{\mathcal {A}} \varphi $
and
![]() $p \Vdash _{\mathcal {A}} neg(\varphi )$
. Without loss of generality, suppose that
$p \Vdash _{\mathcal {A}} neg(\varphi )$
. Without loss of generality, suppose that
![]() $\varphi $
is an
$\varphi $
is an
![]() $\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula, for some
$\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula, for some
![]() $\alpha $
. Then, clearly,
$\alpha $
. Then, clearly,
![]() $neg(\varphi )$
is an
$neg(\varphi )$
is an
![]() $\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula. It follows that, since
$\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula. It follows that, since
![]() $p \Vdash _{\mathcal {A}} neg(\varphi )$
, for all
$p \Vdash _{\mathcal {A}} neg(\varphi )$
, for all
![]() $q \supseteq p$
,
$q \supseteq p$
,
![]() $q \not \Vdash _{\mathcal {A}} neg(neg(\varphi ))$
and hence
$q \not \Vdash _{\mathcal {A}} neg(neg(\varphi ))$
and hence
![]() $p \not \Vdash _{\mathcal {A}} \varphi $
because
$p \not \Vdash _{\mathcal {A}} \varphi $
because
![]() $neg(neg(\varphi )) \equiv \varphi $
.
$neg(neg(\varphi )) \equiv \varphi $
.
Lemma 3.4 (Density).
For any
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
and forcing condition p, there is a forcing condition
$\varphi $
and forcing condition p, there is a forcing condition
![]() $q \supseteq p$
such that
$q \supseteq p$
such that
![]() $q \Vdash _{\mathcal {A}} \varphi $
or
$q \Vdash _{\mathcal {A}} \varphi $
or
![]() $q \Vdash _{\mathcal {A}} neg(\varphi )$
.
$q \Vdash _{\mathcal {A}} neg(\varphi )$
.
Proof Assume that there is an
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
and forcing condition p such that for all
$\varphi $
and forcing condition p such that for all
![]() $q \supseteq p$
,
$q \supseteq p$
,
![]() $q \not \Vdash _{\mathcal {A}} \varphi $
and
$q \not \Vdash _{\mathcal {A}} \varphi $
and
![]() $q \not \Vdash _{\mathcal {A}} neg(\varphi )$
. Without loss of generality, suppose that
$q \not \Vdash _{\mathcal {A}} neg(\varphi )$
. Without loss of generality, suppose that
![]() $\varphi $
is an
$\varphi $
is an
![]() $\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula. Hence,
$\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula. Hence,
![]() $neg(\varphi )$
is an
$neg(\varphi )$
is an
![]() $\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula. Since
$\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula. Since
![]() $p\not \Vdash _{\mathcal {A}} neg(\varphi )$
, it follows that for some
$p\not \Vdash _{\mathcal {A}} neg(\varphi )$
, it follows that for some
![]() $q \supseteq p$
,
$q \supseteq p$
,
![]() $q \Vdash _{\mathcal {A}} neg(neg(\varphi ))$
. But since
$q \Vdash _{\mathcal {A}} neg(neg(\varphi ))$
. But since
![]() $neg(neg(\varphi )) \equiv \varphi $
, we conclude that
$neg(neg(\varphi )) \equiv \varphi $
, we conclude that
![]() $q \Vdash _{\mathcal {A}} \varphi $
.
$q \Vdash _{\mathcal {A}} \varphi $
.
Definition 3.5. A bijection g is called a generic enumeration of
![]() $\mathcal {A}$
if for any
$\mathcal {A}$
if for any
![]() $\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formula
![]() $\varphi $
, there is
$\varphi $
, there is
![]() $p \subset g$
such that
$p \subset g$
such that
![]() $p \Vdash _{\mathcal {A}} \varphi $
or
$p \Vdash _{\mathcal {A}} \varphi $
or
![]() $p \Vdash _{\mathcal {A}} neg(\varphi )$
.
$p \Vdash _{\mathcal {A}} neg(\varphi )$
.
Lemma 3.6. Every
![]() $p\in \mathcal P$
can be extended to a generic enumeration g.
$p\in \mathcal P$
can be extended to a generic enumeration g.
Proof As the set of
![]() $\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formulas in normal form is countable, we can fix an enumeration
$\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formulas in normal form is countable, we can fix an enumeration
![]() $(\xi _n)_{n\in \omega }$
of these formulas and let
$(\xi _n)_{n\in \omega }$
of these formulas and let
![]() $F_n=\{ q\in \mathcal P: q\Vdash _{\mathcal {A}} \xi _n \lor q \Vdash _{\mathcal {A}} \neg (\xi _n)\}$
. By Lemma 3.4 every
$F_n=\{ q\in \mathcal P: q\Vdash _{\mathcal {A}} \xi _n \lor q \Vdash _{\mathcal {A}} \neg (\xi _n)\}$
. By Lemma 3.4 every
![]() $F_n$
is dense in
$F_n$
is dense in
![]() $\mathcal P$
. Define a sequence
$\mathcal P$
. Define a sequence
![]() $p=p_0\subseteq p_1\subseteq \cdots $
such that
$p=p_0\subseteq p_1\subseteq \cdots $
such that
![]() $p_{2n}\in F_n$
and
$p_{2n}\in F_n$
and
![]() $p_{2n+1}$
contains the least natural number not in
$p_{2n+1}$
contains the least natural number not in
![]() $p_{2n}$
. As all the
$p_{2n}$
. As all the
![]() $F_n$
are dense, this sequence is well-defined and
$F_n$
are dense, this sequence is well-defined and
![]() $g=\lim _{n\to \omega }p_n$
is generic.
$g=\lim _{n\to \omega }p_n$
is generic.
Theorem 3.7 (Forcing equals truth).
Let g be a generic enumeration of
![]() $\mathcal {A}$
and let
$\mathcal {A}$
and let
![]() $\mathcal {G} = g^{-1}(\mathcal {A})$
and
$\mathcal {G} = g^{-1}(\mathcal {A})$
and
![]() $D_{\mathcal {G}}$
be the atomic diagram of
$D_{\mathcal {G}}$
be the atomic diagram of
![]() $\mathcal {G}$
. Then for any
$\mathcal {G}$
. Then for any
![]() $\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formula
![]() $\varphi $
,
$\varphi $
,
Proof We prove this by transfinite induction on the
![]() $\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{c\omega }$
formula
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $\varphi $
be atomic. Then
$\varphi $
be atomic. Then
![]() $\varphi =\top $
,
$\varphi =\top $
,
![]() $\varphi =\bot $
or
$\varphi =\bot $
or
![]() $\varphi = D(\mathbf n)$
for some n. The first two cases follow trivially from the definition. For the third case, suppose that for some
$\varphi = D(\mathbf n)$
for some n. The first two cases follow trivially from the definition. For the third case, suppose that for some
![]() $p \subset g$
,
$p \subset g$
,
![]() $p \Vdash _{\mathcal {A}} D(\mathbf n)$
. Then
$p \Vdash _{\mathcal {A}} D(\mathbf n)$
. Then
![]() $p^{-1}(\mathcal {A}) \models \xi ^{at}_n[x_i \mapsto i]$
and, thus,
$p^{-1}(\mathcal {A}) \models \xi ^{at}_n[x_i \mapsto i]$
and, thus,
![]() $g^{-1}(\mathcal {A}) \models \xi ^{at}_n[x_i \mapsto i]$
, or, in other words,
$g^{-1}(\mathcal {A}) \models \xi ^{at}_n[x_i \mapsto i]$
, or, in other words,
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models D(\mathbf n)$
. For the converse, let
$(\mathbb {N}, D_{\mathcal {G}}) \models D(\mathbf n)$
. For the converse, let
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models D(\mathbf n)$
. By our convention that
$(\mathbb {N}, D_{\mathcal {G}}) \models D(\mathbf n)$
. By our convention that
![]() $\xi _n^{at}$
does not contain variable symbols
$\xi _n^{at}$
does not contain variable symbols
![]() $x_i$
for
$x_i$
for
![]() $i>n$
we have that for
$i>n$
we have that for
![]() $p = g\upharpoonright {n}$
,
$p = g\upharpoonright {n}$
,
![]() $p^{-1}(\mathcal {A}) \models \xi ^{at}_n[x_i \mapsto i]$
and hence
$p^{-1}(\mathcal {A}) \models \xi ^{at}_n[x_i \mapsto i]$
and hence
![]() $p \Vdash _{\mathcal {A}} D(n)$
. The equivalence for
$p \Vdash _{\mathcal {A}} D(n)$
. The equivalence for
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_0$
and
$\mathbb {N}\mbox {-}\Sigma ^{pc}_0$
and
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_1$
formulas follows easily.
$\mathbb {N}\mbox {-}\Sigma ^{pc}_1$
formulas follows easily.
Let
![]() $\varphi $
be equivalent to an
$\varphi $
be equivalent to an
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formula, for
$\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formula, for
![]() $\alpha \geq 2$
. Then
$\alpha \geq 2$
. Then ![]() , where for any
, where for any
![]() $i \in W_e$
,
$i \in W_e$
,
![]() $\xi _i$
is
$\xi _i$
is
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_{\beta _i}$
and
$\mathbb {N}\mbox {-}\Sigma ^{pc}_{\beta _i}$
and
![]() $\psi _i$
is
$\psi _i$
is
![]() $\mathbb {N}\mbox {-}\Pi ^{pc}_{\beta _i}$
for some
$\mathbb {N}\mbox {-}\Pi ^{pc}_{\beta _i}$
for some
![]() $\beta _i < \alpha $
. Suppose that for some
$\beta _i < \alpha $
. Suppose that for some
![]() $p \subset g$
,
$p \subset g$
,
![]() $p \Vdash _{\mathcal {A}} \varphi $
, i.e., for some
$p \Vdash _{\mathcal {A}} \varphi $
, i.e., for some
![]() $i \in W_e$
,
$i \in W_e$
,
![]() $p \Vdash _{\mathcal {A}} \xi _i$
and
$p \Vdash _{\mathcal {A}} \xi _i$
and
![]() $p \Vdash _{\mathcal {A}} \psi _i$
. By the induction hypothesis,
$p \Vdash _{\mathcal {A}} \psi _i$
. By the induction hypothesis,
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models \xi _i$
and
$(\mathbb {N}, D_{\mathcal {G}}) \models \xi _i$
and
![]() $(\mathbb {N}, D_{\mathcal {G}})\models \psi _i$
and hence
$(\mathbb {N}, D_{\mathcal {G}})\models \psi _i$
and hence
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models \varphi $
. For the converse, let
$(\mathbb {N}, D_{\mathcal {G}}) \models \varphi $
. For the converse, let
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models \varphi $
. Then
$(\mathbb {N}, D_{\mathcal {G}}) \models \varphi $
. Then
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models \xi _i$
and
$(\mathbb {N}, D_{\mathcal {G}}) \models \xi _i$
and
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models \psi _i$
for some
$(\mathbb {N}, D_{\mathcal {G}}) \models \psi _i$
for some
![]() $i \in W_e$
. By the induction hypothesis, there is some
$i \in W_e$
. By the induction hypothesis, there is some
![]() $p_0 \subset g$
such that
$p_0 \subset g$
such that
![]() $p_0 \Vdash _{\mathcal {A}} \xi _i$
and some
$p_0 \Vdash _{\mathcal {A}} \xi _i$
and some
![]() $p_1 \subset g$
such that
$p_1 \subset g$
such that
![]() $p_1 \Vdash _{\mathcal {A}} \psi _i$
. Let
$p_1 \Vdash _{\mathcal {A}} \psi _i$
. Let
![]() $p = \max \{p_0, p_1\}$
. Clearly,
$p = \max \{p_0, p_1\}$
. Clearly,
![]() $p \subset g$
. By monotonicity of forcing,
$p \subset g$
. By monotonicity of forcing,
![]() $p \Vdash _{\mathcal {A}} \xi _i$
and
$p \Vdash _{\mathcal {A}} \xi _i$
and
![]() $p \Vdash _{\mathcal {A}} \psi _i$
. It follows that
$p \Vdash _{\mathcal {A}} \psi _i$
. It follows that
![]() $p \Vdash _{\mathcal {A}} \varphi $
.
$p \Vdash _{\mathcal {A}} \varphi $
.
Now let us consider the case when
![]() $\varphi $
is equivalent to an
$\varphi $
is equivalent to an
![]() $\mathbb {N}\mbox {-}\Pi ^{pc}_\alpha $
formula, for any
$\mathbb {N}\mbox {-}\Pi ^{pc}_\alpha $
formula, for any
![]() $\alpha \geq 0$
. First, let
$\alpha \geq 0$
. First, let
![]() $p \Vdash _{\mathcal {A}} \varphi $
for some
$p \Vdash _{\mathcal {A}} \varphi $
for some
![]() $p \subset g$
. Towards a contradiction, assume that
$p \subset g$
. Towards a contradiction, assume that
![]() $(\mathbb {N}, D_{\mathcal {G}}) \not \models \varphi $
. But then
$(\mathbb {N}, D_{\mathcal {G}}) \not \models \varphi $
. But then
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models neg(\varphi )$
, where
$(\mathbb {N}, D_{\mathcal {G}}) \models neg(\varphi )$
, where
![]() $neg(\varphi )$
is
$neg(\varphi )$
is
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
. It follows that for some
$\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
. It follows that for some
![]() $q \subset g$
,
$q \subset g$
,
![]() $q \Vdash _{\mathcal {A}} neg(\varphi )$
. Let
$q \Vdash _{\mathcal {A}} neg(\varphi )$
. Let
![]() $r = \max \{p ,q\}$
. By monotonicity, it follows that
$r = \max \{p ,q\}$
. By monotonicity, it follows that
![]() $r \Vdash _{\mathcal {A}} \varphi $
and
$r \Vdash _{\mathcal {A}} \varphi $
and
![]() $r \Vdash _{\mathcal {A}} neg(\varphi )$
. A contradiction.
$r \Vdash _{\mathcal {A}} neg(\varphi )$
. A contradiction.
Second, let
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models \varphi $
. Assume that for all
$(\mathbb {N}, D_{\mathcal {G}}) \models \varphi $
. Assume that for all
![]() $p \subset g$
,
$p \subset g$
,
![]() $p \not \Vdash _{\mathcal {A}} \varphi $
. But then, since g is generic, there is some
$p \not \Vdash _{\mathcal {A}} \varphi $
. But then, since g is generic, there is some
![]() $q \subset g$
such that
$q \subset g$
such that
![]() $q \Vdash _{\mathcal {A}} neg(\varphi )$
. Since
$q \Vdash _{\mathcal {A}} neg(\varphi )$
. Since
![]() $neg(\varphi )$
is
$neg(\varphi )$
is
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
, it follows that
$\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
, it follows that
![]() $(\mathbb {N}, D_{\mathcal {G}}) \models neg(\varphi )$
. We reach a contradiction.
$(\mathbb {N}, D_{\mathcal {G}}) \models neg(\varphi )$
. We reach a contradiction.
3.1 Definability of forcing
For any
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
, we will define an
$\varphi $
, we will define an
![]() $L^p_{\omega _1\omega }$
formula
$L^p_{\omega _1\omega }$
formula
![]() ${Force}_\varphi (\bar {u})$
such that
${Force}_\varphi (\bar {u})$
such that
Definition 3.8. For any
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
in normal form and every tuple
$\varphi $
in normal form and every tuple
![]() $\bar u\in \omega ^{<\omega }$
, define the formula
$\bar u\in \omega ^{<\omega }$
, define the formula
![]() ${Force}_\varphi (\bar u)$
inductively as follows.
${Force}_\varphi (\bar u)$
inductively as follows.
-
(atom1)
 ${Force}_\top (\bar u)=\exists x\; x=x$
and
${Force}_\top (\bar u)=\exists x\; x=x$
and
 ${Force}_\bot (\bar u)=\exists x\exists y (x\neq y\land x=y)$
.
${Force}_\bot (\bar u)=\exists x\exists y (x\neq y\land x=y)$
. -
(atom2) If
 $\varphi =D(n)$
, then
$\varphi =D(n)$
, then
 ${Force}_{\varphi }(\bar {u}) = \bigwedge _{i\neq j\ \&\ i,j<n}u_i \neq u_j\ \&\ \xi ^{at}_n[x_i \mapsto u_i]$
.
${Force}_{\varphi }(\bar {u}) = \bigwedge _{i\neq j\ \&\ i,j<n}u_i \neq u_j\ \&\ \xi ^{at}_n[x_i \mapsto u_i]$
. -
(ℕ-Σ0 p ) If
 with
with
 $\xi _i$
atomic, then
$\xi _i$
atomic, then  .
. -
(ℕ-Σ1 p ) If
 where
where
 $\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_0$
, then
$\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_0$
, then  .
. -
(ℕ-Σ>1 p ) If
 where
where
 $\xi _i\in \mathbb {N}\mbox {-}\Sigma _{\beta _i}^p$
and
$\xi _i\in \mathbb {N}\mbox {-}\Sigma _{\beta _i}^p$
and
 $\theta _i\in \mathbb {N}\mbox {-}\Pi ^p_{\beta _i}$
,
$\theta _i\in \mathbb {N}\mbox {-}\Pi ^p_{\beta _i}$
,
 $\beta _i>0$
, then
$\beta _i>0$
, then 
-
(ℕ-Π α p )
 .
.
Notice that the definition of
![]() ${Force}_\varphi (\bar u)$
only depends on the formula
${Force}_\varphi (\bar u)$
only depends on the formula
![]() $\varphi $
and the size of the tuple
$\varphi $
and the size of the tuple
![]() $\bar u$
. It depends neither on the tuple
$\bar u$
. It depends neither on the tuple
![]() $\bar u$
itself nor on the structure
$\bar u$
itself nor on the structure
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Lemma 3.9. For all
![]() $\alpha \geq 1$
, for each
$\alpha \geq 1$
, for each
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formula
$\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formula
![]() $\varphi $
,
$\varphi $
,
![]() ${Force}_\varphi $
is a
${Force}_\varphi $
is a
![]() $\Sigma ^{pc}_\alpha $
$\Sigma ^{pc}_\alpha $
![]() $\tau $
-formula.
$\tau $
-formula.
Proof This is proven by transfinite induction on
![]() $\alpha $
.
$\alpha $
.
-
• Let
 $\varphi $
be an
$\varphi $
be an
 $\mathbb {N}\mbox {-}\Sigma ^p_0$
formula. Since
$\mathbb {N}\mbox {-}\Sigma ^p_0$
formula. Since
 $\neq $
is included in
$\neq $
is included in
 $\tau $
, the formula
$\tau $
, the formula
 ${Force}_\varphi $
is a finite conjunction of finite
${Force}_\varphi $
is a finite conjunction of finite
 $\Sigma ^p_1$
formulas and hence it is a
$\Sigma ^p_1$
formulas and hence it is a
 $\Sigma ^{p}_1$
formula.
$\Sigma ^{p}_1$
formula. -
• Let
 $\varphi $
be an
$\varphi $
be an
 $\mathbb {N}\mbox {-}\Sigma ^p_1$
formula. Then
$\mathbb {N}\mbox {-}\Sigma ^p_1$
formula. Then  , where all
, where all
 $\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_0$
. We know that
$\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_0$
. We know that
 ${Force}_{\xi _i}(\overline {u})$
is
${Force}_{\xi _i}(\overline {u})$
is
 $\Sigma ^p_0$
for any tuple
$\Sigma ^p_0$
for any tuple
 $\overline {u}$
. Then is a
$\overline {u}$
. Then is a
 $\Sigma ^p_1$
$\Sigma ^p_1$
 $\tau $
-formula.
$\tau $
-formula.
-
• Let
 $\varphi $
be an
$\varphi $
be an
 $\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula,
$\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula,
 $\alpha \geq 2$
. Then
$\alpha \geq 2$
. Then  , where
, where
 $\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_\beta $
and
$\xi _i\in \mathbb {N}\mbox {-}\Sigma ^p_\beta $
and
 $\theta _i\in \mathbb {N}\mbox {-}\Pi ^p_\beta $
, for some
$\theta _i\in \mathbb {N}\mbox {-}\Pi ^p_\beta $
, for some
 $\beta < \alpha $
. Without loss of generality, we may suppose that
$\beta < \alpha $
. Without loss of generality, we may suppose that
 $\beta \geq 1$
. By the induction hypothesis, we know that
$\beta \geq 1$
. By the induction hypothesis, we know that
 ${Force}_{\xi _i}(\overline {u})$
is
${Force}_{\xi _i}(\overline {u})$
is
 $\Sigma ^p_\beta $
and
$\Sigma ^p_\beta $
and
 ${Force}_{\theta _i}(\overline {u})$
is
${Force}_{\theta _i}(\overline {u})$
is
 $\Pi ^p_\beta $
. is a computable infinitary
$\Pi ^p_\beta $
. is a computable infinitary
 $\Sigma ^p_\alpha $
$\Sigma ^p_\alpha $
 $\tau $
-formula.
$\tau $
-formula.
-
• Let
 $\varphi $
be an
$\varphi $
be an
 $\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula, for any
$\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula, for any
 $\alpha \geq 0$
. Then clearly,
$\alpha \geq 0$
. Then clearly,
 $neg(\varphi )$
is an
$neg(\varphi )$
is an
 $\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula. It follows that
$\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
formula. It follows that
 ${Force}_{neg(\varphi )}(\overline {u})$
is a
${Force}_{neg(\varphi )}(\overline {u})$
is a
 $\Sigma ^p_\alpha $
$\Sigma ^p_\alpha $
 $\tau $
-formula for any tuple
$\tau $
-formula for any tuple
 $\overline {u}$
. Then
$\overline {u}$
. Then
 $neg({Force}_{neg(\xi _i)}(\overline {u}))$
is
$neg({Force}_{neg(\xi _i)}(\overline {u}))$
is
 $\Pi ^p_\alpha $
and hence is
$\Pi ^p_\alpha $
and hence is
 $\Pi ^p_\alpha $
formula if
$\Pi ^p_\alpha $
formula if
 $\alpha \geq 1$
and
$\alpha \geq 1$
and
 $\Pi ^p_1$
if
$\Pi ^p_1$
if
 $\alpha = 0$
.
$\alpha = 0$
.
We still have to establish that if
![]() $\varphi $
is computable
$\varphi $
is computable
![]() $\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
, then
$\mathbb {N}\mbox {-}\Sigma ^p_\alpha $
, then
![]() ${Force}_{\varphi }(\bar u)$
is computable
${Force}_{\varphi }(\bar u)$
is computable
![]() $\Sigma ^p_\alpha $
. Just notice that given an index set for an
$\Sigma ^p_\alpha $
. Just notice that given an index set for an
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formula
$\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formula
![]() $\varphi $
our inductive definition of
$\varphi $
our inductive definition of
![]() ${Force}_{\varphi }(\bar u)$
describes an algorithm that produces an index set for a
${Force}_{\varphi }(\bar u)$
describes an algorithm that produces an index set for a
![]() $\Sigma ^{pc}_\alpha $
formula equivalent to
$\Sigma ^{pc}_\alpha $
formula equivalent to
![]() ${Force}_{\varphi }(\bar u)$
.
${Force}_{\varphi }(\bar u)$
.
Lemma 3.10 (Definability of forcing).
For any forcing condition p and any
![]() $\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
$\mathbb {N}\mbox {-}L^{p}_{\omega _1\omega }$
formula
![]() $\varphi $
,
$\varphi $
,
![]() $p \Vdash _{\mathcal {A}} \varphi $
iff
$p \Vdash _{\mathcal {A}} \varphi $
iff
![]() $\mathcal {A} \models {Force}_{\varphi }(\bar {p})$
.
$\mathcal {A} \models {Force}_{\varphi }(\bar {p})$
.
Proof Induction on
![]() $\varphi $
.
$\varphi $
.
For classes of structures
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
![]() $\mathcal {D}$
, and
$\mathcal {D}$
, and
![]() $\mathcal {K}$
, we say that
$\mathcal {K}$
, we say that
![]() $\mathcal {C} = \mathcal {D}$
within
$\mathcal {C} = \mathcal {D}$
within
![]() $\mathcal {K}$
if
$\mathcal {K}$
if
![]() $\mathcal {C} \cap \mathcal {K} = \mathcal {D} \cap \mathcal {K}$
. We essentially repeat the proof in [Reference Montalbán27] to obtain an effective version of Lopez-Escobar’s theorem.
$\mathcal {C} \cap \mathcal {K} = \mathcal {D} \cap \mathcal {K}$
. We essentially repeat the proof in [Reference Montalbán27] to obtain an effective version of Lopez-Escobar’s theorem.
Theorem 3.11. Let
![]() $\mathcal {K} \subseteq \text {Mod}(\tau )$
be isomorphism invariant. Suppose that for
$\mathcal {K} \subseteq \text {Mod}(\tau )$
be isomorphism invariant. Suppose that for
![]() $\alpha \geq 1$
, i is an index for a
$\alpha \geq 1$
, i is an index for a
![]() $\Pi ^0_\alpha $
set
$\Pi ^0_\alpha $
set
![]() $B_i$
in the effective Borel hierarchy such that
$B_i$
in the effective Borel hierarchy such that
![]() $B_i \cap \mathcal {K}$
is isomorphism invariant. Then we can effectively find an index for a
$B_i \cap \mathcal {K}$
is isomorphism invariant. Then we can effectively find an index for a
![]() $\Pi ^{pc}_\alpha $
$\Pi ^{pc}_\alpha $
![]() $\tau $
-sentence
$\tau $
-sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $B_i = \text{Mod}(\varphi)$
within
$B_i = \text{Mod}(\varphi)$
within
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Proof Consider a
![]() $\Pi ^0_\alpha $
set
$\Pi ^0_\alpha $
set
![]() $B_i$
in the effective Borel hierarchy. We can effectively find an index j of an
$B_i$
in the effective Borel hierarchy. We can effectively find an index j of an
![]() $\mathbb {N}\mbox {-}\Pi ^{pc}_\alpha $
formula
$\mathbb {N}\mbox {-}\Pi ^{pc}_\alpha $
formula
![]() $\xi $
such that
$\xi $
such that
![]() $B_i = \text {Mod}(\xi )$
. By Lemmas 3.9 and 3.10 we can effectively find an index for the
$B_i = \text {Mod}(\xi )$
. By Lemmas 3.9 and 3.10 we can effectively find an index for the
![]() $\Pi ^{pc}_\alpha $
$\Pi ^{pc}_\alpha $
![]() $\tau $
-sentence
$\tau $
-sentence
![]() $\varphi ={Force}_{\xi }(\langle {}\rangle )$
where
$\varphi ={Force}_{\xi }(\langle {}\rangle )$
where
![]() $\langle {}\rangle $
denotes the empty forcing condition. We will show that
$\langle {}\rangle $
denotes the empty forcing condition. We will show that
![]() $B_i = \text {Mod}(\varphi )$
within
$B_i = \text {Mod}(\varphi )$
within
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
First, let
![]() $\mathcal {A} \in B_i \cap \mathcal {K}$
. We must show that
$\mathcal {A} \in B_i \cap \mathcal {K}$
. We must show that
![]() $\mathcal {A} \models \varphi $
. Towards a contradiction, assume
$\mathcal {A} \models \varphi $
. Towards a contradiction, assume
![]() $\mathcal {A} \not \models \varphi $
. Then, by Lemma 3.10,
$\mathcal {A} \not \models \varphi $
. Then, by Lemma 3.10,
![]() $\langle {}\rangle \not \Vdash _{\mathcal {A}} \xi $
. Since
$\langle {}\rangle \not \Vdash _{\mathcal {A}} \xi $
. Since
![]() $\xi $
is
$\xi $
is
![]() $\mathbb {N}\mbox {-}\Pi ^p_\alpha $
, by Definition 3.1, there is a forcing condition q such that
$\mathbb {N}\mbox {-}\Pi ^p_\alpha $
, by Definition 3.1, there is a forcing condition q such that
![]() $q \Vdash _{\mathcal {A}} neg(\xi )$
. Extend q to a generic enumeration g of
$q \Vdash _{\mathcal {A}} neg(\xi )$
. Extend q to a generic enumeration g of
![]() $\mathcal {A}$
and consider
$\mathcal {A}$
and consider
![]() $\mathcal {G} = g^{-1}(\mathcal {A})$
. But then by Theorem 3.7,
$\mathcal {G} = g^{-1}(\mathcal {A})$
. But then by Theorem 3.7,
![]() $(\mathbb {N}, D_{\mathcal {G}})\models neg(\xi )$
. As
$(\mathbb {N}, D_{\mathcal {G}})\models neg(\xi )$
. As
![]() $\text {Mod}(neg(\xi ))=2^\omega \setminus {B_i}$
,
$\text {Mod}(neg(\xi ))=2^\omega \setminus {B_i}$
,
![]() $\mathcal {G}\in 2^\omega \setminus {B_i}$
. But
$\mathcal {G}\in 2^\omega \setminus {B_i}$
. But
![]() $B_i\ni \mathcal {A}$
was invariant and thus, as
$B_i\ni \mathcal {A}$
was invariant and thus, as
![]() $\mathcal {A}\cong \mathcal {G}$
,
$\mathcal {A}\cong \mathcal {G}$
,
![]() $\mathcal {G}\in B_i$
, a contradiction.
$\mathcal {G}\in B_i$
, a contradiction.
Second, let
![]() $\mathcal {A} \in \text {Mod}(\varphi ) \cap \mathcal {K}$
. Then
$\mathcal {A} \in \text {Mod}(\varphi ) \cap \mathcal {K}$
. Then
![]() $\mathcal {A} \models \varphi $
and hence
$\mathcal {A} \models \varphi $
and hence
![]() $\langle {}\rangle \Vdash _{\mathcal {A}} \xi $
. Consider any generic copy
$\langle {}\rangle \Vdash _{\mathcal {A}} \xi $
. Consider any generic copy
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() $\mathcal {A}$
. By Theorem 3.7,
$\mathcal {A}$
. By Theorem 3.7,
![]() $(\mathbb {N},D_{\mathcal {G}}) \models \xi $
and hence
$(\mathbb {N},D_{\mathcal {G}}) \models \xi $
and hence
![]() $\mathcal {G} \in \text {Mod}(\xi ) \cap \mathcal {K}$
. Since
$\mathcal {G} \in \text {Mod}(\xi ) \cap \mathcal {K}$
. Since
![]() $\text {Mod}(\xi ) \cap \mathcal {K}$
is closed under isomorphism,
$\text {Mod}(\xi ) \cap \mathcal {K}$
is closed under isomorphism,
![]() $\mathcal {A} \in \text {Mod}(\xi ) \cap \mathcal {K}=B_i\cap \mathcal {K}$
.
$\mathcal {A} \in \text {Mod}(\xi ) \cap \mathcal {K}=B_i\cap \mathcal {K}$
.
Notice that Theorem 3.11 also works for
![]() $\Sigma ^{pc}_\alpha $
sets as
$\Sigma ^{pc}_\alpha $
sets as
![]() $neg$
is a computable function that takes an index for a
$neg$
is a computable function that takes an index for a
![]() $\Sigma ^{pc}_\alpha $
set and outputs an index for a
$\Sigma ^{pc}_\alpha $
set and outputs an index for a
![]() $\Pi ^{pc}_\alpha $
set equivalent to the negation of the original formula. Proving the theorem for
$\Pi ^{pc}_\alpha $
set equivalent to the negation of the original formula. Proving the theorem for
![]() $\Sigma ^{pc}_\alpha $
sets directly seems to be difficult using our forcing as for
$\Sigma ^{pc}_\alpha $
sets directly seems to be difficult using our forcing as for
![]() $\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formulas
$\mathbb {N}\mbox {-}\Sigma ^{pc}_\alpha $
formulas
![]() $\xi $
,
$\xi $
,
![]() $\emptyset \not \Vdash _{\mathcal {A}} \xi $
.
$\emptyset \not \Vdash _{\mathcal {A}} \xi $
.
Theorem 3.12. Fix a computable ordinal
![]() $\alpha \geq 1$
. An isomorphism invariant
$\alpha \geq 1$
. An isomorphism invariant
![]() $B\subseteq Mod(\tau )$
is
$B\subseteq Mod(\tau )$
is
![]() $\Pi ^0_\alpha $
if and only if there is a
$\Pi ^0_\alpha $
if and only if there is a
![]() $\Pi ^{pc}_\alpha $
$\Pi ^{pc}_\alpha $
![]() $\tau $
-sentence
$\tau $
-sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $B=Mod(\varphi )$
.
$B=Mod(\varphi )$
.
Proof The left to right direction is just Theorem 3.11 with
![]() $\mathcal {K}=Mod(\tau )$
. The right to left direction is established by an easy transfinite induction.
$\mathcal {K}=Mod(\tau )$
. The right to left direction is established by an easy transfinite induction.
The following corollary follows directly from the relativization of Theorem 3.12 after one notices that every
![]() $\pmb\Pi ^0_\alpha $
is
$\pmb\Pi ^0_\alpha $
is
![]() $\Pi ^0_\alpha (X)$
for some
$\Pi ^0_\alpha (X)$
for some
![]() $X\subseteq \omega $
.
$X\subseteq \omega $
.
Corollary 3.13. Let
![]() $B \subseteq \text {Mod}(\mathcal {L})$
be isomorphism invariant and let
$B \subseteq \text {Mod}(\mathcal {L})$
be isomorphism invariant and let
![]() $\alpha \geq 1$
. The set B is
$\alpha \geq 1$
. The set B is
![]() $\pmb\Pi ^0_\alpha $
if and only if there is a
$\pmb\Pi ^0_\alpha $
if and only if there is a
![]() $\Pi ^p_\alpha $
sentence
$\Pi ^p_\alpha $
sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $B = \text {Mod}(\varphi )$
.
$B = \text {Mod}(\varphi )$
.
By the argument given after Theorem 3.11 the analogs of Theorem 3.12 and Corollary 3.13 for
![]() $\pmb\Sigma ^0_\alpha $
sets are also true.
$\pmb\Sigma ^0_\alpha $
sets are also true.
4 A pullback theorem for computable embeddings
An enumeration operator
![]() $\Gamma $
is a c.e. set of pairs
$\Gamma $
is a c.e. set of pairs
![]() $\langle n, m\rangle $
where we treat n as an index for
$\langle n, m\rangle $
where we treat n as an index for
![]() $F_n$
, the nth set in a fixed computable enumeration of the finite subsets of
$F_n$
, the nth set in a fixed computable enumeration of the finite subsets of
![]() $\omega $
. For
$\omega $
. For
![]() $X\subseteq \omega $
we write
$X\subseteq \omega $
we write
![]() $\Gamma (X)$
for the set
$\Gamma (X)$
for the set
![]() $\{m: \langle n,m\rangle \in \Gamma \text { and } F_n\subseteq X\}$
, and for an element
$\{m: \langle n,m\rangle \in \Gamma \text { and } F_n\subseteq X\}$
, and for an element
![]() $f \in 2^\omega $
, we let
$f \in 2^\omega $
, we let
![]() $X_f\subseteq \omega $
be such that
$X_f\subseteq \omega $
be such that
![]() $\chi _{X_f}=f$
. Then an enumeration operator
$\chi _{X_f}=f$
. Then an enumeration operator
![]() $\Gamma $
defines a function
$\Gamma $
defines a function
![]() $2^\omega \to 2^\omega $
given by
$2^\omega \to 2^\omega $
given by
![]() $f\mapsto \chi _{\Gamma (X_f)}$
. In fact, it is easy to see that enumeration operators are Scott continuous (i.e., continuous functions in the Scott topology on
$f\mapsto \chi _{\Gamma (X_f)}$
. In fact, it is easy to see that enumeration operators are Scott continuous (i.e., continuous functions in the Scott topology on
![]() $2^\omega $
). Identifying countable models in relational vocabularies by their atomic diagrams, we may view enumeration operators as Scott continuous functions from
$2^\omega $
). Identifying countable models in relational vocabularies by their atomic diagrams, we may view enumeration operators as Scott continuous functions from
![]() $Mod(\tau _0)$
to
$Mod(\tau _0)$
to
![]() $Mod(\tau _1)$
for
$Mod(\tau _1)$
for
![]() $\tau _0,\tau _1$
relational vocabularies, and, thus, as functions between classes of structures.
$\tau _0,\tau _1$
relational vocabularies, and, thus, as functions between classes of structures.
Let
![]() $\mathcal {K}_0$
be a class of
$\mathcal {K}_0$
be a class of
![]() $\tau _0$
-structures, and let
$\tau _0$
-structures, and let
![]() $\mathcal {K}_1$
be a class of
$\mathcal {K}_1$
be a class of
![]() $\tau _1$
-structures.
$\tau _1$
-structures.
Definition 4.1. An enumeration operator
![]() $\Gamma $
is a positive computable embedding of
$\Gamma $
is a positive computable embedding of
![]() $\mathcal {K}_0$
into
$\mathcal {K}_0$
into
![]() $\mathcal {K}_1$
, denoted by
$\mathcal {K}_1$
, denoted by
![]() $\Gamma \colon \mathcal {K}_0 \leq _{pc} \mathcal {K}_1$
, if
$\Gamma \colon \mathcal {K}_0 \leq _{pc} \mathcal {K}_1$
, if
![]() $\Gamma $
satisfies the following:
$\Gamma $
satisfies the following:
-
(1) For any
 $\mathcal {A}\in \mathcal {K}_0$
,
$\mathcal {A}\in \mathcal {K}_0$
,
 $\Gamma (D(\mathcal {A}))$
is the atomic diagram of a structure from
$\Gamma (D(\mathcal {A}))$
is the atomic diagram of a structure from
 $\mathcal {K}_1$
. This structure is denoted by
$\mathcal {K}_1$
. This structure is denoted by
 $\Gamma (\mathcal {A})$
.
$\Gamma (\mathcal {A})$
. -
(2) For any
 $\mathcal {A},\mathcal {B}\in \mathcal {K}_0$
, we have
$\mathcal {A},\mathcal {B}\in \mathcal {K}_0$
, we have
 $\mathcal {A}\cong \mathcal {B}$
if and only if
$\mathcal {A}\cong \mathcal {B}$
if and only if
 $\Gamma (\mathcal {A}) \cong \Gamma (\mathcal {B})$
.
$\Gamma (\mathcal {A}) \cong \Gamma (\mathcal {B})$
.
Positive computable embeddings have the useful property of monotonicity: If
![]() $\Gamma \colon \mathcal {K}_0 \leq _{pc} \mathcal {K}_1$
and
$\Gamma \colon \mathcal {K}_0 \leq _{pc} \mathcal {K}_1$
and
![]() $\mathcal {A}\subseteq \mathcal {B}$
are structures from
$\mathcal {A}\subseteq \mathcal {B}$
are structures from
![]() $\mathcal {K}_0$
, then we have
$\mathcal {K}_0$
, then we have
![]() $\Gamma (\mathcal {A}) \subseteq \Gamma (\mathcal {B})$
.
$\Gamma (\mathcal {A}) \subseteq \Gamma (\mathcal {B})$
.
For total structures, i.e., structures of the form
![]() $\mathcal {A} = (A, R_1,\dots ,R_n, \overline {R}_1,\dots ,\overline {R}_n)$
, the notion of positive computable embedding coincides with the notion of computable embedding as defined in [Reference Knight, Miller and Vanden Boom23] and denoted by
$\mathcal {A} = (A, R_1,\dots ,R_n, \overline {R}_1,\dots ,\overline {R}_n)$
, the notion of positive computable embedding coincides with the notion of computable embedding as defined in [Reference Knight, Miller and Vanden Boom23] and denoted by
![]() $\leq _c$
.
$\leq _c$
.
Let us denote the structure
![]() $\mathcal {A}_X = (\mathbb {N}, S, X)$
, where S is the successor relation and X is an arbitrary set. Then it is clear that
$\mathcal {A}_X = (\mathbb {N}, S, X)$
, where S is the successor relation and X is an arbitrary set. Then it is clear that
![]() $\{\mathcal {A}_{K}\} \leq _c \{\mathcal {A}_{\overline {K}}\}$
, but
$\{\mathcal {A}_{K}\} \leq _c \{\mathcal {A}_{\overline {K}}\}$
, but
![]() $\{\mathcal {A}_{K}\} \not \leq _{pc} \{\mathcal {A}_{\overline {K}}\}$
, where K denotes the halting set. Moreover,
$\{\mathcal {A}_{K}\} \not \leq _{pc} \{\mathcal {A}_{\overline {K}}\}$
, where K denotes the halting set. Moreover,
![]() $\{\mathcal {A}_\emptyset \} \leq _{pc} \{\mathcal {A}_K\}$
, but
$\{\mathcal {A}_\emptyset \} \leq _{pc} \{\mathcal {A}_K\}$
, but
![]() $\{\mathcal {A}_\emptyset \} \not \leq _c \{\mathcal {A}_K\}$
.
$\{\mathcal {A}_\emptyset \} \not \leq _c \{\mathcal {A}_K\}$
.
Definition 4.2 [Reference Knight, Miller and Vanden Boom23].
A Turing operator
![]() $\Phi =\varphi _e$
is a Turing computable embedding of
$\Phi =\varphi _e$
is a Turing computable embedding of
![]() $\mathcal {K}_0$
into
$\mathcal {K}_0$
into
![]() $\mathcal {K}_1$
, denoted by
$\mathcal {K}_1$
, denoted by
![]() $\Phi \colon \mathcal {K}_0 \leq _{tc} \mathcal {K}_1$
, if
$\Phi \colon \mathcal {K}_0 \leq _{tc} \mathcal {K}_1$
, if
![]() $\Phi $
satisfies the following:
$\Phi $
satisfies the following:
-
(1) For any
 $\mathcal {A}\in \mathcal {K}_0$
, the function
$\mathcal {A}\in \mathcal {K}_0$
, the function
 $\varphi ^{D(\mathcal {A})}_e$
is the characteristic function of the atomic diagram of a structure from
$\varphi ^{D(\mathcal {A})}_e$
is the characteristic function of the atomic diagram of a structure from
 $\mathcal {K}_1$
. This structure is denoted by
$\mathcal {K}_1$
. This structure is denoted by
 $\Phi (\mathcal {A})$
.
$\Phi (\mathcal {A})$
. -
(2) For any
 $\mathcal {A},\mathcal {B}\in \mathcal {K}_0$
, we have
$\mathcal {A},\mathcal {B}\in \mathcal {K}_0$
, we have
 $\mathcal {A}\cong \mathcal {B}$
if and only if
$\mathcal {A}\cong \mathcal {B}$
if and only if
 $\Phi (\mathcal {A}) \cong \Phi (\mathcal {B})$
.
$\Phi (\mathcal {A}) \cong \Phi (\mathcal {B})$
.
Turing computable embeddings do in general not have the monotonicity properties of computable embeddings. This can be used to show the following.
Proposition 4.3 (Greenberg and, independently, Kalimullin; see [Reference Kalimullin20, Reference Knight, Miller and Vanden Boom23]).
If
![]() $\mathcal {K}_0 \leq _c \mathcal {K}_1$
, then
$\mathcal {K}_0 \leq _c \mathcal {K}_1$
, then
![]() $\mathcal {K}_0 \leq _{tc} \mathcal {K}_1$
. The converse is not true.
$\mathcal {K}_0 \leq _{tc} \mathcal {K}_1$
. The converse is not true.
The Pullback Theorem in [Reference Vanden Boom4] connects Turing computable embeddings with definability by classical computable infinitary sentences. We obtain an analog of this result in our setting. The original pullback theorem was proved for structures whose universe can be arbitrary subsets of the natural numbers. Our version might seem a bit more restrictive at first sight, as we assume the universes of our structures to be
![]() $\omega $
and this in particular excludes finite structures. However, we could easily add unary relations for the universe of a structure and its coset to the vocabulary and then we could deal with this more general setting as well.
$\omega $
and this in particular excludes finite structures. However, we could easily add unary relations for the universe of a structure and its coset to the vocabulary and then we could deal with this more general setting as well.
Proposition 4.4. A positive computable embedding
![]() $\Gamma _e:\mathcal {K}\leq _{pc}\mathcal {K}'$
can be transformed into an effective Scott continuous function
$\Gamma _e:\mathcal {K}\leq _{pc}\mathcal {K}'$
can be transformed into an effective Scott continuous function
![]() $\Gamma _a:\text {Mod}(\tau )\to \text {Mod}(\tau ')$
with the property that
$\Gamma _a:\text {Mod}(\tau )\to \text {Mod}(\tau ')$
with the property that
![]() $\Gamma _a(\mathcal {K})=\Gamma _e(\mathcal {K})$
.
$\Gamma _a(\mathcal {K})=\Gamma _e(\mathcal {K})$
.
Proof Recall that for a set A,
![]() $\Gamma _e(A) = \{x \mid \langle {v,x}\rangle \in W_e\ \&\ D_v \subseteq A\}$
. We may suppose that for all natural numbers n,
$\Gamma _e(A) = \{x \mid \langle {v,x}\rangle \in W_e\ \&\ D_v \subseteq A\}$
. We may suppose that for all natural numbers n,
![]() $\langle {\ulcorner {\emptyset }\urcorner ,\ulcorner {n=n}\urcorner }\rangle \in W_e$
. This ensures that all output sets can be interpreted as
$\langle {\ulcorner {\emptyset }\urcorner ,\ulcorner {n=n}\urcorner }\rangle \in W_e$
. This ensures that all output sets can be interpreted as
![]() $\tau '$
-structures with domains
$\tau '$
-structures with domains
![]() $\omega $
. Since we can interpret any natural number as the code of a positive atomic sentence in
$\omega $
. Since we can interpret any natural number as the code of a positive atomic sentence in
![]() $\tau '$
, we only need to filter out from
$\tau '$
, we only need to filter out from
![]() $W_e$
all sentences of the form
$W_e$
all sentences of the form
![]() $n \neq n$
and
$n \neq n$
and
![]() $n = m$
for different natural numbers n and m.
$n = m$
for different natural numbers n and m.
Let us have the enumeration
![]() $\{W_{e,s}\}_{s<\omega }$
of the c.e. set
$\{W_{e,s}\}_{s<\omega }$
of the c.e. set
![]() $W_e$
, where
$W_e$
, where
![]() $W_e = \bigcup _s W_{e,s}$
,
$W_e = \bigcup _s W_{e,s}$
,
![]() $W_{e,0} = \emptyset $
, and
$W_{e,0} = \emptyset $
, and
![]() $|W_{e,s+1}\setminus W_{e,s}| \leq 1$
for all s. We define
$|W_{e,s+1}\setminus W_{e,s}| \leq 1$
for all s. We define
![]() $W_{a,s}$
inductively so that
$W_{a,s}$
inductively so that
![]() $W_{a,0} = \emptyset $
and
$W_{a,0} = \emptyset $
and
![]() $W_{a,s+1} = W_{a,s}$
if
$W_{a,s+1} = W_{a,s}$
if
![]() $\langle {v,\ulcorner {n\neq n}\urcorner }\rangle $
or
$\langle {v,\ulcorner {n\neq n}\urcorner }\rangle $
or
![]() $\langle {v,\ulcorner {n=m}\urcorner }\rangle $
belongs to
$\langle {v,\ulcorner {n=m}\urcorner }\rangle $
belongs to
![]() $W_{e,s+1}\setminus W_{e,s}$
, and otherwise, set
$W_{e,s+1}\setminus W_{e,s}$
, and otherwise, set
![]() $W_{a,s+1} = W_{a,s} \cup (W_{e,s+1}\setminus W_{e,s})$
. Then clearly
$W_{a,s+1} = W_{a,s} \cup (W_{e,s+1}\setminus W_{e,s})$
. Then clearly
![]() $\Gamma _a:\text {Mod}(\tau ) \to \text {Mod}(\tau ')$
is an effective Scott continuous mapping and by the construction of
$\Gamma _a:\text {Mod}(\tau ) \to \text {Mod}(\tau ')$
is an effective Scott continuous mapping and by the construction of
![]() $W_a$
,
$W_a$
,
![]() $\Gamma _a(\mathcal {K}) = \Gamma _e(\mathcal {K})$
. It is clear that we can effectively obtain the index a from the index e.
$\Gamma _a(\mathcal {K}) = \Gamma _e(\mathcal {K})$
. It is clear that we can effectively obtain the index a from the index e.
Theorem 4.5 (Pullback Theorem).
Let
![]() $\mathcal {K} \subseteq \text {Mod}(\tau )$
and
$\mathcal {K} \subseteq \text {Mod}(\tau )$
and
![]() $\mathcal {K}' \subseteq \text {Mod}(\tau ')$
be closed under isomorphism. Let
$\mathcal {K}' \subseteq \text {Mod}(\tau ')$
be closed under isomorphism. Let
![]() $\Gamma _e : \mathcal {K} \leq _{pc} \mathcal {K}'$
, then for any
$\Gamma _e : \mathcal {K} \leq _{pc} \mathcal {K}'$
, then for any
![]() $L^{pc}_{\omega _1\omega }$
$L^{pc}_{\omega _1\omega }$
![]() $\tau '$
-sentence
$\tau '$
-sentence
![]() $\varphi '$
we can effectively find an
$\varphi '$
we can effectively find an
![]() $L^{pc}_{\omega _1\omega }$
$L^{pc}_{\omega _1\omega }$
![]() $\tau $
-sentence
$\tau $
-sentence
![]() $\varphi $
such that for all
$\varphi $
such that for all
![]() $\mathcal {A} \in \mathcal {K}$
,
$\mathcal {A} \in \mathcal {K}$
,
Moreover, if
![]() $\varphi '$
is
$\varphi '$
is
![]() $\Sigma ^{pc}_\alpha $
(or
$\Sigma ^{pc}_\alpha $
(or
![]() $\Pi ^{pc}_\alpha $
), then so is
$\Pi ^{pc}_\alpha $
), then so is
![]() $\varphi $
.
$\varphi $
.
Proof By Proposition 4.4, we can view
![]() $\Gamma _e$
as an effective Scott continuous function from
$\Gamma _e$
as an effective Scott continuous function from
![]() $\text {Mod}(\tau )$
to
$\text {Mod}(\tau )$
to
![]() $\text {Mod}(\tau ')$
that is isomorphism invariant on
$\text {Mod}(\tau ')$
that is isomorphism invariant on
![]() $\mathcal {K}$
, i.e.,
$\mathcal {K}$
, i.e.,
![]() $\mathcal {A} \cong \mathcal {B}$
if and only if
$\mathcal {A} \cong \mathcal {B}$
if and only if
![]() $\Gamma _e(\mathcal {A})\cong \Gamma _e(\mathcal {B})$
for all
$\Gamma _e(\mathcal {A})\cong \Gamma _e(\mathcal {B})$
for all
![]() $\mathcal {A},\mathcal {B}\in \mathcal {K}$
. Thus if
$\mathcal {A},\mathcal {B}\in \mathcal {K}$
. Thus if
![]() $B\subseteq Mod(\tau ')$
is invariant
$B\subseteq Mod(\tau ')$
is invariant
![]() $\pmb\Pi ^0_\alpha $
, then
$\pmb\Pi ^0_\alpha $
, then
![]() $\Gamma _e^{-1}(B)$
is a
$\Gamma _e^{-1}(B)$
is a
![]() $\pmb\Pi ^0_\alpha $
subset of
$\pmb\Pi ^0_\alpha $
subset of
![]() $Mod(\tau )$
that is invariant on
$Mod(\tau )$
that is invariant on
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
The
![]() $\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula
$\mathbb {N}\mbox {-}\Pi ^p_\alpha $
formula
![]() $\xi $
describing
$\xi $
describing
![]() $\Gamma _e^{-1}(B)$
can be effectively obtained from
$\Gamma _e^{-1}(B)$
can be effectively obtained from
![]() $\xi '$
corresponding to B by replacing occurrences of atomic formulas in
$\xi '$
corresponding to B by replacing occurrences of atomic formulas in
![]() $\xi '$
with the following formulas depending on their type:
$\xi '$
with the following formulas depending on their type:
An easy induction shows that
![]() $\xi \in \Pi ^p_\alpha $
if and only if
$\xi \in \Pi ^p_\alpha $
if and only if
![]() $\xi '\in \Pi ^p_\alpha $
for
$\xi '\in \Pi ^p_\alpha $
for
![]() $\alpha>1$
and that
$\alpha>1$
and that
![]() $Mod(\xi )=\Gamma _e^{-1}(\xi ')$
. We obtained
$Mod(\xi )=\Gamma _e^{-1}(\xi ')$
. We obtained
![]() $\xi $
effectively from
$\xi $
effectively from
![]() $\xi '$
. Thus, if
$\xi '$
. Thus, if
![]() $B=Mod(\xi ')$
is
$B=Mod(\xi ')$
is
![]() $\Pi ^0_\alpha $
, so is
$\Pi ^0_\alpha $
, so is
![]() $\Gamma _e^{-1}(B)=Mod(\xi )$
. A similar argument works for
$\Gamma _e^{-1}(B)=Mod(\xi )$
. A similar argument works for
![]() $\Sigma ^p_\alpha $
formulas. To complete the proof of the theorem use Theorem 3.12 to obtain
$\Sigma ^p_\alpha $
formulas. To complete the proof of the theorem use Theorem 3.12 to obtain
![]() $\xi '$
from
$\xi '$
from
![]() $\varphi '$
and then use Theorem 3.11 to obtain
$\varphi '$
and then use Theorem 3.11 to obtain
![]() $\varphi $
from
$\varphi $
from
![]() $\xi $
such that
$\xi $
such that
![]() $Mod(\varphi )$
is equal to
$Mod(\varphi )$
is equal to
![]() $\Gamma _e^{-1}(B)$
within
$\Gamma _e^{-1}(B)$
within
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
5 An application
In this section, we give a simple application of the Pullback theorem which illuminates the difference between Turing and enumeration operators.
Definition 5.1 [Reference Ganchev, Kalimullin and Vatev16].
For a structure
![]() $\mathcal {A}$
, let
$\mathcal {A}$
, let
![]() $\tilde {\mathcal {A}}$
be a structure with a new congruence relation
$\tilde {\mathcal {A}}$
be a structure with a new congruence relation
![]() $\sim $
such that:
$\sim $
such that:
-
a) the
 $\sim $
-class for each element in
$\sim $
-class for each element in
 $\tilde {\mathcal {A}}$
is infinite;
$\tilde {\mathcal {A}}$
is infinite; -
b)
 $\tilde {\mathcal {A}}/_{\sim } \cong \mathcal {A}$
.
$\tilde {\mathcal {A}}/_{\sim } \cong \mathcal {A}$
.
For a class
![]() $\mathcal {K}$
, let
$\mathcal {K}$
, let
![]() $\tilde {\mathcal {K}} = \{\tilde {\mathcal {A}} \mid \mathcal {A} \in \mathcal {K}\}$
.
$\tilde {\mathcal {K}} = \{\tilde {\mathcal {A}} \mid \mathcal {A} \in \mathcal {K}\}$
.
Intuitively, if
![]() $\mathcal {K}$
is in a relational vocabulary, then the isomorphism types in the class
$\mathcal {K}$
is in a relational vocabulary, then the isomorphism types in the class
![]() $\tilde {\mathcal {K}}$
are obtained from
$\tilde {\mathcal {K}}$
are obtained from
![]() $\mathcal {K}$
by replacing each element a in the universe of
$\mathcal {K}$
by replacing each element a in the universe of
![]() $\mathcal {A}\in \mathcal {K}$
by infinitely many elements
$\mathcal {A}\in \mathcal {K}$
by infinitely many elements
![]() $(i_a)_{i\in \omega }$
and introducing a binary relation
$(i_a)_{i\in \omega }$
and introducing a binary relation
![]() $\sim $
to the language such that
$\sim $
to the language such that
![]() $i_x\sim i_y$
if and only if
$i_x\sim i_y$
if and only if
![]() $x=y$
. For example, if we are given an order type
$x=y$
. For example, if we are given an order type
![]() $\mathcal L$
, then
$\mathcal L$
, then
![]() $\tilde {\mathcal L}$
is a quasi-order with
$\tilde {\mathcal L}$
is a quasi-order with
![]() $x\sim y$
if and only if
$x\sim y$
if and only if
![]() $x\leq y$
and
$x\leq y$
and
![]() $y\leq x$
where each
$y\leq x$
where each
![]() $\sim $
-class is infinite.
$\sim $
-class is infinite.
It is not difficult to see that we always have
![]() $\tilde {\mathcal {K}} \equiv _{tc} \mathcal {K}$
,
$\tilde {\mathcal {K}} \equiv _{tc} \mathcal {K}$
,
![]() $\mathcal {K} \leq _c \tilde {\mathcal {K}}$
, and
$\mathcal {K} \leq _c \tilde {\mathcal {K}}$
, and
![]() $\tilde {\tilde {\mathcal {K}}} \leq _c \tilde {\mathcal {K}}$
. More generally, for any two classes of structures
$\tilde {\tilde {\mathcal {K}}} \leq _c \tilde {\mathcal {K}}$
. More generally, for any two classes of structures
![]() $\mathcal {K}_0$
and
$\mathcal {K}_0$
and
![]() $\mathcal {K}_1$
, we have the following implications:
$\mathcal {K}_1$
, we have the following implications:
We will give examples of classes of linear orderings such that the converse of these implications does not hold. Let
![]() $\mathbf n$
denote the finite order type of size n for
$\mathbf n$
denote the finite order type of size n for
![]() $n\in \omega $
, and given any preorder
$n\in \omega $
, and given any preorder
![]() $\mathcal {A}$
, let
$\mathcal {A}$
, let
![]() $\mathcal {A}^{\star }$
be the structure obtained by reversing the order, i.e., if
$\mathcal {A}^{\star }$
be the structure obtained by reversing the order, i.e., if
![]() $x\leq ^{\mathcal {A}} y$
, then
$x\leq ^{\mathcal {A}} y$
, then
![]() $y\leq ^{\mathcal {A}^{\star }}x$
. To see that the second implication is strict consider the classes
$y\leq ^{\mathcal {A}^{\star }}x$
. To see that the second implication is strict consider the classes
![]() $\mathcal {K}_0 = \{\mathbf {1}, \mathbf {2}\}$
and
$\mathcal {K}_0 = \{\mathbf {1}, \mathbf {2}\}$
and
![]() $\mathcal {K}_1 = \{\omega ,\omega ^{\star }\}$
. It is easy to see that
$\mathcal {K}_1 = \{\omega ,\omega ^{\star }\}$
. It is easy to see that
![]() $\mathcal {K}_0 \leq _{tc} \mathcal {K}_1$
, but the monotonicity of enumeration operators gives us that
$\mathcal {K}_0 \leq _{tc} \mathcal {K}_1$
, but the monotonicity of enumeration operators gives us that
![]() $\tilde {\mathcal {K}}_0 \not \leq _{c} \tilde {\mathcal {K}}_1$
because
$\tilde {\mathcal {K}}_0 \not \leq _{c} \tilde {\mathcal {K}}_1$
because
![]() $\tilde {\mathbf {1}}$
is a substructure of
$\tilde {\mathbf {1}}$
is a substructure of
![]() $\tilde {\mathbf {2}}$
, but
$\tilde {\mathbf {2}}$
, but
![]() $\tilde {\omega }$
is not a substructure of
$\tilde {\omega }$
is not a substructure of
![]() $\tilde {\omega }^{\star }$
.
$\tilde {\omega }^{\star }$
.
Kalimullin [Reference Ganchev, Kalimullin and Vatev16] built a class
![]() $\mathcal {K}$
of finite undirected graphs such that
$\mathcal {K}$
of finite undirected graphs such that
![]() $\tilde {\mathcal {K}} \not \leq _c \mathcal {K}$
. This shows that the first implication is strict as we always have
$\tilde {\mathcal {K}} \not \leq _c \mathcal {K}$
. This shows that the first implication is strict as we always have
![]() $\tilde {\tilde {\mathcal {K}}} \leq _c \tilde {\mathcal {K}}$
. Since the example in the class of graphs is somewhat artificial, Kalimullin asked the following question.
$\tilde {\tilde {\mathcal {K}}} \leq _c \tilde {\mathcal {K}}$
. Since the example in the class of graphs is somewhat artificial, Kalimullin asked the following question.
Question 5.2 (Kalimullin).
Are there natural classes of structures
![]() $\mathcal {K}$
such that
$\mathcal {K}$
such that
Theorem 5.3 (Ganchev–Kalimullin–Vatev [Reference Ganchev, Kalimullin and Vatev16]).
Let
![]() $\mathcal {K} = \{\omega _S,\omega ^{\star }_S\}$
be the class of strict linear orderings of types
$\mathcal {K} = \{\omega _S,\omega ^{\star }_S\}$
be the class of strict linear orderings of types
![]() $\omega $
and
$\omega $
and
![]() $\omega ^{\star }$
, equipped with the successor relation. Then
$\omega ^{\star }$
, equipped with the successor relation. Then
![]() $\tilde {\mathcal {K}} \not \leq _{c} \mathcal {K}$
.
$\tilde {\mathcal {K}} \not \leq _{c} \mathcal {K}$
.
Interestingly, it is not known whether
![]() $\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{c} \{\omega ,\omega ^{\star }\}$
, where
$\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{c} \{\omega ,\omega ^{\star }\}$
, where
![]() $\{\omega , \omega ^{\star }\}$
is the class of strict linear orderings of types
$\{\omega , \omega ^{\star }\}$
is the class of strict linear orderings of types
![]() $\omega $
and
$\omega $
and
![]() $\omega ^{\star }$
. Nevertheless, if we let
$\omega ^{\star }$
. Nevertheless, if we let
![]() $\{\omega ,\omega ^{\star }\}$
be the class of linear orderings of order type
$\{\omega ,\omega ^{\star }\}$
be the class of linear orderings of order type
![]() $\omega $
and
$\omega $
and
![]() $\omega ^{\star }$
in the vocabulary
$\omega ^{\star }$
in the vocabulary
![]() $\leq , =, \neq $
, then we can apply our new version of the Pullback Theorem and show that
$\leq , =, \neq $
, then we can apply our new version of the Pullback Theorem and show that
![]() $\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{pc} \{\omega ,\omega ^{\star }\}$
. For
$\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{pc} \{\omega ,\omega ^{\star }\}$
. For
![]() $\mathcal {A}$
a linear ordering, the congruence relation
$\mathcal {A}$
a linear ordering, the congruence relation
![]() $x \sim y$
in
$x \sim y$
in
![]() $\tilde {\mathcal {A}}$
is definable by the
$\tilde {\mathcal {A}}$
is definable by the
![]() $\Sigma ^p_0$
formula
$\Sigma ^p_0$
formula
![]() $x \leq y \land y \leq x$
, and, thus, we may omit
$x \leq y \land y \leq x$
, and, thus, we may omit
![]() $\sim $
from the vocabulary.
$\sim $
from the vocabulary.
For a class of formulas
![]() $\mathcal {C}$
(e.g.,
$\mathcal {C}$
(e.g.,
![]() $\Sigma ^p_0$
and
$\Sigma ^p_0$
and
![]() $\Pi ^p_1$
), a structure
$\Pi ^p_1$
), a structure
![]() $\mathcal {A}$
, and a tuple
$\mathcal {A}$
, and a tuple
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\mathcal {A}$
, define
$\mathcal {A}$
, define
![]() $\mathcal {C}\text {-}Th_{\mathcal {A}}(\bar {a}) = \{\xi (\bar {x}) \in \mathcal {C} \mid \mathcal {A} \models \xi (\bar {a})\}$
. If the tuple
$\mathcal {C}\text {-}Th_{\mathcal {A}}(\bar {a}) = \{\xi (\bar {x}) \in \mathcal {C} \mid \mathcal {A} \models \xi (\bar {a})\}$
. If the tuple
![]() $\bar {a}$
is empty, we will write
$\bar {a}$
is empty, we will write
![]() $\mathcal {C}\text {-}Th_{\mathcal {A}}$
.
$\mathcal {C}\text {-}Th_{\mathcal {A}}$
.
The next proposition isolates the key property that the class
![]() $\{\tilde {\omega }, \tilde {\omega }^{\star }\}$
possess which will allow us to show that
$\{\tilde {\omega }, \tilde {\omega }^{\star }\}$
possess which will allow us to show that
![]() $\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{pc} \{\omega ,\omega ^{\star }\}$
.
$\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{pc} \{\omega ,\omega ^{\star }\}$
.
Proposition 5.4. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be linear orderings in the vocabulary
$\mathcal {B}$
be linear orderings in the vocabulary
![]() $\leq , =, \neq $
. For any tuple
$\leq , =, \neq $
. For any tuple
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\tilde {\mathcal {A}}$
and any tuple
$\tilde {\mathcal {A}}$
and any tuple
![]() $\bar {b}$
in
$\bar {b}$
in
![]() $\tilde {\mathcal {B}}$
, if
$\tilde {\mathcal {B}}$
, if
![]() $\Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
, then
$\Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
, then
![]() $\Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
.
$\Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
.
Proof It is enough to show that
![]() $\Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) \subseteq \Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
. Consider a formula
$\Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) \subseteq \Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
. Consider a formula ![]() , where
, where
![]() $\xi _i(\bar {x},\bar {x}_i)$
are
$\xi _i(\bar {x},\bar {x}_i)$
are
![]() $\Sigma ^{pc}_0$
. Suppose
$\Sigma ^{pc}_0$
. Suppose
![]() $\tilde {\mathcal {A}} \models \varphi (\bar {a})$
. Fix
$\tilde {\mathcal {A}} \models \varphi (\bar {a})$
. Fix
![]() $i \in W_e$
and a tuple
$i \in W_e$
and a tuple
![]() $\bar {a}'$
in
$\bar {a}'$
in
![]() $\tilde {A}$
such that
$\tilde {A}$
such that
![]() $\tilde {\mathcal {A}} \models \xi _i(\bar {a},\bar {a}')$
.
$\tilde {\mathcal {A}} \models \xi _i(\bar {a},\bar {a}')$
.
Since
![]() $\Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
, we know that
$\Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
, we know that
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
are ordered in the same way. Without loss of generality, suppose
$\bar {b}$
are ordered in the same way. Without loss of generality, suppose
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
have length n and
$\bar {b}$
have length n and
![]() $\tilde {\mathcal {A}} \models a_0 \leq a_1 \leq \cdots \leq a_{n-1}$
and similarly,
$\tilde {\mathcal {A}} \models a_0 \leq a_1 \leq \cdots \leq a_{n-1}$
and similarly,
![]() $\tilde {\mathcal {B}} \models b_0 \leq b_1 \leq \cdots \leq b_{n-1}$
. We consider two cases which show how we find the tuple
$\tilde {\mathcal {B}} \models b_0 \leq b_1 \leq \cdots \leq b_{n-1}$
. We consider two cases which show how we find the tuple
![]() $\bar {b}'$
which makes
$\bar {b}'$
which makes
![]() $\xi _i(\bar {b},\bar {b}')$
true in
$\xi _i(\bar {b},\bar {b}')$
true in
![]() $\tilde {\mathcal {B}}$
. In both cases we use the fact that each
$\tilde {\mathcal {B}}$
. In both cases we use the fact that each
![]() $\sim $
-class is infinite.
$\sim $
-class is infinite.
Suppose that for some
![]() $a^{\prime }_j$
from the tuple
$a^{\prime }_j$
from the tuple
![]() $\bar {a}'$
,
$\bar {a}'$
,
![]() $\tilde {\mathcal {A}} \models a_i \leq a^{\prime }_j \leq a_{i+1}$
. The interesting case is when
$\tilde {\mathcal {A}} \models a_i \leq a^{\prime }_j \leq a_{i+1}$
. The interesting case is when
![]() $a^{\prime }_j$
is in a separate
$a^{\prime }_j$
is in a separate
![]() $\sim $
-class from
$\sim $
-class from
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
, but
$a_{i+1}$
, but
![]() $b_{i+1}$
belongs to the successor
$b_{i+1}$
belongs to the successor
![]() $\sim $
-class of
$\sim $
-class of
![]() $b_{i}$
in
$b_{i}$
in
![]() $\tilde {\mathcal {B}}$
. Then we choose the corresponding element
$\tilde {\mathcal {B}}$
. Then we choose the corresponding element
![]() $b^{\prime }_j$
as an element
$b^{\prime }_j$
as an element
![]() $\sim $
-equivalent to
$\sim $
-equivalent to
![]() $b_i$
or
$b_i$
or
![]() $b_{i+1}$
. In this way,
$b_{i+1}$
. In this way,
![]() $\tilde {\mathcal {B}} \models b_{i} \leq b^{\prime }_j \leq b_{i+1}$
.
$\tilde {\mathcal {B}} \models b_{i} \leq b^{\prime }_j \leq b_{i+1}$
.
Similarly, suppose that for some
![]() $a^{\prime }_j$
from the tuple
$a^{\prime }_j$
from the tuple
![]() $\bar {a}'$
,
$\bar {a}'$
,
![]() $\tilde {\mathcal {A}} \models a_{n-1} \leq a^{\prime }_j$
, but
$\tilde {\mathcal {A}} \models a_{n-1} \leq a^{\prime }_j$
, but
![]() $b_{n-1}$
belongs to the
$b_{n-1}$
belongs to the
![]() $\leq $
-greatest
$\leq $
-greatest
![]() $\sim $
-class in
$\sim $
-class in
![]() $\tilde {\mathcal {B}}$
. Then, again, we choose the corresponding
$\tilde {\mathcal {B}}$
. Then, again, we choose the corresponding
![]() $b^{\prime }_j$
as an element
$b^{\prime }_j$
as an element
![]() $\sim $
-equivalent to
$\sim $
-equivalent to
![]() $b_{n-1}$
.
$b_{n-1}$
.
Notice that Proposition 5.4 does not hold if we consider strict linear orderings
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
and it does not hold for the class
$\mathcal {B}$
and it does not hold for the class
![]() $\{\tilde {\omega }, \tilde {\omega }^{\star }\}$
if the vocabulary under consideration is
$\{\tilde {\omega }, \tilde {\omega }^{\star }\}$
if the vocabulary under consideration is
![]() $<,=,\neq $
.
$<,=,\neq $
.
Lemma 5.5. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be linear orderings in the vocabulary
$\mathcal {B}$
be linear orderings in the vocabulary
![]() $\leq , =, \neq $
. Then
$\leq , =, \neq $
. Then
Proof It is enough to show that
![]() $\Sigma ^{pc}_2\text {-}Th_{\tilde {\mathcal {A}}} \subseteq \Sigma ^{pc}_2\text {-}Th_{\tilde {\mathcal {B}}}$
. Consider a
$\Sigma ^{pc}_2\text {-}Th_{\tilde {\mathcal {A}}} \subseteq \Sigma ^{pc}_2\text {-}Th_{\tilde {\mathcal {B}}}$
. Consider a
![]() $\Sigma ^{pc}_2$
sentence
$\Sigma ^{pc}_2$
sentence
![]() $\varphi $
such that
$\varphi $
such that
where
![]() $\xi _i(\bar {x}_i)$
and
$\xi _i(\bar {x}_i)$
and
![]() $\psi _i(\bar {x}_i)$
are
$\psi _i(\bar {x}_i)$
are
![]() $\Sigma ^p_1$
formulas. Fix
$\Sigma ^p_1$
formulas. Fix
![]() $i \in W_a$
and a tuple
$i \in W_a$
and a tuple
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\tilde {\mathcal {A}}$
such that
$\tilde {\mathcal {A}}$
such that
![]() $\tilde {\mathcal {A}} \models \xi _i(\bar {a}) \land neg(\psi _i(\bar {a}))$
.
$\tilde {\mathcal {A}} \models \xi _i(\bar {a}) \land neg(\psi _i(\bar {a}))$
.
Since every
![]() $\sim $
-class contains infinitely many elements, it is easy to see that we can choose a tuple
$\sim $
-class contains infinitely many elements, it is easy to see that we can choose a tuple
![]() $\bar {b}$
in
$\bar {b}$
in
![]() $\tilde {\mathcal {B}}$
such that
$\tilde {\mathcal {B}}$
such that
![]() $\Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
. But then by Proposition 5.4,
$\Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_0\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
. But then by Proposition 5.4,
![]() $\Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
. It follows that
$\Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {A}}}(\bar {a}) = \Sigma ^{pc}_1\text {-}Th_{\tilde {\mathcal {B}}}(\bar {b})$
. It follows that
![]() $\tilde {\mathcal {A}} \models \xi _i(\bar {b}) \land neg(\psi _i(\bar {b}))$
and hence
$\tilde {\mathcal {A}} \models \xi _i(\bar {b}) \land neg(\psi _i(\bar {b}))$
and hence
![]() $\tilde {\mathcal {B}} \models \varphi $
.
$\tilde {\mathcal {B}} \models \varphi $
.
Theorem 5.6.
![]() $\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{pc} \{\omega ,\omega ^{\star }\}$
.
$\{\tilde {\omega },\tilde {\omega }^{\star }\} \not \leq _{pc} \{\omega ,\omega ^{\star }\}$
.
Proof Consider the
![]() $\Sigma ^{pc}_2$
sentences
$\Sigma ^{pc}_2$
sentences
and
It is clear that for any two copies
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {A}^{\star }$
of
$\mathcal {A}^{\star }$
of
![]() $\omega $
and
$\omega $
and
![]() $\omega ^{\star }$
, respectively,
$\omega ^{\star }$
, respectively,
![]() $\mathcal {A} \models \varphi _0 \land \neg \varphi _1$
and
$\mathcal {A} \models \varphi _0 \land \neg \varphi _1$
and
![]() $\mathcal {A}^{\star } \models \neg \varphi _0 \land \varphi _1$
. Notice that we don’t use the formulas
$\mathcal {A}^{\star } \models \neg \varphi _0 \land \varphi _1$
. Notice that we don’t use the formulas
![]() $\exists x \forall y(x\leq y)$
and
$\exists x \forall y(x\leq y)$
and
![]() $\exists x \forall y(y \leq x)$
since they are
$\exists x \forall y(y \leq x)$
since they are
![]() $\Sigma ^{pc}_3$
and not
$\Sigma ^{pc}_3$
and not
![]() $\Sigma ^{pc}_2$
.
$\Sigma ^{pc}_2$
.
If we assume that
![]() $\{\tilde {\omega },\tilde {\omega }^{\star }\} \leq _{pc} \{\omega ,\omega ^{\star }\}$
, by the Pullback Theorem, there must be
$\{\tilde {\omega },\tilde {\omega }^{\star }\} \leq _{pc} \{\omega ,\omega ^{\star }\}$
, by the Pullback Theorem, there must be
![]() $\Sigma ^{pc}_2$
sentences
$\Sigma ^{pc}_2$
sentences
![]() $\tilde {\varphi }_0$
and
$\tilde {\varphi }_0$
and
![]() $\tilde {\varphi }_1$
such that for any two copies
$\tilde {\varphi }_1$
such that for any two copies
![]() $\tilde {\mathcal {A}}$
and
$\tilde {\mathcal {A}}$
and
![]() $\tilde {\mathcal {A}}^{\star }$
of
$\tilde {\mathcal {A}}^{\star }$
of
![]() $\tilde {\omega }$
and
$\tilde {\omega }$
and
![]() $\tilde {\omega }^{\star }$
, respectively,
$\tilde {\omega }^{\star }$
, respectively,
![]() $\tilde {\mathcal {A}} \models \tilde {\varphi }_0 \land \neg \tilde {\varphi }_1$
and
$\tilde {\mathcal {A}} \models \tilde {\varphi }_0 \land \neg \tilde {\varphi }_1$
and
![]() $\tilde {\mathcal {A}}^{\star } \models \neg \tilde {\varphi }_0 \land \tilde {\varphi }_1$
. But this contradicts Lemma 5.5.
$\tilde {\mathcal {A}}^{\star } \models \neg \tilde {\varphi }_0 \land \tilde {\varphi }_1$
. But this contradicts Lemma 5.5.
Funding
The work of the first author is supported by the Mathematical Center in Akademgorodok under the agreement No. 075-15-2022-282 with the Ministry of Science and Higher Education of the Russian Federation. The work of the third author was supported by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement No. 101026834 — ACOSE. This project received support from the Austrian Agency for International Cooperation in Education and Research under grant WTZ-BG11/2019 and from the Bulgarian National Science Fund through contracts KP-06-Austria-04/06.08.2019. The fourth and fifth authors were also partially supported by Sofia University Science Fund, project 80-10-134/20.05.2022.