1 results
Contributions to a General Theory of View-Obstruction Problems
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 3 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 517-536
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation
-
In the original view-obstruction problem congruent closed, centrally symmetric convex bodies centred at the points of the set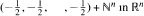
are expanded uniformly until they block all rays from the origin into the open positive cone. The central problem is to determine the minimal blocking size and this value is known for balls in dimensions n = 2,3 and for symmetrically placed cubes in dimensions n = 2, 3, 4In order to explain fully the distinction between rational and irrational rays in the original problem, we extend consideration to the blocking of subspaces of all dimensions. In order to appreciate the special properties of balls and cubes, we give a discussion of the convex body with respect to reflection symmetry, lower dimensional sections, and duality. We introduce topological considerations to help understand when the critical parameter of the theory is an attained maximum and we add substantially to the list of known values of this parameter. In particular, when the dimension is n = 2 our dual body considerations furnish a complete solution to the view-obstruction problem
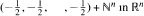are expanded uniformly until they block all rays from the origin into the open positive cone. The central problem is to determine the minimal blocking size and this value is known for balls in dimensions 