9 results
5 - Introduction to Stochastic Processes
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 94-125
-
- Chapter
- Export citation
Joint temporal and contemporaneous aggregation of random-coefficient AR(1) processes with infinite variance
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 237-265
- Print publication:
- March 2020
-
- Article
- Export citation
Statistical Significance and Stability of the Hog Cycle
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 18 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 05 September 2016, pp. 227-234
-
- Article
- Export citation
Estimation in autoregressive model with measurementerror
-
- Journal:
- ESAIM: Probability and Statistics / Volume 18 / 2014
- Published online by Cambridge University Press:
- 03 October 2014, pp. 277-307
- Print publication:
- 2014
-
- Article
- Export citation
A BIVARIATE AUTOREGRESSIVE PROBIT MODEL: BUSINESS CYCLE LINKAGES AND TRANSMISSION OF RECESSION PROBABILITIES
-
- Journal:
- Macroeconomic Dynamics / Volume 18 / Issue 4 / June 2014
- Published online by Cambridge University Press:
- 18 March 2013, pp. 838-862
-
- Article
- Export citation
The Multivariate Ginar(p) Process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 228-248
- Print publication:
- March 1997
-
- Article
- Export citation
A thermal energy storage process with controlled input
-
- Journal:
- Advances in Applied Probability / Volume 14 / Issue 2 / June 1982
- Published online by Cambridge University Press:
- 01 July 2016, pp. 257-271
- Print publication:
- June 1982
-
- Article
- Export citation
Non-linear threshold autoregressive models for non-linear random vibrations
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 2 / June 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 443-451
- Print publication:
- June 1981
-
- Article
- Export citation
Maximum likelihood estimates of incorrect Markov models for time series and the derivation of AIC
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 1 / March 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 59-72
- Print publication:
- March 1980
-
- Article
- Export citation


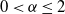
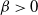
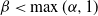

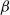
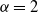
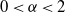
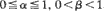 , 0<
, 0<