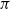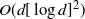1 results
Skew brownian motion and complexity of the alps algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 777-796
- Print publication:
- September 2022
-
- Article
- Export citation
-
Simulated tempering is a popular method of allowing Markov chain Monte Carlo algorithms to move between modes of a multimodal target density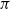
$\pi$
. Tawn, Moores and Roberts (2021) introduces the Annealed Leap-Point Sampler (ALPS) to allow for rapid movement between modes. In this paper we prove that, under appropriate assumptions, a suitably scaled version of the ALPS algorithm converges weakly to skew Brownian motion. Our results show that, under appropriate assumptions, the ALPS algorithm mixes in time 
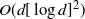$O(d [\log d]^2)$
or O(d), depending on which version is used.
