Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T08:33:33.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Skew brownian motion and complexity of the alps algorithm

Part of: Markov processes

Published online by Cambridge University Press:  12 July 2022

Gareth O. Roberts ,
Jeffrey S. Rosenthal Open the ORCID record for Jeffrey S. Rosenthal [Opens in a new window]  and
Nicholas G. Tawn
Gareth O. Roberts*
Affiliation:
University of Warwick
Jeffrey S. Rosenthal*
Affiliation:
University of Warwick
Nicholas G. Tawn*
Affiliation:
University of Warwick
*
*Postal address: Department of Statistics, University of Warwick, United Kingdom, CV4 7AL.
***Postal address: Department of Statistical Sciences, University of Toronto, 100 St. George Street, Room 6018, Toronto, Ontario, Canada M5S 3G3. Email: [email protected]
*Postal address: Department of Statistics, University of Warwick, United Kingdom, CV4 7AL.
Get access Rights & Permissions [Opens in a new window]

Abstract

Simulated tempering is a popular method of allowing Markov chain Monte Carlo algorithms to move between modes of a multimodal target density 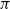$\pi$ . Tawn, Moores and Roberts (2021) introduces the Annealed Leap-Point Sampler (ALPS) to allow for rapid movement between modes. In this paper we prove that, under appropriate assumptions, a suitably scaled version of the ALPS algorithm converges weakly to skew Brownian motion. Our results show that, under appropriate assumptions, the ALPS algorithm mixes in time $O(d [\log d]^2)$ or O(d), depending on which version is used.

Keywords

Markov chain Monte CarloALPS algorithmskew Brownian motiongeneratordiffusion limit

MSC classification

Primary: 60J25: Continuous-time Markov processes on general state spaces
Secondary: 60J05: Discrete-time Markov processes on general state spaces 60J22: Computational methods in Markov chains
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 3 , September 2022 , pp. 777 - 796
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aarts, E. and Korst, J. (1988). Simulated Annealing and Boltzmann Machines. John Wiley, New York.Google Scholar
Atchadé, Y. F., Roberts, G. O. and Rosenthal, J. S. (2011). Towards optimal scaling of Metropolis-coupled Markov chain Monte Carlo. Statist. Comput. 21, 555–568.10.1007/s11222-010-9192-1CrossRefGoogle Scholar
Barlow, M. T., Pitman, J. and Yor, M. (1989). On Walsh’s Brownian motions. In Séminaire de Probabilités XXIII, eds J. Azéma, M. Yor and P. A. Meyer. Springer, New York, pp. 275–293.10.1007/BFb0083979CrossRefGoogle Scholar
Bédard, M. and Rosenthal, J. S. (2008). Optimal scaling of Metropolis algorithms: Heading toward general target distributions. Canad. J. Statist. 36, 483–503.10.1002/cjs.5550360401CrossRefGoogle Scholar
Beskos, A., Pillai, N., Roberts, G., Sanz-Serna, J.-M. and Stuart, A. (2013). Optimal tuning of the hybrid Monte Carlo algorithm. Bernoulli, 19, 1501–1534.10.3150/12-BEJ414CrossRefGoogle Scholar
Brooks, S., Gelman, A., Jones, G. L. and Meng, X.-L. (eds) (2011). Handbook of Markov Chain Monte Carlo. Chapman & Hall, London.10.1201/b10905CrossRefGoogle Scholar
Ethier, S. N. and Kurtz, T. G. (1986). Markov Processes: Characterization and Convergence. John Wiley, New York.10.1002/9780470316658CrossRefGoogle Scholar
Freidlin, M. and Weber, M. (2001). On random perturbations of Hamiltonian systems with many degrees of freedom. Stoch. Proc. Appl. 94, 199–239.10.1016/S0304-4149(01)00083-7CrossRefGoogle Scholar
Geyer, C. J. (1991). Markov chain Monte Carlo maximum likelihood. Comput. Sci. Statist. 23, 156–163.Google Scholar
Hastings, W. K. (1970). Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109.10.1093/biomet/57.1.97CrossRefGoogle Scholar
Jacka, S. and Hernández-Hernández, Ma. E. (2019). Minimising the expected commute time. Stoch. Proc. Appl., DOI 10.1016/j.spa.2019.04.010.Google Scholar
Kirkpatrick, S., Gelatt, C. D. and Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220, 671–680.10.1126/science.220.4598.671CrossRefGoogle ScholarPubMed
Kone, A. and Kofke, D. A. (2005). Selection of temperature intervals for parallel-tempering simulations. J. Chem. Phys. 122, 206101.10.1063/1.1917749CrossRefGoogle ScholarPubMed
Lejay, A. (2006). On the constructions of the skew Brownian motion. Prob. Surv. 3, 413–466.10.1214/154957807000000013CrossRefGoogle Scholar
Liggett, T. M. (2010). Continuous Time Markov Processes: An Introduction. American Mathematical Society, Providence, RI.10.1090/gsm/113CrossRefGoogle Scholar
Marinari, E. and Parisi, G. (1992). Simulated tempering: A new Monte Carlo scheme. Europhys. Lett. 19, 451.10.1209/0295-5075/19/6/002CrossRefGoogle Scholar
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. and Teller, E. (1953). Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092.10.1063/1.1699114CrossRefGoogle Scholar
Pincus, M. (1970). A Monte Carlo method for the approximate solution of certain types of constrained optimization problems. J. Operat. Res. Soc. Amer. 18, 967–1235.Google Scholar
Predescu, C., Predescu, M. and Ciobanu, C. V. (2004). The incomplete beta function law for parallel tempering sampling of classical canonical systems. J. Chem. Phys. 120, 4119–4128.10.1063/1.1644093CrossRefGoogle ScholarPubMed
Revuz, D. and Yor, M. (2004). Continuous Martingales and Brownian Motion, 3rd edn. Springer, New York.Google Scholar
Roberts, G. O., Gelman, A. and Gilks, W. R. (1997). Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Prob. 7, 110–120.Google Scholar
Roberts, G. O. and Rosenthal, J. S. (1998). Optimal scaling of discrete approximations to Langevin diffusions. J. R. Statist. Soc. B 60, 255–268.10.1111/1467-9868.00123CrossRefGoogle Scholar
Roberts, G. O. and Rosenthal, J. S. (2001). Optimal scaling for various Metropolis–Hastings algorithms. Statist. Sci. 16, 351–367.10.1214/ss/1015346320CrossRefGoogle Scholar
Roberts, G. O. and Rosenthal, J. S. (2014). Complexity bounds for Markov chain Monte Carlo algorithms via diffusion limits. J. Appl. Prob. 24, 1–11.Google Scholar
Roberts, G. O. and Rosenthal, J. S. (2014). Minimising MCMC variance via diffusion limits, with an application to simulated tempering. Ann. Appl. Prob. 24, 131–149.10.1214/12-AAP918CrossRefGoogle Scholar
Rosenthal, J. S. (2002). Quantitative convergence rates of Markov chains: A simple account. Electron. Commun. Prob. 7, 123–128.10.1214/ECP.v7-1054CrossRefGoogle Scholar
Rosenthal, J. S. (2020). Maximum binomial probabilities and game theory voter models. Adv. Appl. Statist., 64, 75–85.Google Scholar
Syed, S., Bouchard-Côté, A., Deligiannidis, G. and Doucet, A. (2020). Non-reversible parallel tempering: A scalable highly parallel MCMC scheme. Preprint, arXiv:1905.02939.Google Scholar
Tawn, N. G., Moores, M. T. and Roberts, G. O. (2021). Annealed Leap-Point Sampler for multimodal target distributions. Preprint, arXiv:2112.12908.Google Scholar
Tawn, N. G. and Roberts, G. O. (2018). Accelerating parallel tempering: Quantile Tempering Algorithm (QuanTA). Adv. Appl. Prob. 51, 802–834.10.1017/apr.2019.35CrossRefGoogle Scholar
Tawn, N. G., Roberts, G. O. and Rosenthal, J. S. (2020). Weight-preserving simulated tempering. Statist. Comput. 30, 27–41.10.1007/s11222-019-09863-3CrossRefGoogle Scholar
Woodard, D. B., Schmidler, S. C. and Huber, M. (2009). Sufficient conditions for torpid mixing of parallel and simulated tempering. Electron. J. Prob. 14, 780–804.10.1214/EJP.v14-638CrossRefGoogle Scholar