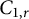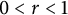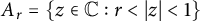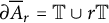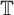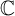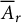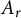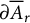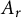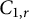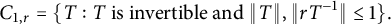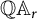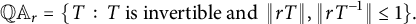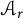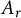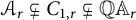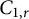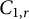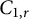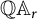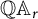For fixed 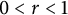 $0<r<1$, let
$0<r<1$, let 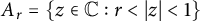 $A_r=\{z \in \mathbb {C} : r<|z|<1\}$ be the annulus with boundary
$A_r=\{z \in \mathbb {C} : r<|z|<1\}$ be the annulus with boundary 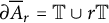 $\partial \overline {A}_r=\mathbb {T} \cup r\mathbb {T}$, where
$\partial \overline {A}_r=\mathbb {T} \cup r\mathbb {T}$, where 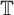 $\mathbb T$ is the unit circle in the complex plane
$\mathbb T$ is the unit circle in the complex plane 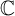 $\mathbb C$. An operator having
$\mathbb C$. An operator having 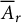 $\overline {A}_r$ as a spectral set is called an
$\overline {A}_r$ as a spectral set is called an 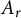 $A_r$-contraction. Also, a normal operator with its spectrum lying in the boundary
$A_r$-contraction. Also, a normal operator with its spectrum lying in the boundary 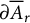 $\partial \overline {A}_r$ is called an
$\partial \overline {A}_r$ is called an 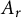 $A_r$-unitary. The
$A_r$-unitary. The 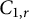 $C_{1,r}$ class was introduced by Bello and Yakubovich in the following way:
$C_{1,r}$ class was introduced by Bello and Yakubovich in the following way: 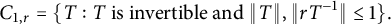 $$\begin{align*}C_{1, r}=\{T: T \ \text{is invertible and} \ \|T\|, \|rT^{-1}\| \leq 1\}. \end{align*}$$
$$\begin{align*}C_{1, r}=\{T: T \ \text{is invertible and} \ \|T\|, \|rT^{-1}\| \leq 1\}. \end{align*}$$
McCullough and Pascoe defined the quantum annulus 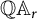 $\mathbb Q \mathbb A_r$ by
$\mathbb Q \mathbb A_r$ by 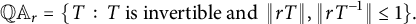 $$\begin{align*}\mathbb Q\mathbb A_r = \{T \,:\, T \text{ is invertible and } \, \|rT\|, \|rT^{-1}\| \leq 1 \}. \end{align*}$$
$$\begin{align*}\mathbb Q\mathbb A_r = \{T \,:\, T \text{ is invertible and } \, \|rT\|, \|rT^{-1}\| \leq 1 \}. \end{align*}$$
If 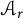 $\mathcal A_r$ denotes the set of all
$\mathcal A_r$ denotes the set of all 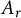 $A_r$-contractions, then
$A_r$-contractions, then 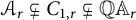 $\mathcal A_r \subsetneq C_{1,r} \subsetneq \mathbb Q \mathbb A_r$. We first find a model for an operator in
$\mathcal A_r \subsetneq C_{1,r} \subsetneq \mathbb Q \mathbb A_r$. We first find a model for an operator in 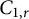 $C_{1,r}$ and also characterize the operators in
$C_{1,r}$ and also characterize the operators in 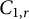 $C_{1,r}$ in several different ways. We prove that the classes
$C_{1,r}$ in several different ways. We prove that the classes 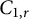 $C_{1,r}$ and
$C_{1,r}$ and 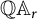 $\mathbb Q\mathbb A_r$ are equivalent. Then, via this equivalence, we obtain analogous model and characterizations for an operator in
$\mathbb Q\mathbb A_r$ are equivalent. Then, via this equivalence, we obtain analogous model and characterizations for an operator in 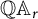 $\mathbb Q \mathbb A_r$.
$\mathbb Q \mathbb A_r$.
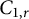 $C_{1,r}$ class and quantum annulus
$C_{1,r}$ class and quantum annulus