No CrossRef data available.
Article contents
Characterizations and models for the 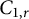 $C_{1,r}$ class and quantum annulus
$C_{1,r}$ class and quantum annulus
Published online by Cambridge University Press: 07 February 2025
Abstract
For fixed 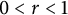 $0<r<1$, let
$0<r<1$, let 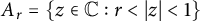 $A_r=\{z \in \mathbb {C} : r<|z|<1\}$ be the annulus with boundary
$A_r=\{z \in \mathbb {C} : r<|z|<1\}$ be the annulus with boundary 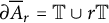 $\partial \overline {A}_r=\mathbb {T} \cup r\mathbb {T}$, where
$\partial \overline {A}_r=\mathbb {T} \cup r\mathbb {T}$, where 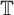 $\mathbb T$ is the unit circle in the complex plane
$\mathbb T$ is the unit circle in the complex plane 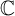 $\mathbb C$. An operator having
$\mathbb C$. An operator having 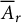 $\overline {A}_r$ as a spectral set is called an
$\overline {A}_r$ as a spectral set is called an 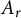 $A_r$-contraction. Also, a normal operator with its spectrum lying in the boundary
$A_r$-contraction. Also, a normal operator with its spectrum lying in the boundary 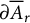 $\partial \overline {A}_r$ is called an
$\partial \overline {A}_r$ is called an 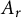 $A_r$-unitary. The
$A_r$-unitary. The 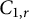 $C_{1,r}$ class was introduced by Bello and Yakubovich in the following way:
$C_{1,r}$ class was introduced by Bello and Yakubovich in the following way: 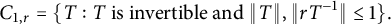 $$\begin{align*}C_{1, r}=\{T: T \ \text{is invertible and} \ \|T\|, \|rT^{-1}\| \leq 1\}. \end{align*}$$
$$\begin{align*}C_{1, r}=\{T: T \ \text{is invertible and} \ \|T\|, \|rT^{-1}\| \leq 1\}. \end{align*}$$
McCullough and Pascoe defined the quantum annulus 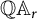 $\mathbb Q \mathbb A_r$ by
$\mathbb Q \mathbb A_r$ by 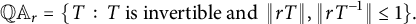 $$\begin{align*}\mathbb Q\mathbb A_r = \{T \,:\, T \text{ is invertible and } \, \|rT\|, \|rT^{-1}\| \leq 1 \}. \end{align*}$$
$$\begin{align*}\mathbb Q\mathbb A_r = \{T \,:\, T \text{ is invertible and } \, \|rT\|, \|rT^{-1}\| \leq 1 \}. \end{align*}$$
If 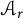 $\mathcal A_r$ denotes the set of all
$\mathcal A_r$ denotes the set of all 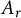 $A_r$-contractions, then
$A_r$-contractions, then 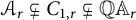 $\mathcal A_r \subsetneq C_{1,r} \subsetneq \mathbb Q \mathbb A_r$. We first find a model for an operator in
$\mathcal A_r \subsetneq C_{1,r} \subsetneq \mathbb Q \mathbb A_r$. We first find a model for an operator in 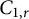 $C_{1,r}$ and also characterize the operators in
$C_{1,r}$ and also characterize the operators in 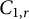 $C_{1,r}$ in several different ways. We prove that the classes
$C_{1,r}$ in several different ways. We prove that the classes 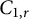 $C_{1,r}$ and
$C_{1,r}$ and 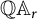 $\mathbb Q\mathbb A_r$ are equivalent. Then, via this equivalence, we obtain analogous model and characterizations for an operator in
$\mathbb Q\mathbb A_r$ are equivalent. Then, via this equivalence, we obtain analogous model and characterizations for an operator in 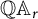 $\mathbb Q \mathbb A_r$.
$\mathbb Q \mathbb A_r$.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
The first named author is supported by the Seed Grant of IIT Bombay, the CDPA and the “Core Research Grant” with Award No. CRG/2023/005223 of Science and Engineering Research Board (SERB), India. The second named author is supported by the Prime Minister’s Research Fellowship (PMRF ID 1300140), Government of India.



